带耦合时滞的复杂网络通过时滞脉冲牵制控制达到同步

张 兰

(重庆师范大学 数学科学学院，重庆 401331)



带耦合时滞的复杂网络通过时滞脉冲牵制控制达到同步

张 兰

(重庆师范大学 数学科学学院，重庆 401331)

研究了带有耦合时滞的复杂网络通过时滞脉冲牵制控制达到同步的问题，其中时滞脉冲牵制控制被设计，基于李雅普诺夫函数法等，提出了保证复杂动力网络的指数同步的一些充分条件.本文的结果是基于先前结果的促进和改善.最后，通过数值模拟证明了结果的有效性.

复杂动力系统；指数同步；时滞脉冲牵制控制；耦合时滞

在过去的20年里，复杂动力网络的研究在现代社会中各个领域发挥的作用越来越重要，可以发现在安全通信、生物系统、信息处理等各个领域都得到广泛应用，因此引起了广大学者的关注.而其中复杂网络的同步问题各个学者研究的重要现象之一[1-2]，它的意思是指两个或两个以上随时间变化的量在变化过程中保持一定的相对关系，同步又包括完全同步[3]、拟同步[4]、广义同步[5]等.现在许多研究人员通过各种控制方法使系统达到同步，常见的控制方法包括间歇控制[6]、反馈控制[7]、自适应控制[8]、脉冲控制[9]等等，但是各种控制都是有利也有弊.

在这之前，许多研究者通过反馈控制使得系统达到同步[7]，但是反馈控制的保守性比较高，不能很好地应用于实际生活中.然而脉冲控制方法比较易于应用到实际生活中，因为它只需要小的控制增益和控制行为只在离散的时间施加，从而控制成本和传播信息的数量会大大降低.本文研究通过脉冲时滞牵制控制复杂网络达到同步的原因，其一是因为时滞在通信的传输过程中必然会发生，但是在以往的文章中，研究者只在系统中考虑了时滞[10]，没有在控制中考虑.其二是因为为了降低成本.基于以上原因本文设计了牵制控制，即只通过控制系统的部分节点，再通过系统的耦合性从而达到控制整个系统达到同步的目的，这样控制方法进一步降低了成本和传播信息的数量.基于以上原因，本文存在较大的研究意义.

1 基本定义与预备知识

考虑以下带耦合时滞的复杂网络动力系统：

(1)

其中N为系统的节点数，xi(t)=(xi1(t),xi2(t),…,xin(t))T∈n是第i个节点的状态变量，f(x)=(f1(x1(t)),f2(x2(t)),…,fn(xn(t)))T∈n和h(x(t-τ(t)))=(h1(x1(t-τ(t))),h2(x2(t-τ(t))),…,hn(xn(t-τ(t))))T是激活函数；τ(t)是耦合变时滞，并且满足0≤τ(t)≤τ，其中τ为正数.A∈n×n是已知的常数矩阵，Γ∈n×n表示内部耦合矩阵，B=(bij)n×n是时滞耦合矩阵，并且满足耦合条件：如果节点i与j有联系(i≠j)，那么aij≠0；否则aij=0,其中当i=j时，.

然后使用Kronecker，那么系统(1)可以写成如下形式：

(2)

系统(2)的初值为：

xi(s)=φi(s),-τ≤s≤0,i=1,2,…,N.

以下为同步状态方程：

(3)

它的初始条件可以描述为：s(t)=ψi(t),-τ≤t≤0,i=1,2,…,N.

(4)

设e(t)=x(t)-s(t)，系统(4)与系统(3)作差可以得到误差系统如下：

(5)

在设计出能使系统达到同步的控制之前，需要做以下的假设：

(H1) 存在正整数kij,gij,i,j=1,2,…,N,使得f,h满足以下不等式：

(6)

(7)

下面给出全局指数同步的定义.

定义1 设V:R+×Rn→R+:如果存在正整数M>1,k>0，对于任何初值都使得:

成立，那么系统(3)在控制下与系统(2)达到全局指数同步.

下面给出一些本文需要的引理.

引理 1[11]下面不等式恒成立：

(8)

证明： 因为:

(9)

(10)

(11)

由于N>l:

(12)

同理可得:

(13)

引理 2[12]假设ρ>0，对于任意x,y∈n，下面不等式都成立：y.

引理 3[3]考虑以下的微分不等式：

(14)

假设:

(15)

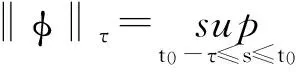
2 主要结果

在本节中，脉冲时滞牵制控制被设计，通过脉冲时滞牵制控制器，系统(3)与系统(2)能够达到同步，并得到了同步的标准.

定理 1 假设条件(H1)成立，并且存在ρ1>0,ρ2>0使得下列不等式成立:

(16)

(17)

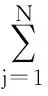
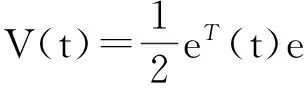
当t≠tk时，

(18)

一方面，根据(H1)和引理2，存在正常数ρ1使得：

(19)

另一方面，存在正常数ρ2，与上面的方法相似，可以得到：

令G=(gij)N×N,

(20)

将不等式(19)和不等式(20)代入不等式(18)，可以得到：

(21)

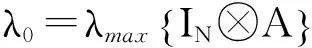
(22)

根据Lyapunov的构造得：

(23)

当t=tk时，对脉冲部分进行分析：

(24)

根据引理2，不等式变成如下：

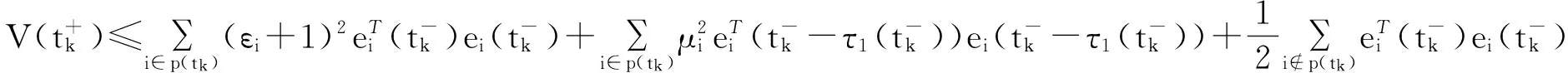
(25)

(26)

其中p(tk)表示发生脉冲的节点集合，再根据引理1得：

(27)

基于引理3，从式(16)，(17)，(23)和(27)推导中可以得到存在正常数M>1，k>0使得:

将h(x(t-τ(t)))变成简单的x(t-τ)，可以得到下面的推论.

推论1 假设条件(H1)成立，并且存在ρ1>0，ρ2>0使得下列不等式成立:

(28)

(29)

3 应用

本节通过一些实际例子证明了结果的有效性.

例1 当n=3,N=5时，带非线性有界干扰的复杂动力网络被描述为如下的形式：

(30)

其中x(t)=(x1(t),x2(t),x3(t))T,τ=1,

系统的内部耦合矩阵为：

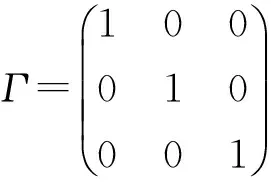
其中脉冲的发生间隔tk+1-tk=0.01，并且通过计算可以得到：

通过上面的分析可以得到：

dk=0.58<1,

根据引理3可以得出结论，系统(30)能够达到同步状态，从而证明了结果的有效性.

[1]YANGX,CAOJ.Hybridadaptiveandimpulsivesynchronizationofuncertaincomplexnetworkswithdelaysandgeneraluncertainperturbations[J].AppliedMathematicsandComputation，2014,227：480-493.

[2] YANG X,CAO J, YANG A.Synchronization of coupled reaction-diffusion neural networks with time-varying delays via pinning-impulsive controller[J].SIAM J CONTROL OPTIM,2015,51(5):3486-3510.

[3] YANG A,YANG Z.Synchronization of TS fuzzy complex dynamical networks with time-varying impulsive delays and stochastic effects[J].Fuzzy Set and Systems,2014,235:25-43.

[4] LIU X,CHEN T,CAO J,et al.Dissipativity and quasi-synchronization for neural networks with discontinuous activations and parameter mismatches[J].Neural Networks,2011,24:1013-1021.

[5] WU E,YANG X.Generalized lag synchronization of neural networks with discontinuous activations and bounded perturbations[J].Circuits Systems Signal Process,DOI 10.1007/s00034-014-9962-7.

[6] YANG X,CAO J.Stochastic synchronization of coupled neural networks with intermittent control[J].Physics Letters A,2009,373(36):3259-3272.

[7] BATISTA CAS,LOPES SR,VIANA RL,et al.Delayed feedback control of bursting synchronization in a scale-free neuronal network[J].Neural Network,2010,23(1):114-124.

[8] ZHOU J,LU J,LU J.Pinning adaptive synchronization of a general complex dynamical network[J].Automatica,2008,44(4):996-1003.

[9] YANG X,HUANG C,YANG Z.Stochastic synchronization of reaction-diffusion neural networksunder general impulsive controller with mixed delays[J].Abst Appl Anal,2012,2012:1-25.Art. ID.603535.

[10] GUAN Z,LIU Z,FENG G,et al.Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control[J].IEEE Trans Circuits System,2010,57(8):2182-2195.

[11] WU Z,CHEN G,Fu Xinchu.Out synchronization of drive-response dynamical networks via adaptive impulsive pinning control[J].Journal of the Franklin institute,2015,352:4297-4308.

[12] WANG T,XIE L,de Souza CE.Robust control of a class of uncertain nonlinear systems[J].Systems Control Letters,1992,19(2):139-149.

责任编辑：时 凌

Exponential Synchronization of Complex Dynamical Networks with Coupling Time-delay via Time-delayed Impulsive Pinning Control

ZHANG Lan

(Department of Mathematics,Chongqing Normal University,Chongqing 401331,China)

Exponential synchronization of complex dynamical networks with coupling time-delay via time-delayed impulsive pinning control is studied.Time-delayed impulsive pinning control is designed.Based on Lyapunov function method,etc.Some sufficient conditions are proposed to guarantee the exponential syn-chronization of complex dynamical networks. The results of this paper is based on the previous results made to promote and improve.Finally,numerical simulations are given to show the effectiveness of the theoretical results.

complex dynamical networks;exponential synchronization;time-delayed impulsive pinning contorl;coupling time-delay

2016-07-26.

国家自然科学基金项目(61263020).

张兰(1993- )，女，硕士生，主要从事控制论的研究.

1008-8423(2016)03-0276-06

10.13501/j.cnki.42-1569/n.2016.09.008

O189.1

A