基于反向学习机制的蝙蝠算法

岳伟娜，马吉明，苏日建，郭盛楠

(郑州轻工业学院 计算机与通信工程学院，河南 郑州 450002)



基于反向学习机制的蝙蝠算法

岳伟娜，马吉明，苏日建，郭盛楠

(郑州轻工业学院 计算机与通信工程学院，河南 郑州 450002)

针对蝙蝠算法存在收敛速度慢，寻优精度低问题，提出一种基于反向学习的蝙蝠算法，该算法具有易跳出局部最优，寻优精度高，种群多样性且鲁棒性好等特点.通过对6个典型的测试函数进行仿真实验，结果表明该算法是行之有效的，且在求解多峰函数时运算的效果更好.

蝙蝠算法;反向学习;多样性;鲁棒性

蝙蝠算法(BA) 是Yang教授[1]于2010年基于群体智能提出的启发式搜索算法,是一种搜索全局最优解的有效方法.蝙蝠算法模拟的是微型蝙蝠的回声定位原理，该算法利用频率调谐技术来提高种群中解的多样性,通过自动缩放技术来改变脉冲发射速率和脉冲响度的大小来平衡算法搜索过程中全局寻优和局部寻优的平衡性.与遗传算法相比，蝙蝠算法简单、容易实现同时又有深刻的智能背景，既适合科学研究，又特别适合工程应用.如多目标优化、工程优化、大规模优化等问题.但蝙蝠算法的缺点有易陷入局部极值点，进化后期收敛慢，精度较差等.严重的制约了蝙蝠算法的应用领域.为了克服蝙蝠优化算法的缺点，目前出现了大量的改进蝙蝠算法，本文引入反向学习机制，该算法在收敛速度和计算精度方面相比蝙蝠算法有所提高，可以选出部分优秀的反向个体加入到全局搜索，这样既增加了种群多样性，又让粒子更容易使算法跳出局部极值的限制.这种改进在一定程度上解决了基本BA算法的收敛速度、算法等缺点.并通过对6个典型的测试函数进行仿真实验，结果表明该算法是行之有效的，且在求解多峰函数时运算的效果更好.

1 相关知识

1.1 原始蝙蝠算法

蝙蝠拥有回声定位能力，它们能产生短促而频率高的声波脉冲，这些声波在碰到附近物体便反射回来[2-4].然后这些反射回来的声波被蝙蝠大耳廓所接收，声波反馈的信息被它们微细的大脑所分析，为飞行提供导向.所以蝙蝠利用回声定位的方法感知距离,并且它们采用一种巧妙的方式来区别猎物和背景障碍物之间的不同.

在理想状态下，蝙蝠算法[5-7]是利用蝙蝠在觅食时所发出的脉冲的频率、响度、脉冲发射率的变化而模拟设计出的群智能算法.基本蝙蝠算法是模拟蝙蝠的觅食行为，通过频率f的调整引起波长λ的变化(λf=v).其中，v是声波在空气中的传播速度，频率f在[fmin,fmax]范围内变化．蝙蝠按脉冲发射率ri在[0，1]的范围内和响度Ai发出声波脉冲来近似无声无息[8]的搜索猎物.

BA算法和其他进化算法相比有很多相似之处，都能用来求解方程的优化问题.比如多元函数的优化问题[9-10].而大量的理论和实验研究结果表明，BA算法在解决一些典型实际的优化问题时，相比较其他算法能够取得较好的优化结果.BA算法被成功地应用于多目标优化，自动目标检测和决策调度等领域并且取得了良好的效果.

如上所述，蝙蝠算法包含搜索脉冲频率、速度和位置更新、脉冲音强及脉冲发射频度四个要素.

搜索脉冲频率方程为：

(1)

其中：a为[0,1]范围内的随机数，fi，fmax，fmin分别指当前脉冲频率，频率最大值和最小值.

飞行速度方程为：

(2)

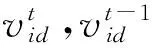
位置更新方程为：

(3)

随机游走方程为：

(4)

脉冲响应强度方程为：

(5)

其中：β，γ为常数，脉冲发射频度方程为：

(6)

1.2 反向学习机制

近年来，反向学习是多种优化算法应用中的一种新技术，首先需要对所有粒子的位置求出其适应值，得到适应最大值xmax和适应最小值xmin，然后，对所有粒子进行式(7)的运算得出新的粒子位置并求出所有粒子的适应值，对新得到的适应最小值与之前的适应最小值进行比较，若前者小于后者，则对前者的位置信息进行更新.反向学习[11-15]机制的方程为：

(7)

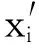
2 改进的蝙蝠算法

从蝙蝠算法的步骤可以看出，在迭代过程中，整个群体只向最优的个体学习，一旦发现最优个体，则所有粒子都往该处寻找，这种位置更新方式不仅大幅降低了粒子种群的多样性，并且如果该位置并不是全局最优，则也有可能导致算法陷入局部最优，进而对收敛精度和收敛速度有一定影响.事实上，蝙蝠种群在整个搜索空间中，全局最优往往存在于局部最优的附近，并且种群的进化速度更大程度取决于较差个体而不是较优个体.

本文在蝙蝠算法的基础上，引入了反向学习机制来调节粒子的运动轨迹，这样不仅有助于增加萤火虫群体的多样性和跳出局部最优，且当粒子在全局最优附近时具有较好的收敛性.其主要作用在于当粒子在进行搜索时，在本种群及其反向种群中寻找最优个体作为当前的全局最优，这样不仅有助于跳出局部最优，且当粒子在全局最优附近时得到较好的收敛性.

具有反向学习机制的BA算法(OL-BA)的具体步骤如下：

1)初始化种群，在定义域内随机生成蝙蝠种群大小为n，设定收索空间维数为m，设定每个蝙蝠个体的初识位置，速度，响应和脉冲发射率.

2)根据适应度函数去确定蝙蝠群体中的最优个体；

3)根据式(7)对种群进行反向学习并代入适应度函数进行计算；

4)反向学习前后计算出的适应度值进行比较，取值较好的个体代替并加入种群中；

5)根据式(1)去设定每个蝙蝠个体的频率；

6)根据式(2)和式(3)去更新每个蝙蝠的速度和位置；

7)计算适应度值，从而更新每个蝙蝠的历史最优和全局最优；

8)对每个蝙蝠进行rand>ri;满足条件按式(4)计算，若新解较好，取代旧解并更新蝙蝠的历史最优和全局最优；

9)根据式(5)和(6)对蝙蝠个体的响度和脉冲发射率进行更新；

10)当迭代次数未达到最大迭代次数，则返回步骤(2)继续往下执行，直到迭代结束，输出结果为止.

表1 标准测试函数

3 仿真实验及分析

实验平台：处理器CPU I5-3470，主频3.20 GHz，内存4 GB，操作系统：Windows XP，集成开发环境MATLAB R2012a.

为了验证OL-BA的算法的性能，分别将BA算法，LF-BA算法和OL-BA算法用于6个典型的测试函数，并在MATLAB软件中对各个算法运行的结果进行了测试和比较，这6个测试函数为：

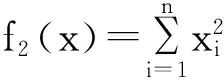
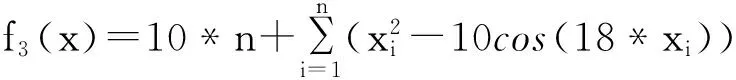
蝙蝠算法中的参数无确切的理论依据，而具反向学习的蝙蝠算法中：个体个体i最大脉冲频度r0=0.75，最大脉冲响度Ai=0.25，脉冲响度衰减系数β =0.9，脉冲频度增加系数 γ=0.05，Lévy飞行尺度参数λ=1.5.对6个不同的测试函数的最大迭代次数和种群数分别设置不同的数值，如表1所示.

在进行最优值和平均最优值分析时，具体参数设定如下：迭代次数为200次，种群规模为40个.为了避免算法的偶然性带来的误差，对6个函数在不同的维度上都独立运行30次，取其中的最差值和最优值及平均值带入到表2中.

表2 测试函数的最优值、最差值和平均最优值

从表2中可以看出，文中提出的算法与BA算法和LF-BA算法相比，在求解低维函数f1时，OL-BA算法的综合优化性能较好；在对多峰值且求解域内有大量的局部最优值的f3到f6时，BA算法得到的最优值和理论的最优值的偏差较大.而OL-BA算法在得到的最优值和理论值较为接近且算法的鲁棒性能较好.特别是在求解f2，BA算法得到的最优值和最差值之间的差值较大得到的平均值离理论值较远，而OL-BA算法在这方面就体现出优势，进一步说明了OL-BA算法具有很好的适应性和鲁棒性.

为了测试OL-BA算法的收敛速度，搜索能力和寻优精度等，一般情况都采用如下方法：在相同的测试函数相同维度下，评估各个算法的搜索能力，寻优能力和鲁棒性.

如图1所示，可以看出在求解低维度的函数时，三个算法在运行到20次左右都可以达到3位数的精度，只是改进算法的收敛速度比原始算法更快些.如图2所示， OL-BA的收敛速度上明显好于BA和LF-BA算法且在25次左右收敛于5位数的精度，如图3至图5所示，在求解多峰函数时，OL-BA和LF-BA两种算法要明显优于原始的BA算法，但OL-BA算法的收敛速度明显好于后者.从图6可以看出，当迭代到100次时，BA算法陷入局部最优值，当迭代到145次左右时，两个改进算法都收敛到3位数精度，由于步长因子的限制，LF-BA算法停止了寻优，OL-BA算法还继续寻优到200次达到4位数精度.

图1 Schaffer函数(维数D=2) 图2 Sphere函数(维数D=10)Fig.1 Schaffer function (dimension D=2) Fig.2 Sphere funilion(dimension D=10)

图3 Rastrigin函数(维数D=10) 图4 Ackley函数(维数D=10)Fig.3 Rastrigin function (dimension D=10) Fig.4 Ackley function (dimension D=10)

图5 Griewank函数(维数D=10) 图6 Salomon函数(维数D=20)Fig.5 Griewank function (dimension D=10) Fig.6 Salomon function (dimension D=20)

5 结论

本文针对BA算法的缺点，容易陷入局部极小的缺陷，且精度差.提出了一种基于反向学习的改进BA算法.此算法在寻优的过程中，根据最优粒子和最差粒子之间的信息，得出一个反向种群，根据其最优粒子和先前的最优粒子作比较，取其中较好的粒子并更新当前粒子的坐标信息，这样即增加了粒子种群的多样性也提高了寻优的收敛速度.仿真结果表明，本算法不仅弥补了BA算法的缺陷，还对多峰函数的求解有更好的寻优效果.从而验证了反向学习机制的蝙蝠算法的有效性和可行性，进而扩展了他的应用领域.但是对于算法参数的优化及其应用仍需深入的研究，如何设置自适应参数，提高蝙蝠算法的自适应性，这也是接下来将要进一步的工作.

[1] BISWAS A,BISWAS B.Swarm Intelligence Techniques and Their Adaptive Nature with Applications[M]// Complex System Modelling and Control Through Intelligent Soft Computations. Springer International Publishing,2015:253-273.

[2] Bahmani-Firouzi B, Azizipanah-Abarghooee R. Optimal sizing of battery energy storage for micro-grid operation management using a new improved bat algorithm[J]. International Journal of Electrical Power & Energy Systems, 2014, 56(3):42-54.

[3] MIRJALILI S,MIRJALILI S M,YANG X S.Binary bat algorithm[J].Neural Computing & Applications,2014,25(3/4):663-681.

[4] GANDOMI A H,YANG X S.Chaotic bat algorithm[J].Journal of Computational Science,2014,5(2):224-232.

[5] 李枝勇,马良,张惠珍.蝙蝠算法收敛性分析[J].数学的实践与认识,2013,43(12):182-190.

[6] 张宇楠,刘付永.一种改进的变步长自适应蝙蝠算法及其应用[J].广西民族大学学报(自然科学版),2013,19(2):51-54，81.

[7] 尹进田,刘云连,刘丽,等.一种高效的混合蝙蝠算法[J].计算机工程与应用,2014,50(7):62-66.

[8] YANG X S,GANDOMI A H.Bat algorithm:a novel approach for global engineering optimization[J].Engineering Computations,2012,29(5):464-483.

[9] TSAI P W,PAN J S,LIAO B Y,et al.Bat Algorithm Inspired Algorithm for Solving Numerical Optimization Problems[J].Applied Mechanics & Materials,2011,148-149(148):134-137.

[10] NAKAMURA R Y M,PEREIRA A M,COSTA K A,et al.BBA:A Binary Bat Algorithm for Feature Selection[C]//Graphics,Patterns and Images (SIBGRAPI),2012 25th SIBGRAPI Conference on,IEEE,2012:291-297.

[11] AHANDANI M A,Alavi-Rad H. Opposition-based learning in the shuffled differential evolution algorithm[J].Soft Computing,2012,16(8):1303-1337.

[12] XU Q,WANG L,WANG N,et al.A review of opposition-based learning from 2005 to 2012[J].Engineering Applications of Artificial Intelligence,2014,29(3):1-12.

[13] WANG H,RAHNAMAYAN S,WU Z.Parallel differential evolution with self-adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems[J].Journal of Parallel & Distributed Computing,2013,73(1):62-73.

[14] 汪慎文,丁立新,谢承旺,等.应用精英反向学习策略的混合差分演化算法[J].武汉大学学报(理学版),2013,59(2):111-116.

[15] 周新宇,吴志健,王晖,等.一种精英反向学习的粒子群优化算法[J].电子学报,2013,41(8):1647-1652.

责任编辑：时 凌

Bat Algorithm Based on Opposition Learning Mechanism

YUE Weina，MA Jiming，SU Rijian，GUO Shengnan

(School of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450002,China)

Aiming at the problem that the firefly algorithm has slow convergence and low precision,an improved Bat algorithm based on opposition learning mechanism is proposed.The proposed algorithm is characterized by high precision and good robustness,and it can effectively jump out the local optimum.6 typical test functions are simulated and the results show that the algorithm is effective and feasible.What′s more,the algorithm also has excellent arithmetic performance in solving an optimization problem with multi-modal function.

bat algorithm；opposition learning；diversity；robustnes

2016-08-11.

国家自然科学基金项目(61374014)；河南省科技攻关项目(132102210056、142102210080).

岳伟娜(1989- )，女，硕士生,主要从事数据库与信息集成、智能信息处理的研究.

1008-8423(2016)03-0251-05

10.13501/j.cnki.42-1569/n.2016.09.003

TP391.9

A