基于统计型积分方程的高斯粗糙面散射计算

韩丹枫 胡俊 聂在平

(电子科技大学电子工程学院,成都 611731)



基于统计型积分方程的高斯粗糙面散射计算

韩丹枫 胡俊 聂在平

(电子科技大学电子工程学院,成都 611731)

基于统计型积分方程方法(Stochastic Integral Equation Method,SIEM)实现了高斯粗糙面的高效散射计算.与传统求解随机粗糙面散射特性的蒙特卡洛法(Monte Carlo Method,MC)相比,该方法采用统计面元格林函数,考虑粗糙面高斯随机分布的场源耦合影响,只需要计算一次矩阵元素和待求未知量,提高了求解粗糙面问题的计算效率.数值结果显示,文中方法与MC吻合,计算效率得到显著提高.

电磁散射;统计型积分方程;高斯粗糙面;蒙特卡洛方法

DOI 10.13443/j.cjors.2015082201

引 言

对于入射波频率很高的散射体,传统上我们认为的光滑表面,此时就不再完全光滑,成为微粗糙面,其电参数特性将随着频率升高或尺寸减小与光滑表面差距越来越大. 传统求解粗糙面问题的方法是蒙特卡洛方法(Monte Carlo Method,MC)[1-2],该方法需要重复计算上百次甚至上千次,来进行统计平均,得到收敛的精确结果,所以求解的效率非常低. 本文引入了一种改进型的积分方程方法——统计型积分方程方法(Stochastic Integral Equation Method,SIEM),该方法是将统计特性转移到积分的核上,使得求解过程只需要一次,即可完成传统的统计特性.

MC也被称为统计模拟方法,是20世纪40年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法. 在随机粗糙面电磁特性研究中,MC重复建模求解上千次,使统计平均结果趋向固定,所以该方法效率很低.

SIEM方法由Zhenhai Zhu和Jacob White于2004年提出[3],该方法是将统计因子转移到积分核格林函数上,即在格林函数上进行统计积分,从而实现统计特性一次性计算完成. 该方法的最大优点就是针对满足高斯分布的粗糙面,不再需要精准的几何模型的建立和上千次的建模求解,故该方法相对于传统方法效率有很大的提高.

在Zhu的基础上,我们将该方法延伸至求解三维散射问题中，得到的结果与传统的MC吻合,并且很大地提高了计算效率.

1 理论推导

SIEM的本质思想是在积分方程的基础上,结合满足粗糙面分布的概率密度函数,对相应的积分方程两边进行求统计,相较于MC的整个几何建模与电磁建模结合的统计平均,SIEM则是将统计特性添加到积分方程的积分核上,从而实现了一次性完成整个统计过程.

由SIEM的统计平均思想[3],对理想导电体表面的电场积分方程[4-5]两边进行统计平均,得到

g(r,r′)>dS′=-t· .

(1)

g(r,r′)>dS′=-t·.

(2)

用Galerkin方法匹配,即选择同样的RWG基函数测试上面方程得到

=>.

(3)

将方程(3)写成矩阵形式,即为

(4)

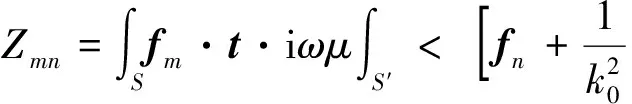
g(r,r′)>dS′dS

fm(r)

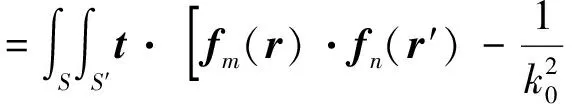
fm(r),

r2)g(r,r′)dh1dh2dS′dS;

Em=-∫Sfm·t·dS

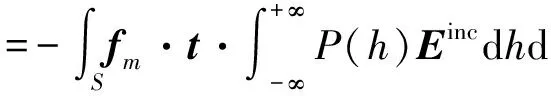
(5)

(6)

式(5)是高斯联合分布,式(6)是一维高斯分布. 其中σ是标准差,表征了粗糙面的起伏高度,C(r1,r2)是相关函数,其定义为

C(r1,r2) =C(|r1-r2|)=C(ξ)

(7)

式(7)中η为相关长度,表征了高斯粗糙面起伏的变化快慢,标准差σ和相关长度η是高斯粗糙面的主要参数[6-7],二者的影响如图1所示.图1是相关长度η=0.5λ,考察均方根变化对粗糙面特性的影响.

由图1(a)和(b)的对比可以看出,图1(b)中粗糙面的粗糙程度比图1(a)中的更大. 图2是均方根σ=0.05λ固定,相关长度η变化对粗糙面特性的影响.

由图1、图2可知,均方根高度影响的是粗糙面的起伏高度,相关长度影响的是粗糙面的变化快慢. 二者公共决定出粗面的特性.

在求解阻抗元素的时候,面元积分用高斯离散积分,统计平均值的计算用Gauss-Hermite积分. 因为Gauss-Hermite积分的统计变量h是沿着面元法向量分布,其积分可以认为是与面元积分相互独立,所以可以改变积分的顺序.

(a) σ=0.05λ

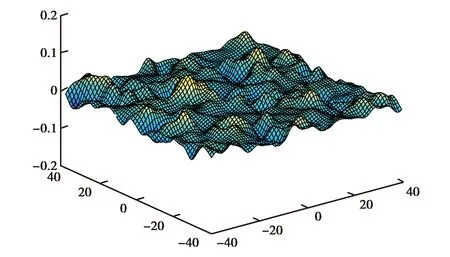
(b) σ=0.1λ图1 均方根σ变化对粗糙面特性的影响

(a) η=0.5λ

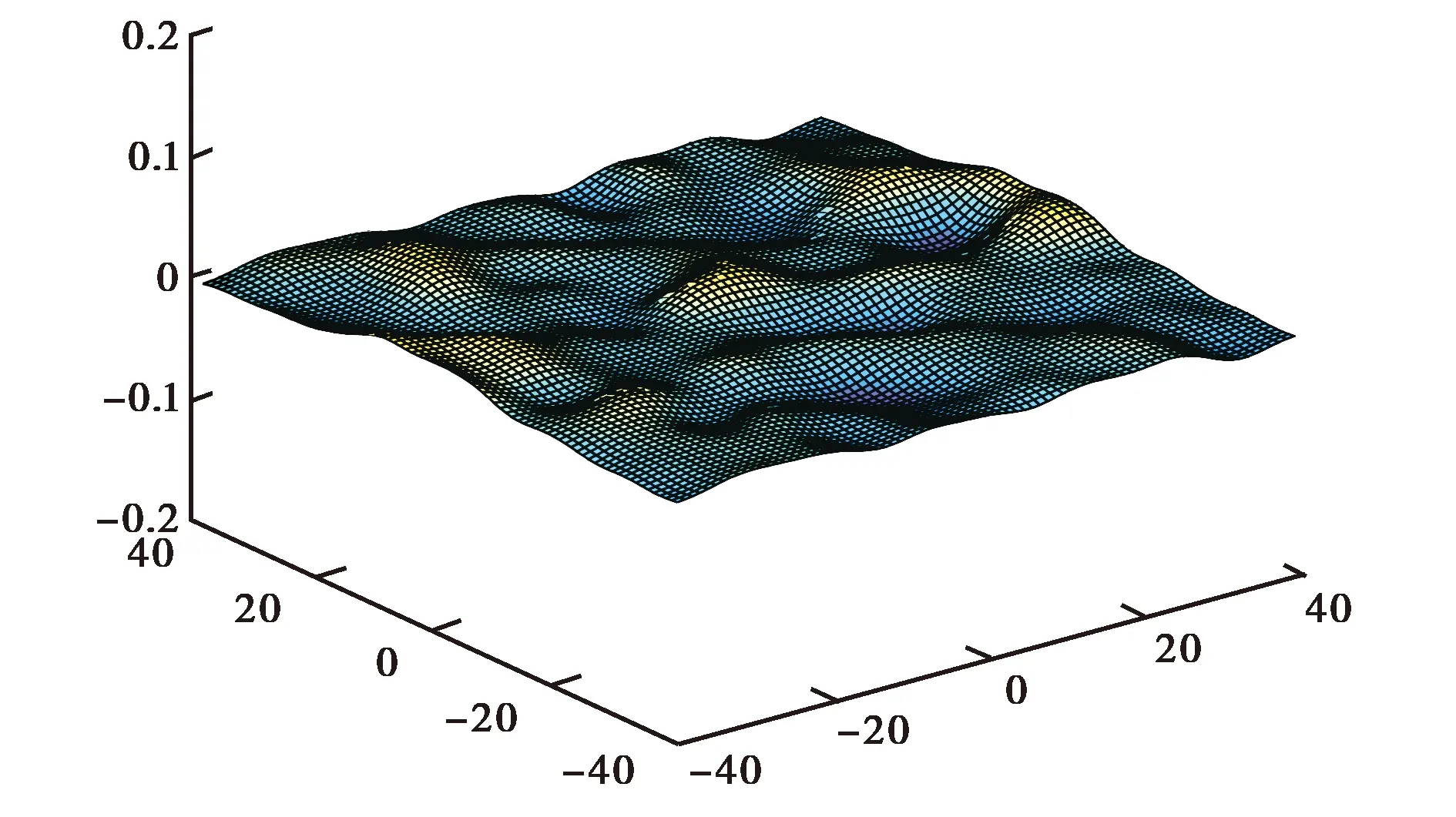
(b) η=1λ图2 相关长度η变化对粗糙面特性的影响

2 数值计算结果

我们以高斯随机粗糙平板为例,图3是一个尺寸为3λ×3λ,相关长度为0.1λ,均方根分别为0.01λ和0.05λ的粗糙面模型对应的散射结果,入射波为垂直入射的平面波,计算的双站RCS如图3所示.

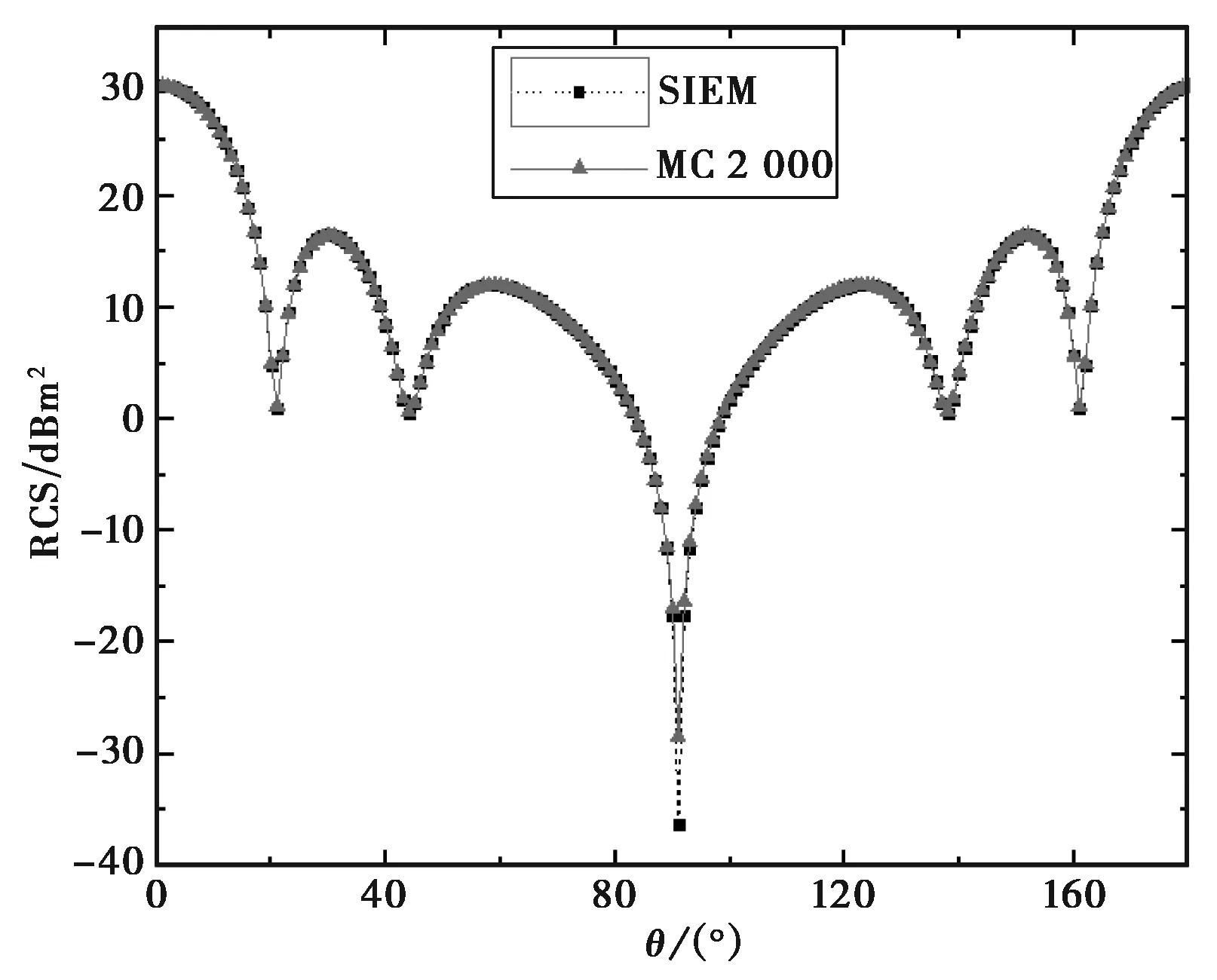
(a) σ=0.01λ

(b) σ=0.05λ图3 不同均方根对应的双站RCS

图3中虚线方块对应的曲线为SIEM的计算结果,实线三角对应为MC方法计算2 000次的结果. 从图3两个结果对比可以看出,均方根的值越小,计算结果与MC越吻合,这也说明了该方法更适合粗糙度较小的粗糙面. 经过我们验证,当入射波为垂直平面波相关长度大于0.08λ时,SIEM方法计算的结果误差较大.

图4是均方根为0.01λ,相关长度分别为0.1λ和0.5λ,粗糙面大小为3λ×3λ的高斯粗糙面RCS.

从图4可以看出,针对于不同的相关长度,SIEM跟MC方法都具有很好的吻合度,可见该方法对相关长度不敏感,所以可以用于不同相关长度的高斯粗糙面的计算.

(a) η=0.1λ

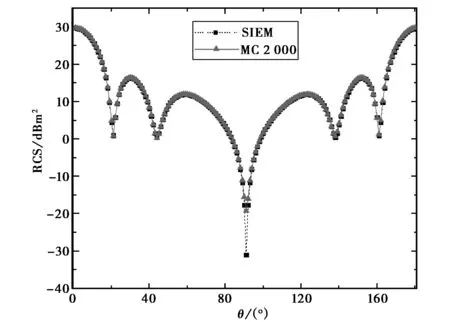
(b) η=0.5λ图4 不同相关长度对应的双站RCS

计算效率对比如表1所示.

表1 SIEM与MC计算时间对比

使用本文方法的计算速度大约是MC统计2 000次的8倍. 在上述算例中,MC选择2 000次统计,得到较好的结果,在相对复杂的结构中,MC需要更多的统计次数. SIEM体现出更好的效果, 所以该方法的研究具有很明显的意义.

3 结论与总结

经过理论推导和方法的实现,得出SIEM相对于MC方法具有很大的优势:第一,不需要进行精确的建模和重复多次进行求解;第二,该方法相对于MC方法具有更高的效率.

但是该方法也有局限性:第一,该方法更适合计算粗糙程度较小的粗糙面问题,特别是对应散射问题;第二,该方法只能局限于高斯分布的粗糙面问题.

在电磁波频率越来越高的背景下,SIEM具有很重要的研究意义.

[1] TSANG L, KONG J A, DING K H, et al. Scattering of electromagnetic waves[M]. New York: John Wiley & Sons, 2001:1-12.

[2] 逯贵祯, 林金才, 张文杰. 粗糙表面TE散射的Monte Carlo摸拟[J]. 北京广播学院学报, 2002, 3: 3-4.

LU G Z, LIN J C, ZHANG W J. Monte Carlo simulations of wave scattering from random rough surface for TE wave[J]. Beijing Broadcasting Institute journal, 2002, 3: 3-4. (in Chinese)

[3] ZHU Z H, WHITE J. A stochastic integral equation method for modeling the rough surface effect on interconnect capacitance[J]. IEEE computer society, 2004: 1-6.

[4] 盛新庆. 计算电磁学要论[M]. 2版. 合肥: 中国科学与技术大学出版社, 2008: 17-44.

SHENG X Q. A brief treatise on computational electromagnetics[M]. 2nd ed. Hefei: China University of Science and Technology Press, 2008: 17-44. (in Chinese)

[5] PETERSON A F, RAY S L, MITTRA R. Computational methods for electromagnetics[M]. New York: Wiley-IEEE Press, 1998: 10-19, 37-60.

[6] 金亚秋, 刘鹏, 叶红霞. 随机粗糙面与目标复合散射数值模拟理论与方法[M]. 北京: 科学出版社, 2008: 5-30.

JIN Y Q, LIU P, YE H X. Theory and method of numerical simulation of composite scattering from the object and randomly rough surface[M]. Beijing: Science Press, 2008：5-30. (in Chinese)

[7] 郭立新, 张民. 随机粗糙面与目标复合电磁散射的基本理论和方法[M]. 北京: 科学出版社, 2014: 1-30, 45-48.

GUO L X, ZHANG M. The basic theory and method of rough surface electromagnetic scattering of a target[M]. Beijing: Science Press, 2014: 1-30, 45-48.(in Chinese)

韩丹枫 (1990-),男,河南人,电子科技大学硕士研究生,研究方向为电磁场与电磁波散射.

胡俊 (1973-),男，浙江人，教授、博士生导师,主要研究领域为计算电磁学、电磁散射与逆散射、电波传播等.

聂在平 (1946-),男，陕西人，教授、博士生导师,研究方向为计算电磁学、电磁散射与逆散射、非均匀介质中的场与波等.

The calculation of scattering for Gaussian rough surface based on stochastic integral equestion method

HAN Danfeng HU Jun NIE Zaiping

(School of Electronic Engineering, University of Electronic Science andTechnologyofChina,Chengdu611731,China)

In this paper, we achieve the efficient computing of electromagnetic scattering for Gaussian rough surface based on the stochastic integral equation method(SIEM). Compared with the traditional method to solve the electromagnetic scattering the Monte Carlo method, SIEM only computes the matrix elements and the unknown current units once by using the statistical surface-unit Green’s function to couple the field and source, which is very efficient. The numerical results coincide with the Monte Carlo method very well and the computational efficiency is greatly improved.

Gaussian rough surface; stochastic integral equation method(SIEM); Monte Carlo method; electromagnetic scattering

10.13443/j.cjors.2015082201

2015-08-22

国家杰出青年科学基金(No.61425010)

O441.4

A

1005-0388(2016)03-0457-05

韩丹枫, 胡俊, 聂在平. 基于统计型积分方程的高斯粗糙面散射计算[J]. 电波科学学报,2016,31(3):457-461.

HAN D F, HU J, NIE Z P. The calculation of scattering for Gaussian rough surface based on stochastic integral equation method[J]. Chinese journal of radio science,2016,31(3):457-461. (in Chinese). DOI: 10.13443/j.cjors.2015082201

联系人： 韩丹枫 E-mail:danf_han@163.com