一种可应用于内燃机瞬态仿真的动网格模型
2016-11-29孙华文杨丽红明平剑张文平
孙华文, 杨丽红, 明平剑, 张文平
(1. 国家超级计算天津中心, 天津 300457;2. 国家知识产权局专利局专利审查协作天津中心, 天津 300304;3. 哈尔滨工程大学动力与能源工程学院, 黑龙江 哈尔滨 150001)
一种可应用于内燃机瞬态仿真的动网格模型
孙华文1, 杨丽红2, 明平剑3, 张文平3
(1. 国家超级计算天津中心, 天津 300457;2. 国家知识产权局专利局专利审查协作天津中心, 天津 300304;3. 哈尔滨工程大学动力与能源工程学院, 黑龙江 哈尔滨 150001)
提出了一种基于非结构网格的动态层网格实现算法,结合滑移网格算法构建了基于分块滑移动态层的非结构化内燃机动网格模型,并基于TBD620柴油机建立了计算模型,所有算法都基于课题组自主研发的通用输运方程求解软件实现。流场计算采用适用于可压缩流场的有限体积法及SIMPLE算法。通过数值算例对所开发的滑移网格模型和动态层网格模型进行了验证,最后对内燃机缸内瞬态流场进行了仿真。计算结果表明,所发展的非结构化动网格模型可应用于内燃机瞬态流场的仿真。
内燃机; 滑移网格; 动态层算法; 数值模拟
数值模拟作为一种有效的分析设计方法已广泛应用于内燃机的结构设计及性能分析中,然而现行的内燃机三维仿真分析软件大多来自国外,国内自主研发的相对较少。内燃机缸内瞬态流场仿真的关键技术主要包括运动网格处理、喷雾模型、燃烧及化学反应机理以及缸内流场数值求解方法等,其中处理好网格运动是一切物理模型应用的前提[1]。
对此国内外学者进行了针对性研究。A.Velghe等[2]采用全局的网格重构插值方法对内燃机的瞬态流场进行了仿真;D.Abouri等[3]研究了基于多面体网格的运动网格模型并应用于内燃机瞬态流场的计算;国内蒋炎坤、罗马吉等[4]研究了带气口发动机的瞬态流动计算,并利用SNAPPER技术解决运动边界问题;刘金武等[5]基于网格的拆解组合给出了内燃机缸内复杂空间三维动态网格的生成方法;秦文瑾等[6]基于KIVA3V进行了4 气门直喷式汽油机缸内湍流场多周期循环变动的大涡模拟研究,其中网格的运动主要依赖于KIVA3V中的自带模型。总体来说国外的内燃机动网格研究相对成熟,国内学者大多基于国外成熟算法或开源代码进行研究及改进,基于自主研发软件开发内燃机仿真平台研究内燃机动网格的较少。
本研究基于自主研发的通用输运方程求解软件[7-8]研究运动网格模型的实现算法,提出一种基于非结构网格的动态层网格实现算法,并针对内燃机运动网格的需求结合滑移网格算法提出了分块滑移动态层内燃机运动网格模型的解决方案,开发相应模块,为内燃机瞬态流场的仿真奠定基础。
1 数学模型
1.1 有限体积法离散
内燃机缸内流场的各基本控制方程最后都可以写成通用的输运方程形式:
(1)
方程由4个不同类型的项组成,依次称为瞬态项、对流项、扩散项和源项。其中源项又可以分为面积源项和体积源项。式中:φ为通用形式的场变量;Γφ为与φ相对应的扩散系数;SφA和SφV为与φ相对应的面积源项和体积源项。方程离散的目的是将方程转化成代数方程组的形式:
(2)
式中:nf为当前研究单元的面个数;j代表第j个面;φc0和φcj分别为当前所研究单元和第j个相邻单元在方程中的变量值;ap和aj分别为方程组中当前研究单元和第j个相邻单元在方程中的系数;bp为方程的源项。
方程的离散采用基于非结构同位网格单元中心的有限体积法,网格的形状可以是任意形状或者多种形状的混合网格。瞬态项采用中心差分的隐式格式求解,对流项采用一阶迎风格式,扩散项采用法向交叉方法。根据各项系数的贡献,可得方程组的系数分别为
ap=apT+apC+apD=
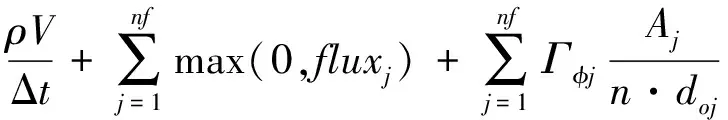
(3)
aj=ajT+ajC+ajD=
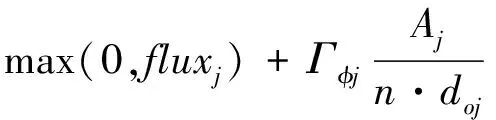
(4)
bp=bpT+bpC+bpD=
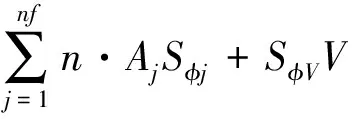
(5)
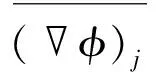
1.2 数值求解
采用非结构化网格的SIMPLE算法进行流场求解,采用Rhie-Chow[9]插值方法处理压力速度失耦问题,通过动量方程预测流场,再根据压力修正方程结果对压力场、速度场和单元面流量进行修正。适用于任意多面体网格及移动网格,可求解可压及不可压流动。基于SIMPLE算法求解包含移动边界流场的基本流程见图 1。
2 运动网格算法
2.1 滑移网格算法
由于网格区域间的滑移将会产生滑移面上网格间对应关系的不匹配(见图 2),要想知道网格间的对应关系,就要进行网格单元面之间的相交判断,本研究采用AABB(Axis Aligned Bounding Box)算法[10]进行计算。下面以二维情况为例说明AABB算法的基本原理。
二维时网格的单元面为线段,图3示出两相交单元,其中线段AB及线段CD需要进行相交判断,并假设线段AB为主要边界上单元面。AABB方法主要是采用建立包围盒来包围所需判断单元面,二维时包围盒为四边形,图4中的四边形1及四边形2分别为线段AB及线段CD的包围盒,由于包围盒的四边分别与坐标轴平行,因而只需存储四边形中两个节点坐标便可以确定此包围盒。为方便后续比较,采用存储XY坐标均最小的点及XY坐标均最大的点的坐标来确定包围盒,计算得到扩展包围盒BOX后,通过比较BOX与BOX_CD的最大最小点坐标来判断BOX是否包含BOX_CD,如果包含则表明单元面AB与单元面CD相交。由此便完成了AABB算法的二维单元面相交判断,该方法同样也可以应用于三维情况。
通过对两个不匹配边界的单元面进行循环便可得到不匹配边界上网格的对应关系,形成新的内部单元面,具体流程见图5。
2.2 动态层网格模型
动态层模型是利用增加或删减网格层来适应边界的运动,该方法对网格的划分及边界的运动形式要求较高,边界运动主要为往复式直线运动,网格需要在动边界运动方向上分层,因而常用于结构化网格,也称为层动网格。对于非结构网格存在网格间拓扑不规则的问题,主要通过网格层间的拓扑结构进行网格层的查找、增加及删减。
自主软件读入网格文件后,非结构网格间的基本拓扑关系便为已知信息,包括单元面两侧单元序号、构成单元的单元面序号等,且节点在单元中均有一定的排序,存储方式可参见文献[11]。本研究网格动态层的分层存储便是基于已知的非结构网格间的拓扑结构进行的,重新查找存储形成一个结构体数组来记录每层网格的信息。如图6网格含有一个层动边界,DE,EF,GH,HI代表着单元面的序号,所形成的结构体数组见表1。
获得层动网格信息后,在边界运动过程中,通过网格节点坐标替换及网格标记阻断相结合的方法来满足增减网格层时网格拓扑结构的变化。以图 7中网格2为例,当网格2由于层动边界运动被压扁需要删除时,只需将节点E及节点F的坐标分别赋给节点C和节点D,节点E及节点F的坐标恢复初始位置,之后将网格2标记为无效单元便完成网格2的删除,这样遍历层动边界上的网格便可达到网格层的删除。采用网格层存储算法得到的网格层信息中已将需要相互替换节点的单元面查找出并将节点排序一一对应,因此在网格删除及添加时直接替换即可。这种方法不需要网格及网格面的重新排序,整个过程网格结构不发生改变,且可以处理包含多个层动边界的情况。增加网格层时同上。所采用增加或删减网格层的判据为给定一个(0,1)之间的系数a,当层动边界网格高h
2.3 三维内燃机运动网格模型
以TBD620柴油机为例,带有进排气道的缸内流场模型见图8,其中左侧气阀为进行阀,右侧气阀为排气阀,且均处于全开状态,其中心截面见图9。
图10中区域划分依据分块滑移动态层法的需要进行,其中区域1,2,3,4,7,8,11为层动区域,因而这些区域的网格划分需要在层动边界的移动方向上分层。区域1,2,3,4,7,8的下边界均为层动边界,上边界为内部边界,即与相连区域公用此边界;区域11的下边界及上边界中的气阀下底面边界为层动边界。滑移边界主要有区域11与区域1,2,7,8的连接边界,区域7与区域5、区域8与区域6的连接边界,区域5,6与区域10的连接边界,区域3的左边界,区域4的右边界。区域3与区域5、区域4与区域6及区域11与区域12的连接边界为静止的不匹配边界面。进气阀上表面区域5及区域6为跟随气阀运动区域,这两区域的划分是为了适应进气阀表面的形状。
为进一步说明,图 11示出层动区域及滑移边界的应用示意图。虚线为静止的不匹配网格边界,主要有两个,一个是气道区域与气阀区域的衔接处,一个是燃烧室区域与气缸区域的衔接处;实线为滑移边界,主要在气阀内部区域及外部区域的交界处以及气阀外部区域与气缸区域的交界处。图中区域2为跟随气阀运动区域,区域1为适应阀杆运动的层动区域,区域3为适应气阀上表面运动的层动区域,区域5为适应活塞运动的气缸层动区域,区域4为适应气阀底部及活塞运动的层动区域。
假定初始时刻活塞位于上止点,进排气阀均为关闭状态,采用上述方法得到的不同曲轴转角时TBD620柴油机三维网格模型的运动结果见图12,该款柴油机的基本参数见表2,活塞的运动规律根据转速、行程、连杆长度及曲轴转角计算得到。

表2 TBD620柴油机基本参数
可以看到,所采用的分块滑移动态层法可以很好地适应TBD620柴油机工作过程中气阀及活塞的运动,整个过程中除运动边界上的网格需要调整外,其余网格均为静止状态。
3 数值应用
3.1 顶盖驱动方腔流动
顶盖驱动方腔流动算例是检验CFD程序的标准算例,本研究采用该算例验证所应用不匹配边界面算法在层流计算时的准确性。采用两种不同的网格划分形式,如图 13所示,其中网格1为均匀网格划分,不包含不匹配边界面,网格2采用不均匀网格划分,包含不匹配边界面。图13c为网格2中的实线围成区域的放大图,并给出了不匹配边界处的边界设置,其中包含两对不匹配边界面,分别为边界1与边界2,边界1与边界3,其中边界1与边界2的划分形式相同,边界1与边界3划分形式不同,存在不对应关系。方腔边长为1 m,采用的流体介质为水,密度为1 000.0 kg/m3,黏性系数为1.0×10-3kg/(m·s),上边界速度为0.000 1 m/s,即计算雷诺数为100,边界均为无滑移壁面边界条件。
图14示出采用两种网格计算得到的压力云图分布对比。可以看到,不匹配边界面的存在并未对结果产生影响。图15示出两种网格X方向及Y方向中心线的速度分布与文献[12]标准值的对比,两种网格的计算结果均吻合较好,说明了本研究采用的流场求解方法及不匹配边界面算法的准确性,也验证了所开发程序的计算能力。图16示出采用两种网格计算得到的压力残差对比,可以看到少量的不匹配边界面并未对残差的总体收敛趋势造成影响,但可以看到网格2的收敛还是慢于网格1,说明不匹配边界面对计算的收敛产生了影响。
3.2 缸内空气压缩膨胀过程模拟
对缸内空气的压缩膨胀过程进行模拟,取缸内平均压力值与理论值进行比较。假设压缩膨胀过程为绝热过程,则理论压力可由下式计算得到:
pn=εγp0。
式中:pn为当前压力;ε为当前容积与初始容积的比值;γ为理想气体绝热指数;p0为初始压力。
图17、图18分别示出本算例二维及三维初始网格,缸径为170mm,高度为200mm,行程为195mm,底面边界为运动边界,向顶面作周期为360°的压缩膨胀运动,在此算例中压缩比为40,采用动态层网格模型适应底面边界的运动进行流场计算。图19示出了计算得到的缸内平均压力值与理论值的对比,可以看到计算值与理论值吻合较好,从而验证了动态层模型与现有求解器结合的正确性。
3.3 二维内燃机缸内瞬态流场仿真
采用二维内燃机运动网格模型进行TBD620柴油机瞬态流场的仿真计算。假定初始时刻(0°曲轴转角)活塞位于存在气阀重叠角的上止点,配气定时如图 20所示。给定进口为速度进口,来流速度为2 m/s,出口为压力出口,初始时刻缸内空气密度为1.1 kg/m3,压力为0.1 MPa,温度为300 K,计算采用的曲轴转角步长为0.5°。计算得到不同曲轴转角下缸内流场的流线分布(见图21),可以清楚地看到不同曲轴转角下缸内流场的分布及燃烧室内气相漩涡的形成过程,符合真实情况,说明了本研究所开发的非结构内燃机运动网格模型的实用性。
4 结束语
基于自主开发的通用输运方程求解软件发展了一种新的基于非结构网格的动态层模型实现算法,并应用分块滑移动态层思想构建了非结构化内燃机动网格模型。通过顶盖驱动方腔流动算例和缸内空气压缩膨胀过程模拟的算例验证了所开发滑移网格和层动网格算法下流体流动数值模拟的正确性。最后,以TBD620柴油机模型为例建立了三维内燃机缸内流场运动网格模型,对二维内燃机瞬态流场进行了仿真,计算结果表明本研究提出的网格运动模型可较好地适应内燃机的瞬态流场计算中边界运动,且可以便捷地加入到现有流动求解器中。
[1] 张志荣, 冉景煜, 张力浦. 内燃机缸内气体CFD瞬态分析中动态网格划分技术术[J]. 重庆大学学报,2005,28(11):98-121.
[2] Velghe A, Gillet N, Bohbot J. A high efficiency parallel unstructured solver dedicated to internal combustion engine simulation[J]. Computers & Fluids,2011,45:116-121.
[3] Abouri D, Zellat M, Desoutter G, et al. Advances in combustion modeling in STAR-CD: a new technique for automatic grid and mesh motion generation applied to Diesel combustion and Emissions analysis[C]//19th International Multidimensional Engine User’s Meeting at the SAE Congress. Detroit:SAE,2009.
[4] 蒋炎坤, 李仁旺, 罗马吉,等. 发动机瞬态数值模拟中气口网格生成技术研究[J]. 华中科技大学学报,2001,29(5):14-16.
[5] 刘金武, 龚金科, 钟志华,等. 内燃机缸内复杂空间三维动态网格生成技术[J]. 计算机辅助设计与图形学学报,2006,18(4):488-492.
[6] 秦文瑾, 解茂昭, 贾明,等. 4气门直喷式汽油机缸内湍流场多周期循环变动的大涡模拟[J]. Journal of internal combustion engine,2012,30(3):234-240.
[7] 明平剑. 基于非结构化网格气液两相流数值方法及并行计算研究与软件开发[D]. 哈尔滨:哈尔滨工程大学,2008.
[8] 雷国东. 非结构网格FVM在复杂几何结构的湍流反应流计算中的应用研究[D]. 哈尔滨:哈尔滨工程大学,2008.
[9] Rhie C M, Chow W L. Numerical Study of the Turbulence Flow Past an Airfoil with Trailing Edge Separation[J]. AIAA Journal,1983,21(11):1525-1532.
[10] James M Van Verth, Lars M Bishop. Essential Mat-hematics for Games and Interactive Applications[M]. 2nd Edition.[S.l.]:Elsevier Inc,2008.
[11] 刘永丰. 基于非结构网格的缸内两相反应流数值模拟方法研究及软件开发[D]. 哈尔滨:哈尔滨工程大学,2013.
[12] Ghia U, Ghia K N, Shin C T. High Resolutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method[J]. Journal of Computational Physics,1982,48:387-411.
[编辑: 潘丽丽]
Dynamic Mesh Model Applied to ICE Transient Simulation
SUN Huawen1, YANG Lihong2, MING Pingjian3, ZHANG Wenping3
(1. National Supercomputer Center in Tianjin, Tianjin 300457, China;2. Patent Examination Cooperation Tianjin Center of The Patent Office, Tianjin 300304, China;3. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)
A new dynamic layer mesh algorithm based on unstructured mesh was introduced and the dynamic mesh model of internal combustion engine(ICE) was built by combining the sliding mesh algorithm based on the sliding dynamic layer. The calculation model of TBD620 diesel engine was further established and all the referred algorithms were realized through the self-developed general transport equation solver. The finite volume method and SIMPLE algorithm for the compressible fluid were utilized in the simulation. Moreover, the sliding mesh model and dynamic layer mesh model were verified through the numerical examples and finally the in-cylinder transient flow field of ICE was simulated. The results show that the introduced dynamic mesh method can realize the transient flow field simulation of ICE.
internal combustion engine(ICE); sliding mesh; dynamic layer algorithm; numerical simulation
2015-12-14;
2016-03-21
孙华文(1988—),男,硕士,研究方向为计算流体力学;sun_hua_wen@126.com。
10.3969/j.issn.1001-2222.2016.04.002
TK432
B
1001-2222(2016)04-0007-07
