探讨函数压轴题的解决方略
2016-11-28付刚
付刚
在备战中考的过程中,有一个非常重要的环节就是对函数问题的复习。函数问题经常作为压轴题出现在试题中,笔者特意关注了一下近几年的中考题,特别是函数压轴题。在此就笔者的一点想法呈现给大家,希望大家不吝赐教。
一、选择题中的压轴题
在中考试题中,函数问题的考察往往作为选择题的压轴题,题目偏难,且学生如果思考不全面很容易在最后环节出错。所以在考前复习时,学生不但要注重基础知识的掌握,更重要的是如何将知识升华为解题能力。
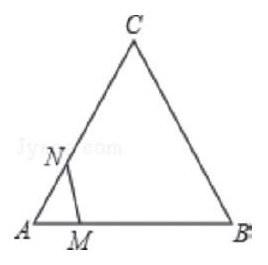
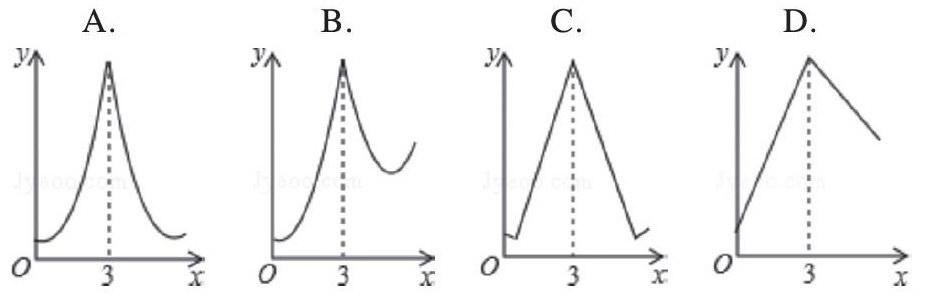
第一题:(2013·莱芜·12)如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )
解析:学生完全可以用估计和排除相结合的方法来解决问题,首先:①当动点M从A点出发到AM=1的过程中,y随x的增大而减小,故排除D;②当动点M到达C点时,x=6,y=3-1=2,即此时y的值与点M在点A处的值不相等。故排除A、C,故此题选B(中考的题目都是经过严格审查的,解决本题应首先看清横轴和纵轴表示的量,然后根据动点的行程判断y的变化情况,不一定要通过求解析式来解决。另外,解此题的关键在于利用特殊点来判断函数的增减性)。
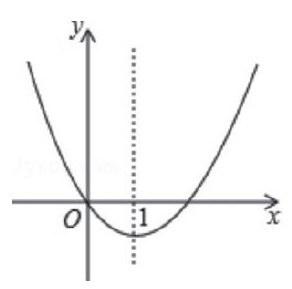
第二题:(2014·济南·15)二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx-t=0(t为实数)在-1 A. t≥-1 B. -1≤t<3 C. -1≤t<8 B. 3 解析:这个题目是学生出错比较多的一个题目,首先我们要变化一元二次方程x2+bx-t=0(t为实数),即t=x2+bx,利用对称轴直线x=1先求出b=-2,得t=x2-2x。我们结合图像仔细分析不难看出,在-1 二、解答题中的压轴题 二次函数压轴题是学生很头疼的题目,因为它往往把知识点综合起来考查,既考查二次函数的图象与性质、待定系数法,又考查函数图象上点的坐标特征、平移变换、图形面积计算等知识点,有些还结合平行四边形、相似三角形来考查,题目难度大。在复习过程中,学生要沉住气静下心来,不要惧怕这种题型,要庖丁解牛,一点点地分化难度,这样问题就迎刃而解了。 本文中的题目可以说是真正的压轴题,考察的是基础知识和数学思维能力,通过压轴题的分析,笔者认为在中考教学的复习中应从以下几个方面入手解决。 一是教学中要注重基础知识与方法的培养,并对其进行升华,以适应灵活运用的需要。这就要求教师在日常教学中,既要准确把握问题的内涵与外延,又要重难点突出,松弛有度。 二是要注重对题目解题思想方法的探究、思维形成过程的追踪以及对隐藏在题目背后的数学问题本质的挖掘与拓展。对一些典型的习题,要舍得花时间对其多角度、多方面地深入探究,让学生独立思考问题,充分暴露其思维过程,要让学生亲自体验、比较感受各种解题思想方法的优劣,进而得到质的飞跃。 三是在复习期间,注意加强学生严密逻辑推理能力的训练。在问题讲解过程中,教师也要注意节奏、时机的把握,对一些关键地方、重难点要及时追问。
