基于时空序列模型的RBF神经网络在河流水位预测中的应用
2016-11-28李欣王超赵虎川
李欣,王超,赵虎川
(1.济南市勘察测绘研究院,山东 济南 250101; 2.山东省城市空间信息工程技术研究中心,山东 济南 250101;3.武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 4.天津测绘院,天津 300381)
基于时空序列模型的RBF神经网络在河流水位预测中的应用
李欣1,2*,王超3,赵虎川4
(1.济南市勘察测绘研究院,山东 济南 250101; 2.山东省城市空间信息工程技术研究中心,山东 济南 250101;3.武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 4.天津测绘院,天津 300381)
河流水位预测一直以来都是水文预报中研究的热点。河流水位变化不定,具有时间上和空间上的变化性、多维性、动态性和不确定性等,给水位预测带来了挑战。本文综合考虑河流水位时空信息,建立基于时空序列的RBF神经网络预测模型来预测河流水位。实验中预测了金沙江下游向家坝水文站的水位信息,并将实验结果与其他多种水位预测方法比较,实验结果显示基于时空序列的RBF神经网络模型在河流水位预测中具有较高精度,证明了方法的可行性。
河流水位预测;水文预报;时空序列;RBF神经网络
1 引 言
水文预报是根据已知的水文信息对未来一定时期的水文状态做出定性或定量的预测[1]。作为水文预报的重要内容,河流水位预测对于水库调度、洪水控制、发电、灌溉等工作至关重要。然而,由于河流水位变化复杂,具有时间上和空间上的变化性、多维性、动态性和不确定性等特点,给河流水位预测带来了困难。
目前,水位预测方法大致分为过程驱动模型方法和数据驱动模型方法两类[2]。过程驱动模型是指以水文学概念为基础,对径流的产生过程与河流演进过程进行模拟,从而建立水位过程预报的数学模型。数据驱动模型则基本不考虑水文过程机制,而是以建立输入、输出数据之间最优数学关系为目标的黑箱子方法。随着水文数据的获取能力和计算能力的飞速发展,数据驱动模型在水位预测中也得到越来越多的应用,常用的数据驱动模型有回归模型、神经网络模型、非线性时间序列分析模型和灰色系统模型等[3~7],这些方法有各自的特点,适用于不同的情况中,比如时间序列分析法适用于短期预测,而中长期预测效果较差,灰色系统理论预测结果不确定性十分明显。
由于河流水位变化的非线性特点,而人工神经网络模型的适应能力和学习能力在非线性系统预测中具有较好的效果[8~10],本文采用RBF(径向基函数)神经网络模型进行河流水文预测。同时,考虑到河流水位在时间上和空间上的变化是相互联系、相互影响的。因此,本文在对河流水位进行预测、建立神经网络模型之前,综合考虑河流水位信息的时间和空间特性,采用向时间序列中嵌入空间对象子序列的思想,构建时空序列模型[11],提高河流水位的预测精度。
2 河流水位时空序列模型
河流的水位具有典型的时空特征,水位数据是根据沿河流分布的测站进行采集,某一测站的水位不仅随时间成规律性变化,同时在空间上也受到临近测站水位的影响,表现出时间上和空间上的连续性和渐变性。
考虑到河流水位信息的空间特征,把河流水位空间位置抽象为空间上的一维拓扑关系,把河流抽象成为一维线状地物,河流上的测站抽象为按一定间隔和方位分布的点状地物,以测站的水位作为地物之间联系,建立河流水位信息空间序列。
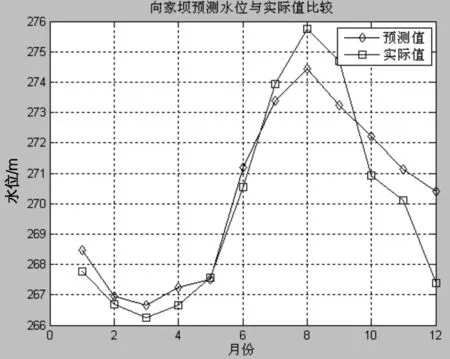
空间序列根据时间序列的思想扩展而来。将某种随机变量按出现的时间顺序排序起来称为时间序列。时间序列是对某一个或一组变量x(t)进行观察测量,将在一系列时刻t1,t2,…,tn(t为自变量且t1 x(t)={x(ti),i=1,2,…n} (1) 式(1)中,ti表示第i个时刻,n表示x(t)序列中包含的元素个数。 根据时间序列的表示方式,空间序列可以表示为空间上连续或离散分布的对象间一系列关系值的描述。对某一个或一组变量x(s)进行观察测量,s表示空间位置,将一系列具有空间关系的对象s1,s2,…,sn之间的联系的离散观测值组成的序列集合x(s1,2),x(s1,3),x(s1,4),…,x(s2,3),x(s2,4),…,x(sn-1,n),把它称之为空间序列,表示如下: x(s)={x(si,j),i=1,2…,n;j=1,2,…,n;i≠j} (2) 式(2)中,n为空间序列集合中包含的对象个数;si,j则表示为这些对象间的方位关系,x(si,j)为对象i和对象j之间的联系值。 根据上述方法建立起来的空间序列,结合本文河流水位信息空间分布特点,根据河流不同位置(测站)水位之间的相互影响抽象出如下的空间序列模型,如图1所示。 图1 河流水位空间序列模型 图1中黑色实线和箭头表示河流水流方向。s1,s2,…,sn则是由河流上的测站抽象而成,具有顺序的临近关系。s1,2,s1,3,…,sn-1,n表示这些空间对象之间的关系,x(s1,2),x(s1,3),…,x(sn-1,n)表示为这些空间对象之间的联系值。 时空序列建模分为在空间序列中插入时间序列和在时间序列中插入空间的方法。针对时空因素对河流水位的重要作用,本文采用把空间子序列作为时间序列的一个元素嵌入到时间序列中去,形成时空序列模型。根据式(1)和式(2)所示,在时间序列中嵌入空间序列,即是把时间序列中的每一个元素用空间序列来表示,空间序列中保留了各个空间对象和它们之间的联系值,这些空间对象间的联系值随时间发生相应变化。把式(2)中的空间序列x(s)作为式(1)中时间序列x(t)的一个元素,则式(1)变为: f(t)={ti(sj,k),i=1,2,…,m;j,k=i,2,…n,j≠k} (3) 式(3)中,ti(sj,k)代表了在时间i时,空间对象j和空间对象k之间的联系值。 根据上述方法建立的模型如图2所示。本时空序列模型,本质上是先建立空间序列模型,然后在时间序列中嵌入空间序列。本文的研究对象是针对河流水位的时空序列建模,本模型很好地表达了空间对象的空间关系和随时间变化的情况,反映了河流水位在时间上和空间上动态变化和相互联系的特征,把河流水位信息的时间、空间和属性信息融合到一起。 RBF神经网络是Moody和Darken与20世纪80年代末提出的一种具有单隐层的三层前馈网络。输入层由信号源节点组成;第二层是隐层,隐层的变换函数是RBF,它是对中心点对称且衰减的非负非线性函数;第三层为输出层,它对输入模式的作用做出响应[14,15]。与其他前馈型神经网络相比,RBF神经网络具有良好的函数逼近性能,若RBF神经网络的隐含层神经元个数足够多,则RBF神经网络可以一致连续逼近任何连续函数。 利用RBF神经网络进行预测,首先要构建其网络模型,在建立RBF神将网络时,各层的节点数目、RBF、隐层中心、扩展常数和隐层到输出层的权值都是需要考虑的因素。把之前建立的时空序列模型结合RBF神经网络建立如下神经网络预测模型,如图3所示。 图3 基于时空序列的RBF神经网络模型 本文选取金沙江下游2009年8月~2013年12月的二期围堰上、沙湾、一期围堰下、二期围堰下和向家坝水文站5个站的月平均水位数据作为原始数据。运用时空序列模型对这5个站的水位数据进行时空融合建模,然后结合RBF神经网络进行河流水位预测,并将预测结果和其他河流水位预测方法进行比较分析,实验流程如图4所示。 图4 实验流程 4.1 研究区域概况 金沙江为长江上游干流,发源于青藏高原唐古拉山西南,至四川宜宾。全长 2 316 km,流域面积34万km2。金沙江是我国重要的水电生产基地,研究金沙江水位变化,对水电开发和河流治理都具有重大意义。 4.2 河流水位时空序列建模 本文选取金沙江下游二期围堰上、沙湾、一期围堰下、二期围堰下和向家坝水文站5个站为研究对象。根据建立的河流水位空间序列模型,结合金沙江下游5个测站的空间关系,建立如图5所示模型。 图5 向家坝河流水位空间序列模型 河流水位时空数据模型 表1 采用5个测站2009年8月到2013年12月共53个月的月平均水位数据。考虑到向家坝上游4个测站对它水位的影响构建如表1所示的河流水位时空序列模型。在模型中,Eqs(1)为二期围堰上水位站2009年8月的月平均水位,…,以此类推,Eqs(53)为二期围堰上水文站2013年12月的月平均水位;同样,对沙湾、一期围堰下、二期围堰下和向家坝水文站分别以Sw(n),Yqx(n),Eqx(n)和Xjb(n)表示第n个月的月平均水位(n=1,2,…,53)。将二期围堰上、沙湾、一期围堰下、二期围堰下水文站连续3个月的水位数据和向家坝水文站第4个月的水位数据组成一个相应的时空序列进行建模研究,即将Xi,Xi+1,Xi+2,Xjb(i+3)作为一个时间序列(i=1,2,…,50)。在这个序列中融合了河流水位的空间和时间因素,其中Xi,Xi+1,Xi+2将作为RBF神经网络的输入因素,而相应的Xjb(i+3)将作为RBF神经网络的输出因素(i=1,2,…,50)。 4.3 RBF神经网络初始化与参数设定 将样本数据分为训练样本和预测样本两部分:训练样本。训练样本选择2009年8月~2012年12月二期围堰上水文站到向家坝水文站的月平均水位数据。根据表1的规则,2009年8月~2009年10月,二期围堰上、沙湾、一期围堰下、二期围堰下水文站连续三个月的水位数据预测向家坝2009年11月水位数据,……,2012年9月~2012年11月,前4个测站连续3个月水位数据预测向家坝2012年12月的水位。这样,共生成38组训练样本。为了避免过拟合,允许误差不宜过小,训练样本不宜过多。将38组训练样本分为两部分:前24组训练RBF网络的各个参数,其余14组作为检验网络的性能,并对网络参数进行调整,以防止网络过拟合,增加泛化能力。预测样本:以5个测站2012年10月~2013年12月共15个月数据作为预测样本数据。根据前4个测站2012年10月~12月的水位数据预测向家坝2013年1月的数据,…,根据前4个测站2013年9月~11月的河流水位数据预测向家坝2013年12月的数据,从而共得到12组预测样本数据。将RBF预测模型得到的预测结果与实际值进行比较,从而证实该方法的有效性。 在构建RBF神经网络时,需要确定径向基函数的扩展速度(spread)和隐层神经元数目(MN),前者是随着值的增加,网络的泛化能力增强,拟合能力增强;后者随着值的增加,网络的拟合能力增加,泛化能力减弱。为此,需要找到两个参数的最佳组合,使得网络的性能得到最佳。本文采用k-means聚类算法对网络进行训练。通过调整参数不断训练,最终得到最优的(spread,MN)=(3,13)。网络训练及检验样本误差曲线如图6所示,所用时间为 0.236 9 s。 图6 spread=3.0,MN=13时网络检验相对误差曲线图 4.4 RBF神经网络仿真预测与对比分析 依据上小一节建立的RBF神经网络预测模型,根据建立的12组预测样本数据,对2013年1月~12月的向家坝水文站水位进行预测,得到图7所示的网络预测值和实际值比较图和图8所示的误差曲线图。 向家坝2013年1月~12月的实际值、预测值、误差、相对误差等信息见表2所示。向家坝水文站从2013年1月~2013年12月水位预测最大误差绝对值为 3.018 5 m,最小误差绝对值为 0.259 4 m。由于12月份金沙江下游出现较大面积干旱,致使12月份水位预测比实际值偏高,预测误差偏大。除12月份外,其他11个月的误差绝对值都在 2 m之内,且相对误差也在1%之内。 图7 向家坝水文站水位预测值与实际值曲线图 向家坝2013年1月~2013年12月水位预测一览表 表2 为便于比较,实验中分别用未采用时空序列模型的RBF神经网络方法、逐步回归法、灰色系统法,对数据进行多次训练和预测。几种方法预测的水位误差比较如表3所示。 几种水位预测方法比较 表3 综上,基于时空序列模型和RBF神经网络的河流水位预测方法在水位预测精度上有很大提高。 本文在总结河流水位信息特点以及现有方法在水位预测中的不足的基础上,综合考虑了河流水位的时间和空间特性,采用时空序列模型对河流水位数据进行建模,并通过RBF神经网络对金沙江下游向家坝水文站的水位进行预测。通过和其他几种水位预测方法进行比较,结果显示基于时空序列模型和RBF神经网络的河流水位预测方法在水位预测精度上有很大提高,体现出较大的优势。 [1] 包为民. 水文预报[M]. 北京:中国水利水电出版社,2009:1. [2] 王文,马骏. 若干水文预报方法综述[J]. 水利水电科技进展,2005,25(1):56~59. [3] 陈斌,包为民,瞿思敏等. 双向线性回归法在椒江临海站水位预报中应用[J]. 水文,2008,28(3):45~48. [4] 王国成,柳林涛,徐爱功等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J]. 测绘学报,2014,43(8):803~807.[5] 谭兴龙,王坚,赵长胜. 神经网络辅助的GPS/INS组合导航自适应UKF算法[J]. 测绘学报,2015,44(4):384~391.[6] 沈晔,李海涛,黎涛等. 地下水位预测:集合卡尔曼滤波(EnKF)应用概述[J]. 水文地质工程地质,2014,41(1):21~24. [7] 刘政,邹长武,赵吉武等. BP神经网络模型拟合受回水影响的水位流量关系研究[J]. 水文,2008,28(6):28~30.[8] 王光生,苏佳林,沈必成等. 神经网络理论在河道洪水预报中的应用[J]. 水文,2009,29(5):55~58. [9] 陈田庆,解建仓,张刚等. 基于BP神经网络的马斯京根模型参数动态估计[J]. 水力发电学报,2012,31(3):31~38. [10] 王艳君,金生. 河网水情预测的三种BP神经网络方法比较[J]. 水电能源科学,2010,28(2):19~22. [11] 邓敏,陈倜,杨文涛. 融合空间尺度特征的时空序列预测建模方法[J]. 武汉大学学报·信息科学版,2015,40(12):1625~1632. [12] 陈飞香,程家昌,胡月明等. 基于RBF神经网络的土壤铬含量空间预测[J]. 地理科学,2013,33(1):69~74. [13] 王炜,吴耿锋,张博峰等. 径向基函数(RBF)神经网络及其应用[J]. 地震,2005,25(2):19~25. River Water Level Forecast Based on Spatio-temporal Series Model and RBF Neural Network Li Xin1,2,Wang Chao3,Zhao Huchuan4 (1.Jinan Geotechnical Investigation and Surveying Institute,Jinan 250101,China; 2.Shangdong Engineering Technology Research Center of Urban Spatial Information,Jinan 250101,China; 3.State Key Laboratory for Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079,China; 4.Tianjin Institute of Surveying and Mapping,Tianjin 300381,China) River water level prediction is not only an important part of hydrological forecasting,but also a hot topic. It is a challenge to river water level prediction,for its level fluctuation,time and space variability,multidimensional,dynamic and uncertainty. Considering the temporal and spatial information of river water level,this paper proposes a method based on spatio-temporal series model and RBF neural network,then predicts river water level of Xiangjiaba Station with the method. Moreover,the obtained results are compared to other forecast method. The experimental results show that the forecast method based on spatio-temporal series model and RBF neural network has the excellent performance of higher prediction precision. river water level prediction; hydrological forecasting;spatio-temporal series model; RBF neural network 1672-8262(2016)05-34-06 P641.6 A 2016—06—02 李欣(1984—),男,硕士,助理工程师,主要研究方向为地理信息系统。 国家高技术研究发展计划(863计划)(2013AA010308)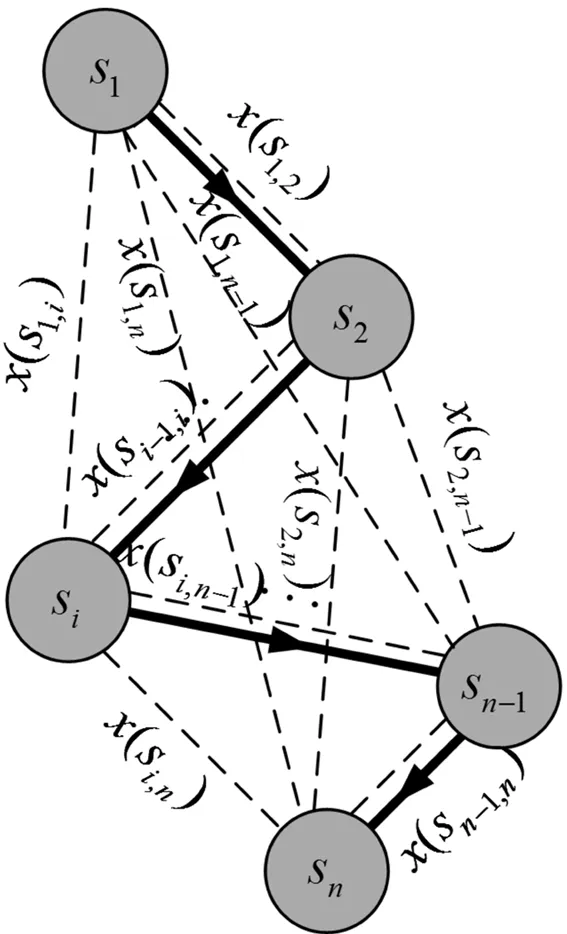
3 RBF神经网络模型

4 河流水位预测实验






5 结 论
