液压伺服系统时间最优模糊PID控制算法研究

王延年，黄俊龙

（西安工程大学电子信息学院，西安710000）

液压伺服系统时间最优模糊PID控制算法研究

王延年，黄俊龙

（西安工程大学电子信息学院，西安710000）

液压伺服系统是典型的非线性不确定系统，难以确立精确的数学模型，再加上工业现场复杂环境的干扰以及现代伺服系统对控制精度，响应速度，工作稳定性的更高要求，单一的控制算法显然无法满足系统的控制要求。因此需要把多种控制算法相结合，利用多种控制算法的优点，实现性能更优的多模复合控制。但是传统的阀值切换多模控制器存在切换点选取以及切换扰动的问题。针对上述问题，以伺服控制系统为研究对象，设计了一种基于偏差和偏差变化率的模糊规则无扰切换bangbang－Fuzzy－PID多模复合控制器。通过对实验结果分析，可以得出此多模复合控制器克服了阀值切换的缺点，实现了控制器之间的平滑过渡，达到了无扰切换的目的。

液压伺服系统；棒棒控制；模糊控制；PID控制；阀值切换；无扰切换

1　引　言

此复合控制基于模糊控制理论、快速时间最优控制原理与经典PID控制方法，将bangbang控制、模糊控制和PID控制加以结合，通过制定和设置相关的模糊规则与参数，设计了一种时间最优模糊PID控制算法，并利用模糊切换规则，解决了控制器控制算法间切换扰动大的问题。

2　液压伺服控制系统概述

液压伺服控制系统主要由伺服控制器、电液伺服阀、动力油站、液压油缸、位移传感器等组成。其结构如图1所示。

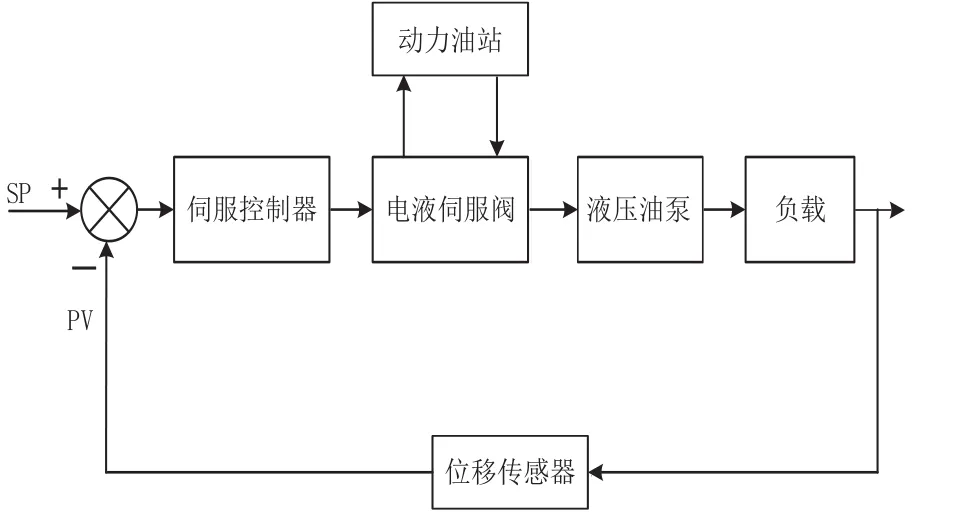
图1　液压伺服控制系统结构图

液压伺服控制系统的工作过程为伺服控制器通过对给定信号（SP）和反馈信号（PV）的比较，根据两者偏差的大小选择合适的控制算法，并将计算结果转换成电流信号，用来驱动电液伺服阀。电液伺服阀将电信号转换成液压油的油路和流量信号，驱动液压油缸活塞向消除偏差的方向运动，从而实现伺服系统的控制调节目的［2］。在整个伺服控制系统中，伺服控制器是控制核心，又因为控制算法是整个伺服控制器的决策核心，所以控制算法的选取直接关乎整个系统性能的优劣，因此控制算法的选择在伺服控制系统中至关重要。

3　经典控制算法

3．1经典PID控制

经典PID控制算法就是通过调整比例（P）、积分（I）、微分（D）三个参数间的大小关系使控制系统获得良好的闭环反馈控制效果。

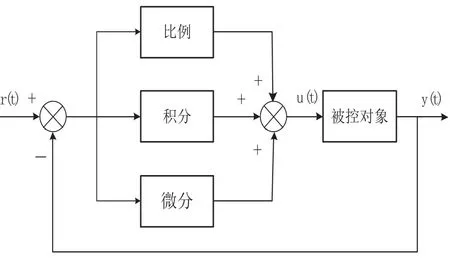
图2　经典PID控制原理框图

图2中r（t）是给定输入信号，y（t）是实际输出反馈量，e（t）为给定输入r（t）与实际输出y（t）的控制偏差，即：

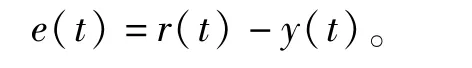
若PID运算输出结果为执行机构的控制增量，则称为增量式PID控制算法，其表达式为：

工匠精神是对心中目标的不懈追求，目标是方向，是动力。因为有目标才能不断努力，锲而不舍。因为有目标才知道未来的路如何走，才不至于迷茫。所以，目标是工匠精神之魂。现代科技发展日新月异，学生所学专业也在不断进步。培养新时代的工匠，教师要引导学生认清专业发展方向，让专业与现代科技相结合，在学习专业的同时要把握好专业的发展方向，为学生树立专业发展的目标。

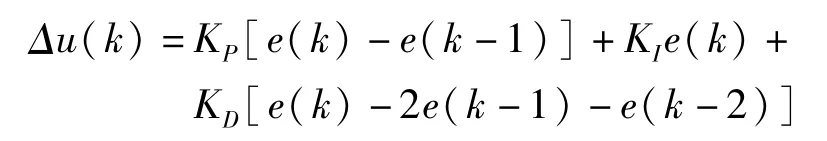
式中，KP、KI、KD分别为比例、积分、微分系数。通过以上分析可以发现，单纯的PID控制适用于具有精确数学模型的受控对象，适合解决相对简单的控制问题，对控制非线性、大滞后、变参量的系统控制效果不佳。因此，在面对较复杂系统时，需要和更加先进的控制算法结合，进行复合控制。

3．2Fuzzy控制

模糊控制是一种非线性化的数字式控制模式。模糊控制主要以规则表和模糊数学组成控制策略［3］，其核心思想就是模拟人的思维过程，把专家与现场操作人员的知识和经验等规则的语言表述采用模糊的推理方式转换成相对应的控制量，提供一种对难以建立精确数学模型的非线性系统的有效控制方法，图3为模糊控制器的结构框图。

图3　模糊控制器结构框图

与经典PID控制算法相比，模糊控制不需要精确的数学模型，为一种非线性PID控制，但在实际应用中，模糊控制无法实现精确控制，且由于模糊控制器对输入的精确数字信号进行了模糊化处理，降低了小偏差范围的控制精度和系统的动态品质。

3．3Bang－Bang控制

Bang－Bang控制又称为时间最优控制或快速控制，即控制系统的设定值发生变化时，系统从一个状态运动到另一个状态所经历的时间最短。当系统误差非常大时，适合采用Bang－Bang控制，即控制计算机输出的控制变量为最大值或最小值（负的最大值）。这种方法可使系统尽快向消除误差的方向运动。

4　多模复合控制

4．1时间最优模糊PID控制

通过对经典PID控制、模糊控制以及Bang－Bang控制算法的研究与对比，考虑到在实际的工业控制中，伺服控制系统是典型的非线性系统，再加上工业现场复杂环境的干扰以及现代伺服系统对控制精度，响应速度，工作稳定性的更高要求，单一的控制算法显然无法满足系统的控制要求。经典PID控制、模糊控制和Bang－Bang控制各自存在优势和不足，时间最优模糊PID控制算法解决了单独使用经典PID、模糊控制和Bang－Bang控制算法所带来的局限性，通过复合控制三者可以充分发挥自身优势。

4．2基于阀值切换的时间最优模糊PID控制

在设计时间最优模糊PID控制算法时，为了降低算法复杂度，同时避免经典控制的一些先天缺陷，根据系统整个控制过程的特性和行为，将偏差分为大偏差区、较大偏差区和小偏差区。三个偏差区分别采取不同的控制策略，既能解决控制系统中稳定性与准确性的矛盾，又能增强系统的抗干扰能力。

在大偏差区，系统偏差非常大，为尽快减小偏差，使系统以最快速度，向较小偏差的方向运动，需要最大的控制量输出。同时也希望在进入较小偏差区的时候，速度能够降低到一定的速率，以保证系统运行的稳定性。因此，在大偏差区，采用Bang－Bang控制，使系统先以最快速度减小偏差，在达到一定的偏差值时，开始减速，使系统在一定速度下进入下一个偏差区。在较大偏差区，模糊控制器起作用，系统有较快的响应速度和较高的控制精度，使偏差迅速进入更小偏差区。在小偏差区，采用PID进行精确控制，使系统具有更高的控制精度。

图4　阀值切换时间最优模糊PID控制系统

图4是基于阀值切换的时间最优模糊PID控制系统，阀值切换是程序根据事先设定的偏差范围自动切换。当偏差e＞eb时，属于大偏差区，输出控制量u为Bang－Bang控制器输出；当偏差ea≤e≤eb时，属于较大偏差区，输出控制量u为模糊控制器输出；当偏差e＜ea时，属于小偏差区，输出控制量u由PID控制器进行调整来消除余差。基于阀值切换多模复合控制算法简单、实时性好且具有较快的响应速度，能够消除稳态误差。但是阀值切换的切换点选取直接关乎整个控制系统的性能优劣，过早切换体现不出Bang－Bang控制和模糊控制的优点而使超调量过大；过迟切换则不能尽快消除稳态误差［4］。

因此，在进行切换时，为了保证控制量的输出连续，必须使在切换点的两种控制器的输出量相等，以保证系统在该点控制量输出不会出现跳变［5］。在复合控制中怎样实现无扰切换已经是工业控制中一个亟需解决的问题［6］。纯粹的切换点选择很难解决系统的快速性与超调之间的矛盾，需要寻找新的解决方案

4．3基于模糊规则切换的时间最优模糊PID控制

为了克服阀值切换的缺陷，文中采用了模糊规则的切换方式，设计了基于模糊规则切换的时间最优模糊PID控制器，如图5所示。

图5　模糊规则切换时间最优模糊PID控制系统

基于模糊规则切换的时间最优模糊PID控制器是按照模糊规则表1进行切换的。其中，UB、UF、UP分别为Bang－Bang控制器、模糊控制器和PID控制器的输出；μ，φ分别为模糊规则切换｜e｜和｜ec｜的隶属度函数。隶属度函数的形状关乎整个控制器的性能，通过改变ai（i＝1，2，3，4）的值可以改变隶属度函数的形状，从而改变系统的控制强度和动静态响应特性。当偏差和偏差变化率在采样的某个时刻为e（t）和ec（t）时，如图6所示。

表1　模糊切换规则表

图6　模糊规则切换隶属度函数

通过模糊规则对应图中的隶属度函数可以得到Bang－Bang控制器、模糊控制器和PID控制器的控制强度系数分别为WB、WF和WP，即

WP＝［μS（｜e（t）｜）×φS′（｜ec（t）｜）］（模糊蕴含积运算RP）

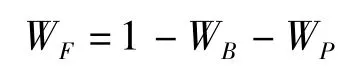
其中μB、μS和φS′分别表示偏差和偏差变化率相应模糊子集B、S和S′的隶属度函数。三个控制器的混合输出采用重心法运算，得

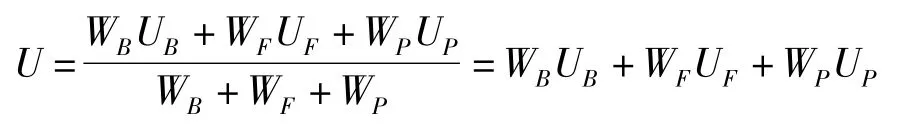
由上可知，系统在大偏差时Bang－Bang控制器起主要作用，在暂态过程中，由于系统偏差与偏差变化量均较大，此时模糊控制器起主要作用［7］；只有当系统进入稳态阶段，系统偏差与偏差变化量均很小时，PID控制器才起主要作用。故此多模控制器在大偏差时的Bang－Bang控制保证了控制器的快速性，在暂态时的模糊控制保证了控制器具有良好的跟踪性和较小的超调量，同时在稳态时的PID控制确保了控制器具有较高的控制精度。并且此多模复合控制器能够实现控制方式的平稳过渡［8］，消除了阀值切换在切换点附近区域扰动比较大的缺陷，也克服了阀值切换在稳态时没有发挥模糊控制器抑制干扰性的缺点。因此，此多模复合控制在兼备三种控制器优点同时，还具有良好的抗扰动能力。

5　控制效果与分析

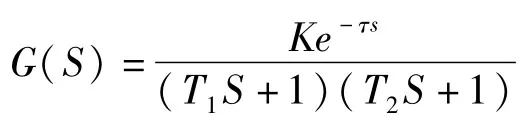
在三种模型下，把两种切换方式下的控制器参数分别调至最优，阀值切换点分别选取为最大误差的10%和90%处，可以得到两种切换方式下时间最优模糊PID控制器动静态性能指标，如表2所示。通过对这三个模型下的动静态性能指标比较我们发现，基于模糊切换的调节时间ts和超调量σ%都比阀值切换的要小。由此可以看出相比常规的阀值切换，模糊切换的响应速度更快，超调量更小，抗干扰能力更强，控制更加稳定。

表2　三个模型下两种切换方式的控制性能指标

6　结束语

提出的基于模糊规则切换的时间最优模糊PID控制器，可以在保留各控制器优点的同时，消除各控制器控制算法之间的切换扰动问题。它算法简单，易于实现［10］，具有较强的抗干扰能力，满足伺服系统较高的控制要求。

［1］孙增圻，邓志东，张再兴．智能控制理论与技术［M］．北京：清华大学出版社，2011．Sun Zen－qi，Deng Zhi－dong，Zhang Zai－ying．Intelligent control theory and technology［M］．Beijing：Tsinghua University Press，2011．

［2］王延年，郭卫松，陈苗苗．基于DSP的高精度智能电液伺服控制器的设计［J］．西安工程大学学报，2013（2）：198－202．Wang Yan－nian，Guo Wei－song，Chen Miao－miao．DSP－based high－precision smart electro－hydraulic servo controller［J］．Xi'an Polytechnic University，2013（2）：198－202．

［3］王正林，王胜开，陈国顺，王祺．MATLAB／Simulink与控制系统仿真［M］．北京：电子工业出版社，2012．Wang Zheng－lin，Wang Sheng－kai，Chen Guo－shun，Wang Qi．MATLAB／Simulink and ControlSystem［M］．Beijing：Electronic Industry Press，2012．

［4］荣盘祥，付刚，戴如俊．一种基于模糊规则切换的Fuzzy－PID双模控制器［J］．哈尔滨理工大学学报，2006（6）：8－12．Rong Pan－xiang，Fu Gang，Dai Ru－jun．Fuzzy－PIDdual－mode controller based on Fuzzy Rules Switching［J］．Harbin University of Science andTechnology，2006（6）：8－12．

［5］付刚．基于知识的智能PID控制器研究［D］．哈尔滨：哈尔滨理工大学，2007．Fu Gang．Intelligent PID Controller Based on Knowledge［D］．Harbin：Harbin University of Science and Technology，2007．

［6］从闯．基于Smith预估补偿的模糊－PID混合控制在时滞系统中的应用研究［D］．沈阳：东北大学，2008．Cong Chuang．Application of Fuzzy－PID mixed Smith Predictor Based Control System Delay［D］．Shenyang：Northeastern University，2008．

［7］李祖欣．复合控制一种简便模糊切换方法［J］．自动化技术与应用，2003（4）：11－13．Li Zu－xin．A Simple Fuzzy Compound Controlswitching method［J］．Techniques of Automation and Applications，2003（4）：11－13．

［8］李昌武．Fuzzy－PID复合控制器及其在温控系统中的应用［D］．长沙：湖南师范大学，2008．Li Chang－wu．Fuzzy－PID Composite Controllerand Its Application in Temperature Control System［D］．Changsha：Hunan Normal University，2008．

［9］陈丽华．多目标电液伺服系统模糊控制与实验研究［D］．哈尔滨：哈尔滨理工大学，2006．Chen Li－hua．Control and experimental study ofmultiobjective Fuzzy Servo System［D］．Harbin：Harbin University of Science and Technology，2006．

［10］曲秋江，于连胜．模糊pid控制器在复杂控制中的应用［J］．电子世界，2013（13）：102－102．Qu Qiu－jiang，Yu Lian－sheng．Fuzzy pid controller in the control of complex［J］．Electronic world，2013（13）：102－102．

Research of Time Optimal Fuzzy PID Control Algorithm in Hydraulic Servo Control System

Wang Yannian，Huang Junlong
（College of Electronic Information，Xi＇an Polytechnic University，Xi＇an 710000，China）

The hydraulic servo system，as a typical nonlinear uncertain system，is difficult to establish a precise mathematical model．Because of the interference of industrial field environments and the high requirements of modern complex servo system for control precision，response speed and job stability，the single control algorithm is clearly unable to meet the requirements of the control system．A variety of control algorithms are combined，using the advantages of control algorithms to achieve better performance of complex multi－mode control．But the problems such as select switching point and switch disturbance exist in traditional threshold switch multimode controller．For the problems mentioned above，the servo control system is used as the research object and a multimode Composite Controller of the fuzzy rules bumpless switching is designed，based on the deviation and the deviation change rate．The experimental results show that the multi－mode controller overcomes the shortcomings of the threshold switch，realizes a smooth transition between the controllers and achieves the purposes of bumpless switching．

Hydraulic servo system；Bangbang control；Fuzzy control；PID control；Threshold switch；Bumpless switching

10．3969／j．issn．1002－2279．2016．05．012

TP273

A

1002－2279（2016）05－0048－04

王延年（1963－），男，吉林省长春市人，教授，主研方向：工业控制系统及信息网络。

黄俊龙（1988－），男，江苏省徐州市人，硕士研究生，主研方向：工业控制系统及信息网络。

2016－02－29