初中数学含参数问题的处理策略
2016-11-28曾立萱
曾立萱
(泉州市第七中学金山校区 福建泉州 362000)
初中数学含参数问题的处理策略
曾立萱
(泉州市第七中学金山校区 福建泉州 362000)
参数是用字母表述的,它兼有常数和变数的双重特征。参数问题将思维和运算有机地结合在一起,能有效地考查考生的思维能力、运算能力。在解决含参数的问题时常根据已知条件列出含参方程或不等式,再求出参数的值或取值范围。在几何中用参数更容易体现几何元素之间的等量关系,从而更好地解决几何题。
参量 多元方程组 不等式组 主元 待定系数法 函数最值 几何代数化 消参 定值
在初中数学中运算能力的考查主要是以数的计算、含字母的式的运算为主,同时兼顾对算理和逻辑推理的考查。参数是用字母加以表述的,它兼有常数和变数的双重特征。参数问题能有效地考查考生的思维能力、运算能力、推理能力,是近年来中考命题的常见题型。如何在初中数学教学中有效地引导学生解决含有参数的问题?笔者结合自身的教学实践谈谈含有参数问题的几点处理策略。
一、用字母代替数,在数学计算中的巧用
有些繁难的数学计算,可以引入参数,直观地体现几个数之间的数量关系,再用等式的恒等变形的有关技巧消元,化难为易。
二、明确哪个量为参量,并对参量进行讨论或求参量的取值范围
1.方程(组)中参数取值的不确定性,引发对参数的讨论。
一般来说初中阶段提及的整式方程或分式方程中出现的未知数以字母表现,而其他字母都看成常数(即参数)。
分析:把x看成未知数,m看成参数,把方程的两个解用含参数m的代数式表示,再求解。
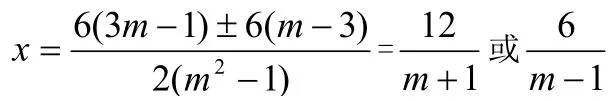
2.多元方程组中,先确定主元,再确定参数,把主元用参数的形式表示。
3.不等式(组)参数的取值范围如何确定?
1)根据不等式的性质解题。当不等式左右两边同除以一个正数时,不等号的方向不变;当不等式左右两边同除以一个负数时,不等号的方向改变。故含参数的一元一次不等式常要讨论求解。
2)根据不等式组的求解方法求解。不等式组求解集的法则是:同大取大;同小取小;小大,大小中间找;大大,小小无处找(无解)。若其中一个不等式含有参数,则可根据未知数的解集,求参数的取值范围。
三、用待定系数法求参数的值
四、参数的取值范围对函数最值的影响
当函数解析式确定时,自变量的取值范围会影响到函数图象。同样的函数解析式,值域就受定义域的影响。尤其是二次函数的区间最值问题、一元二次方程根的分布问题,对初中生来说很有挑战性。
分析:对称轴直线 1=x 确定,区间会变。由二次函数的增减性知:
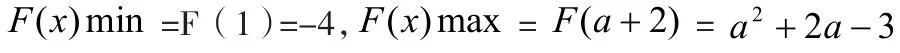
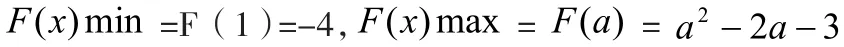
一般来说,函数区间最值问题的解决模式是:(1)从实际问题,合理引进参量;(2)由提供的基本模型和初始条件去确定函数关系式;(3)根据题意确定参量的取值范围;(4)画出区间函数的图象,数形结合并利用函数的增减性(单调性)求出最值。当然在二次函数的最值问题中,还有“轴变区间定”,“轴变区间变”等类型。而在解决一元二次方程根的问题上,常用到根与系数的关系、根的判别式求参数的范围。
五、几何问题代数化中参数的应用.
几何不在于做题多而在于把经典题题做熟,做透,吃透思路的形成过程。在某些纯几何背景的题目中,为了解决一些几何元素(线段、角、面积等)的关系,需要引入合适的量做为参数,用代数的语言描述几何要素之间的关系,再通过处理代数问题与分析代数结果的几何含义,最终解决几何问题。
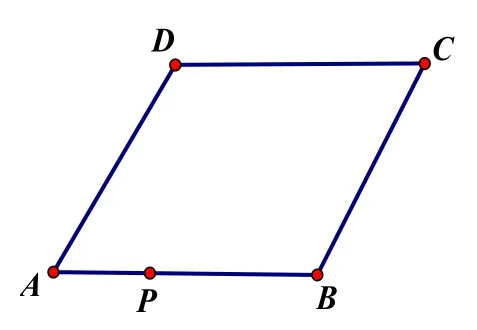
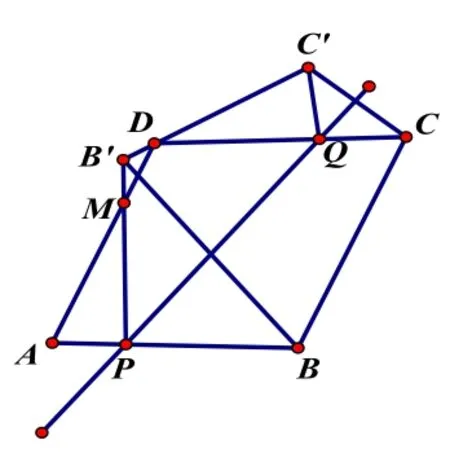
例3:在菱形ABCD中,点P在AB边上,
(1)以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B'、C'上,且B'、C'经过点D,折痕与四边形的另一交点为Q,请你作出四边形

图①
图②
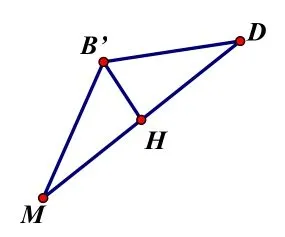
图③
由于点P是运动的点,故可设参数PA =a,PB=b,在解题中将其他动线段用a与b的代数式表示。

总之,含有参数的问题几乎覆盖了方程、函数,不等式、三角函数,数列、几何等初中数学的所有知识点,也涉及到一些重要的数学思想方法。在解决含有参数的问题时,常把许多相关的量放在同一个含参方程(组)下,再进行简化与运算。当然,应弄清对参数讨论的原因,并且在分类讨论时做到不遗不漏。对于隐含在动念几何中的含参数问题(几何中的定值问题、数量关系的证明题),适当引入参数,由几何性质与数形结合的思想解决更简洁有效。在今后的数学学习中一些绝对不等式的成立的条件往往用参数的集合的形式加以表示;函数的导数值主要是受参数的范围的影响;多个参数的互相制约也会产生。所以在初中数学应抓好以上几点参数问题的教学,让学生从“变”中找规律,“举一反三”,形成数学思维的阶梯式上升。
[1] 仇海宁.《中学数学竞赛中的参数问题》 2011第39期《考试周刊》之题型研究
[2] 张国良.《例说参数取值范围的求法》 [J].《中学数学研究》2009年第3期
[3] 汪祖享 康士凯.《代数问题几何化的几种途径》 1986年07期《教学与研究》
[4] 戴向阳.《 关于高中数学中参数问题的求解策略》 2011年第9期 《科学咨询:下旬》
曾立萱,1976年10月,现在泉州七中初中部任教,福建省三明地区永安市,已评为高级教师,研究方向:初中数学教育。
