基于PFC2D的复杂地层中振冲碎石桩成孔效应研究
2016-11-25唐珍
唐 珍
(四川蜀渝石油建筑安装工程有限责任公司,四川 成都 610081)
基于PFC2D的复杂地层中振冲碎石桩成孔效应研究
唐 珍
(四川蜀渝石油建筑安装工程有限责任公司,四川 成都 610081)
介绍了PFC数值模拟的原理,采用二维颗粒离散元法PFC2D,对复杂地层中振动碎石桩的成孔过程进行了数值模拟,并分析了不同夹砂层厚度及密实度对振动碎石桩成孔过程的影响,最终得出了一些有意义的结论。
离散单元法,PFC数值模拟,振冲碎石桩,成孔效应
传统的振冲碎石桩,是利用起重机吊起振冲器强烈水平振动和高压力水冲贯入到土层预定深度,形成钻孔,经过清孔后从地面向孔中逐段填入碎石,并利用振冲器产生水平向振动力振挤填料及周围土体,从而在地基中形成一根密实的桩柱体,和原基地土形成复合地基,并通过桩体与桩周土相互作用共同承担上部荷载从而达到提高地基承载力,减少沉降量,提高抗震液化能力,增加地基稳定性以及消除湿陷性黄土的湿陷性等作用。
松散及稍密的土层中,振冲器造孔容易,但由于土层相对松散,容易发生塌孔现象。密实及较硬的土层中,振冲器造孔比较困难,成孔的桩径小。地层的复杂多变对振冲器造孔进度造成极大影响,尤其是在圆砾含粉细砂夹层和中粗砂含粉砂夹层,常会出现“抱管”“串孔”等现场,严重影响施工进度,增大振冲器及配套设备损坏率。
本文通过PFC2D来数值模拟振冲碎石桩在复杂地层中的成孔效应。
1 PFC数值模拟原理
离散单元法是从20世纪70年代初开始兴起的一种数值计算方法,本方法的基本原理是基于牛顿第二定律基础建立起来的,它明显的优点在于可模拟离散块体系统及离散颗粒组合体系,适合解决非连续介质的断裂、破损及大变形问题。经过几十年的探索,离散单元法得到长足发展,不仅应用于边坡、矿山、隧道的稳定性研究及颗粒介质微细观结构分析中,还拓展到地震荷载、爆炸荷载以及地下水渗流、热传导、多场耦合等研究领域[1]。
1.1 PFC求解基本原理
PFC离散单元法是将整个物体分成许多微小单元,对每个单元进行分别求解,在求解过程中,不用满足几何连续性假设,单元之间颗粒接触与分离是通过力和位移的关系求出单元之间的相互作用力,再通过单元所受到的不平衡力和不平衡力矩确定单元的运动。离散单元法恰恰适合砂卵石土这种类型的非均质和大变形非连续结构问题的求解。
1.2 材料本构模型
PFC颗粒离散元法中提供了三种现成的本构模型:接触刚度模型、接触粘结模型和平行粘结模型。接触刚度模型适用于对散体材料的力学性能进行数值模拟,如大豆、谷物、碎石等;平行粘结模型在两个相互接触的颗粒之间设置了一种特殊的粘结键,使得两个相互接触的颗粒之间可以承受一定的作用力和力矩作用,适用于一些复合材料和胶结材料的数值模拟分析,如混凝土、钢材、岩石等;接触粘结模型是介于接触刚度模型和平行粘结模型中的一种模型,相互接触的颗粒之间存在一定的粘结力,可以承受一定范围的作用力,但是不能承受力矩的作用,适用于模拟具有一定粘结力的材料的数值模拟分析,如粘性土等。根据需要模拟的材料性质的不同,选用不同的本构模型是必要的。对于此次需要研究的对象为碎石,选取的本构模型为接触刚度模型。
2 振冲碎石桩成孔效应研究PFC建模
2.1 PFC模拟方案的选用
模拟方案以工程中复杂地层——黏土“夹砂”层为背景,运用离散元PFC软件模拟复杂地层中大功率振冲碎石桩的成孔机理及其影响因素。
地层分布选用粉质黏土层—粉砂层—中粗砂层,其中粉质黏土层厚4 m,粉砂层厚2 m,中粗砂层厚5 m。
由于中粗砂层中砂颗粒的粒径在1.6 mm~5 mm范围内,粉砂层和粉质黏土层中砂颗粒的粒径在0.075 mm~1.6 mm范围内,在颗粒离散元法中建立的颗粒单元的数量太大,数十万至百万,计算设备没法运行。根据计算设备的配置,以及粉砂层与中粗砂层的厚度关系,采用二维颗粒离散元法建立粉砂层和中粗砂层的离散元模型。
2.2 PFC建模思路
对振动碎石桩的成孔技术的研究采用二维颗粒离散元法(PFC2D)建立地层和振冲器的数值模型,通过模拟不同工况下,振冲器作用于土层的过程,分析振动碎石桩成孔过程中的影响因素。
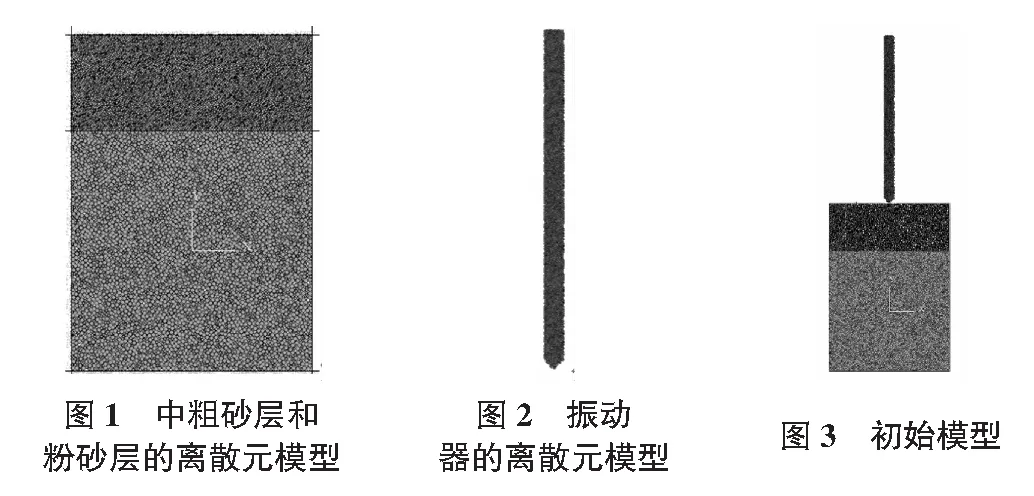
为了提高计算效率,在离散元建模的过程中,粉砂层和中粗砂层的厚度被缩小了10倍,粉质黏土层对粉砂层和中粗砂层的作用近似考虑成均布荷载的作用,经计算,该均布荷载取值为0.1 MPa。图1是在二维颗粒离散元法中建立的粉砂层和中粗砂层的数值模型,模型的宽度为0.5 m,中粗砂层的厚度为0.5 m,粉砂层的厚度为0.2 m。模型中总的颗粒数为12 213,其中中粗砂的颗粒数量为5 489,粒径在2 mm~5 mm之间;粉砂的颗粒数量为6 724,粒径在1 mm~2 mm之间。中粗砂和粉砂的离散元细观力学参数见表1。

表1 砂的颗粒离散元细观力学参数
振动器的离散元模型见图2,通过离散元法中clump logic的控制,可以将聚集在一起的有限数量的颗粒设置成一个超单元,超单元具有不变形的边界条件,用这样的超单元来模拟振动器是很合适的。
2.3 复杂地层中振冲碎石桩成孔效应分析
在振动碎石桩对复杂地层中成孔技术的研究中,主要考虑两个因素对振动碎石桩成孔的影响,即夹砂层的厚度变化和夹砂层的密实度变化对成孔的影响。
振冲碎石桩是地基处理的一种形式,它是利用一个产生水平向振动的管状设备在高压水流下边振边冲,在软弱地基上成孔,再在孔内分批填入碎石等坚硬材料制成一根根桩体,桩体和原来的地基构成复合地基,这样的复合地基同原来地基相比,承载力提高了,也减少了地基的沉降量,并且这种粗大的桩体具有排水和置换功能,能有效地消散地震等震动引起的超静孔隙水压力,有效减少砂土地基的液化现象[2,3]。
振动碎石桩的施工原理:利用起重机吊起振冲器,强烈的水平振动和高压力水冲贯入到土层预定的深度,形成钻孔。振冲器的偏心质量以及其偏心距是振冲器强烈水平振动的主要来源,为了能在离散元数值模拟中体现这种强烈振动,数值模拟的过程中,在振冲器的水平方向施加一个正弦波的速度,正弦波的频率尽可能与真实频率接近,正弦波的振幅不宜太大,以免振冲器开孔的偏差大于施工的要求;振冲器竖直方向的高压水冲是振冲器成孔的主要动力,数值模拟中对水冲的模拟涉及到流固耦合的运用,限于知识面的不足,数值模拟中将高压水冲的动力简化为一个恒定的速度。
振冲器在水平的正弦波速度和竖直的恒定速度下,匀速作用于土层,初始模型见图3,振冲器不同下降高度见图4~图10(其中,图4a)~图10a)为振冲器与土层的相对位置,图4b)~图10b)为振冲器附近颗粒的运动情况)。
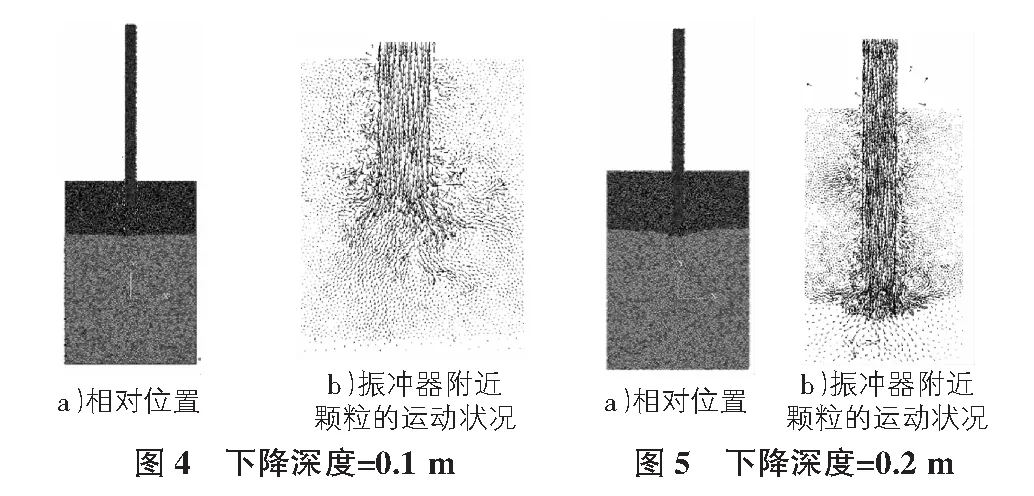
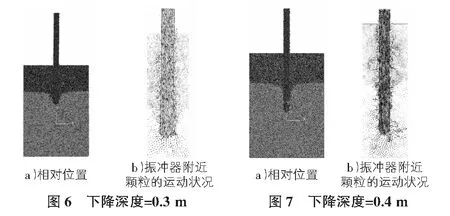
由于夹砂层的土体颗粒粒径比较小,在振冲器成孔的过程中,振冲器附近的土体颗粒与水作用将形成与水泥砂浆类似的混合物,此类混合物容易包裹、覆盖在振冲器的外表面,从而严重影响振冲器的成孔过程。其次,由于水和土体颗粒的共同作用,涉及到流固耦合的求解,流固耦合本身就是一个非常复杂的过程,由于流固耦合本身的近似程度很大,当前软件对流固耦合的数值模拟都存在很大的不足。
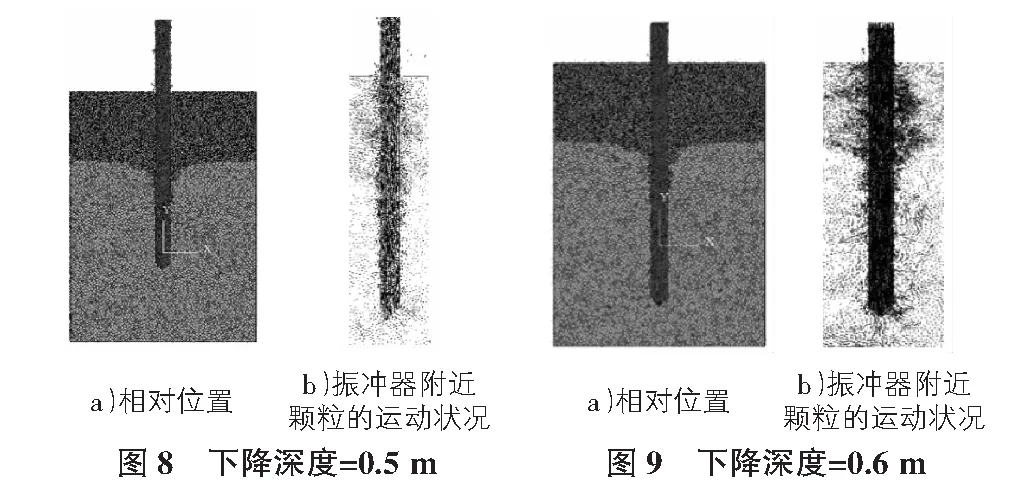

为了能够模拟夹砂层与振冲器的相互作用,并分析不同夹砂层对振冲器成孔的影响,数值模拟中将夹砂层内土体颗粒的摩擦系数调大一些,在振冲器成孔的过程中记录振冲器竖直方向上的受力变化,通过受力的变化反映不同夹砂层厚度对振冲器成孔的影响。下面主要分析不同夹砂层厚度以及不同夹砂层密实度对振冲器成孔的影响。
2.3.1 夹砂层不同厚度对桩体成孔的影响
为了研究不同夹砂层厚度对振动碎石桩成孔的影响,维持其余参数的恒定,改变夹砂层的厚度。数值模拟中中粗砂层的厚度恒定为0.5 m,粉砂层的厚度d取值分别为0.1 m,0.15 m,0.2 m,0.25 m,建立的中粗砂层和粉砂层的离散元模型与图1类似。
记录数值模拟中不同时刻振冲器的竖向受力,通过振冲器竖向受力的变化来间接反映夹砂层厚度对振动碎石桩成孔的影响。图11是夹砂层厚度不同时振冲器的成孔深度与振冲器竖向受力的关系曲线。
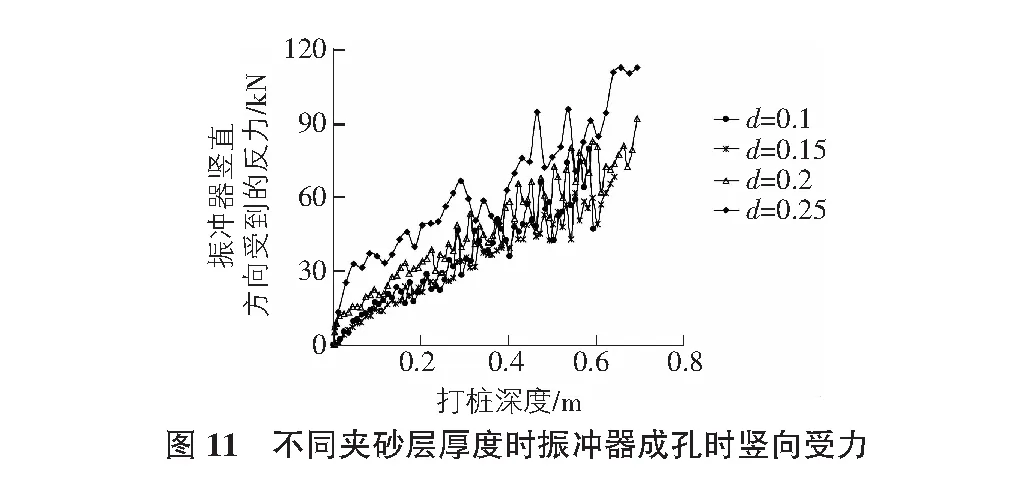
从图11可以看出,随着夹砂层厚度的增加,振冲器在成孔的过程中受到来自土层的作用力越大,当夹砂层的厚度从0.1 m增加至0.15 m时,振冲器在成孔的过程中受到的阻力几乎相差不大,即夹砂层的厚度改变对整个成孔基本没有影响;当夹砂层的厚度增加至0.2 m,0.25 m时,振冲器在成孔过程中的受力明显增加,即夹砂层在成孔的过程中所起的作用越来越明显。
2.3.2 夹砂层不同相对密实度对桩体成孔的影响
为了研究不同夹砂层相对密实度对振动碎石桩成孔的影响,在其余条件保持不变情况下,改变夹砂层的密实度。数值模拟中中粗砂层的厚度恒定为0.5 m,粉砂层厚度维持为0.2 m,粉砂层的相对密实度可以通过其孔隙比反映,孔隙比e取值分别为0.60,0.65,0.70,0.75,建立的中粗砂层和粉砂层的离散元模型如图1所示。
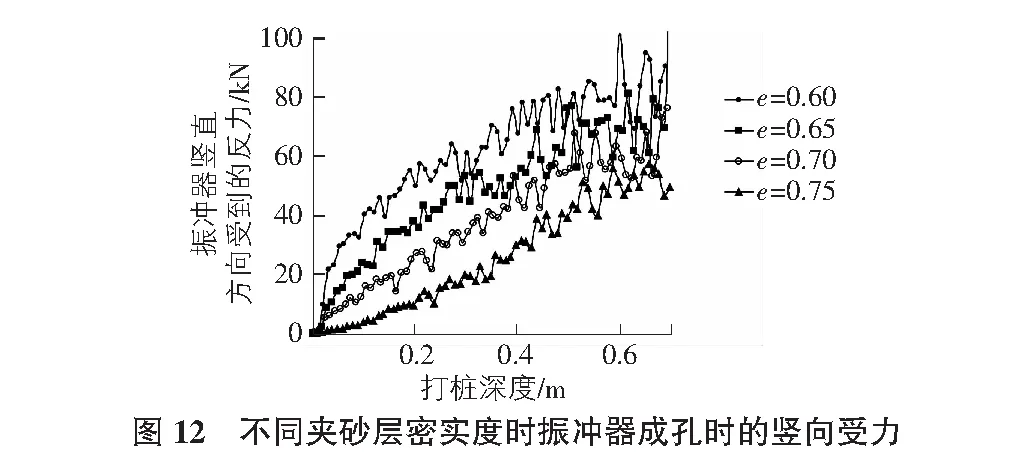
数值模拟中记录不同时刻振冲器下降的高度与振冲器竖直方向反力,描绘出不同夹砂层孔隙比时振冲器下降高度与振冲器竖直方向反力的关系曲线如图12所示。从图12可以看出,振冲器下降高度在0.2 m以内(基于粉砂层的厚度),夹砂层的孔隙比越小,即夹砂层的相对密实度越高,振冲器在该高度范围内受到的竖向反力越大,振冲器竖直方向反力的增加值与孔隙比的减小值近似呈线性增长的关系;夹砂层的孔隙比越小,振冲器在整个成孔的过程中竖向反力越大。在数值模拟中,振冲器也是由有限数量的颗粒组成,振冲器与土颗粒之间的作用其实就是颗粒与颗粒之间的作用,当以一定的速度挤压两个相互接触的颗粒时,颗粒之间的相互作用力会逐渐增加,直至两个颗粒发生相对滑移或者错动,颗粒之间的相互作用力就会急剧降低,所以图12中振冲
器的受力曲线的波动性较大,呈现一定的锯齿形上升趋势。
实际工程中,振冲器在向下运动成孔的过程中,振冲器的竖向力近似恒定,下降的速度是主要的变量;然而在数值模拟中,振冲器下降的速度是恒定的,振冲器的竖向受力是变量。故数值模拟与实际存在一定的差异,所以图12中所示不同夹砂层密实度对振动碎石桩成孔的影响只是定性的分析,而并非定量的分析。
3 结语
1)在夹砂层密实度一定,当夹砂层的厚度在某一个范围内变动时,夹砂层的厚度对振动碎石桩成孔的影响几乎没有太大的变化;当夹砂层的厚度超过某一个临界值时,夹砂层土颗粒与振冲器的相对作用明显增强,振冲器穿过夹砂层所需要的能量也越高,以致出现振冲器抱死等现象。
2)在夹砂层厚度一定,夹砂层土的孔隙比减小,土体的密实度上升,振冲器穿过夹砂层所需要的能量越高,能量消耗的增加值与夹砂层孔隙比的减小值呈线性增加的趋势。
[1] 王立慧.基于PFC的桩承式路堤土拱效应研究[D].西安:西安建筑科技大学,2013.
[2] 地基处理手册编写委员会.地基处理手册[M].北京:中国建筑工业出版社,2000.
[3] 高加成,刘恒武.碎石桩—强夯联合法加固湖区填土地基[J].湖南科技大学学报(自然科学版),2005,20(1):49-51.
Study on the drilling effect of vibro replacement stone piles in the complex formation based on PFC2D
Tang Zhen
(SichuanShuyuPetroleumBuildingInstallationEngineeringCo.,Ltd,Chengdu610081,China)
This paper introduces the principle of PFC numerical simulation, study on the drilling effect of vibro replacement stone piles in the complex formation based on the two-dimensional particle discrete element method PFC2D, and analyze the influence of different thickness and compactness of sand layer on the drilling process of vibro replacement stone piles, some significant conclusions are obtained.
discrete element method, PFC numerical simulation, vibro replacement stone piles, drilling effect
1009-6825(2016)28-0086-03
2016-07-29
唐 珍(1959- ),男,工程师
TU472.35
A
