基于粒子群优化BP神经网络的水产养殖水温及pH预测模型

徐大明， 周 超， 孙传恒， 杜永贵

(1 国家农业信息化工程技术研究中心，农业部农业信息技术重点实验室，北京市农业物联网工程技术研究中心，北京 100000;2 太原理工大学信息工程学院，山西 太原 030000)



基于粒子群优化BP神经网络的水产养殖水温及pH预测模型

徐大明1,2， 周 超1， 孙传恒1， 杜永贵2

(1 国家农业信息化工程技术研究中心，农业部农业信息技术重点实验室，北京市农业物联网工程技术研究中心，北京 100000;2 太原理工大学信息工程学院，山西 太原 030000)

针对养殖水质、水温及pH预测准确性低的问题，提出了一种基于粒子群优化BP神经网络的养殖水质参数预测方法。首先应用粒子群算法优化得出BP神经网络的初始权值和阈值，然后对得到的数据进行预处理，修复异常数据信息，再以当前时间的多个水质参数作为输入，下个时间点的水温、pH作为输出，建立养殖水质预测模型，最后利用采集的水质数据在BP神经网络中进行训练，并通过实验检验水质预测模型的可行性和预测性能。与支持向量回归(SVR)和传统BP神经网络相比，基于粒子群优化的BP神经网络在预测水温方面，均方根误差(RMSE)下降幅度分别为64.4%和86.7%；在预测pH方面，RMSE下降幅度分别为11.1%和78.9%。研究表明，基于粒子群优化的BP神经网络养殖水质预测模型具有灵活简便、预测精度高、易于实现的特点，同时具有很好的预测能力。

粒子群算法；BP神经网络；水产养殖；渔情预警；水质预测模型

随着物联网的发展，信息技术以其直观、快速、准确的特点，在水产养殖方面应用越来越广泛。因此，利用现代化信息技术对集约化养殖水质进行预测是十分必要和成熟的[1-3]。目前水产养殖水质预测系统是一个开放复杂的非线性、多参数、大时延的系统[4-5]，利用传统的数学方法很难准确构建水质模型。常用水质预测方法有水质模拟法、专家评估法、历史平均法、回归分析法等，这些方法对于模糊不确定性的养殖水质的预测精度，效果不甚理想[6-7]。

人工神经网络[8-10]具有非常强的自适应学习能力和对非线性函数的逼近能力，常被作为挖掘数据关系、构建预测模型的有力工具。国内学者在水质预测方面有大量的研究，如：构建了基于优化支持向量机的河蟹养殖水质预测模型，利用优化算法改进最小二乘支持向量机挖掘时间序列上的水质参数之间的关系[11-12]；提出了基于贝叶斯网络的海水养殖水质预测方法，解决了用间断采集数据预测连续水质参数的问题[13]；将模糊集理论中级别特征值的概念引入马尔可夫模型，提出一种基于投影距离的方法, 使之能够用于水质的定量预测[14]。这些研究都取得了非常好的预测效果。

但是，机器学习的方法依据大量准确的数据，经常由于传感器的采集传输故障或者其它客观因素的影响，约有1.2%的数据有明显的异常[15]。这些异常数据对模型的准确性和鲁棒性都有较大的影响，如何对这些异常数据进行处理目前还没有相关研究。本研究选用BP神经网络来构建养殖水质预测模型，利用粒子群算法优化其训练时间长、易陷入局部极值的缺陷，对采集到的异常数据进行处理，并以水产养殖中重要的参数(水温和pH)作为预测实例，考察模型的预测精度。

1 数据来源及方法

1.1 数据采集

采用的测试数据来自北京小汤山国家精准农业示范基地水质监测系统。该系统配备YSI6600多参数水质检测仪传感器，其技术指标有水温(WT)、pH、溶氧(DO)、电导率(EC)、分子氨含量(NH3-N)、离子氨含量(NH4+-N)。数据采集从2015年4月6日—4月12日，共7 d。系统的采样周期为5 min，鉴于每个周期内的数据变化不大，因此选择每隔15 min的数据作为有效值。样本总数为672组。将这些数据分成2部分，前572组数据作为学习样本，供水温及pH预测模型建模训练；后100组数据作为测试数据，用来检测水质预测模型的预测性能。部分原始数据见表1。

表1 部分实验样本原始数据

1.2 数据预处理

在采集的数据中，不同水质参数的单位不同，有些数据取值较大，这将导致神经网络收敛慢、训练时间长。为了消除这一现象对算法的影响，用下面的公式将数据标准化，将所有的数据归一化到区间[0.02，0.98]。

(1)

式中：x—原始数据；xmax、xmin—数据集的最大值和最小值。

1.3 粒子群算法

粒子群算法(Particle Swarm Optimization, PSO)[16-18]是一种源于模拟鸟群觅食行为的生物进化算法。在PSO中，对于优化问题的每一个候选解都是搜索空间上的一个点，称之为“粒子”。每一个粒子都有一个被目标函数决定的适应值，同时还有一个决定其飞翔方向和距离的速度，粒子们根据自身和当前的最优粒子位置在搜索空间中智能调整，直至满足要求为止。

粒子的速度和位置在迭代中的更新：

(2)

(3)

式中：ω—惯性权重，系保持原来速度的系数；c1、c2—粒子跟踪自己和整个群体最优值的权重系数；ξ、η—均匀分布在区间[0,1]内的随机数；r—约束因子。

1.4 传统BP神经网络

BP神经网络(Back Propagation neural network，BPNN)[19-21]属于典型的多层前馈神经网络，是目前应用最广泛的神经网络模型之一，包含输入层、隐含层和输出层。其学习过程由信号的正向传播和反向传播连个过程构成：在正向过程中，输入信号经过输入层，隐含层，经过网络的权值、阈值的作用后通过输出层输出，若输出值大于期望误差，则进行反向传播，如此反复。在反复的过程中，网络的权值和阈值都在进行自适应调整，直到所有的输出值都达到预定的误差，确定达到最小误差时相对应的网络参数(权值和阈值)，这就是BP神经网络的网络学习训练过程。经过训练的神经网络即能对类似的样本进行拟合，提供相关输入数据，神经网络将会按照训练好的网络参数计算输出数据。网络的输入和输出的关系如公式(4)、(5)所示：

(4)

yi=f(neti)

(5)

式中：xj—从上层神经元传来的输入信号;wij—从上层神经元j到神经元i的权值;θ—阈值，或称为偏置;neti—净激活;yi—神经元i的输出;f(x)—激活函数。激活函数对于收敛速度和拟合程度有显著的影响。

由于BP神经网络的初始权值和阈值是随机确定的，而它对初始权值和阈值又非常敏感，在多次迭代的过程中，易陷入局部最优解。以不同的权重初始化网络，其往往会收敛于不同的局部极值，造成了多次训练都会得到不同的结果。

1.5 基于PSO的BP神经网络优化

鉴于BP神经网络在具体运用中暴露出来的收敛时间长、易陷于局部最优解等缺点，本文利用PSO算法优化BP神经网络，来克服相关问题。具体步骤如下：

步骤1：初始化PSO算法的相关参数，包括种群数量、惯性权重、学习因子、最大迭代次数,以及位置和速度的取值范围。步骤2：根据输入输出信号的个数确定BP神经网络的拓扑结构，并初始化BP神经网络的权值、阈值的长度。步骤3：对BP神经网络的权值、阈值进行编码，得到PSO算法的初始种群。步骤4：运用PSO-BPNN对网络进行寻优迭代，计算每组粒子的适应度，根据初始粒子适应度值确定个体极值和群体极值，并将每个粒子的最好位置作为其历史最佳位置。步骤5：根据公式(2)和公式(3)，更新粒子的速度和位置。步骤6：判断是否满足结束条件，如果适应度值达到预设的精度，或者误差满足条件，或者达到最大迭代次数，则停止寻优迭代。此时粒子所处的位置就是要求的最优解，将其解码后作为BP神经网络的权值、阈值；如果不满足结束条件，回到步骤4。

优化算法的流程图如图1所示。

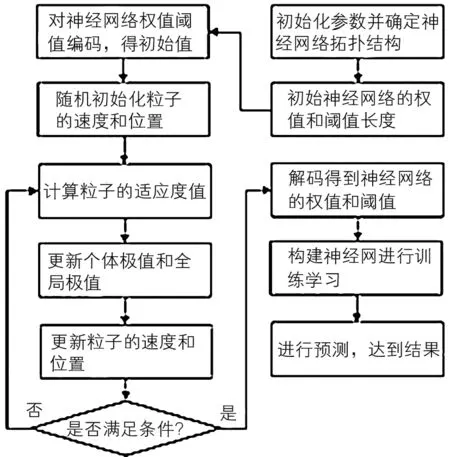
图1 PSO算法优化BP神经网络流程图Fig.1 Flow chart of BP neural network optimized by PSO

2 算法实现

2.1 基于PSO-BPNN的水产养殖预测模型的设计

对所建立的水质预测模型参数进行设置。

(1)粒子群算法部分。种群大小个数为20，权重系数c1=c2=2，约束因子r=0.729，迭代次数设置为200，惯性权重最大值ωmax=1.2，最小值ωmin=0.4，粒子的最大速度Vmax=5，最小速度Vmin=-1。适应度函数就采用BP神经网络的预测值和真实值之间的均方根误差(RMSE)。

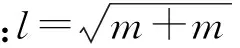
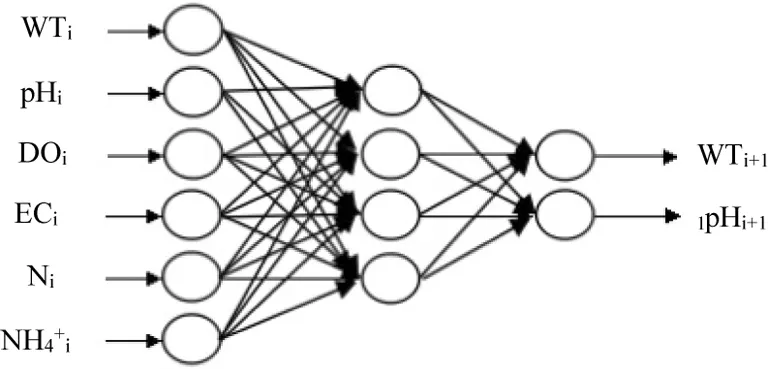
图2 BP神经网络拓扑结构Fig.2 Topological structure of BP neural network

2.2 基于PSO-BPNN的水产养殖预测模型设计

为了综合比较PSO-BPNN水质预测模型的性能，我们同时选取了传统的BP神经网络，支持向量回归(SVR)，同时进行预测。将实际值与预测值之间的均方根误差(RMSE)和决定系数(R2)作为判断模型性能的准则，均方根误差越小、决定系数越大，则模型的预测性能越好。计算公式如下：

(6)

(7)

3 结果

水质预测分为两个部分：

(1)筛选并修复原始水质数据中的异常数据组。将异常数据组的异常水质参数作为目标参数，其它水质参数作为输入参数，导入正常数据组在PSO-BPNN算法中进行学习，确定各参数之间的耦合关系；再将异常数据列的正常数据作为PSO-BPNN算法的输入参数，计算得出的值代替原本的异常数据。

(2)选取水产养殖中水温和pH作为预测目标。在PSO-BPNN预测模型中，将当前时间点的参数(WTi、pHi、DOi、ECi、NH3-Ni、NH4+-Ni)作为输入值，将下个时间点的WTi+1、pHi+1作为输出值，进行建模学习，然后将得到的预测结果与实际监测值进行比较分析。预测结果如图3所示。

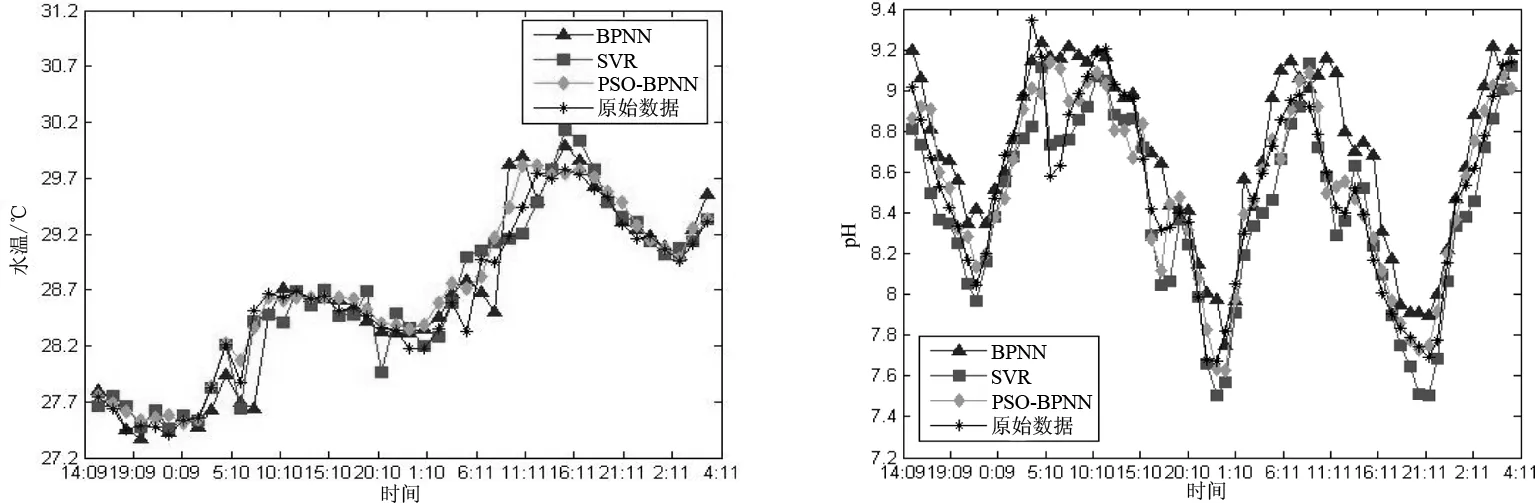
图3 预测结果对比图Fig.3 Comparison of the prediction results

表2列出了水温和pH在3种算法预测中的RMSE值。在水温预测中，PSO-BPNN的RMSE相比较SVR和BPNN，下降幅度分别达到64.4%和86.7%，R2分别提高了9.2%和17.2%；在pH预测中，PSO-BPNN的RMSE相比较SVR和BPNN，下降幅度分别达到11.1%和78.9%，R2分别提高了5.4%和14.0%。

同时，对三种不同方式处理异常数据的预测精度进行预测精度对比，从结果(表3)可以看出，PSO-BPNN水质预测模型的容错率较高，在删除异常数据组、保留异常数据的情况下，水温和pH预测依旧可以保持较高的准确性。当异常数据经过PSO-BPNN算法修复后，对比其他两种处理方式，水温和pH的RMSE分别下降11.2%、13.7%和72.2%、53.1%。

4 讨论

分析可知，(1)对于各项预测模型评价指标，本文提出的PSO-BPNN算法远远优于BP神经网

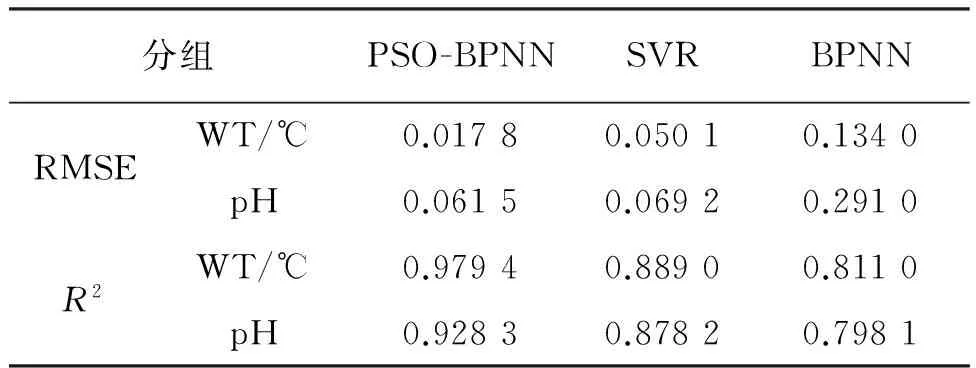
表2 3种水温及pH预测模型的均方根误差及决定系数

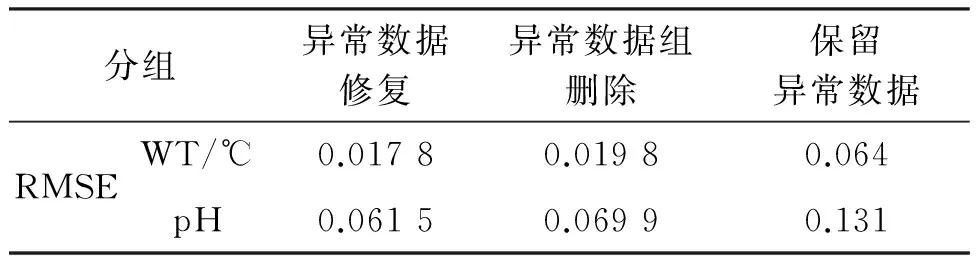
表3 3种水温及pH预测模型的均方根误差及决定系数

络算法，略优于支持向量回归算法，说明PSO-BPNN在养殖水温及pH预测运用上具有更好的泛化能力和预测精度。(2)在选取的2个预测参数中，3种算法对水温的预测结果都比pH的预测结果效果更好。参考相关文献[22]，这种情况是因为水温受到外界物理化学因素的影响较小，而pH往往受到外界的环境变化影响较大。(3)使用PSO-BPNN算法对异常数据进行修复处理后，预测模型的准确性大大提高，说明PSO-BPNN算法对包含异常数据的水质参数预测更加有效。

5 结论

水产养殖过程中，预测水温和pH对预防水质恶化及疾病爆发有着十分重要的现实意义和经济价值。本文介绍的一种基于粒子群优化的BP神经网络养殖水质预测模型，先用粒子群算法选择BP神经网络的初始权值和阈值，再将优化好的BP神经网络运用到水温和pH的预测。结果表明，PSO-BPNN水质预测模型对非线性时间序列上的养殖水质预测是可行的，相比于传统的BP神经网络和支持向量回归预测，具有更好的精度。同时，该算法还通过修复异常数据，提高了水质的预测精度。然而，在PSO-BPNN模型的训练过程中，对粒子群算法的参数选择目前还是依靠经验和拼凑法。因此，如何对粒子群算法的参数进行自适应调整是下一步研究的重要方向。

□

[1] HUANG G H, XIA J. Barries to sustainable water quality management[J].Journal of Environmental Management, 2001, 61(1)：1-23.

[2] 杨琛,白波,匡兴红.基于互联网的水产养殖环境智能监控系统[J].渔业现代化,2014,41(1)：35-39.

[3] 刘双印.基于计算智能的水产养殖水质预测预警方法研究[D].北京：中国农业大学,2014.

[4] 李道亮.物联网与智慧农业[J].渔业工程,2012(1)：35-39.

[5] 曾洋泱,匡迎春,沈岳,等.水产养殖水质监控技术研究现状及发展趋势[J].渔业现代化,2013,40(1)：40-44.

[6] 李如忠.水质预测模式理论研究进展与趋势分析[J].合肥大学学报,2006,29(1)：26-30.

[7] 王立,刘载文,吴成瑞.基于多元时序分析的水华预测及因素分析方法[J].化工学报,2013,64(12)：4649-4655.

[8] 薛鹏松,冯民权,邢肖鹏.基于马尔科夫链改进灰色神经网络的水质预测模型[J].武汉大学学报工学版,2012,45(3)：19-24.

[9] SHUANGYIN LIU, HAIJIANG TAI, QISHENG DING,etal. A hybrid approach of support vector regression with genetic algorithm optimization for aquaculture water quality prediction[J].Mathematical and Computer Modelling, 2013, 58(1)：458-465.

[10]杨柳,韩瑜,汪祖茂,等.基于BP神经网络的温榆河水质参数反演模型研究[J].水资源与水工程学报,2013,24(6)：25-28.

[11]李道亮,王剑秦,段青铃,等.集约化水产养殖数字化系统研究[J].中国科技成果,2008(2)：8-12.

[12]刘双印,徐龙琴,李振波,等.基于PCA_MCAFA_LSSVM的养殖水质pH值预测模型[J].农业机械学报,2014,45(5)：239-246.

[13]滕丽华,程利江,王海丽,等.象山港海水养殖区贝叶斯网络水质评价及预测[J].水土保持通报,2012,32(1)：189-191.

[14]岳遥,李天宏.基于模糊集理论的马尔可夫模型在水质定量预测中的应用[J].应用基础与工程科学学报,2011,19(2)：231-242.

[15]AYDILEK IB, ARSLAN A. A hybrid method for imputation of missing values using optimized fuzzy c-means with support vector regression and a genetic algorithm[J].Information Sciences, 2013, 233(2)：25-35.

[16]许兆美,刘永志,杨刚,等.粒子群优化BP神经网络的激光铣削质量预测模型[J].红外与激光工程,2013,42(9)：2370-2374.

[17]祁金秀,陈晶.基于粒子群算法优化的径向基函数水质预测模型[J].甘肃水利水电技术,2014,50(5)：1-5.

[18]刘伟,王建平,刘长虹,等.基于粒子群寻优的支持向量机番茄红素含量预测[J].农业机械学报,2012,43(4)：143-147.

[19]徐聪.数据挖掘方法在传统预测模型中的应用[J].河北工业科技,2009,26(4)：280-283.

[20]REN CHAO, AN NING, WANG JIANZHOU,etal. Optimal parameters selection for BP neural network based on particle swarm optimization：A case study of wind speed forecasting [J].Knowledge-Based Systems, 2014, 56：226-239.

[21]BAI TIECHENG, MENG HONGBING, YAO JIANGHE. A forecasting method of forest pests based on the rough set and PSO-BP neural network[J].Neural Computing and Applications, 2014, 25(7-8)：1699-1707.

[22]王锐刚.环境监测中水质指标间关系分析[J].能源环境保护,2011,25(6)：58-60.

Prediction model of aquaculture water temperature and pH based on BP neural network optimized by particle swarm algorithm

XU Daming1,2, ZHOU Chao1, SUN Chuanheng1, DU Yonggui2

(1 National Engineering Research Center for Information Technology in Agriculture， Key Laboratory of Agri-informatics, Ministry of Agriculture, Beijing Engineering Research Center of Agricultural Internet of Things, Beijing 100000,China 2 College of Information and Technology, Taiyuan University of Technology, Taiyuan 030000, China;)

Focused on the problem of inaccurate aquaculture water temperature and pH prediction, a mixed algorithm for water quality parameters prediction which was based on particle swarm optimization BP neural network (PSO-BPNN) was proposed. Firstly, the particle swarm optimization (PSO) algorithm was applied in calculating the initial weights and thresholds of BP neural network (BPNN).Secondly, the abnormal data were fixed andthe six parameters of water quality as inputs were used, the temperature and pH value of the next time point were used as outputs to establish aquaculture water quality prediction model. Finally, the collected water quality data were used to conduct training in BP neural network, and the feasibility and performance of water quality prediction model was tested through experiments. Compared with support vector regression (SVR) and normal BP neural network, in the aspect of predicting water temperature using PSO-BPNN, the decreasing amplitudes of RMSE were 64% and 80% respectively, while in the aspect of predicting pH value, the decreasing amplitudes of RMSE were 32% and 65% respectively. The results of experiments show that aquaculture water quality prediction model based on PSO-BPNN is flexible, simple, convenient and it also has a good capacity of prediction.

particle swarm optimization (PSO); BP neural network (BPNN); aquaculture; fishing condition warning; water quality prediction model

2015-09-28

2016-01-10

国家863计划项目(2012AA101905-02)；北京市自然科学基金资助项目(6152009)；国家现代农业产业技术体系建设专项 (CARS-49-03A)

徐大明(1991—)，男，硕士研究生，研究方向：算法优化，智能控制。E-mail：xudaming@vip.qq.com

孙传恒(1978—)，男，研究员，博士，研究方向：农业信息化。E-mail：sunch@nercita.org.cn

10.3969/j.issn.1007-9580.2016.01.005

TP181；S934

A

1007-9580(2016)01-024-06