地质统计反演在鄂尔多斯盆地南部彬长区块储层预测中的应用

袁春艳，贾家磊，张 红

(1.中国石化华北分公司 勘探开发研究院，河南 郑州 450007；2.潜能恒信能源技术股份有限公司，北京 100107)



地质统计反演在鄂尔多斯盆地南部彬长区块储层预测中的应用

袁春艳1，贾家磊1，张 红2

(1.中国石化华北分公司 勘探开发研究院，河南 郑州 450007；2.潜能恒信能源技术股份有限公司，北京 100107)

地质统计反演在储层薄、横向变化快的区域是一种比较实用的方法。地质统计学方法通过引入变差函数对已知观测值进行模拟，充分考虑空间数据的结构性和随机性。地质统计反演是将地质统计学与传统地震反演方法相结合的反演方法。它不仅可以提高反演的纵向分辨率，同时还可以实现更多储层参数的定量化反演。在鄂尔多斯盆地南部彬长区块储层进行实例应用，并利用该方法对纵向和横向非均质性强的薄储层且勘探程度较高的区域进行储层预测，取得了比传统地震反演更好的效果。

地质统计；地震反演；参数反演；储层预测

1 引 言

由于常规地震反演存在诸多不足，地质统计反演应运而生。地质统计反演(Geostatistical Inversion)由 Bortoli在1992年提出，1994年Haas、Dubrule[1]和Rothman[2]等又在SEG年会上对该方法进行了讨论，但受制于对计算机硬件要求和算法本身的复杂性，该方法推广较慢，近年来随着计算机技术的快速发展，该方法得到了越来越广泛的应用[3]。地质统计反演以地震反演为初始模型，从井点出发，井间遵从原始地震数据，建立定量的波阻抗三维地质模型,进行储层横向预测。充分发挥了地震资料横向上资料密集和测井资料纵向上分辨储层能力高的优势。因此，地质统计反演提高了纵向分辨率的同时，也利用地震资料降低了井间的不确定性，在研究储层的空间特征和厚度变化规律方面具有独特的优势。

2 方法原理

地质统计反演是以地质、地震和测井资料为基础，应用地质统计学方法和随机函数理论，并结合传统的地震反演技术，在每一个地震道(或多个地震道)产生多个可选的等概率的储层参数模型的一种地震反演方法。它主要包括变差函数分析、随机模拟和随机地震反演，其中变差函数分析是基础，随机模拟和随机地震反演是手段，两者的有机结合可以对非均质性强的薄储层进行有效预测[6]。

2.1 变差函数分析

通过引入变差函数对储层参数进行空间分布预测，能充分考虑数据的空间结构性和随机性。变差函数的表达式为：

(1)

即变差函数为区域化变量和两点之差的方差之半。其中，h为滞后距[4]。

变差函数一个很重要的特征值是它的变程，如图1所示。变程反映了区域化变量的空间相关性。对于某个随机变量，沿某一方向变程越大，表明该变量在该方向上变化越慢[10]。反演过程中，利用横向变程和纵向变程宏观描述地质目标体大小。横向变程的确定受井点的限制，当井点少、井点分布不规则的时候，用井资料求得的横向变程可信度较低，可以从约束稀疏脉冲反演得到的地质体的展布特征中拾取；而纵向变程则可以直接从测井资料中分析得到。

图1 变差函数示意图Fig.1 Variation function diagram

2.2 随机模拟

随机模拟是利用变差函数得到的空间数据场中数据之间的相互关系，建立起空间储层参数点之间的统计相关函数的过程。随机模拟运用序贯模拟的思想将空间某一位置待模拟节点的某邻域内所有已知值(包括原始测量值和先前已得到模拟值)作为模拟初始条件，对该节点进行模拟，把得到的模拟结果作为后续模拟的条件数据，继续进行下一节点的模拟[5]。

2.3 随机地震反演

随机地震反演是在地震数据约束下反复进行随机模拟的迭代过程，直到模拟结果与原始地震数据具有很好的匹配为止[6]。如果待反演的储层参数不是波阻抗，则需要分析其与波阻抗之间的相关性，根据这种相关性将该参数转换到波阻抗域，再进行以上反演过程。随机地震反演得到的结果是多个等概率的数据体，它们同时符合测井数据和地震数据的变化规律，并受建立的初始模型的约束。

3 应用实例

研究工区位于鄂尔多斯盆地南部彬长区块，主力油层为A1，油藏具有低渗透、低孔隙度的特性，属致密性油藏。且该工区构造-岩性圈闭的复合类型，属于隐蔽油气藏勘探，勘探难度较大；同时，工区砂体厚度普遍较薄，砂层内物性纵横向非均质性突出；工区内的深层地震数据信噪比和分辨率都比较低，不利于深层的储层预测与评价。因此，用传统的地震反演方法进行储层预测已经不能满足本工区勘探开发的要求，应选用具有高精度储层描述能力和能够对其他属性参数进行有效反演的地质统计反演方法对本工区进行储层预测和评价，其反演流程如图2所示。

其中约束稀疏脉冲反演、敏感参数分析与变差函数分析是反演过程中的核心部分。而测井资料预处理、层位标定与子波提取和初始模型的建立是整个反演工作的基础，也十分重要[7，8]。

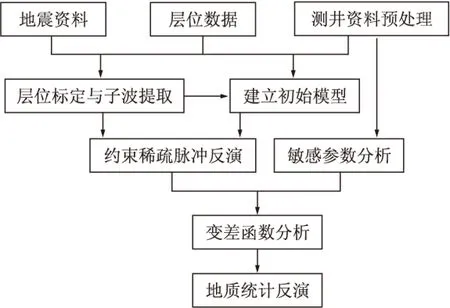
图2 地质统计反演流程Fig.2 Workflow of geostatistical inversion

3.1 约束稀疏脉冲反演

约束稀疏脉冲反演为地质统计反演提供储层横向上的变化趋势，其反演结果可以用来求取横向上的变差函数，是地质统计反演的基础。

在约束稀疏脉冲反演算法中，遵循以下原则:

最小目标函数为：Fmin=Lp(r)+λLq(s-d)其中：Fmin为目标函数，r为反射系数，Lp(r)用来确保稀疏性；λ控制原始地震记录与合成地震记录的匹配程度；d为原始地震记录，s为合成地震记录，Lq(s-d)用来确保与地震数据好的拟合性，这两项相互矛盾。低λ值强调稀疏性，约束稀疏脉冲反演结果分辨率低，残差较大；高λ值强调拟合性，使一些噪音加进了反演剖面中，同时由于忽略了反射系数的稀疏性，从而忽略了波阻抗变化的低频背景[3]。因此，寻找一个合适的λ值是做好约束稀疏脉冲反演的关键。通过反复试验，确定研究区λ值为20时，反演较好地兼顾了反射系数洗属性和地震数据拟合性。如图3所示，反演成果与井上波阻抗曲线较吻合，与地震数据吻合较好，为下步地质统计反演提供了较为可靠的横向变化趋势。

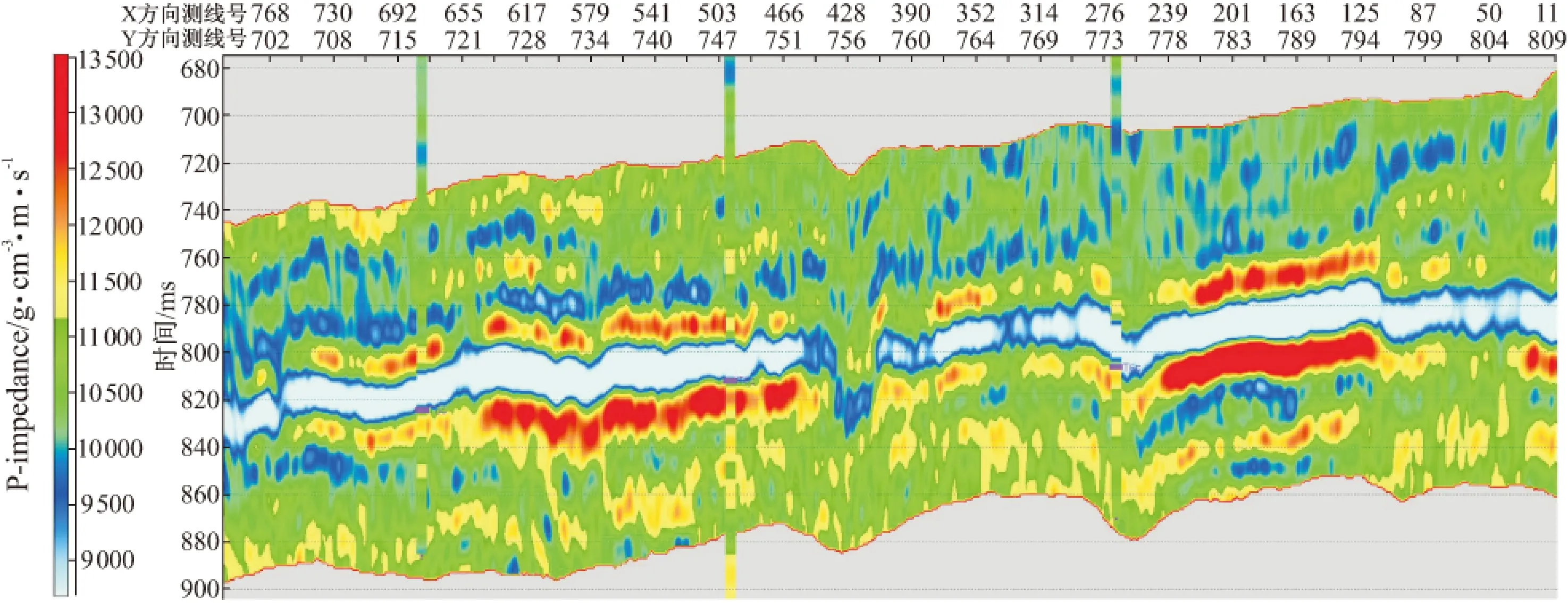
图3 约束稀疏脉冲反演波阻抗剖面Fig.3 The SSI impedance inversion profile

3.2 储层敏感参数分析

地质统计反演的优势之一是不仅能对波阻抗进行反演，还能对其他参数进行反演。如果储层敏感参数不是波阻抗，而是其他参数，当该参数与波阻抗有较好的相关性(0.7左右)时，利用地质统计反演能够对其进行有效的定量预测。

研究区利用储集层岩电曲线的直方图分析得到敏感参数。图4、图5分别是目的储层A1的砂泥岩波阻抗和伽马直方分布图，由图中可知：砂岩和泥岩的波阻抗值域范围重叠，不能有效区分；而砂岩和泥岩的伽马值具有较好的区分度，即伽马小于95 API时是砂岩，大于95 API时是泥岩。通过对伽马和波阻抗进行交汇分析可知，两者之间具有较好的相关性(约为0.6)。因此，可以选取地质统计学伽马反演对研究区砂岩进行预测。

3.3 变差函数分析

随机模拟是以数据的空间分布特征为基础对数据进行内插外推的过程，而数据的空间分布特征是用变差函数描述，所以变差函数分析至关重要。其中，纵向上的变程通过对工区内已知井的伽马曲线进行变差分析拾取，分别用不同的模型(高斯模型、指数模型或球状模型等)对样本点进行拟合分析，其中指数模型具有较好的拟合效果，拟合得到纵向上的变程为5.2 m(图6)。横向上的变程则通过量取地质体的大小来确定，在约束稀疏脉冲反演成果的基础上(图8)，根据地质体在平面上的分布特征，对不同大小的横向变程参数进行反演测试，最终确定2.5 km×2.5 km的横向变程测试效果最佳。

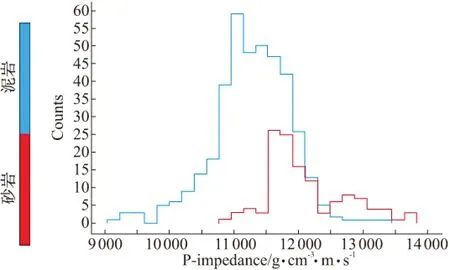
图4 波阻抗直方图Fig.4 Histogram of impedance

图5 伽马直方图Fig.5 Histogram of GR

利用分析得到的伽马变差函数对其进行随机模拟及随机反演得到多套伽马数据体，对不同数据体利用地质认识和实钻资料进行评价，优选出能够较好地反映工区储层分布特征的一套数据体。

图6 A1储层GR变差函数(纵向)Fig.6 The vertical variation function diagram of GR in A1 reservoir

4 效果分析

图7是目标区地质统计学伽马反演的一条成果剖面，相比约束稀疏脉冲反演结果(图3)，地质统计反演具有较高的垂向分辨能力，清晰地刻画出了薄层砂体的分布特征，且井点处反演结果与实钻测井完全吻合。

图9为目标区A1目的层地质统计学伽马反演提取的砂岩厚度平面图，图10为地质人员根据本工区的沉积环境和测井实钻情况勾画的A1目的层砂厚平面分布图。反演成果图与基于地质认识勾绘的砂厚图平面上砂岩展布特征一致，且井点处砂岩厚度一致。

通过对目标区地质统计伽马反演的剖面和平面成果进行评价，认为反演成果与地质认识一致、与实钻井资料一致，反演成果可靠，可用于该区薄储层预测。

在此基础上，目标区应用该预测成果进行了水平井井位部署。截至目前，新钻水平井共37口(图10)，砂体钻遇符合率为100%，37口井中有22口井获得高产油流，表明地质统计学反演技术对于该区平面非均质性强的薄储层具有较好的预测性。

图7 地质统计伽马反演剖面Fig.7 The geostatistics GR inversion profile

图8 波阻抗反演平面Fig.8 The plan of impedance inversion

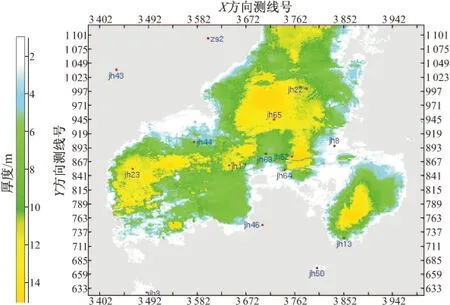
图9 地质统计GR反演平面Fig.9 The plan of geostatistics GR inversion

图10 地质砂体厚度Fig.10 Sand thickness of wells

5 结 语

由于研究区块目的储层横向非均质性强，且储层较薄，地震信噪比低、分辨率低，预测难度大，传统的地震反演技术不能满足储层预测要求；而地质统计反演能有效地综合地质、测井、地震资料，使反演结果的分辨率得到极大的提高，通过将地质统计学GR反演结果与实钻井的钻遇效果对比分析，认为该方法对于解决该区薄层的预测是有效的。但在预测过程中一定要做好基础数据(测井数据标准化、子波提取等)的准备工作，敏感参数及变差函数的选取要符合该区的地质特征。

[1]Dubrule O, Thibaut M， Lamy P H. Geostatistical reservoir aracterization constrained by 3D seismic data [J]. Petroleum Geoscience,1998(4):121-128.

[2]Rothman D H. Ceostatistical inversion of 3-D Seismic data for thin-sand delineation[J]. Geophysics,1998, 51(2):332-346.

[3]李方明.地质统计反演之随机地震反演方法——以苏M盆地P油田为例[J].石油勘探与开发，2007,34(4):451-455.

[4]王泽华,李庆.地质统计分析方法在储层预测中的应用[J].新疆石油学院院报,2001,13(1):26-29.

[5]慎国强,孟宪军,王玉梅,等.随机地震反演方法及其在埕北35井区的应用[J].石油地球物理勘探,2004,39(1):75-81.

[6]李方明,计智锋,赵国良,等.地质统计反演之随机地震反演方法——以苏丹M盆地P油田为例[J].石油勘探与开发,2007,34(4):451-455.

[7]龚伟,胡小菊,刘军,等.Jason反演在塔中顺西地区碳酸盐岩储层预测中的应用[J].工程地球物理学报,2014,11(5):593-594.

[8]孙均,杨飞,汪超,等.Jason与Strata联合反演技术在储层预测中的应用[J].工程地球物理学报,2010,7(3):293.

[9]张超英,周小鹰,董宁.测井约束的地震反演在鄂尔多斯盆地大牛地气田中的应用[J].地球物理学进展,2004,19(4):10-15.

[10]侯景儒,尹镇南.实用地质统计学[M].北京:石油工业出版社,1998：1-73.

The Application of Geological Statistics to Reservoir Prediction

Yuan Chunyan1，Jia Jialei1，Zhang Hong2

(1.ExplorationandDevelopmentResearchInstitute,NorthChinaBranchofSinopec,ZhengzhouHenan450007,China; 2.SinoGeophysicalCo.,Ltd.,Beijing100107,China)

Geological statistical inversion is a relative practical method in lateral changes rapidly and thin reservoir area. Geological statistical method refers to use variation function to simulate the known observations, which takes full consideration of the structure and randomness of spatial data. This new method integrated with conventional inversion methods can improve the vertical resolution and achieve the quantitative inversion of logging parameters. In this area, the layers are thinner and thinner, and the vertical and horizontal distributions are not even. In this case, Geological statistical inversion method is used to make the reservoir prediction and achieves results, which are better than the traditional seismic inversion.

geological statistics; seismic inversion; parameter inversion; reservoir prediction

1672—7940(2016)01—0077—05

10.3969/j.issn.1672-7940.2016.01.013

袁春艳(1986-)，女，助理工程师，主要从事地震资料综合解释工作。E-mail:y10205206@126.com

P631.4

A

2015-03-27