有限元地震数值模拟中无限元边界的应用

李 志， 薛霆虓,2,张海亮

(1.桂林理工大学 地球科学学院，广西 桂林 541004；2.桂林理工大学 广西地质工程中心区重点实验室，广西 桂林 541004；3.中化地质矿山总局 山东地质勘查院，山东 济南 250013)



有限元地震数值模拟中无限元边界的应用

李 志1， 薛霆虓1,2,张海亮3

(1.桂林理工大学 地球科学学院，广西 桂林 541004；2.桂林理工大学 广西地质工程中心区重点实验室，广西 桂林 541004；3.中化地质矿山总局 山东地质勘查院，山东 济南 250013)

在用有限元做地震数值模拟中，对于研究无限区域的问题，需要在模型的边界上采用一定的边界条件，其他方法设置边界条件较为困难，而利用无限元方法，可以比较有效地设计吸收边界，编程也较为方便。本文设计了一些简单的模型，利用有限元方法进行模拟，在边界处设计了无限元，并得到了地震快照和人工地震记录。分析对比结果可以明显地看出，在使用无限元的方法后模型边界的影响几乎被消除，且适用于复杂地形。在解决无限域的问题上使用无限元能更真实地模拟地震波传播过程。

地震数值模拟；有限元；无限元

1 引 言

地震数值模拟是地震勘探和地震学的重要基础。所谓地震数值模拟就是对实际的地质、 地球物理问题作适当的近似，形成简化的数学模型，采用数值计算方法获取地震响应的过程。地震数值模拟是了解地震波在地下介质中传播规律、帮助解释观测数据的有效手段[1]。这种地震数值模拟方法已在地震勘探和天然地震领域中得到广泛的应用。它不但在石油、天然气、煤、金属和非金属等矿产资源及工程和环境地球物理中得到普遍的应用，而且在地震灾害预测、地震区带划分以及地壳构造和地球内部结构研究中，也得到相当广泛的应用[2]。

地震数值模拟有多种方法，比如有限差分法、有限元法等等。其中，有限差分法编程相对简单，计算成本少，计算速度快，因此在地震勘探等领域得到了广泛的应用。但是有限差分法对复杂模型，比如地形起伏等情况，编程较为困难。有限元法虽然编程较为繁琐，计算成本较大，但是可以模拟复杂模型，比如有起伏地形的模型。有限元法也是地震数值模拟中的一种较好的方法。然而，在使用有限元方法过程中，只能通过建立有限域的模型来模拟无限域的地下介质，人为地引入介质边界，从而使得计算结果中出现无实际意义的边界强反射，严重地干扰了有效波信息，并影响了对地震波传播规律的正确认识[3]。为此，需要解决如何定义无限的区域，通常人为地截取足够大的区域进行有限元网格划分[4]，或者在模型的边界上采用一定的边界条件从而达到消减人为边界反射的目的[5]。

在有限差分方法中，目前使用广泛的两类吸收边界条件：海绵吸收边界条件和傍轴近似吸收边界条件。海绵吸收边界条件利用黏滞边界或靠近边界的条带范围内对入射波进行衰减[6,7]。Berenger[8]提出的理想匹配层法( PML method)是对海绵吸收边界条件的进一步改善。傍轴近似吸收边界条件基于单程波传播的方法原理，将不同近似条件下的单程波方程作为不同边界处的吸收边界条件[9-12]。在有限元中使用PML等方法相对较为复杂，编程也困难。

在有限元的模型边界中加入无限元，可以完美实现无限域的模拟且编程较为容易。1973年R Ungless[13]首先提出无限元的思想，此后Bettess[14]、Beer和Meek[15]、Zienkiewicz[16]等人发展了这种方法[17]。有限元和无限元耦合模型在求解实际问题方面有着广泛的实用性，在模拟无限域问题上有很大的优势[19-23]。

2 无限元的原理

用有限元和无限元相结合的方法求解问题时，除了要用一般的有限元构造近场的网格外，还需要用无限元构造远场网格。有限元与无限元之间存在分界点，通常可假设该分界点到无限处的位移是线性分布的，这个线性假设相当合理，该无限元网格对近场网格的影响的精度是足够的，为此我们需要构造无限元的统一形式的基本解u。

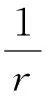
以一维问题为例，如图1中所示，设有限元和无限元的分界点为r1，奇异点位置为r0，r0到r1的距离为a，单位为m，r1作为分界点，位移为u1；r2为延伸到无限元中的一点，到分界点r1的距离为a，其位移为u2;r3作为无限远点，位移自然为0；将坐标进行如下转换。

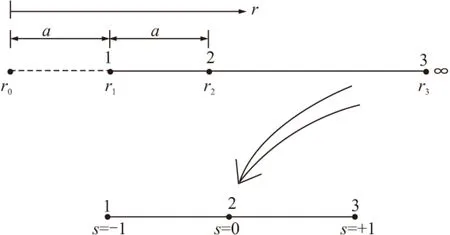
图1 无限元中的极点位置Fig.1 The pole position in infinite element

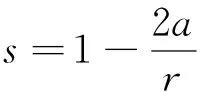
(1)

式中：s是映射坐标系的坐标；r是距离极点的距离。

在无限元中采用标准的二次位移插值函数：

(2)

或者写成

(3)

这样在1点，r=a,s=-1,u=u1；在2点，r=2a,s=0,u=u2；在3点，r=∞,s=1,u=0，说明构造的位移插值函数满足要求[19]。

3 算例分析

3.1 模型设计

本文选取的是二维弹性模型进行分析，有限元计算的区域范围是40 m×20 m，材料的杨氏模量为3×1010Pa，泊松比为0.2，密度2 500 kg/m3。本文中的3个算例都是在模型的坐标原点处加载一个震源，震源模型为雷克子波，波形图如图2所示。震源作用时长为2 ms，作用在原点左右1 m的范围上，振幅为500 000 Pa，如图3所示。本文分别就有限元模型和有限元与无限元耦合模型讨论在30 ms内各节点的位移和速度情况。

本文的模型中使用了0.5 m的网格和0.1 m的加密网格(在震源作用半径1 m的半圆中加密网格)。在有限元模型中共使用了4 511个四边形网格和142个三角形网格，如图4所示。在有限元和无限元耦合模型中共使用了4 581个四边形网格、128个三角形网格和160个无限单元网格，如图4、图5所示。为了更好地说明无限元的实用性，笔者还建立了一个有地形起伏的模型，使用了4 681个四边形网格、147个三角形网格和164个无限单元网格，如图6所示。

图2 雷克子波波形Fig.2 The chart of Ricker wavelet

图3 加载震源Fig.3 The figure of loading source

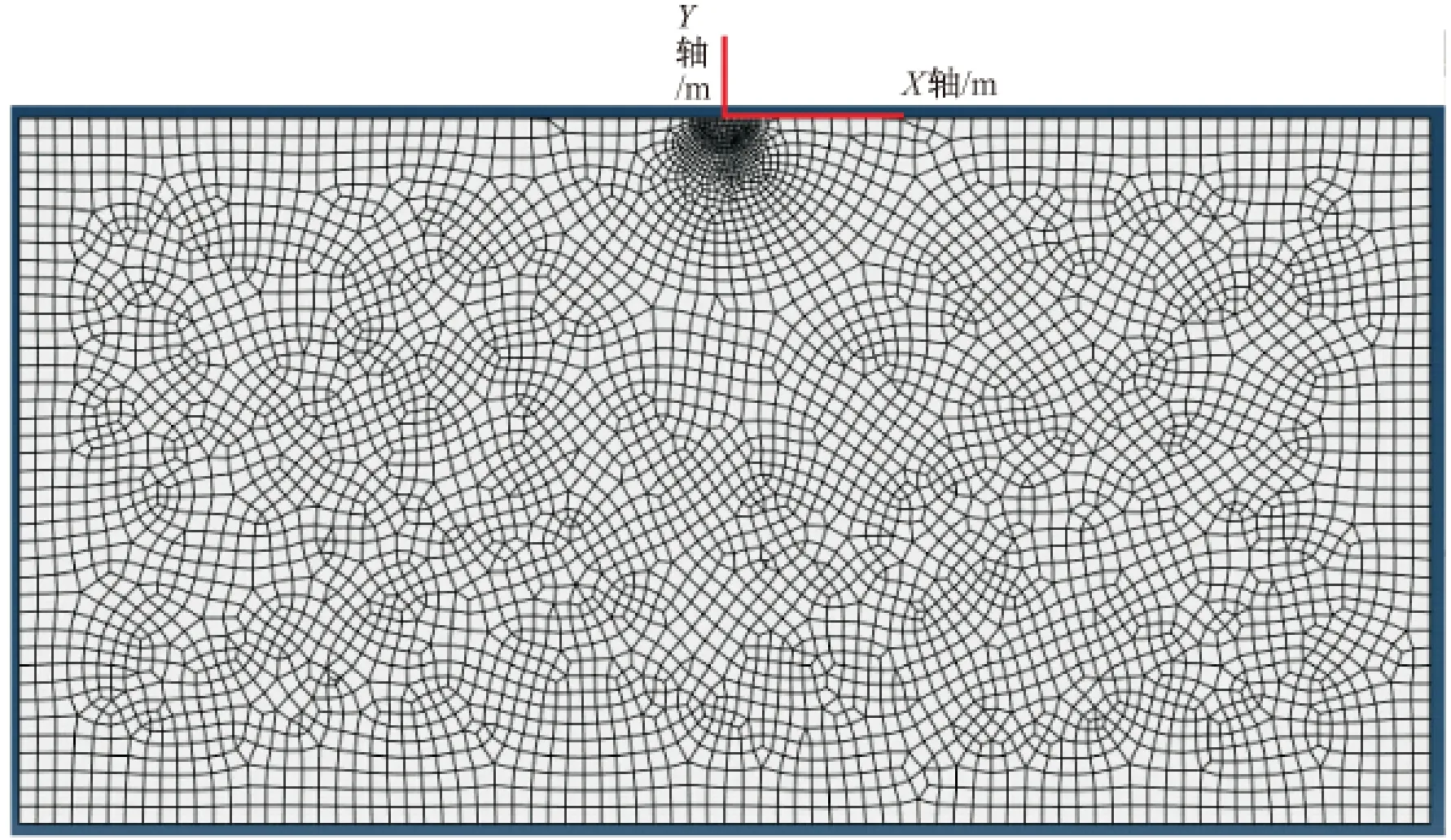
图4 模型的有限元网格Fig.4 The finite element mesh of the model

图5 模型的有限元和无限元耦合网格Fig.5 The model mesh with finite element and infinite element

图6 含地形的有限元和无限元耦合网格Fig.6 The terrain model mesh with finite element and infinite element

3.2 结果分析

对上述三种模型应用有限元软件做数值模拟计算，可以得到下面一系列图形，图7(a)～图7

(e)分别表示有限元网格的模型在时间为2 ms、4 ms、6 ms、8 ms和10 ms时模型位移场的场值。图8(a)～图8(e)分别表示有限元和无限元耦合网格的模型在时间为2 ms、4 ms、6 ms、8 ms和10 ms时模型位移场的场值。图9(a)～图9(e)分别表示含地形的有限元和无限元耦合网格的模型在时间为2 ms、4 ms、6 ms、8 ms和10 ms时模型位移场的场值。

图7(a)～图7(e)、图8(a)～图8(e)和图9(a)～图9(e)分别表示地震波向外传播的一个过程，但是由上述多幅图可以看出，在地震波还未传达到模型边界的时候，即在6 ms以前，三种模型的波形图完全一致。但在6 ms的时刻未使用无限元的模型，在地面明显出现了反射波，8 ms和10 ms的波形图更加明显，而使用了无限元的模型完全看不到模型边界所产生的反射波。对比图8(a)～图8(e)和图9(a)～图9(e)可以看出使用无限元对于含地形起伏的模型一样地适用。

图7 2 ms、4 ms、6 ms、8 ms和10 ms时位移场Fig.7 Displacement field in 2 ms, 4 ms, 6 ms, 8 ms and 10 ms

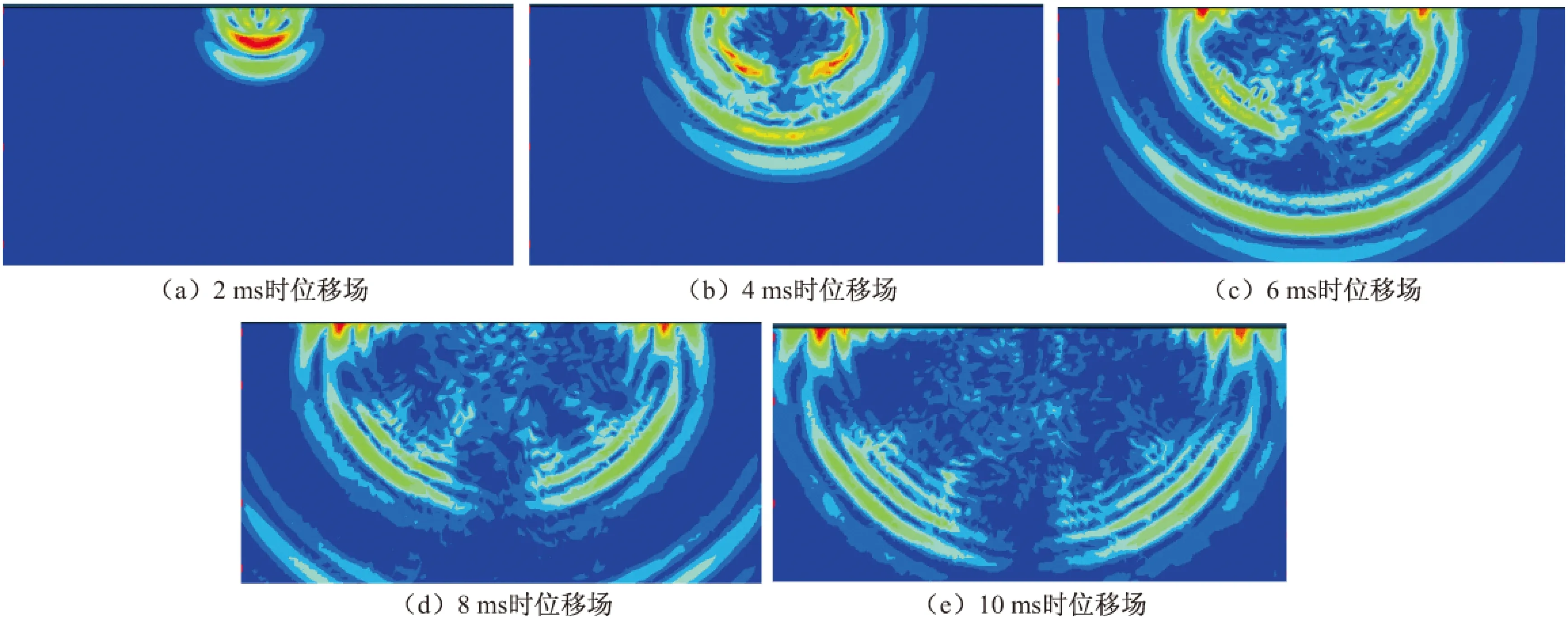
图8 2 ms、4 ms、6 ms、8 ms和10 ms时位移场Fig.8 Displacement field in 2 ms, 4 ms, 6 ms, 8 ms and 10 ms

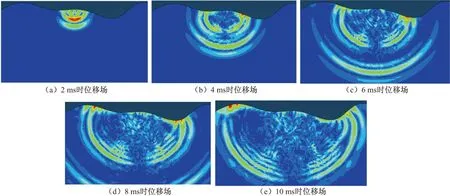
图9 2 ms、4 ms、6 ms、8 ms和10 ms时位移场Fig.9 Displacement field in 2 ms, 4 ms, 6 ms, 8 ms and 10 ms

为了更加清楚地对比这三种模型的差异，在地表每隔2m选取一个节点垂直方向上的位移随时间变化的数据，并运用GMT画图软件，画出20个节点的地震时间剖面图，纵坐标表示时间长度共0.03 s，如图10、图11和图12所示。

图10 有限元网格的地震时间剖面Fig.10 Seismic time profile of finite element mesh

图11 有限元与无限元耦合网格的地震时间剖面Fig.11 Seismic time profile of finite element and infinite element mesh

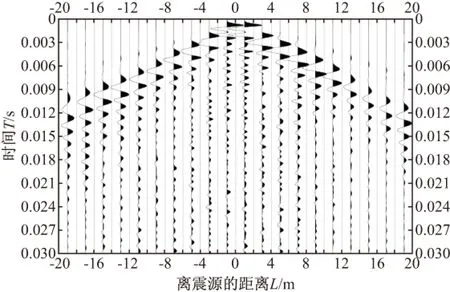
图12 含地形的无限元与有限元耦合网格的地震时间剖面Fig.12 Seismic time profile of the terrain model of finite element and infinite element mesh

图10与图11和图12对比而言可以清晰地看见底面的反射波，而图11和图12由于模型使用了无限元几乎看不到反射波，而且图12能看到地表地形起伏对初始波到来的时间的影响。

4 结 论

本文主要运用了有限元软件做了一个地震数值模拟，对有限元模型和有限元和无限元耦合模型做了详细的分析和讨论，对比了这三种模型的结果，可以得到一个明显的结论，在模拟无限域的问题上，使用无限元和有限元耦合模型可以很好地消除模型边界的反射，更加接近于真实情况。有限元和无限元的结合，既能模拟复杂介质，又能简便地设置吸收边界，达到模拟无限区域的目的。

[1]任志明,刘洋.一阶弹性波方程数值模拟中的混合吸收边界条件[J].地球物理学报,2014,57(2):595-606.

[2]牟永光,裴正林.三维复杂介质地震数值模拟[M].北京：石油工业出版社，2005:1-2.

[3]马在田.计算地球物理学概论[M].上海：同济大学出版社,1997:10-71.

[4]戚玉亮,大塚久哲.ABAQUS动力无限元人工边界研究[J].岩土力学,2014,35(10):3 007-3 012.

[5]夏凡,董良国,马在田.三维弹性波数值模拟中的吸收边界条件[J].地球物理学报,2004,47(1):132-136.

[6]Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J].Geophysics.1985,50(9):705-708.

[7]Kosloff D, Kosloff R. Absorbing boundaries for wave propagation problems[J].Computer.Phys., 1986,63(6):363-376.

[8]Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics.1994,114(7):185-200.

[9]Clayton R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America.1977,67(10):1 529-1 540.

[10]Higdon R L. Absorbing boundary conditions for elastic waves[J]. Geophysics.1991,56(2):231-241.

[11]Randall C J. Absorbing boundary condition for the elastic wave equation[J].Geophysics, 1988,53(8):611-624.

[12]Reynolds. Boundary conditions for the numerical solution of wave propagation problems[J]. Geophysics,1978,43(4):1099.

[13]R F Ungless. An infinite finite element[D]. Canada: University of British Columbia, 1973.

[14]P Bettess, More on infinite elements[J]. Int.J.Numer,Meth.Eng.1980,15(11):1 613-1 626.

[15]G Beer, J L M eek. Infinite domain element[J] Int.J.Numer,Meth.Eng.1981(17):43-52.

[16]O.C.Zienkiewicz et al. A novel boundary infinite element[J].Int.J.Numer,Meth.Eng.1983(19):393-404.

[17]贾坤,蒋树屏,李建军.无限单元在隧道工程数值分析中的应用[J].西部探矿工程,2007(7):135-138.

[18]朱以文，蔡元奇，徐晗.ABAQUS与岩土工程分析[M].香港：中国图书出版社，2005:136-137.

[19]费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2013:54.

[20]夏媛媛,赵民,藏歌,等.正演模拟在解释反演中的应用[J].工程地球物理学报,2014,11(6):842-846.

[21]丘斌煌,晏红艳,李三福,等.底辟模糊区地震资料处理关键技术[J].工程地球物理学报,2014,11(6):824-831.

[22]王敏.地震资料处理中的迭代法衰减多次波技术[J].工程地球物理学报,2015,12(6):800-807.

[23]杨凯,刘伟.基于希尔伯特—黄变换的地震资料高分辨率处理[J].工程地球物理学报,2015,12(1):22-26.

The Application of Infinite Element Boundaries to the Numerical Simulation of Finite Element Earthquake

Li Zhi1，Xue Tingxiao1,2，Zhang Hailiang3

(1.FacultyofEarthSciences,GuilinUniversityofTechnology,GuilinGuangxi541004,China; 2.KeyLaboratoryofGeologicalEngineeringCenterofGuangxiProvince,GuilinUniversityofTechnology,GuilinGuangxi541004,China； 3.ShandongGeologicalProspectingInstitute,ChinaChemicalGeologyandMineBureau,JinanShandong250013,China)

When the finite element method is used to research the numerical simulation of the earthquake, certain boundary conditions are need to apllied to the boundary of the model as for the problems in researching infinite zone. Other methods are more difficult to set up boundary conditions, but using the infinite element method can be more effective to design the absorbing boundary and programming is also more convenient. In this paper, some simple models are designed, the finite element method is used to simulate the model, and the infinite element is designed in the boundary of the model.Then the earthquake snapshot and the artificial earthquake record are obtained.The results of the analysis clearly show that the influence of the boundary of the model is almost eliminated after using the infinite element method, and it can also be used in complex terrain. In solving the problem of infinite domain, infinite element can truly simulate seismic wave propagation process.

seismic numerical modeling; finite element; infinite element

1672—7940(2016)01—0035—06

10.3969/j.issn.1672-7940.2016.01.006

桂林理工大学科研启动项目(编号：002401003302)

李 志(1989-)，男，硕士研究生，主要从事地震数值模拟研究。E-mail：lentureli@163.com

薛霆虓(1974-)，男，副教授，主要从事地震勘探、地球动力学科研和教学工作。E-mail：xuetx@glite.edu.cn

P631.4

A

2015-07-06