例谈“设而不求”在解析几何中的运用
2016-11-25筅江苏省连云港市厉庄高级中学陈卫光
筅江苏省连云港市厉庄高级中学 陈卫光
例谈“设而不求”在解析几何中的运用
筅江苏省连云港市厉庄高级中学陈卫光
“设而不求”,顾名思义就是根据题意巧妙设立未知数并不真正解出来,而是建立“未知”和“已知”之间的关系,从而帮助我们解题,而未知数本身并不需要求出它的值.“设而不求”的方法把关注通过运算求解上升为关注分析求解,即通过少量的计算大量的分析实现解题.“设而不求”的方法在解析几何的一些问题中有诸多应用,它优化了学生的解题思路,让难题的解决更有信心.笔者在平时的教学实践中,发现“设而不求”的方法在解析几何中存在大量的运用,现整理如下,以期抛砖引玉.
一、运用一——点差法
点差法常常用来解决圆锥曲线的中点弦问题,即联立直线和圆锥曲线的方程,借助于一元二次方程的根的判别式、根与系数的关系、中点坐标公式及参数法求解.若设出直线与圆锥曲线的交点(弦的端点)坐标,将这两点代入圆锥曲线的方程并对所得两式作差,得到一个与弦的中点和斜率有关的式子,可以大大减少运算量.我们称这种代点作差的方法为“点差法”.
“点差法”主要适用于题中涉及中点和斜率的问题.如:求中点弦方程、(过定点,平行弦)弦中点轨迹、垂直平分线等问题.
1.证明定值问题
在解答平面解析几何中的定值问题时,如果能适时运用点差法,可以达到“设而不求”的目的,同时,还可以降低解题的运算量,优化解题过程.
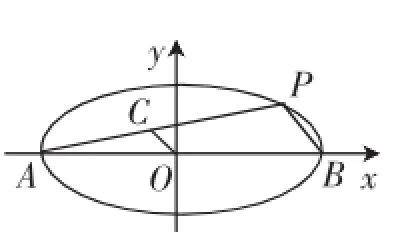
图1
证明:设点A(x1,y1),B(x2,y2),P(x0,y0)(x0≠x1,x0≠ x2),于是,整理得,所以,即又OC//BP,所以kOC=kBP,于是kAP·kBP=-
评注:点差法的特点是题目中有明显或隐含的中点,而中点与斜率又有某种程度的关联.点差法的一般处理程序是设出关键点坐标,然后代入曲线方程,再作差,最后将表达式化成含有斜率与中点的式子.
2.点差法求直线的方程
在解析几何题中,经常已知点在曲线上,求另外相关点的轨迹方程,可以设出相关点,作差求出方程.
例2已知△ABC的三个顶点都在抛物线y2=32x上,其中A(2,8),且△ABC的重心G是抛物线的焦点,求直线BC的方程.
解析:由已知抛物线方程得G(8,0).设BC的中点为M(x0,y0),则A、G、M三点共线,且|AG|=2|GM|,所以G分所成比为2,于是解得,所以M(11, -4).设B(x1,y1),C(x2,y2),则y1y2=-8.又两式相减得y-4.故BC所在直线方程为y+4=-4(x-11),即4x+y-40=0. 3.点差法求点的轨迹
所求点的轨迹是由与之相关的点引起,而相关的点在已知曲线上,因而可以设出相关点,作差求得.例3已知椭圆+y2=1,求斜率为2的平行弦中点的轨迹方程.
解析:设弦的两个端点分别为P(x1,y1),Q(x2,y2),PQ的中点为M(x,y),则两式相减得=0,所以=0.又x1+x2=,所以x+4y=0.因为弦中点轨迹在已知椭圆内,故所求弦中点的轨迹方程为x+4y=0(在已知椭圆内).
4.利用点差法求参数的取值范围
在一类曲线上是否存在关于某直线对称的问题中,经常会求参数的取值范围,此类题中常用点差法解决.
例4若抛物线C:y2=x上存在不同的两点关于直线l:y=m(x-3)对称,求实数m的取值范围.
解析:当m=0时,显然满足.
当m≠0时,设抛物线C上关于直线l:y=m(x-3)对称的两点分别为P(x1,y1)、Q(x2,y2),且PQ的中点为M(x0, y0),则,两式相减得,故.又因为中点M(x0,y0)在直线l:y=m(x-3)上,所以y0=m(x0-3),于是x0=.因为中点M在抛物线y2=x区域内,所以解得-
二、运用二——同构式的运用
同构式,也称为同解式,指在解决圆锥曲线中的直线方程时,式子的结构相同,此时可以设出直线方程,关注式子的形式,从形式的统一性求直线方程,实现“设而不求”目的,大大减少计算量,优化解题过程,是解决此类问题的最佳方法.
例5设P为直线l上的点,过点P作抛物线C的两条切线PA、PB,其中A、B为切点.
(Ⅰ)求抛物线C的方程;
(Ⅱ)当点P(x0,y0)为直线l上的定点时,求直线AB的方程.
解析:(Ⅰ)x2=4y.
(Ⅱ)抛物线C的方程为x2=4y,即y=x2,求导得y′=x.设A(x1,y1),B(x2,y2),则切线PA、PB的斜率分别为,所以切线PA的方程为y-y1=(x-x1),即y=+y1,即x1x-2y-2y1=0;同理可得切线PB的方程为x2x-2y-2y2=0.因为切线PA、PB均过点P(x0,y0),所以x1x0-2y0-2y1=0,x2x0-2y0-2y2=0,所以(x1,y1)、(x2,y2)为方程x0x-2y0-2y=0的两组解.
所以直线AB的方程为x0x-2y-2y0=0.
评注:同构式运用的重点是观察式子结构的特点,从已知的具有相同结构的等式中抽象出直线方程.显然观察法对学生的观察能力,直觉思维有更大的要求的,但是却让学生更加专注于问题分析,而不是大量计算.
三、运用三——运用参数方程
运用参数方程是解决圆锥曲线中与直线有关的动点轨迹的重要方法,该动点往往与动直线有紧密的联系.该方法与点差法有点类似,也需要设出直线与圆锥曲线的交点坐标,不过此时交点坐标被看成参数,然后将所得的式子选择性相乘,通过消参得到动点的轨迹方程.
解析:A1、A2为双曲线的左右顶点,它们的坐标为
A1(-,0),A2(,0),则A1P:y=x+,A2Q:y=,两式相乘得(x2-2).因为点P(x1,y)1在双曲线上,则-=1,即x=,故y2=-(x2-2),即+y2=1.
经检验,以上所得椭圆的四个顶点无法取到,故交点轨迹E的方程为+y2=1(x≠0,且x≠±).
可见,在解决圆锥曲线的一些动点轨迹方程时,运用参数方程也是一种设而不求的方法,它把关注点同样放在了式子的变形上,最终实现简化运算.总之,设而不求在高中数学中有很广泛的运用,笔者仅举几例说明,希望对一线的老师有所启迪.F
