水位变化对半填半挖陡坡路基渗流、稳定性及沉降的影响分析

2016-11-24龙兵

城市道桥与防洪 2016年3期

关键词：陡坡安全系数孔隙

龙兵

（珠海市规划设计研究院，广东珠海 519000）

水位变化对半填半挖陡坡路基渗流、稳定性及沉降的影响分析

龙兵

（珠海市规划设计研究院，广东珠海 519000）

以某城市公园内道路为实例，对半填半挖陡坡路基的渗流、稳定性及沉降进行了分析，探讨了地下水位变化对此类路基内部地下水渗流、边坡稳定性及路基沉降变形量的影响，可为此类路基的设计提供参考。

水位变化；地下水渗流；路基稳定性；沉降变形

0　引言

半填半挖陡坡路基在山区道路设计中较为常见，由于现状地面较陡，陡坡面上的填土如果处置不好，很容易引起滑坡、不均匀沉降等路基病害。水是影响路基稳定性最重要的因素之一，如果半填半挖陡坡路基处于河边或水库边，在汛期常有水位快速升降的现象出现，变化的水位对路基填土会产生动水压力及浮力，地下水会使土体的抗剪能力减弱，边坡稳定的安全系数降低。地下水位变化使路基内部孔隙变化，土体膨胀或收缩，从而影响沉降。

本文采用岩土有限元软件 GeoStudio的SLOPE/W模块、SEEP/W模块以及SIGMA/W模块，以某公园内水库边道路为实例，定量分析水库边半填半挖陡坡路基在水位升降过程中，路基内部渗流、边坡稳定性及沉降量的变化情况，为工程设计提供参考。

1　工程概况

南方某城市公园内道路，局部路段一侧靠山，山体自然坡面较陡，另一侧临近现状小型水库，该段路基是临近水库的半填半挖陡坡路基。选取该段最不利断面进行研究，该处断面现状地面为倾斜陡坡，坡度为1∶1.8，路基宽度为16.3 m（其中含碎落台3 m、边沟0.8 m、机动车道7 m、绿化带2 m、自行车道2.5 m、土路肩1 m），填方高度为14 m，按两级8 m+6 m设置，采用相同坡度1∶1.5。图1、表1为该断面的参数、土层情况。由于自然地面斜坡陡于1∶5，路基横向采用挖台阶处理，每级宽度为2 m。因实际施工时，台阶开挖形状不规则，难以将填挖结合的地方碾压紧密，现状斜坡上的表层土一般强度不高，若渗入雨水，结合部的土强度将会更低。因此，本次分析按不利状态，考虑填挖结合部有软弱滑动带土体约40 cm厚度，见图1。另外，水库底部存在有约2 m厚度的淤泥层，本次采用抛填片石处理。靠水库的边坡坡面采用浆砌片石护坡，厚30 cm，坡脚设置浆砌片石护脚，80 cm顶宽，160 cm底宽，80 cm高度。

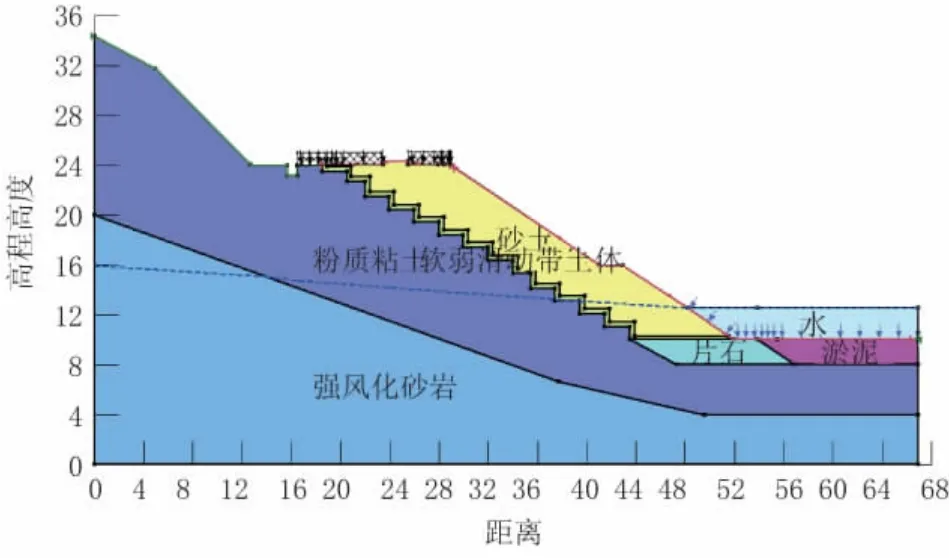
图1　最不利计算断面（单位：m）

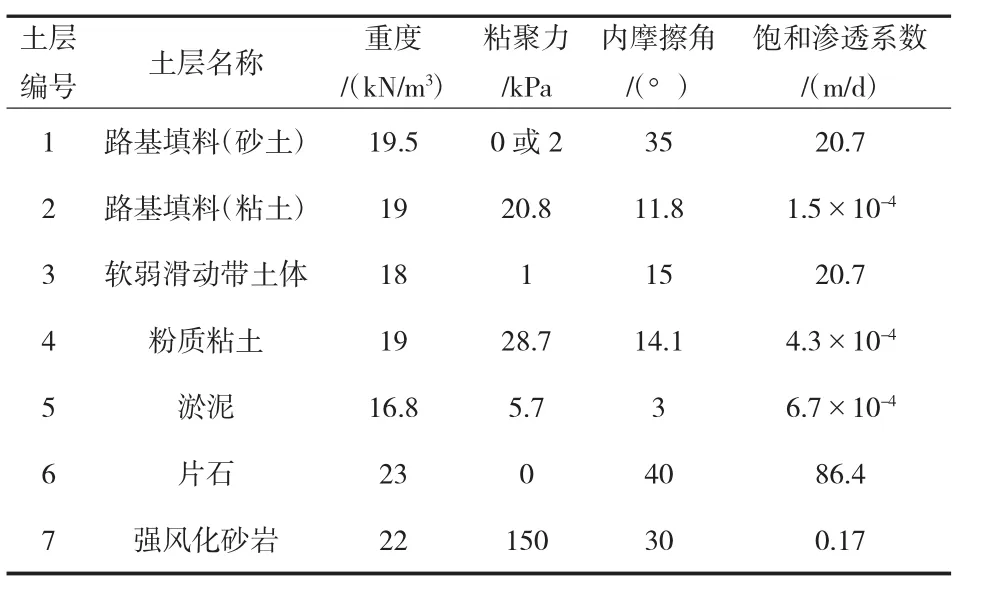
表1　相关计算参数表

2　陡坡路基在常水位时的加格栅处理及稳定性

2.1陡坡路基不加格栅时的边坡稳定性

首先验算路基在无土工格栅时的稳定性，确定该路基是否需要加格栅，以及加格栅的范围。采用SLOPE/W模块为计算工具进行计算，计算方法为摩根斯坦-普瑞斯法。摩根斯坦-普瑞斯法是岩土界公认的较严密的边坡稳定性计算方法，对滑裂面形状无要求，同时满足力、力矩平衡方程。

首先分析路基填土采用砂土的情况。砂土处于干燥、饱和状态时，几乎没有粘聚力，但是处于非饱和状态时，却能表现出较小的粘聚力[1]。本次计算，砂土粘聚力以地下水位为界，水位以下粘聚力取零，水位以上粘聚力取2 kPa[2]。经软件计算，如果路基采用砂性土填筑，半填半挖陡坡路基在无格栅时的安全系数为1.160。

然后将其中的砂土替换为粘性土，计算无格栅时的安全系数为1.170。

根据规范要求，稳定安全系数应不小于1.25，因此，砂土和粘土填筑该陡坡路基，都需要采取加固措施，才能满足设计要求，见图2、图3。

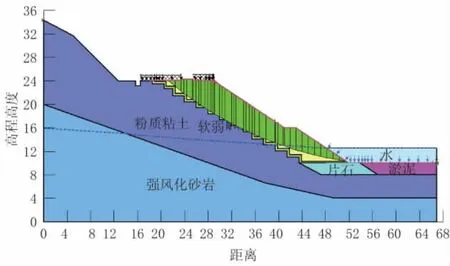
图2　最危险滑动面位置图（填砂土）

图3　最危险滑动面位置图（填粘土）

虽然粘性土粘聚力较大，对路基的稳定性有一定的贡献，安全系数略大，但是，粘性土的渗透系数小，难以疏干渗入路基的雨水，水库边水位升降时，动水压力大，对路基的稳定性不利。综合考虑，建议采用透水性较好的砂土填筑。下文中的计算，路基填土均采用砂土的参数。

2.2陡坡路基加格栅后的边坡稳定性

由于路基填土采用砂性土，砂性土在干燥和饱和时粘聚力为零，容易出现浅层滑动，因此，本次分析考虑边坡全高整体加筋。根据《公路土工合成材料应用技术规范》，对加筋路堤，土工格栅竖向层间距不宜大于80 cm，本次分析首先在路基全高范围按竖向80 cm等间距布置土工格栅，进行初步试算，计算得安全系数为1.22，略小于规范值1.25。从计算结果分析可知，上部的土工格栅对边坡稳定起控制作用，为继续增大安全系数，可将上部约1/3高度的土工格栅加密，改成间距50 cm，计算得边坡的安全系数为1.258，满足规范不小于1.25的要求。图4为路基全高范围格栅间距为80 cm的最危险滑动面位置及形状，图5为上部1/3高度的土工格栅加密间距为50 cm，中下部格栅间距为80 cm的计算结果。

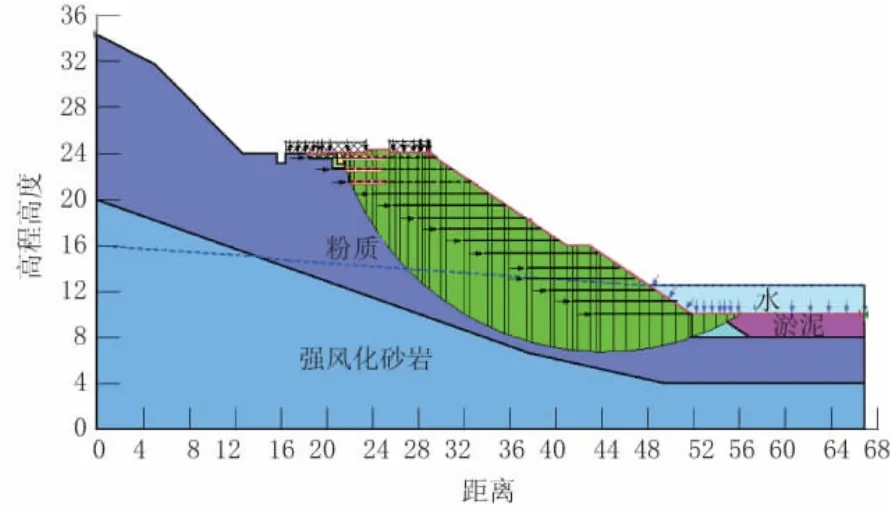
图4　最危险滑动面位置（格栅间距80 cm）

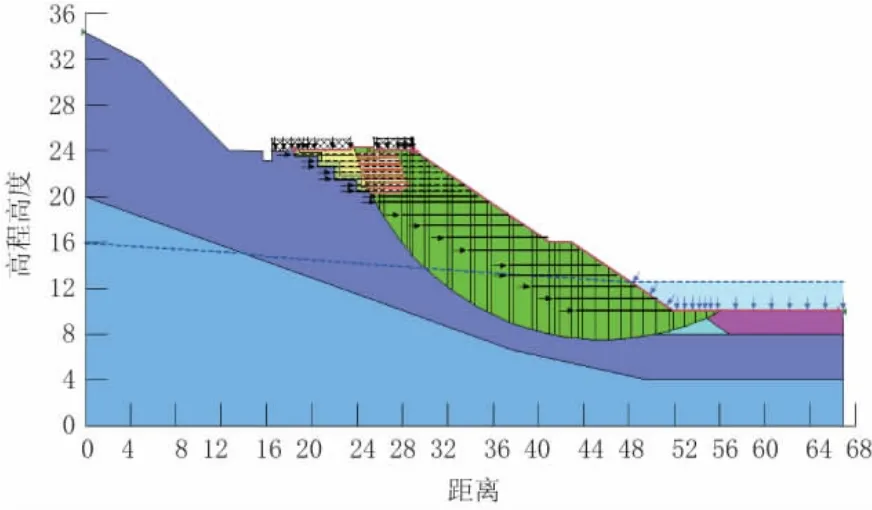
图5　最危险滑动面位置（上部格栅间距50cm）

3　陡坡路基稳定性受水位变化的影响分析

由于道路处于水库边，暴雨时期，水库水位有大幅度上升的情况，暴雨过后以及开启泄洪闸泄洪后，水库水位又会迅速降低。快速变化的水位在路基内部产生渗流，影响路基内部水分的变化，对路基土的粘聚力和内摩擦角产生影响，因此，对边坡的稳定性有一定的影响。本次采用岩土有限元软件GeoStudio的SLOPE/W、SEEP/W模块进行耦合分析，判断路基稳定性受水位变化的影响究竟有多大。

具体分析步骤如下：

（1）采用SEEP/W模块，分析常水位时路基内的孔隙水压力分布情况（工况1），常水位为12.5 m；

（2）采用SLOPE/W模块，分析常水位时的边坡稳定性（工况1）；

（3）采用SEEP/W模块，分析水位上升过程中的渗流情况及孔隙水压力分布情况（工况2），该工况为暴雨期间，2 d内水位由12.5 m快速上升至20.5 m，增幅为8 m；

（4）采用SLOPE/W模块，分析水位180 d持续保持20.5 m不变的边坡稳定性（工况2）；

（5）采用SEEP/W模块，计算泄洪时，水位下降过程中的渗流分析及孔隙水压力分布情况（工况3），最高水位为20.5 m，3 h内快速下降8 m；

（6）采用SLOPE/W模块，计算3 h快速下降8 m过程中的边坡稳定性（工况3）;

（7）采用SEEP/W模块，计算水库水位从常水位开始，快速放干过程中的渗流分析及孔隙水压力分布情况（工况4），1 h内水位由常水位12.5 m至放干，快速下降2.5 m；

（8）计算水库放干过程中的路基边坡稳定性（工况4）。

3.1路基内孔隙水压力、边坡稳定性在常水位时的计算结果（工况1）

工况1计算的是边坡在常水位12.5 m时的孔隙水压力分布情况，孔隙水主要向下部和左侧路基内渗流。工况1的边坡稳定安全系数为1.291，见图6、图7。

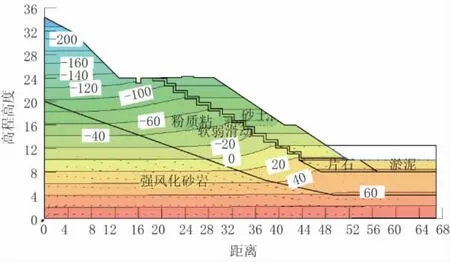
图6　常水位时孔隙水压力（单位：kPa）

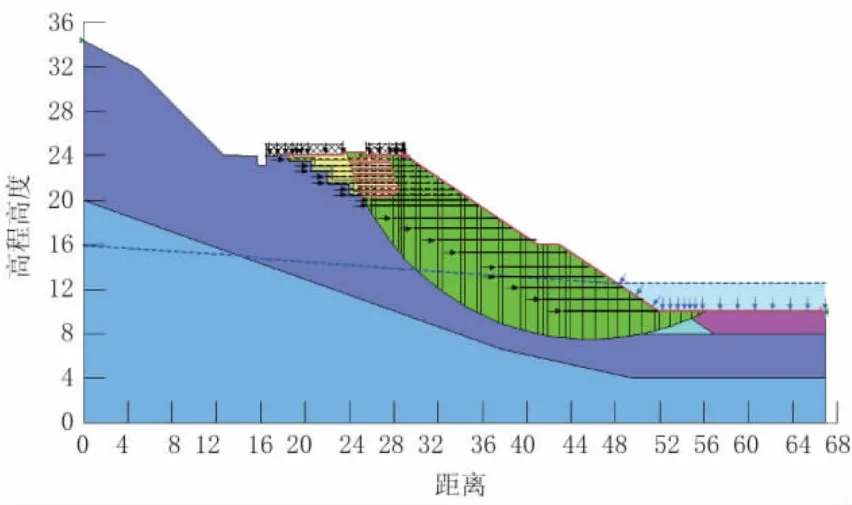
图7　最危险滑动面位置及形状（常水位）

3.2路基内孔隙水压力、边坡稳定性在水位快速上升8 m过程中的计算结果（工况2）

工况2计算的是水库水位在暴雨期间2 d内快速上升8 m的情况。图8反映了工况2的浸润线变化情况。路基内部的浸润线随着水库水位的升高也相应上升。因路基外侧填土为砂性土，渗透系数较大，路基内侧为原状粉质粘土、强风化砂岩，它们的渗透系数较小，所以浸润线在砂性土中上升速度快，在粉质粘土、强风化砂岩中上升速度慢。浸润线对路基内部的粉质粘土及强风化砂岩影响较小。水位在2 d内上升8 m，水位达到20.5 m，浸润线影响范围仅达到距边坡坡脚约13 m的范围。

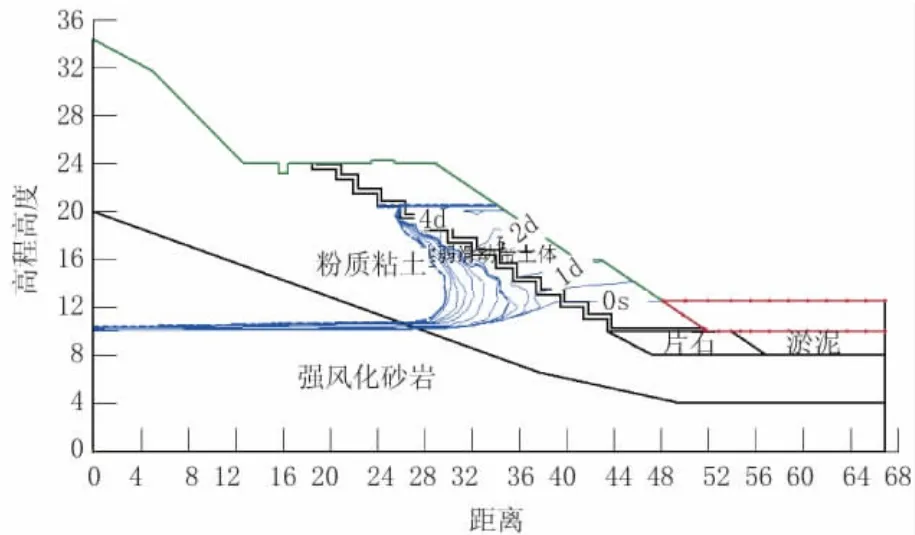
图8　浸润线随水位上升变化图

水位开始上升时，虽然路基土的内摩擦力、基质吸力均有减小，但是因水位升高，水对路基产生的侧向压力增加，且侧向压力起主导作用，使路基的稳定性安全系数增大。水位上升并在一定时间内保持高水位20.5 m不变，在这期间，浸润线在路基内部仍然会持续升高，使得路基土摩擦力、基质吸力会持续降低，而水位不变，水的侧压力不变，所以安全系数会慢慢减小，并在5个月后基本趋于稳定值。图9的安全系数曲线显示了这一变化情况，水位上升8 m，边坡安全系数由1.3增大至1.72，增幅约32%；然后保持高水位一段时间，边坡安全系数有减小的趋势，150 d后慢慢趋于稳定，180 d后安全系数降低至1.58，降幅约8.1%。

图9　水位上升、保持高水位期间的安全系数

3.3路基内孔隙水压力、边坡稳定性在水位快速下降8 m过程中的计算结果（工况3）

工况3计算的是水位达到工况2的最高水位后，在3 h内泄洪，由最高水位20.5 m降低至常水位12.5 m，快速下降8 m。在水位快速下降过程中，路基内部产生了非稳定渗流，地下水位线在路基内部不断变化。图10表示水位由最高水位20.5 m降低至常水位12.5 m过程中浸润线的变化情况。由图10可以看出，随着水位下降，浸润线也在不断下降，开始下降较快，然后慢慢稳定下来。浸润线在砂性土中的变化幅度大，在粉质粘土、强风化砂岩等土层中变化幅度很小，这取决于渗透系数的影响，渗透系数大，路基内部水分运动快，浸润线位置变化快，幅度大。当水位稳定以后，浸润线位置也相应稳定下来。

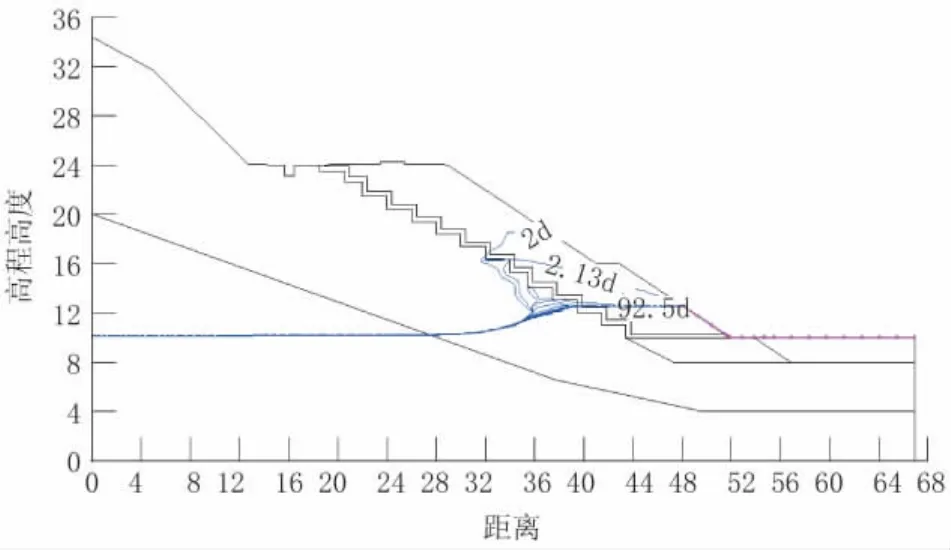
图10　水位下降过程的浸润线位置图

图11反映了路基稳定安全系数随着水位快速下降8 m过程中的变化情况。路基稳定安全系数随水位快速下降，也随之减小。水位在下降8 m的过程中，稳定安全系数从1.72降低到1.281，降低幅度为25.5%；然后保持常水位一段时间，2 d内边坡安全系数略有回升，回升至1.29，然后慢慢稳定，180 d后的安全系数为1.291。

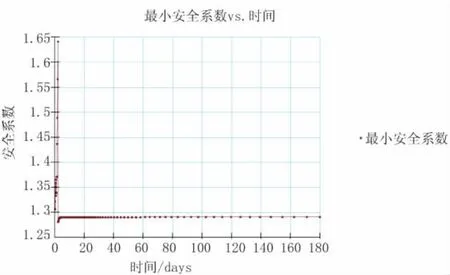
图11　水位下降及保持常水位期间的安全系数

水位降低，路基水分渗透流出路基，浸润线下降，路基土的基质吸力渐渐增大，内摩擦力也逐步增强，对路基稳定性略微有利。但是，水位降低，水对边坡的侧向有利推力也快速减小，并且侧向推力的影响起主导作用，因此，边坡稳定安全系数开始仍表现为减小。随着时间延长，水位维持在常水位一段时间，水的侧向推力基本保持不变，土的基质吸力、内摩擦力则继续增长，使得稳定安全系数在下降后又略有上升，再趋于稳定，图11显示了这一变化趋势。

3.4路基内孔隙水压力、边坡稳定性在常水位至快速放干过程中的计算结果（工况4）

工况4计算的是水位在2小时内放干，由常水位12.5 m降低至水库底10.0 m，快速下降2.5 m。在水位快速下降过程中，路基内部产生了非稳定渗流，地下水位线及浸润线在路基内部不断变化。图12中，浸润线位置随着水位由常水位至放干过程而逐渐下降并慢慢稳定下来。与工况3类似。

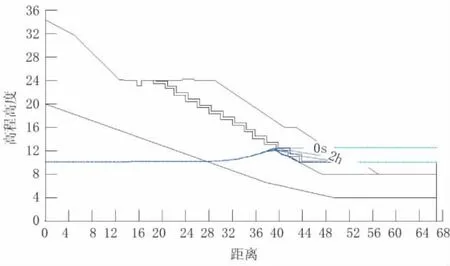
图12　水位放干过程中的浸润线位置图

图13反映的是水位由常水位至放干过程中，路基边坡稳定安全系数变化情况。水位由常水位至放干过程中，路基稳定安全系数随之迅速降低，然后又略有上升。水位下降2.5 m，稳定安全系数从1.253降低到1.236，降低幅度为1.4%；然后保持放干状态一段时间，15 h内边坡安全系数略有回升，回升至1.249，然后慢慢稳定下来，相比常水位时的安全系数，降幅约0.3%。

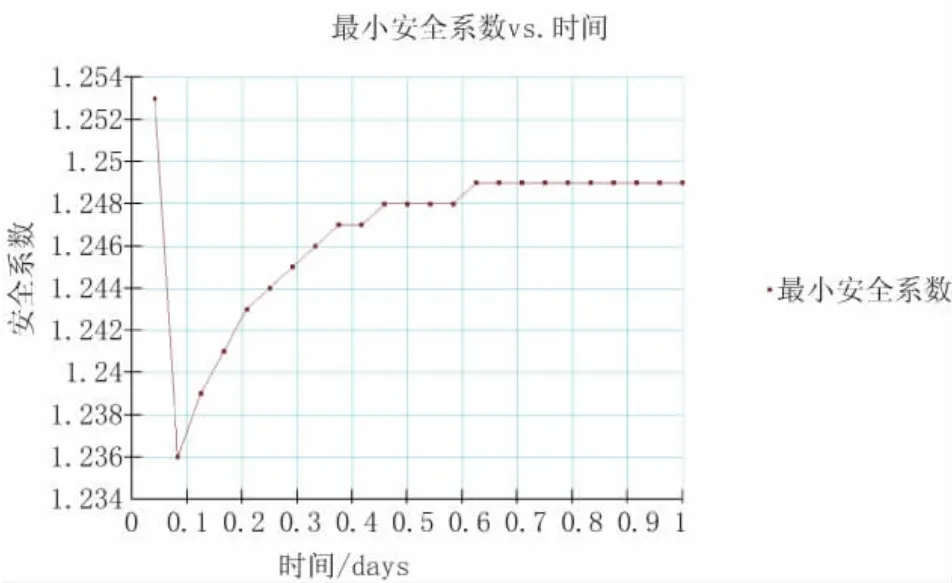
图13　水位放干过程中的安全系数

工况4的浸润线、安全系数变化趋势与工况3的情形类似，变化的原因也与之类似，在此不再赘述。

根据工况4的计算结果，水位由常水位至放干过程中，稳定安全系数仅1.236，为以上4种工况中最不利的情况，小于规范规定值1.25。因此，需进一步加强路基安全措施，将顶部格栅间距调整40 cm，经计算，加密格栅后安全系数能达到1.26，满足设计及规范要求。设计时对这种情况应重点考虑。

4　陡坡路基的沉降变形受水位变化的影响分析

本次利用SEEP/W模块、SIGMA/W模块进行耦合分析，探讨陡坡路基内部孔隙水运动与路基变形之间的关系。

本次仅分析水位上升及下降过程中，路基内孔隙水变化与路基变形之间的相关关系。首先采用SEEP/W模块分析路基在常水位时的孔隙水压力情况，再将常水位时的孔隙水压力导入SIGMA/W模块计算初始应力情况。以此为基础，再进行耦合分析，计算水位变化引起的孔隙水压力变化、应力变形变化。以下计算结果中x方向位移以向右为正，y方向位移以向上为正。

（1）水位由常水位12.5 m在2 d内上升至20.5 m过程中，路基沉降变形情况。

经计算，路基右上角点的位移变化情况如下：常水位时的x方向位移为5.6 mm，y方向为-7.2 mm，水位升高至20.5 m时的x方向位移为11.9 mm，y方向位移-3.6 mm。x方向位移增加了6.3 mm，y方向位移减小了3.6 mm。

（2）水位由最高水位20.5 m在3 h内下降至12.5 m过程中，路基沉降变形情况。

经计算，路基右上角点的位移变化情况如下：最高水位时的x方向位移为11.9 mm，y方向为-3.6 mm，水位下降至12.5 m时的x方向位移为7.8 mm，y方向位移-5.8 m。x方向位移减小了4.1 mm，y方向位移增加了2.2 mm。

从以上计算结果可知：随着水位升高，x方向位移有所增加，y方向位移有所减小。随着水位降低，x方向位移有所减小，y方向位移有所增加。水位上升，水向路基内渗透，路基土体积含水量增加，体积有膨胀趋势，因此，水平位移有增加的趋势，竖向位移有减小的趋势，但是变化幅度不是很大。相反，水位下降，因水从路基内渗出，路基有收缩的趋势，所以水平位移会减小，竖向位移会增加。