统计学建模法在面积性高密度电阻率数据反演中的应用

程 勃，丁彦礼，徐志锋

（桂林理工大学　a.广西隐伏金属矿产勘查重点实验室；b.地球科学学院，广西桂林 541004）

统计学建模法在面积性高密度电阻率数据反演中的应用

程 勃，丁彦礼，徐志锋

（桂林理工大学a.广西隐伏金属矿产勘查重点实验室；b.地球科学学院，广西桂林 541004）

在面积性的勘查工作中，为了能够通过高密度电阻率数据反演获得详细的地层结构和岩性信息，采用了基于统计学方法建立初始模型的反演算法。该方法充分地利用高密度实测数据建立初始模型，对单个剖面实施遗传算法反演，将其反演结果作为初始模型用于相邻剖面数据的反演。实例表明，该方法大幅度降低了初次拟合误差，减少了反演计算量，使反演结果较好地反映出测区范围内的地层结构特征和岩性分布情况。

电阻率法；二维反演；统计学建模；天然气管道

0 引 言

高密度电阻率法广泛应用于工程地质勘查工作中，主要解决分层及探测地质构造等问题。由于高密度电阻率法同时具有电阻率剖面法和测深法的特点，在工程场地勘查中往往进行包含多条平行测线的面积性测量，人们期待高密度电阻率数据反演能够给出尽可能详尽的三维地下结构特征［1-3］。

由于三维反演计算时间长，还不能广泛用于实际工作［4-6］。对于多条测线的面积性高密度电阻率测量，还是以二维反演为主。在常规二维反演解释过程中，每条测线是独立进行解释的，反演图像是电阻率连续变化的等值线图，是地下介质的电性成像，没有明确的地层结构信息，需要数据处理人员根据经验分析解释出地层结构、分层和电阻率信息［7-9］。有时，测线间的距离不大，解释软件给出的不同测线地电断面电性差异却比较大，增大了解释人员综合分析推断的难度［10-12］。

统计学建模反演方法［1-3］以电阻率测深数据的统计学特征建立二维地层结构初始模型，这种模型具有地下的地层结构和电性参数。利用改进的遗传算法修改地层结构和层参数，并在修改模型的反演过程中充分考虑先验信息。这样反演的最终结果具有明确的地层结构和具体的层参数信息，并可以直接与地质构造、岩性等信息对应。在面积性测量时，测区内包含多条距离较小且相邻的剖面，根据常理和经验可以假设，相邻剖面的地层结构和岩性有相似之处。因此，通过处理一个剖面资料获得的反演地层结构和层参数可以推广到相邻剖面上。

本文尝试在面积性勘查的高密度电法数据处理中使用统计学建模方法反演，利用原始数据的统计学信息并结合地质资料，建立最贴近实际的初始模型。用多剖面统计学特征值判断地层结构、获得层参数并建立二维地质模型。对某一剖面进行二维反演，完成单个剖面的反演后，使用反演结果作为相邻剖面的反演初始模型，对其他剖面反演。这样既提高了反演速度，又控制了区域内的模型参数差异。这一处理方法与常规方法相比的优点是：反演结果有明确的地层结构和具体的层参数信息，可以直接与地质构造、岩性等信息对应，在测区内地质条件变化不大、相邻测线高密度电阻率异常特征相似的情况下，将某一剖面的反演结果用于相邻测线，既提高了反演速度，又可以使测区的地层结构和层参数具有统一性，利于进一步的地质解释。值得注意的是，当测区内地质条件变化大、电阻率异常特征差异大时，需要解释人员先将测线分区，然后再进行反演解释。

本文用统计学建模方法对某天然气管道基础勘探测区3条测线的高密度电阻率数据进行反演。反演出的测区勘探深度范围内的地层结构特征和岩性分布状态，将高密度电法反演解释结果直接与地层结构联系起来，提高了资料解释的准确性，增强高密度电法勘探的准确性和实用性，得到了较好的地质效果。

1　统计学建模反演方法和步骤

1.1统计学建模流程

统计学方法建模流程如图1所示，主要步骤分为：（1）处理实测数据并判断地层结构类型（图1主干部分）；（2）确定地质体空间位置（图1右侧部分）；（3）加入先验信息（图1左侧部分）；（4）建立初始模型。

1.2统计权重的分配

在图1中，当模型类别被判断为含横向变化（如存在断裂）时，需要确认电性横向变化的位置及两侧的地层结构和层参数。为此，统计电阻率测深数据各极距视电阻率的水平方向梯度。水平梯度的极值位置信息可以辅助完成初始模型结构类别判断，并获得断裂或岩性接触面的初始位置［1-2］。数值模拟结果和实测资料证明，浅部的局部异常体同样会造成水平梯度出现极值，可能造成对主要异常体位置判断失误。因此在水平梯度统计过程中根据探测目的设置统计权重，例如，在探测断裂、岩性接触带或深部异常体时，对深部信息赋予较大的统计权重。

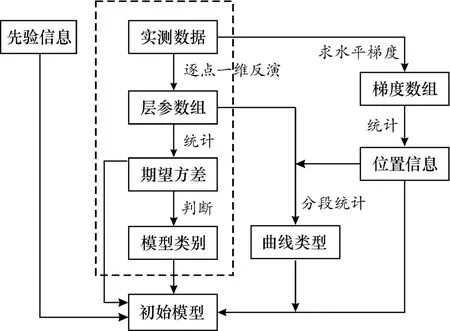
图1　统计学建模流程Fig.1 Process of statistic modeling

以低阻断裂为例，断裂左边界确定函数为

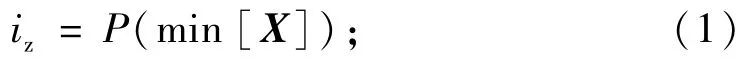
断裂右边界确定函数为

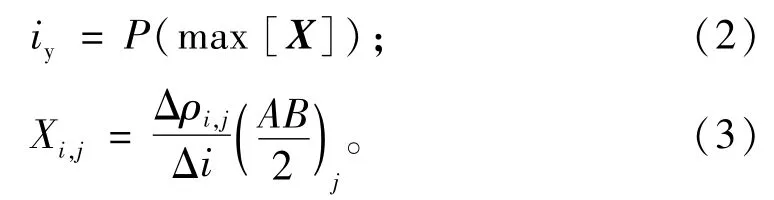
其中：Δρi，j/Δi为视电阻率在水平方向上的变化率，亦为权重因子；i为测点号；j为极距号。P（x）的作用是求x在测线上的位置。

如果是岩性接触带类模型，则视接触面两侧的电阻率大小关系采用式（1）和式（2）中的一个。

1.3测区内电阻率参数的确定

对地层中含有横向电性变化的情况下，初次统计的层参数数学期望只能作为判断的信息，不能作为初始模型层参数初值。利用式（1）、（2）获得各剖面的横向电性变化位置后，分别统计横向电性变化位置（断裂或接触面）两侧测点的一维反演层参数、测深曲线类型、同类型曲线的数量及所占总曲线数量的份额。由此，以占较大份额的曲线类型作为某一侧的初始地层电性结构。

1.4先验信息的加入

测区的先验性信息，包括地质构造、地层岩性及地球物理信息，是地球物理勘探资料解释中必须参考的信息。结合先验信息判断地层结构，能降低局部和浅部异常体对整体地层结构判断的干扰。

在以寻找断裂为目标的面积性勘查工作中，测线布置往往垂直断裂走向，因此测区内间隔不太远且平行的测线很可能位于同种类型的地层结构之上，而且很多模型参数都是相互近似的。测区内的钻孔资料提供了地层结构和岩性信息，加入这些信息，使初始模型更接近实际的地电结构。在反演过程中，由先验信息设置的参数不参与遗传变异，子模型数量减少，对提高反演速度也有一定的作用。

1.5修正的遗传算法修改层参数

建立初始模型之后，采用有限元方法计算模型的视电阻率，根据模型计算值和实测值的差异，采用修正的遗传算法修改模型，反演出地层结构参数和层参数［1-3］。

遗传算法是非线性反演中的常用方法，遗传算法遗传、变异样本并正演计算，需要的计算时间与模型数量呈正比。利用统计学建模方法已经设定的初始模型，在繁殖子模型的过程中，限制了参数的变异方式：地层或地质体电阻率的变异，每次变异的幅度为当前值的10%；空间位置类参数，包括断裂的左右边界、接触面的位置、地层的厚度等这些参数每次改变量为一个单元网格（有限单元法正演中的剖分网格）。

在修改参数的过程中，首先调整电阻率参数，在初始模型的基础上于10%的范围内搜索更接近于实际模型的层参数，然后固定电阻率参数，根据局部误差修改各点的层厚度。这样可以节省计算时间，又不至于大幅度修改初始模型。

这样的修改参数方式相当于搜索法，从初始模型开始，繁殖出参数变异的子模型，每个子模型每次仅有1个参数发生变异。因为每个参数有两种变异方式（增加/减少，提高/降低，左移/右移），所以每次繁殖的子模型数量是参数个数的2倍。对这些模型进行有限元数值模拟并计算拟合误差。误差最小的子模型存活并成为新的繁殖起点，开始新一轮的繁殖和筛选。这样循环若干次，直至拟合误差无法降低时反演结束，最终存活的模型为反演结果。这种修正的遗传算法，在修改初始模型参数的同时，不修改初始模型的地层类型，减少了计算量。

当需要解释的资料包含多个相邻剖面时，先采用单剖面反演，反演结果作为相邻剖面的反演初始模型，这样做的好处是合理的降低了反演计算量，保持相邻剖面结构统一以及主要参数接近，便于在多剖面反演结束时对测区的三维结构进行推断。

2　应用实例

广西天然气输气管道工程跨越数百千米，沿途地质条件复杂，断裂或岩性接触带附近是需要重点勘探的区域。天然气管道穿越柳州市雒容镇附近的洛清江。洛清江西岸测线范围内，大部分为第四系冲洪积（）粘土、粉质粘土，测线小号点约40～50 m附近有小范围砂岩出露。测线大号点约180 m处，钻探取心的情况为：第四系冲洪积）粘土、粉质粘土层；含砾粘土、卵石层；下部为石炭系中统（C2）白云岩、灰岩，风化严重。要求利用高密度电法勘探查明断裂（砂岩和白云岩的接触位置）及断裂两侧地层分布等情况。

2.1测线布置及高密度电阻率数据的采集方法

沿设计管道轴线在地表的投影以及左右两侧各10 m布置了3条高密度电法测线（a1、a2、a3），3条测线长度均为840 m。测量仪器为WDJD-2型多功能数字高密度电阻率仪。根据勘查要求，采用联合三极装置，即在一条测线上同时进行AMN和MN-B测量。采用的测量电极距为10 m，点距10 m，测量层数为8层，对应供电极距AO为15～85 m。

2.2实测数据的初步统计分析判断地层结构

根据地质及钻孔资料可知，断裂位于测线40～180 m范围内，因此断裂定位解释主要在该范围内进行。使用实测的2组三极装置数据组合出对称四极测深数据，3条0～300 m剖面范围内的视电阻率断面等值线如图2所示。可以看出，3条剖面的视电阻率变化规律基本相似，在150 m附近有明显的电性差异，小号点一侧视电阻率较低，在50～150 Ωm范围内，大号点一侧在150 Ωm以后，呈现出起伏层状特征。

3条剖面的视电阻率特征基本一致，但使用常规的反演软件解释出的电性参数差异较大，无法根据解释结果统一给出断裂位置和各层深度等信息。因此，采用统计学建模方法进行反演，处理的步骤如下：

按照图1统计学建模流程图的步骤，首先根据钻孔资料和视电阻率分布情况，将探测深度范围内的地层确定为3层，对a1、a2、a3剖面上各测深点的数据进行一维反演，获得各点的电阻率和地层厚度参数，对这些层参数分剖面统计数学期望和方差。其中，a1剖面统计结果如表1所示。

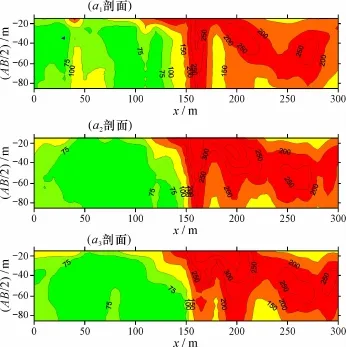
图2　实测视电阻率断面等值线图Fig.2 　Contour map of measured apparent resistivity section

表　1 a1剖面一维反演参数统计结果Table 1 Layer parameters statistic result of Profile a1

对照文献［1］中的判断规则，3个剖面的统计数据都支持判断地层结构为直立异常体（断裂）。文献［1］中的地层结构判断方法是根据各种地层结构模型的正演数据统计归纳后得出的统计规律。

作出测区地层结构为直立异常体（断裂）初始判断后，参考地质资料修正地层结构。从测区地质资料可知：测线小号点一侧有砂岩出露，大号点一侧基岩为灰岩，判断测区内地质结构为有覆盖层的接触面结构，接触面两侧的岩层电性不同。

2.3各剖面断裂（岩性接触面）位置的确定方法

为了确定各剖面断裂（岩性接触面）位置，按照图1统计学建模流程图的步骤对实测视电阻率数据求各极距的水平梯度，用1.2节中求断裂边界的式（2）确定接触面位置，这一方法的实质是利用不同极距的视电阻率的水平梯度变化确定电性变化的边界。为确定深部的电性变化位置，以大极距水平梯度信息为主要依据。a1剖面的水平梯度曲线如图3a所示，包括极距为75和85 m的水平梯度曲线，水平梯度的极大值点在剖面的150 m处。图3b是极距为75和85 m的视电阻率曲线，可以看出，以剖面中间为界，两侧有明显的电性差异。其他两条剖面（a2、a3）水平梯度和视电阻率曲线与a1剖面类似。由此，初步确定岩性接触面在a1剖面的150 m处。

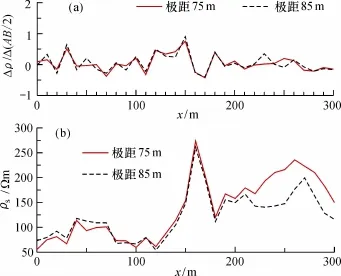
图3　a1剖面的水平梯度和视电阻率曲线Fig.3 Horizontal grade and apparent resistivit curves of Profile a1

2.4初始模型层参数的确定

按照统计学建模流程图（图1）的步骤，确定了岩性接触面的位置后，对a1剖面150 m（断裂位置）两侧重新分别统计电阻率测深曲线类型及层参数的数学期望，各统计参数如表2所示，左侧表示小于150 m一侧，右侧表示大于150 m一侧。从表2可知，岩性接触面的左侧，电阻率测深曲线的类型主要为H型，右侧的曲线类型主要为K型。

表2　a1剖面接触面两侧曲线类型统计结果Table 2 Curve type and layer parameters’expect for each side of Profile a1

2.5使用统计学参数建模

综合2.2、2.3和2.4节的统计学方法确定的岩性接触面位置、断层边界两侧层参数等信息建立的a1剖面的反演初始模型见图4，初始模型中各区块的电阻率如模型中图例所示。从a1剖面的初始模型可以直观地看到测线范围内的地层结构，电性分布的大致情况。

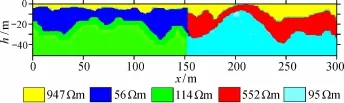
图　4 a1剖面初始模型Fig.4 Initial model of Profile a1

3　修正的遗传算法反演效果

使用图4的初始模型进行反演拟合，初次拟合误差在100%以上。按照1.5节中的修正的遗传算法反演步骤，分别修改岩性接触带边界、电阻率和层厚度参数，最终获得的反演结果断面如图5所示。a1测线的拟合误差为22.4%。与初始模型相比，地层结构没有变化，反演改变了电阻率和界面深度。

由于a2与a1相邻且间距只有10 m，a2剖面的反演用a1的反演结果作为初始模型，这样选择初始模型的好处是大幅度降低了计算量，也省去了图1中统计学建模的各个步骤，初次计算拟合误差仅为25.4%。反演完成时a2剖面的拟合误差为21.9%，从初始模型到反演结束所需计算量大大少于a1剖面。

使用a2剖面的反演结果作为a3剖面的反演初始模型，初次计算拟合误差为26.7%。反演完成时，a3剖面的拟合误差为21.6%。3条剖面的反演结果如图5所示，各剖面均有明确清晰的地层结构和层参数信息，各剖面的电阻率变化较小，从反演结果可以看到下层岩性接触面从a1到a3剖面逐渐向大号点移动。

为了证明统计学建模方法的反演效果，以图5各剖面反演结果为模型，用有限元方法计算了视电阻率断面等值线图，结果如图6所示。与图2实测数据的断面等值线图对比，两者的等值线图像的主要特征基本相似。正演计算与实测数据的平均拟合误差为22.0%。

图5的反演成果给出了各剖面岩性接触带（即通过测区的断层）的位置、断层两侧的地层分层信息，及各层的厚度变化情况。与钻孔资料对比，层厚度基本准确。综合各剖面反演结果可以看出，接触面位置在a1剖面的140 m、a2剖面的145 m、a3剖面的150 m处，从而推断出接触面的走向。

图5　各剖面反演结果Fig.5 　Inversion model for each profile

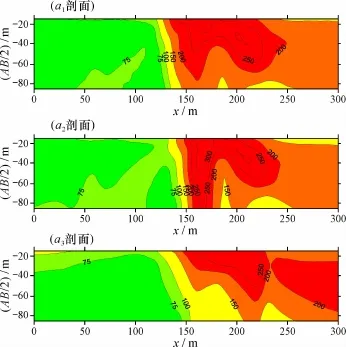
图6　各剖面反演结果的正演计算结果Fig.6 Stimulation result of inversion model for each profile

4　结 论

采用统计学建立初始模型的反演方法可以有效完成对地层结构的判断，并利用水平梯度确定接触带位置。将地质资料作为先验信息参与到反演过程中，减少了遗传算法的计算量。

应用实例表明：应用统计学、水平梯度计算和先验信息融合的方法尽可能利用了高密度电法实测数据和地质信息，建立了最大限度接近真实的初始模型。初始模型建立后，使用遗传算法配合有限元正演模拟调整模型参数，完成了非线性反演。在反演结果中，地层结构被明确显示出来，地层厚度、电阻率和分界面位置都有明确的数值。

在面积性高密度电法勘探资料解释中，当测区内地质条件变化不大、相邻测线高密度电阻率异常特征相似时，有必要利用好相邻测线的反演结果。将某一测线的反演结果用于全测区，既提高了反演速度，又可以使测区的地层结构和层参数具有统一性，利于进一步的地质解释，提高反演的速度和质量。

电法勘探中还有其他测深类方法，例如激发极化测深、频率测深及瞬变电磁测深等和电阻率测深有类似数据结构的方法，也可以用统计学建模方法建立初始模型并进行反演，预期可以获得较好的地质效果。由于影响岩土层电性变化的因素很多，自然界中地下电性结构非常复杂。如何处理复杂的地层结构以及含有各种干扰因素的野外实测数据，统计学建模法还需要进一步探索研究和完善。

［1］程勃，底青云.基于遗传算法和统计学的电阻率测深二维反演研究［J］.地球物理学进展，2012，27（2）：788-795.

［2］程勃，底青云.基于偏导数和统计学方法的电阻率测深二维反演［J］.石油地球物理勘探，2012，47（6）：1006-1013.

［3］程勃，底青云.复杂地电结构条件下统计学建模法电阻率测深二维反演 ［J］.地球物理学报，2014，57（3）：961-967.

［4］阮百尧，村上裕，徐世浙.电阻率/激发极化率数据的二维反演程序［J］.物探化探计算技术，1999，21（2）：116 -125.

［5］苏朱刘，胡文宝，严良俊.电阻率和极化率测深法的正演修正法反演［J］.石油物探，2005，44（2）：194-198.

［6］何门贵，温永辉.高密度电阻率法二维反演在工程勘探中的应用［J］.物探与化探，2002，26（2）：156-159.

［7］底青云，倪大来，王若，等.高密度电阻率成像［J］.地球物理学进展，2003，18（2）：323-326.

［8］赵改善，译.求解非线性最优化问题的遗传算法［J］.地球物理学进展，1992，7（1）：90-97.

［9］刘斌，聂利超，李术才，等.三维电阻率空间结构约束反演成像方法［J］.岩石力学与工程学报，2012，31（11）：2258-2268.

［10］阮百尧.电阻率/激发极化法测深数据的一维最优化反演方法［J］.桂林工学院学报，1999，19（4）：321-325.

［11］阮百尧.电阻率测深解释中的一种新的反演方法 ［J］.桂林冶金地质学院学报，1994，14（1）：80-85.

［12］吕玉增，阮百尧.高密度电法二维反演软件设计与实现［J］.桂林工学院学报，2004，24（4）：417-421.

Statistic modeling 2D inversion application in parallel resistivity survey lines

CHENG Bo，DING Yan-li，XU Zhi-feng
（a.Guangxi Key Laboratory of Hidden Metallic Ore Deposit Exploration；b.College of Earth Sciences，Guilin University of Technology，Guilin 541004，China）

For the key geophysical information，statistic modeling inversion is applied in a survey area with a few parallel survey lines.This method makes full use of the field data to get initial model，and complete the inversion with genetic algorithm.One line's inversion result became the initial model of the next line.The example proves that this method reduces the fitting error effectively.The inversion results of lines show the geophysical characteristic in the survey area.

resistivity；2D inversion；statistic modeling；gas pipe

P631.322

A

1674-9057（2016）03-0452-06

10.3969/j.issn.1674-9057.2016.03.006

2015-04-28

国家自然科学基金项目（41404116）；广西自然科学基金项目 （2014GXNSFBA118232；2014GXNSFAA118305）；广西隐伏金属矿产勘查重点实验室系统研究课题 （15-140-27-06）

程 勃 （1982—），男，博士，讲师，研究方向：地球物理正反演，chengbo@glut.edu.cn。

引文格式：程勃，丁彦礼，徐志锋.统计学建模法在面积性高密度电阻率数据反演中的应用［J］.桂林理工大学学报，2016，36（3）：452-457.