Flight safety measurements of UAVs in congested airspace
2016-11-24XiangJinwuLiuYangLuoZhangping
Xiang Jinwu,Liu Yang,Luo Zhangping
School of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China
Flight safety measurements of UAVs in congested airspace
Xiang Jinwu,Liu Yang,Luo Zhangping*
School of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China
Describing spatial safety status is crucial for high-density air traffic involving multiple unmanned aerial vehicles (UAVs) in a complex environment.A probabilistic approach is proposed to measure safety situation in congested airspace.The occupancy distribution of the airspace is represented with conflict probability between spatial positions and UAV.The concept of a safety envelope related to flight performance and response time is presented first instead of the conventional fixed-size protected zones around aircraft.Consequently,the conflict probability is performance-dependent,and effects of various UAVs on safety can be distinguished.The uncertainty of a UAV future position is explicitly accounted for as Brownian motion.An analytic approximate algorithm for the conflict probability is developed to decrease the computational consumption.The relationship between safety and flight performance are discussed for different response times and prediction intervals.To illustrate the applications of the approach,an experiment of three UAVs in formation flight is performed.In addition,an example of trajectory planning is simulated for one UAV flying over airspace where five UAVs exist.The validation of the approach shows its potential in guaranteeing flight safety in highly dynamic environment.
1.Introduction
With increasing numbers of unmanned aerial vehicles (UAVs) and expanded operations into complex mission scenarios,aviation safety is facing a new challenge caused by highdensity air traffic in limited airspace.Emergency rescue and formation flying usually suffers in congested airspace.The same problem is encountered by civil aviation when reducing flight separation to improve transportation efficiency and increase airspace capacity,and also by certain innovative techniques under development,such as autonomous risk avoidance and free flight.In order to accomplish complicated military missions safely and effectively,coordinated formation flight (CFF) has been investigated by many researchers.The increase of collision risk among UAVs results in flight safety problems more serious than ever.1Fundamentally,an intuitive representation of airspace safety and,especially its tendencies are crucial to solving this issue.This leads to the requirement for timely and credible constructs of safety in congested airspace.
The complexity of air traffic dense flight lies in environmental dynamics;therefore,the airspace situation varies dynamically.There are often many maneuvers in low altitude flight,especially for UAVs,and the highly dynamic motions result in difficulty for risk assessment of flight routes.In civil aviation,reliable risk assessment approaches for fixed routes have been developed by Reich2–4and Brooker.5These methods employed historical statistics to assess the long-term longitudinal,lateral and vertical conflict risks.Assessing airspace complexity in a mid-term horizon has recently attracted more research interest since timely identification of dangerous encounters requiring evasive maneuvers can lead to more efficient air traffic control (ATC) system operations.6Sridhar et al.describe airspace complexity by the predicted dynamic density.7Prandini et al.present an analytic model of air traffic complexity in three dimensional airspace.8Due to the presence of flight errors,approaches to evaluate conflict probability involve predicting future aircraft trajectories and computing the probability that two aircraft get closer than a minimum required separation based on these trajectories.9–13Usual methods focus on midterm conflict prediction via the geometric analysis of aircraft relative position.The Monte Carlo approach is a popular method for conflict resolution in the presence of uncertainty in aircraft dynamics,14–16though it takes a great amount of computation.Nevertheless,these methods are a posteriori and not appropriate for dynamic and congested airspace.In this work,the occupancy distribution of the airspace,which is represented with conflict probability between spatial positions and UAVs,is proposed as the determinant of airspace safety.In this way,one can have explicit awareness about airspace congestion for a predicted time interval.
In maneuvering flight,aircraft need to frequently perform conflict prediction and resolution;at present,flight routes are varied,and separation minima is difficult to maintain.In conflict prediction,aircraft may encounter intruders from any direction,thus the minimal safe separation is replaced by a protected zone around aircraft(the REICH model is actually a cuboid protected zone).Due to the different kinetic characteristics and flight performance between various types of aircraft,the prescribed protected zone for conflict prediction should relate to aircraft performance.Some research methods,such as the computation of reachable sets,have been developed for this issue.The mathematical formulation of protected zones is generally related to the reachability analysis of aircraft dynamic systems.The analysis attempts to divide the airspace into two parts:those that are reachable from the initial conditions and those that are not.Recently,some contributions have dealt with the mathematical description of reachable sets and their numerical computation.17–21Considering that the encounter model is key for assessing conflict probability,we present the safety envelope as the protected zone that should not be penetrated by intruders.It indicates the maximum range that a UAV could reach in a specified response time,the n relates the UAV performance to conflict probability.
The rest of the paper is organized as follows:in Section 2,the definitions of UAV safety envelope and airspace safety are introduced;a probabilistic approach for the measure of airspace safety is presented.In Section 3,we analyze the effect of UAV flight performance on conflict probability and construct the airspace safety field.In Section 4,two applications based on airspace safety are presented.In Section 5,conclusions are drawn.
2.Airspace safety
2.1.UAV safety envelope model
The safety envelope is used to characterize the space range that a UAV can reach in a certain time frame.It is an enclosed space determined by UAV flight performance and prescribed time frame.In Fig.1,the six axes a,b,c,d,e,f represent the maximum range that UAV A is able to reach in each direction during the time frame[0,τ].The safety envelope E(XA)is composed of eight different one-eighth ellipsoids.The axes e and f are equal due to the bilateral symmetry of UAV flight performance.However,axes a,b,c and d are different.The specified response time is denoted as τ,andVf,Vb,Va,Vd,Vlare the maximum forward velocity,the maximum backward velocity,the maximum vertical ascending velocity,the maximum vertical descending velocity and the maximum horizontal lateral velocity of a UAV,respectively.Hence,we have the maximum range in each direction
In the inertia coordinate system O-xyz(see Fig.1),for UAV A whose position is XA=[xA,yA,zA]T,we define the safety envelope E(XA)as the region centered at XA

where Mi∈R3X3(i=1,2,3,4)is a diagonal matrix given by and M is a function of M1,M2,M3and M4


Fig.1 Safety envelope of UAV A.

Thus,we can rewrite E(XA)as

The safety envelope provides maneuvering space for a UAV.In other words,a UAV can perform any maneuver in the safety envelope during the time frame[0,τ]without worrying about conflicts with other aircraft.Obviously,the shape of the safety envelope depends on the five velocities that represent UAV flight performance.The parameter τ controls the size of the safety envelope.
2.2.Flight state propagation
Measuring airspace safety involves the estimation of conflict probability,which is only as reliable as the ability of UAV motion model to predict the future.The key to modeling lies in how current UAV states are projected into the future.In the proposed model,future UAV position depends on two elements:the nominal trajectory and uncertainties.Usually,uncertainties are modeled to describe potential variations in the nominal trajectory of a UAV(see Fig.2).
Suppose UAV A is flying along a nominal trajectory with a velocity profile vAin the three-dimensional airspace S⊂R3during the time horizon[0,t].represents UAV initial position at time t=0 s.The UVA's future position is not known precisely due to uncertainty.However,in practice,the prediction error can be modeled through a Gaussian random perturbation whose variance increases both linearly with time t and faster along-track than in the cross-track directions.7The UAV predicted position XA(t)∈R3at time t is the n formulated by


Fig.2 Future position of a UAV,accounting for uncertainty.
where wA(t)=QA(t)ΣABA(t),with BA(t)a standard threedimensional Brownian motion starting from the origin whose variance is given by the matrix QA(t)ΣA∈ R3X3.In detail,is a diagonal matrix whose entriesandare the variance growth rates of the perturbation in the along-track and the two cross-track directions.They comply with the relationis an orthogonal matrix whose first columnis set as.Analogous models have been proposed in Refs.9,11,22for predicting future aircraft position over tens of minutes.
2.3.Measure of airspace safety
The safety envelope specifies the protected zone of a UAV.If other UAVs enter the safety envelope during the flight time interval[t0,t0+Δt],a conflict is considered to have occurred.Similarly,we define the event in which a space point X is in conflict with UAV A as point X entering the safety envelope of UAV A during the time interval[t0,t0+Δt].The conflict probability is denoted as

Assuming multiple UAVs Ai(i=1,2,...,N)are flying in the same airspace,the safety of the space point X is denoted as s(X).This is the probability that point X is in conflict with at least one UAV during the time interval[t0,t0+Δt].It also means that point X enters at least one UAV safety envelope.Then we have

Note that s(X)=0 means space point X will not be inside any of the existing UAV safety envelopes during the time interval[t0,t0+Δt].In addition,s(X)=1 signifies that space point X will enter at least one safety envelope of these UAVs during the time interval[t0,t0+Δt].s(X)indicates the degree of danger for space point X.When s(X)exceeds the specified threshold,point X is considered to be dangerous for new UAVs to enter during the time interval[t0,t0+Δt].
The probability that space point X enters the safety envelope of UAV Aiduring the time interval[t0,t0+Δt]is denoted as pAi(X).Assuming the Brownian motion affecting the future positions of these UAVs are independent,the safety situation s(X)satisfies

The problem of evaluating safety is reduced to that of estimating the conflict probability pAi(X).
2.4.Analysis of conflict probability
Generally,approaches to the calculation of pAi(X)take a great amount of computation.The computing time grows exponentially with the increase in the number of aircraft.7Now we will examine an approximate analytical model for the probability pAi(X),dropping the subscript of Aiin the following equations for ease of notation.

Fig.3Probability that X enters E(XA):P{X∈E(XA)t∈|[t0,t0+Δt].}.
The probability pA(X)considers the event where space point X enters the safety envelope E(XA)centered at XAwith a constant velocity vAand perturbation wA(t)during the time interval[t0,t0+Δt](see Fig.3).From the perspective of relative motion,if UAV A is considered to be stationary with only the perturbation wA(t),the n the safety envelope centered at X should move at a constant velocity-vAcontrary to UAV A(see Fig.4).Hence,E(XA)and E(X)have equal size but different centers.From Eq.(7),we have

With the assumption that UAV A is moving along a straight line of nominal trajectory with constant velocity,Eq.(6)can be rewritten as

The relative position ΔX(t)=X-XA(t)of UAV A with respect to the point X is given by


From Eq.(13),we can consider the motion of UAV A as consisting only of the perturbation wA(t)and the motion of space point X as determined by constant velocity Δv starting from ΔX0.Then,pA(X)is transformed as the probability that the perturbation wA(t)hits the safety envelope whose center is moving at a constant velocity for some t∈[t0,t0+Δt]:

Furthermore,wA(t)can be transformed to a standard three-dimensional Brownian motion by the following process.

Fig.4 Probability that XAenters E(X):P{XA∈ E(X)|t∈
Define the matrix F=QAΣA,and the vector φ =F-1Δv.Construct an orthogonal matrix P=[p1,p2,p3]∈R3X3with p1=-φ/‖φ‖,the n align the first column of P with -φ.Its inverse P-1=PTrepresents a rotation that makes the -φ/‖φ‖ direction coincide with the first coordinate axis direction:

Using transformation ΔZ(t)=P-1F-1ΔX(t),we transform Eq.(13)into


From Eq.(16),we take pA(X)as the probability that the standard Brownian motion^B(t)starting from the origin hits a moving safety envelope^E(Z)obtained by transforming E(ΔX0+ Δvt)in the new coordinate system.

where

The center of^E(Z)is moving at the constant velocity k starting from the position r.From the construction of matrix P,the velocity k is directed along the negative z1axis(see Fig.5).
Now the problem of evaluating pA(X)is transformed into a calculation of the probability that the Brownian motionenters the regionduring the time interval[t0,t0+Δt].
The probability density function of the three-dimensional standard Brownian motionis

The conflict probability is the integral of the probability density function in the safety envelope

Since the safety envelope is composed offour different quarter ellipsoids,the volume ofis calculated by


Fig.5 Transformed coordinates.
The radius of equivalent sphere reqis given as

Substituting Eqs.(1)and(22)into Eq.(23),we have

With the approximation of an equivalent sphere,the matrix M in Eq.(5)becomes

Substituting this expression into Eq.(19),we have

in the new coordinates(see Fig.6).
The center ofis moving at the constant velocity k starting from position r along the negative z1axis direction.An analytical approximation is the n presented for the probability in Eq.(18).pzis defined as the plane that passes through the center Z=r+kt of the sphereat some time instant t∈[t0,t0+Δt].Let pzbe orthogonal to the velocity k,the n pzdivides the sphereinto two equal parts.Projectingonto the plane pz,we obtain a circle Ezwith the radius req.Define Szas the minimum bounding square containing the projection circle Ezand Szhas a side length of 2req.
From the previous discussion,we define pA(X)as the probability that space point X enters the safety envelope E(XA)within[t0,t0+Δt],which is transformed as the probability that the Brownian motionstarting from the origin hits the spherewhose center moves in the negative z1axis direction starting from r at time t=0 s.A conflict occurs if and only ifever wanders into the moving sphere.Since it is difficult to get an analytical expression of such a probability,we approximate it by the probability of the event that,whenfirst hits the moving plane pz,the impact point is located inside the minimum bounding square Sz.

Fig.6 Regionreplaced by an equivalent sphere with radius req.
Usually the velocity k of the sphereis much larger than the variance growth rate of the Brownian motiontherefore only the dimension of the sphere perpendicular to k is relevant for the event mentioned above.A similar approximation was used to handle the problem in a two-dimensional case.11A formal discussion of the approximation error was reported.23Using the minimum bounding square Szin place of the projected circle Ezto calculate the probability pA(X)contributes to an over approximation and,at the same time,an over estimation of s(X).
In the new coordinate system,a negative r1lt;0 indicates that aircraft A is moving away from the space point X.That leads to a zero probability of X entering E(XA).When r1lt;0,we set pA(X)=0.
When r1≥ 0,the probability distribution of λ is characterized by the probability density function23

for any time T≥0 s,


The projection of the Brownian motionat the impact time λ on the plane pzis denoted asWhen λ =Th, the distribution ofis a twodimensional Gaussian random variable with zero mean and covariance ThI2.The probability density function ofis

At time λ =Th,the probability thatis located inside the minimum bounding square Szis calculated as

Defining l=r+kTh=[l1,l2,l3]T,the n the minimum bounding square is obtained by

From Eqs.(31)–(33),we have

Finally,an approximated expression for pA(X)can be written as

3.Airspace safety field
3.1.Effect of UAV flight performance on conflict probability
From the previous analysis,the safety envelope represents the safe separation requirement between UAVs.As a result of the approximation where we replace the safety envelopewith an equivalent sphere in Eq.(21),the equivalent radius reqcan be considered to characterize the safe separation requirement.Reviewing Eq.(24)in Section 2.3,

This is rewritten as

where V=[Vf,Vb,Va,Vd,Vl]Tis the state vector of UAV flight performance.For example,consider UAV A moves at a velocity vA=[5,0,0]Tkm/min from XA=[20,40,0]Tkm in the time frame[t0,t0+Δt]=[0,10]min.The UAV's maximum flight velocities are given as follows:
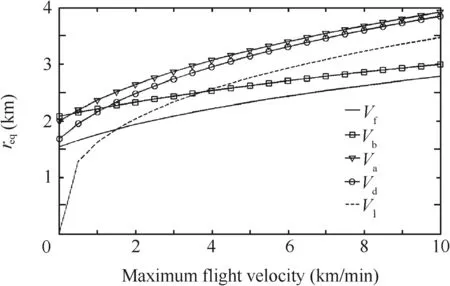
Fig.7 Variations of reqwith UAV flight performance.

Fig.8 Variations of reqwith response time τ.

Fig.9 Variations of conflict probability with UAV flight performance.

Fig.10 Variations of conflict probability with response time τ.

Fig.11 Airspace safety field in the horizontal plane with response time τ=1 min.

Fig.12 Airspace safety field in horizontal plane with response time τ=0.5 min.

In this way, the similar relations between reqand Vb,Va,Vd,Vl,τ can be derived.
In Fig.7,reqgrows when maximum flight velocity increases in any direction,although the growth rates are different.Fig.8 shows reqperforming a linear growth with response time.
Using first order approximation of Taylor expansion to expand Eq. (37) around the reference state V*=and τ*=60 s,we have

we have


Fig.13 UAV conflict resolution in horizontal plane.
Because of the bilateral symmetry of UAV flight performance,reqhas the same variation rate in the plane of symmetry,such that

But,the y are different in the plane of asymmetry.Generally,the velocities of a UAV in the horizontal plane arefaster than those in the vertical plane.reqis more sensitive to changes in vertical velocity.Hence,

In order to analyze the effect of UAV flight performance on conflict probability, considering a space point X=[55,35,0]Tkm,we obtain the conflict probability between UAV A and point X(see Fig.9).
Apparently,the conflict probability increases with maximum flight velocity in each direction.This is because the increase of maximum flight velocity enlarges the integral domain when calculating the conflict probability.
From Eq.(36),reqis of a linear growth rate with the response time τ around the reference state V*.The conflict probability also significantly increases with the response time τ.When τ=3 min,the safety envelope grows to three times that which would result in a certain conflict between UAV A and point X.The conflict probability pA(X)≈1.0(see Fig.10).
Taking the effect of UAV flight performance into consideration when determining safe separation will improve the utilization efficiency of airspace.According to Eq.(36),the safety envelope is variable for different UAVs and different response times.
3.2.Construction of airspace safety field
Supposing there are n UAVs existing in the airspace,we obtain the measure of airspace safety

If the parameters mentioned above are obtained,s(X)is determined.The increase of Vf,Vb,Va,Vd,Vland τ will result in a larger safety envelope and also a larger integral domain when computing the conflict probability pA(X).In Eq.(8),s(X)is obviously an increasing function of pA(X).If X varies over S,an airspace safety field can be constructed.Discretizing airspace S by using a uniform gridding of step size ρgt;0 along all axes,one can evaluate s(X)across S.The following examples are for illustration.
Fig.11(a)–(c)are the airspace safety fields in the horizontal plane during different time frames Ttf.In the simulation,two UAVs move in the horizontal plane at the same constant velocity v=4 km/min.They also have the same flight performance,with the maximum velocities given in Section 3.1.One UAV moves to east while the other moves northwest(the white dots and arrows denote the positions and directions of UAVs).Models of the safety field during three time frames[0,5]min,[5,10]min and[0,10]min are shown.In Fig.11,the red areas indicate the occupied region of a certain existing UAV,hence new entered UAVs should avoid passing through this area within the time frame Ttf.The blue area represents the free region of no existing UAVs.An intermediate color between red and blue signifies the degree of danger according to the magnitude of probability.In Fig.12,the response time is half of that in Fig.11,with a corresponding halving in size of the safety envelope.A smaller safety envelope means a smaller protected zone to avoid being penetrated.Therefore,the congested area of high conflict risk in Fig.12 is less than that of Fig.11.This is apparently observed in the airspace safety field.
The airspace safety field clearly shows the occupancy distribution of airspace.Constructing the safety fields for different consecutive time intervals can predict when UAVs enter and leave a certain zone in the airspace.This information can be used for detecting congested areas within time-space coordinates.The availability of airspace safety field can support UAV conflict resolution and trajectory planning.
4.Applications of airspace safety fields
4.1.Conflict resolution

Fig.14 Experiment site.

Fig.15 Trajectories of three UAVs.

Fig.16 Variations of safety fields in formation flight.
The airspace safety field is composed of the conflict probability in each discrete point after the airspace was discretized.When airspace safety conditions around a UAV in the future time interval[0,t]is obtained,UAV conflict resolution can be performed.Usually,there are four kinds of maneuvering for UAV flight conflicts:left turn or right turn in the horizontal plane and climbing or descending in vertical plane.In Fig.13,take the safety of the horizontal plane as an example.Suppose a UAV is flying at a constant velocity,and X=[x,y]Tis the UAV's current position.Z is the set of integers.The conflict probability p(Xi,j)indicates the safety of point Xi,jand can be calculated by Eq.(35).Denote Sforwardas the unit area in front of the UAV.Similarly,Sleftis the front-left unit area of the UAV and Srightis the front-right unit area of the UAV(see Fig.13).If p(Sforward)is the conflict probability of the unit area in front of the UAV,we have

In the same way,we have


Define p0as the threshold of conflict probability.Ifthe UAV maintains forward flight.Ifa conflict alert is given.Comparing p(Sleft)and p(Sright),if p(Sleft)lt;p(Sright),the UAV changes heading and performs a left-turn maneuver,otherwise it performs a right-turn maneuver.
The same principle applies in a three-dimensional case.Define Saboveas the front-above unit area of the UAV and Sbelowas the front-below unit area of the UAV.When a conflict occurs,maneuvering in horizontal plane is considered preferable.If p(Sforward)≥p0,p(Sleft)≥p0and p(Sright)≥p0,it means the conflict cannot be solved in the horizontal plane.Comparing p(Sabove)and p(Sbelow),if p(Sabove)lt;p(Sbelow),the UAV performs a climbing maneuver,otherwise it performs a descending maneuver.
To illustrate the validity of airspace safety construction and the conflict resolution method,an experiment of UAV formation flying with obstacle avoidance is performed.Since power lines and towers are some of the most dangerous obstacles in low altitude airspace,a dried-up riverbed is chosen as the experiment site.We constructed three artificial poles in a triangle and joined the three peaks with power lines to simulate obstacles(see Fig.14).
Fig.15 shows the trajectories that UAVs use to avoid the artificial obstacle.Three UAVs fly from east to west in the horizontal plane with the altitude H=15 m.The red area in the center of Fig.18 indicates the addition of the artificial poles into the safety field.
Fig.16 illustrates the variations of safety fields in formation flight.UAVs take off at time t=0 s.Five different moments at 5,17,25,30 and 38 s are chosen to determine the safety field.The time variants and tendencies of the safety field can easily be observed.The heading changes made by UAVs when performing conflict resolution can also be observed.
4.2.Trajectory planning
Consider that UAV B enters the airspace region S where other UAVs are flying.UAV B starts from the entry point at time 0 s to the destination before time T at a constant velocity.The predetermined trajectory of UAV B is a straight line.However,as a result of the presence of other UAVs,this trajectory is not ensured to be of low conflict risk.UAV B can pick a fixed number m of direction changes at specified points in time 0lt;t1lt;t2lt;...lt;tmlt;t.
The problem of finding an optimal trajectory that minimizes the sum of the total flight time and the conflict risk along its current trajectory is formulated as

where J is a weighted sum of the total flight time Tnand the conflict risk along its trajectory;z is the trajectory of UAV B;dnis the total distance of the trajectory;vBis the velocity of UAV B and η is the weight coefficient.The first term of cost function J shows the economic requirement that UAV B needs to fly through the airspace as quickly as possible.The second term represents the safety requirement that the conflict risk along the trajectory must be as low as possible.

Fig.17 Nominal trajectories and velocities of five UAVs.

Table 1 Parameters used in example.
In the computation of s(X),the trajectory is discretized by m waypoints.Therefore,the sum of the conflict risk of the waypoints p1,p2,...,pmis taken as a measure of the conflict risk along its trajectory.The cost function J reduces to

This problem can be easily solved by the sequential quadratic programming (SQP) method,which has proven highly effective for solving constrained optimization problems with smooth nonlinear functions in the objectives and constraints.24In this example,the predetermined straight trajectory is taken as the initial condition for the solution.Because the velocity of UAV B is constant,a smaller η means the less deviation of predetermined trajectory and less flight time.A bigger η contributes a greater priority to the low conflict risk requirement and leads to a less conflict-prone trajectory for safety.

Fig.18 Safety field and optimal trajectories in horizontal plane.

Fig.19 Length of optimal trajectory of 0,5 and 10 km high planes.
Supposing that five UAVs are moving in a three dimensional airspace region and each UAV is flying at constant velocity along a straight line during the time interval T.The nominal trajectories of UAVs are shown in Fig.17.
The uncertainty that affects UAV future positions is characterized byandThe number of waypoints is taken as m=99(the start point and the end point are not included).UAV B has to fly through the airspace region in 15 min at a constant velocity.The entry point and destination point of UAV B are X0and XD.UAV B can change its direction only on the horizontal plane.All the parameters used in the example are given in Table 1.
Fig.18(a)shows the airspace safety field and optimal trajectory of UAVB on the horizontal plane of H=0 km high.When UAV B needs to go through the airspace region as soon as possible,trajectory 1 will be optimal,but this trajectory is at risk for conflict with other UAVs.In contrast,trajectory 2 is more safe,although it takes more time.However,there is a trade off between efficiency and safety that depends on the choice of appropriate weight coefficient η.Fig.18(b)and(c)show the cases of H=5 km high and H=10 km high,respectively.
Fig.19 shows that the length of all three optimal trajectories increase when the weight coefficient η grows.Obviously,the higher η denotes greater safety requirements and leads to a longer trajectory.UAVs need to avoid approaching the congested regions of high conflict risk,which results in more deviation in predetermined trajectory.
5.Conclusions
(1)The safety envelope is a variable-size protected zone for different UAVs.In a predetermined response time,the conflict probability increases with the maximum flight velocity of UAV in each direction.
(2)Based on the uncertainty of UAV positions in the future,a probabilistic approach is presented to evaluate the conflict probability between a space point and the UAV safety envelope in a mid-term horizon.With the assumption of equivalent spheres,an analytical approximation of the conflict probability is derived.
(3)The airspace safety field is constructed to indicate the occupancy distribution of airspace.This information can be used for UAV conflict resolution and trajectory planning of newly entering UAVs.
Acknowledgement
This work was supported by the National Basic Research Program of China(No.2011CB707002).
1.Zhang J.New development and application of airspace surveillance technology.Acta Aeronaut Astronaut Sin 2011;32(1):1–14[Chinese].
2.Reich PG.Analysis of long-range air traffic systems:separation standards I.J Navigation 1966;19(1):88–98.
3.Reich PG.Analysis of long-range air traffic systems:separation standards II.J Navigation 1966;19(2):169–86.
4.Reich PG.Analysis of long-range air traffic systems:separation standards III.J Navigation 1966;19(3):331–47.
9.Paielli RA,Erzberger H.Conflict probability estimation for free flight.J Guid Control Dyn 1997;20(3):588–96.
10.Yang LC,Kuchar JK.Prototype conflict alerting system for free flight.J Guid Control Dyn 1997;20(4):768–73.
5.Brooker P.Lateral collision risk in air traffic system:A 'Post-REICH' event model.J Navigation 2003;56(3):399–409.
6.Kopardekar P,Schwartz A,Magyarits S,Rhodes J.Airspace complexity measurement:An air traffic control simulation analysis.Int J Indust Eng-Theory Appl Pract 2009;16(1):61–70.
7.Sridhar B,Sheth KS,Grabbe S.Airspace complexity and its application in air traffic management.Proceedings of the 2nd USA/Europe air traffic management Ramp;D semina;1998 Dec 1–4;Orlando(FL).Brussels,Belgium:Eurocontrol Press;1999.
8.Prandini M,Putta V,Hu JH.A probabilistic measure of air traffic complexity in 3-D airspace.Int J Adapt Control Sig Process 2010;24(10):813–29.
11.Prandini M,Hu JH,Lygeros J,Sastry S.A probabilistic approach to aircraft conflict detection.IEEE Trans Intell Transport Syst,Spec Iss Air Traffic Control-Part I 2000;1(4):199–220.
12.Hu JH,Prandini M,Sastry S.Aircraft conflict prediction in the presence of a spatially correlated wind field.IEEE Trans Intell Transport Syst 2005;16(3):326–40.
13.Jackson JA,Boskovic JD.Application of airspace encounter model for prediction of intruder dynamics.AIAA modeling and simulation technologies conference;2012 Aug 13–16;Minneapolis(MN).Reston:AIAA;2012.p.985–1004.
14.Blom HAP,Bakker GJ.Conflict probability and incrossing probability in air traffic management.Proceedings of the 41st IEEE conference on decision and control;2002 Dec 10–13;Las Vegas (NV).Piscataway (NJ):IEEE Press;2003.p.2421–6.
15.Blom HAP,Krystul J,Bakker GJ,Klompstra MB,Klein Obbink BK.Free flight collision risk estimation by sequential Monte Carlo simulation.Stochastic Hybrid Systems.Tayloramp;Francis/CRC Press;2007.p.249–81.
16.Visintini AL,Glover W,Lygeros J,Maciejowski J.Monte Carlo optimization for conflict resolution in air traffic control.IEEE Trans Intell Transport Syst 2006;7(4):470–82.
17.Lygeros J.On reachability and minimum cost optimal control.Automatica 2004;40(6):917–27.
18.Mitchell I,Bayen A,Tomlin C.A time-dependent Hamilton-Jacobi formulation of reachable sets for continuous dynamic games.IEEE Trans Autom Control 2005;50(7):947–57.
19.Gillula JH,Huang HM,Vitus MP,Tomlin CJ.Design of guaranteed safe maneuvers using reachable sets:Autonomous quadrotor aerobatics in theory and practice.Proceedings of 2010 IEEE international conference on robotics and automation;2010 May 3–8;Anchorage(AK).Piscataway(NJ):IEEE Press;2010.p.1649–54.
20.Greatwood C,Richards A.Minimal sensor scanning volumes for helicopter terrain avoidance.AIAA guidance,navigation and control conference;2010 Aug 2–5;Toronto.Reston:AIAA;2010.p.1–8.
21.Zhuang NJ,Luo ZP,Ren YR,Xiang JW.Fast calculation method for helicopter reachable domain in forward flight.J Beijing Univ Aeronaut Astronaut 2014;40(6):810–4[Chinese].
22.Erzberger H,Paielli RA,Isaacson DR,Eshow MM.Conflict detection and resolution in the presence of prediction error.Proceedings of the 1st USA/Europe air traffic management Ramp;D seminar;1997 Jun 17–20;Saday,France.Brussels,Belgium:Eurocontrol Press;1997.
23.Hu JH.A study of conflict detection and resolution in free flight[dissertation].Berkeley:University of California at Berkeley;1999.
24.Gill PE,Murray W,Saunders MA.SNOPT:An SQP algorithm for large-scale constrained optimization.SIAM J Optimiz 2006;12(4):979–1006.
Xiang Jinwuis a professor and Ph.D.supervisor at the School of Aeronautic Science and Engineering,Beihang University,Beijing,China.He received his Ph.D.from Nanjing University of Aeronautics and Astronautics in 1993.His current research interests include UAV systems,aircraft dynamics and control.
Liu Yangis a Ph.D.student at the School of Aeronautic Science and Engineering,Beihang University,Beijing,China.His areas of research include aircraft trajectory optimization and conflict detection and resolution.
Luo Zhangpingis an associate professor and master student supervisor at the School of Aeronautic Science and Engineering,Beihang University,Beijing,China.He received his Ph.D.from Beihang University in 2004.His current research interests include flight safety,aircraft dynamics and control.
2 September 2015;revised 18 November 2015;accepted 15 June 2016
Available online 27 August 2016
Airspace safety situation;
Conflict probability;
Flight conflict;
Navigation;
UAV
©2016 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.Tel.:+86 10 82315530.
E-mail addresses:xiangjw@buaa.edu.cn(J.Xiang),youngka@126.com(Y.Liu),luozp@buaa.edu.cn(Z.Luo).
Peer review under responsibility of Editorial Committee of CJA.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Flapping wing micro-aerial-vehicle:Kinematics,membranes,and flapping mechanisms of ornithopter and insect flight
- A new non-linear vortex lattice method:Applications to wing aerodynamic optimizations
- Experimental study of flow field distribution over a generic cranked double delta wing
- Streamwise-body-force-model for rapid simulation combining internal and external flow fields
- An artificial neural network approach for aerodynamic performance retention in airframe noise reduction design of a 3D swept wing model
- effects of wing locations on wing rock induced by forebody vortices
