Wing aeroelasticity analysis based on an integral boundary-layer method coupled with Euler solver
2016-11-24MaYanfengHeErmingZengXianangLiJunjie
Ma Yanfeng,He Erming,Zeng Xianang,Li Junjie
aSchool of Aeronautics,Northwestern Polytechnical University,Xi'an,Shaanxi 710072,China
bAVIC Xi'an Aircraft Design and Research Institute,Xi'an,Shaanxi 710089,China
Wing aeroelasticity analysis based on an integral boundary-layer method coupled with Euler solver
Ma Yanfenga,b,He Erminga,*,Zeng Xianangb,Li Junjieb
aSchool of Aeronautics,Northwestern Polytechnical University,Xi'an,Shaanxi 710072,China
bAVIC Xi'an Aircraft Design and Research Institute,Xi'an,Shaanxi 710089,China
An interactive boundary-layer method,which solves the unsteady flow,is developed for aeroelastic computation in the time domain.The coupled method combines the Euler solver with the integral boundary-layer solver(Euler/BL)in a''semi-inversequot;manner to compute flows with the inviscid and viscous interaction.Unsteady boundary conditions on moving surfaces are taken into account by utilizing the approximate small-perturbation method without moving the computational grids.The steady and unsteady flow calculations for the LANN wing are presented.The wing tip displacement of high Reynolds number aero-structural dynamics (HIRENASD) Project is simulated under different angles of attack.The flutter-boundary predictions for the AGARD 445.6 wing are provided.The results of the interactive boundary-layer method are compared with those of the Euler method and experimental data.The study shows that viscous effects are significant for these cases and the further data analysis confirms the validity and practicability of the coupled method.
1.Introduction
Aeroelasticity is a multidisciplinary problem involving the interaction among inertial,elastic and aerodynamic forces,and plays an important role in aircraft design and qualificationprocess.1The standard industry analysis methods for flutter prediction of aerospace structures include time-domain and frequency-domain analysis.The frequency-domain method2is widely used for the practical design analysis in industry because of its high efficiency and easiness in setting up the aero model,while its limitedness is in handling transonic and other nonlinear flows.
For the nonlinear transonic flutter problems,where the linearized aerodynamic methods become less applicable,it is essential to model a full unsteady aerodynamic system generated by shock wave movements.At present,these problems can be mostly solved by Euler or Navier-Stokes methods.3–5A flow solver with Navier-Stokes equations includes the effect of the viscosity,but it requires undesirably large amount of computational resources.On the other hand,an Euler solver captures all the flow characteristics of the transonic flow except viscous effects.In order to take into account the viscous effects and reduce computational costs,an integral boundary-layer coupling method(Euler/BL)can be used,which provides a good balance between the precision of the flow model and the computational efficiency.6Due to the well-known Goldstein singularity,7several interactive boundary-layer coupling techniques are developed including the fully quasi simultaneous,quasi simultaneous and semi-inverse methods.8Most of the m focus on steady calculations.9–12The semi-inverse coupling method was proposed by Carter.13This method was extensively used by Cebeci and his colleagues with inviscid panel methods and even Euler solver.14Zhang and Liu et al.employed the semi-inverse method in the calculation of unsteady flow and flutter.6,15,16
For computational aeroelasticity analysis,the accurate information exchange and coupled model between the fluid and structure module are also very important in order to obtain correct results.The methods of infinite plate spline (IPS) and beam spline are widely used by software programs such as PATRAN/NASTRAN.17Loosely coupled models are very popular for computational aeroelasticity,18in which the structure and fluid solutions are determined separately and each treats the interaction effects as external disturbances.This loosely coupled procedure is easy to implement and demands low-cost computing resources.Consequently,the interpolation techniques of IPS and the loosely coupled models are used in this study.
Firstly,the coupled method of Euler with integral boundary-layer(Euler/BL)is developed in a''semi-inversequot;manner.And its applications to the solution procedures of static aeroelasticity and flutter are also shown.The proposed procedures are applied to the calculation of unsteady transonic flow and aeroelastic problems around a wing.The results are compared with those from Euler solver and experimental data,and further data analysis demonstrates the proposed method's validity and practicability in industry.
2.Computation scheme
2.1.Euler equations
The governing equation for the three-dimensional Euler equations in integral is given as

where V denotes a control volume bounded by surface S.The dependent variable Ω and the flux vectorare given by

where p,ρ,E,and~H denote the pressure,density,total energy and total enthalpy,respectively,while u,v and w are the velocity components.For a perfect gas of specific heat ratio γ,the total energy is given by

while the total enthalpy is given by

The three-dimensional Euler equations are solved on the structural grids by using the cell-centered finite-volume for spatial discretization.The dual-time stepping technique is applied,which combines the advantages of both implicit methods and fast solving techniques.For unsteady Euler computation,the use of moving or deforming grids can be a rather time consuming and nontrivial task for practical applications.To avoid the tedious process of grid regenerations,a small perturbation boundary treatment(Transpiration Boundary Condition)has been employed as proposed by Liu et al.6,15,16
2.2.Integral boundary-layer method
The Euler/BL equations are used as the governing equations in addition to the Euler equations and applied to the calculation of the steady and unsteady flows.
2.2.1.Laminar boundary-layer
The Cohen-Reshotko method19is used to solve the laminar boundary-layer.It involves the momentum integral equation for compressible laminar cases with arbitrary pressure gradient and heat transfer.It is one of the most accurate,programmable general methods available for the laminar case and can be found in Refs.19,20.
2.2.2.Transition
Transition is specified or determined using Michel's formula6:

In the case of high Reynolds number,laminar boundarylayer is very thin and close to stagnation point region.To solve such problem,a fixed forced-transition is set on 3%–5%of local chord without Michel's formula.
2.2.3.Turbulent boundary-layer
The momentum equation is

where Cfis the skin-friction coefficient;θ is the boundary-layer momentum thicknesses;s is the streamwise coordinate along the airfoil wall or wake;H is the shape factor;Ueand Meare local air velocity and mach number at the boundarylayer edge.
Head introduced the entrainment coefficient CE:

where ρeis local air density at the boundary-layer edge;H1is the Head's shape factor;is the kinematic shape factor.
The two Eqs.(6)and(7)can be combined into a 2X2-system for the unknowns θ andWhenis immediately clear that the matrix is singular and this is the well-known Goldstein singularity.7The flow separation occurs and boundary-layer becomes turbulent from the transition point.As a result,the continuity Eq.(8)and Green's lag Eq.(9)are introduced to avoid Goldstein singularity:
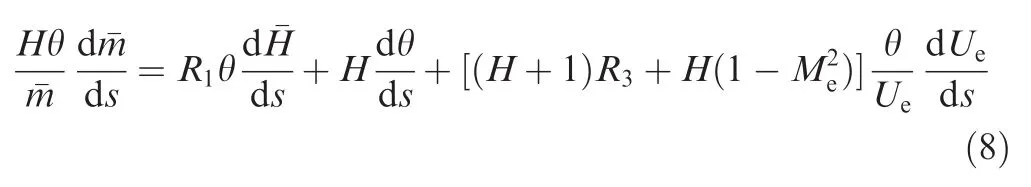
where R1,R2and R3are three parameters which are related to the ratio of specific heats γ,temperature recovery factor r,and the local boundary-layer edge Mach number Me:

where Cτis the shear stress coefficient,λ is a parameter to account for secondary effects,¯F is also a parameter to be defined in Green's paper.6The subscript EQ denotes quantities evaluated under equilibrium conditions where the shape factor and the entrainment coefficient are invariant,while EQ0 denotes quantities evaluated under equilibrium flow free of secondary effects.
Therefore,a linear system of Eqs.(6)–(9)is obtained for the four unknown boundary-layer derivative parameters:andtotally.The correlations of various parameters in the four equations can be found in Ref.6.These equations can be written in the following matrix form:

where

The eigenvalues of the matrix Eq.(10)are considered by the first third-order matrix because θgt;0.In the turbulent flow,and(R3-H)lt;0,so eigenvalues can be obtained by Eq.(12)and are always positive.
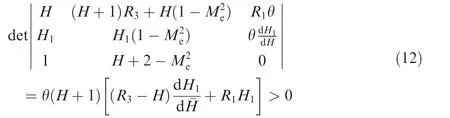
Theformulas for solving the four unknown variables are given:

The interaction-law has been formulated for twodimensional model and can be extended to three dimensions.The three-dimensional lifting surface is divided into slips along the flow direction and the flow is ignored on spanwise wing.This approach is feasible for high-aspect-ratio wing.
The schematic figures are shown in Fig.1 and the inviscidviscous coupling procedures are as follows:

Fig.1 Schematic diagram of inviscid-viscous coupled computation.
(1)Initial thickness of boundary-layer distribution δ*(s)is given in advance.The Eqs.(13)–(16)are employed to solve each boundary-layer variable¯H,θ,and Uev.
(2)The blowing velocity Vbcan be obtained from mass conservation:

The blowing velocity Vbis used considering the viscous effect in the Euler solver,which is implemented as the simplified boundary condition6for the unsteady and aeroelastic computations.
(3)The outer boundary-layer speed Ueiis solved by Euler equations after 15–50 iteration steps.
(4)The boundary-layer thickness is updated by relaxation scheme:
Carter's formula:
Edward's formula:

Here,ω is an under-relaxation factor and is usually taken 0.1–0.2.Each of the two relaxation schemes has its own advantages and disadvantages,so users need to choose according to different models and calculating states.The Carter's scheme converges quickly,but the calculation stability is not high and easy to diverge on the separation flow.The Edward's scheme is more stable,but relatively has slow convergence speed.So we can first apply the Carter's scheme to a small residual value,and the n use Edward's scheme until it converges.

2.3.Solution procedure for static aeroelastic analyses
The dynamic response of structure is analyzed by the mode superposition method.The motion of forced vibration of multi-degree-of-freedom system can be obtained from the physical characteristics of the system:

where M is the generalized mass matrix;K is the generalized stiffness matrix;F is the generalized aerodynamic force matrix;q is the generalized displacement.
Furthermore,an iterative procedure Eqs.(21)–(25)can be used to get an updated generalized force F:


where Φ is the displacement interpolation matrix from structure grids to aerodynamic grids;Q∞is the dynamic pressure;f(d(j),α)is the force vector of aerodynamic model's surface grid.
The iterative process must be iterated untilis equal to desired tolerance.is relaxation factor and 0.2–0.6 is chosen to ensure iteration converge.If it does not converge no matter how smallis,the n the analysis of static aeroelasticity is divergent.
2.4.Solution procedure for flutter analyses
Eq.(20)is also applied to solving the flutter problem.We introduce the state-space variables X=[q,˙q]T,and Eq.(20)can be rewritten in state-space form:

The Runge-Kutta method is applied to solving the differential Eq.(26)and its expansion is given by

When computations are performed on a loosely coupled model,the aerodynamic forces F(Xn+k1/2,tn+Δt/2)and F(Xn+k2/2,tn+Δt/2)are unknowns except F(Xn,tn).If these unknowns are substituted by F(Xn,tn),the coupled method is only offirst-order time accuracy.Therefore,the time step must keep small enough to satisfy the accuracy requirement.
The aerodynamic forces Ft-2Δt,Ft-Δtand Ft(at time steps t-2Δt,t-Δt and t)can befitting out a quadratic curve,so that the numerical extrapolated method is employed at time t+Δt/2 and t+Δt:

Substituting Eq.(28)into the equation for the Runge-Kutta expansion,Eq.(27),yields

The Eq.(29)provides second-order time accuracy and the time step can be increased moderately,which can improve the efficiency of the computation.21Loosely coupled solution scheme can be seen as a serial staggered procedure for flutter analyses in Fig.2,in which qtis the generalized displacement and Vtbis the blowing velocity at time steps t.

Fig.2 Iterative solution scheme for flutter analyses.

Fig.3 LANN wing aerodynamic grids.
Step 1.The fluid calculation results are taken as loads exerted on the structure,and the corresponding forces at nodes between fluid and structure are exerted on the FE model by interpolation techniques.
Step 2.Eq.(29)is solved numerically to update the generalized displacement values qnat the time step.
Step 3.The displacements resulting from the solution of the structural equations deform the aerodynamic surface grid(using the coupling scheme)and,as a consequence,change the boundary conditions for the next aerodynamic solution step.
Step 4.The fluid state equations are solved under updated wall boundary condition.This step determines the solution vector of the fluid and also a new pressure distribution for the deformed state.
Step 5.Repeat Steps 1–4 using current solution as the initial value for the subsequent steps.

Fig.4 Comparison of steady pressure distributions.
3.Static aeroelastic calculation and analysis
3.1.Steady flow validation
The sections of the LANN wing are supercritical airfoils from the AGARD R-702 report.The wing is twisted from 2.6°at the root section and-2°at the tip section.The aspect ratio of the wing is 7.92.The taper ratio is 0.4 and the quarter-chord swept angle is 25°.22C–H grids are used for the Euler and Euler/BL computations which totally include 527,280 spatial grids and 1960 surface grids as shown in Fig.3.
The steady flow field is computed and used as the initial flow field for the unsteady computation.The Mach number Ma is 0.822;the angle of attack α is 0.6;the experimental Reynolds number based on root chord is 20.27X106.Fig.4 shows the comparisons of the calculated and experimental surface pressures,where b is the half span.The results obtained from the current Euler/BL method are fairly consistent with the experimental data.The shock position is shifted forward and the strength is weakened compared with the Euler solutions.
3.2.HIRENASD wing finite element model and structured grids of flow field

Fig.5 HIRENASD schematic structure of finite element model.

Fig.6 HIRENASD wing aerodynamic grids.
The high Reynolds number aero-structural dynamics (HIRENASD) project23,24was led by the Aachen University with funding from the German Research Foundation.It was initiated in 2004 to produce a high-quality transonic aeroelastic data set at realistic flight Reynolds numbers for a large transport-type wing/body configuration and tested in the European transonic wind tunnel (ETW) in 2006.Therefore,detailed experimental data can be provided for static aeroelastic validation of this study.
The finite element model(FEM)of the HIRENASD wing is modeled with solid elements and composed of NASTRAN hexagonal elements with over 200,000 grid points as shown in Fig.5.The first ten oscillating frequencies and oscillating modes are chosen for calculation.
The flow field of the spatial grids and surface grids about the HIRENASD wing is shown in Fig.6.The number of spatial grids is 855,108 and that of surface grids is 7750.
3.3.Static aeroelastic results and analysis
As mentioned in Section 2,the iterative process Eqs.(21)–(25)is applied to calculating static aeroelastic deformation of the wing(Ma=0.80,α=1.5 and Re=7X106).The HIRENASD experimental steady pressure data are collected at six span sections,which are identified in Fig.7.Fig.8 presents the distribution pressure coefficient(Cp)results at six sections obtained from the rigid steady(undeformed)and static aeroelastic(deformed)solutions.The trend of Cpis consistent with the experimental results and deformed surface pressure is closer to the experimental values than that in the rigid case.
The wing tip displacements are calculated at five angles of attack(-1.5°,0.0°,1.5°,3.0°and 4.5°)and compared with experimental data shown in Fig.9.25,26The calculated displacements for HIRENASD are slightly less than experimental data.
The analysis of static aeroelasticity based on an integral boundary-layer method is developed.The results show that:
(1)Deformed pressure distributions are more consistent with experimental results.
(2)Compared with the experimental data,the process of static aeroelasticity is feasible and can be used for high-aspect-ratio wing.

Fig.7 HIRENASD span sections 1–6.

Fig.8 Comparison of rigid steady and static aeroelastic surface pressure distributions.

Fig.9 Wing tip displacements for HIRENASD,Ma=0.8,Re=7 million.
4.Flutter calculation and analysis
4.1.Unsteady flow validation
The LANN wing is also used to test the accuracy in unsteady case.The wing oscillates around an upswept axis at 62.1%of the root chord in a pitch motion as

In this case,the mean angle of attack α0is 0.6;the pitching amplitude αmis 0.25;the reduced frequency κ is 0.204.In order to compare the pressure distribution of the unsteady computation,the Fourier transformation is used.The first mode of the normalized pressure distribution at six span positions is shown in Fig.10.

Fig.10 Comparison of unsteady pressure distributions.
Similar to the results of steady computation,the Euler solver over-predicts the shock wave position.The abrupt change can be seen in the unsteady pressure distributions at every position in Fig.10,corresponding to the position of the shock wave in Fig.4,where the shock wave changes the unsteady flow.The Euler/BL method well compensates the shortcomings that viscosity cannot be considered in Euler equations.When the shock wave appears on the surface of wing,the unsteady pressure distributions will bulge.
4.2.AGARD 445.6 wing
The AGARD 445.6 wing was tested in the NASA Langley Transonic Dynamics Tunnel(TDT)in 1961.Flutter data from this test have been publicly available for over 20 years and have been widely used for preliminary computational aeroelastic benchmarking.In this section,the results of the AGARD 445.6 wing are presented in order to validate the Euler/BL method for flutter calculations.The wing is semi-span with a quarter-chord sweep angle of 45°,an aspect ratio of 1.65,a taper ratio of 0.66,and a NACA 65A004 airfoil section which is a symmetric airfoil.27Its detailed parameters can be obtained in wind tunnel test report and the first four order oscillating modes were used in flutter analysis.

Fig.10(continued)

Fig.11 AGARD 445.6 wing aerodynamic grids.

Fig.12 Time histories of generalised displacements of AGARD 445.6 wing at Ma=0.901.
The surface grids of AGARD 445.6 wing and the structural computational grids are depicted in Fig.11.The spatial grids are 237,600;the surface grids are 24,192.
4.3.Flutter results and analysis
In order to illustrate the effect of boundary-layer correction,two methods are employed to calculate flutter of AGARD 445.6 wing at free stream(Ma=0.500,0.678,0.901,0.960,1.072 and 1.141).Moreover,the generalized displacements computed by the Euler method at Ma=0.901 are shown in Fig.12.Fig.13 presents comparisons of the experimental flutter speeds and frequency ratio values and N-S solver results obtained using the FUN3D code27are also compared.
The analysis of flutter based on an integral boundary-layer method is developed:
(1)The calculation results of three methods are consistent with the transonic dip of AGARD 445.6 wing near Ma=0.960;
(2)The results of the Euler/BL method are better than those of the Euler solver and less than those of N-S methods;however,the calculation is more efficient than that of NS equations.It is thus more suitable for industrial design environment.
5.Conclusions
An Euler/BL method has been developed to calculate unsteady flow and aeroelastic problems in detail.Three examples are presented to demonstrate the approach and the following conclusions can be drawn:
(1)The study firstly shows that the results obtained by the Euler/BL method are better than the Euler results in both steady and unsteady cases.
(2)A process of static aeroelastic analysis is verified,which is implemented on the HIRENASD wing.The development of flutter process is also verified by the AGARD 445.6 wing.
(3)It is concluded that the viscous effects are significant for these cases and further data analysis demonstrates the presented method's validity and practicability.The method can be used to solve aeroelastic problems.
Acknowledgements
This study was co-supported by the National Natural Science Foundation of China(No.51675426)and Aerospace Science and Technology Innovation Fund of China (No.2014KC010043).
1.Dowell EH,Hall KC.Modeling of fluid-structure interaction.Annu Rev Fluid Mech 2001;33(1):445–90.
2.Chen PC,Liu DD,Karpel M.ZAERO User's Manual.ZONA Technology;2006.p.1–10.
3.Tang L,Bartels R,Chen P,Liu DD.Numerical investigation of transonic limit oscillations of a 2-D supercritical wing.Reston:AIAA;2001.Report No.:AIAA-2001-1290.
4.Thomas JP,Dowell EH,Hall KC.Nonlinear in viscid aerodynamic effects on transonic divergence,flutter,and limit-cycle oscillations.AIAA J 2002;40(4):638–46.
5.Geissler W.Numerical study of buffet and transonic flutter on the NLR 7301 airfoil.Aerosp Sci Technol 2003;7(7):540–50.
6.Zhang ZC,Liu F.Calculations of unsteady flow and flutter by an Euler and integral boundary-layer method on Cartesian grids.Proceedings of the 22nd applied aerodynamics conference and exhibit;2004 August 16–19;Rhode Island,USA.Reston:AIAA;2004.p.1–13.
7.Lock RC,Williams BR.Viscous-inviscid interactions in external aerodynamics.Prog Aerosp Sci 1987;24(2):51–171.
8.Sturdza P,Suzuki Y,Martins-rivas H,Rodriguez DL.A quasisimultaneous interactive boundary-layer model for a cartesian euler solver.Proceedings of the 50th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition;2012 January 09–12;Nashville,USA.Reston:AIAA;2012.p.1–20.
9.Rodriguez DL,Sturdza P.Improving the accuracy of euler/boundary-layer solvers with anisotropic diffusion methods.Proceedings of the 50th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition;2012 January 09–12;Nashville,USA.Reston:AIAA;2012.p.1–15.
10.Drela M.Three-dimensional integral boundary layer formulation for general configurations.Proceedings of the 21st AIAA computational fluid dynamics conference;2013 June 27–30;San Diego,USA.Reston:AIAA;2013.p.1–24.
11.Nishida B,Drela M.Fully simultaneous coupling for threedimensional viscous/inviscid flows.Reston:AIAA;1995.Report No.:AIAA-95-1806.
12.Veldman AEP.A simple interaction law for viscous-inviscid interaction.J Eng Math 2009;65(4):367–83.
13.Carter JE.A new boundary-layer inviscid iteration technique for separated flow.Reston:AIAA;1979.Report No.:AIAA-1979-1450.
14.Potsdam MA.An unstructured mesh Euler and interactive boundary layer method for complex configurations.Reston:AIAA;1994.Report No.:AIAA-94-1844.
15.Gao C,Luo S,Liu F,Schuster DM.Calculation of unsteady transonic flow by an Euler method with small perturbation boundary conditions.In:Proceedings of the 41st aerospace sciences meeting and exhibit;2003 January 6–9;Reno,USA.Reston:AIAA;2003.p.1–13.
16.Gao C,Yang S,Luo S,Liu F,Schuster DM.Calculation of airfoil flutter by an Euler method with approximate boundary conditions.AIAA J 2005;43(2):295–305.
17.Rodden WP,Johnson EH.MSC/NASTRAN Aeroelastic analysis user's guide,Version 68.Los Angeles:The Macneal-Schwender Corporation;1994.
18.Relvasa A,Suleman A.Fluid–structure interaction modelling of nonlinear aeroelastic structures using the finite element corotational theory.J Fluid Struct 2006;22(1):59–75.
19.Cohen CB,Cresci RJ.The compressible laminar boundary layer with heat transfer and pressure gradient.Washington,D.C.:NASA;1956.Report No.:NACA TR-1294.
20.McNally WD,FORTRAN Program for calculating compressible laminar and turbulent boundary-layers in arbitrary pressure gradients.Washington D.C.:NASA;1979.Report No.:NASA TND-5681.
21.Zhang WW.efficient analysis for aeroelasticity based on computational fluid dynamics.[dissertation]Xi'an:Northwestern Polytechnical University;2006(Chinese).
22.Zwaan R.LANN wing pitching oscillation,compendium of unsteady aerodynamics measurements.London RH:AGARD;1982.Report No.:AGARD-R-702.
23.Acar P,Nikbay M.Steady and unsteady aeroelastic computations of HIRENASD wing for low and high Reynolds numbers.Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics,and materials conference;2013 April 8–11;Boston,USA.Reston:AIAA;2013.p.1–16.
24.Chwalowski P,Florance JP.Heeg J,Wieseman CD,Perry B.Preliminary computational analysis of the (HIRENASD) configuration in preparation for the aeroelastic predication workshop.International forum of aeroelasticity and structural dynamics;2011 June 26–30;Paris,France.2012.p.1–21.
25.Ritter M.Static and forced motion aeroelastic simulations of the HIRENASD wind tunnel model.Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics and materials conference;2012 April 23–26;Honolulu,USA.Reston:AIAA;2012.p.1–14.
26.Ballmann J,Dafnis A,Korsch H,Buxel C,Reimerdes HG.Experiment analysis of high Reynolds number aero-structural dynamics in ETW.Proceedings of the 46th AIAA aerospace sciences meeting and exhibit;2008 January 7–10;Reno,USA.Reston:AIAA;2008.p.1–15.
27.Lee-Rausch EM,Batinaf JT.Wing flutter computations using an aerodynamic model based on the Navier-Stokes equations.J Aircr 1996;33(6):1139–47.
Ma Yanfengis a Ph.D.student at School of Aeronautics,Northwestern Polytechnical University.Her area of research is aircraft aeroelasticity.
He Ermingis a currently professor at School of Aeronautics,Northwestern Polytechnical University.He received the Ph.D.degreefrom the same university in 1993.His major research interests are vibration and control design of aircraft structure.
14 September 2015;revised 5 December 2015;accepted 10 February 2016
Available online 27 August 2016
Aeroelasticity;
Flutter;
Integral boundary-layer;
Transonic flow;
Unsteady flow
©2016 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.Tel.:+86 29 88495451.
E-mail address:heerming@nwpu.edu.cn(E.He).
Peer review under responsibility of Editorial Committee of CJA.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Flapping wing micro-aerial-vehicle:Kinematics,membranes,and flapping mechanisms of ornithopter and insect flight
- A new non-linear vortex lattice method:Applications to wing aerodynamic optimizations
- Experimental study of flow field distribution over a generic cranked double delta wing
- Streamwise-body-force-model for rapid simulation combining internal and external flow fields
- An artificial neural network approach for aerodynamic performance retention in airframe noise reduction design of a 3D swept wing model
- effects of wing locations on wing rock induced by forebody vortices
