随机产汇流理论

芮孝芳

（河海大学水文水资源学院，江苏南京 210098）

随机产汇流理论

芮孝芳

（河海大学水文水资源学院，江苏南京 210098）

引入随机理论，将流域上一场具有一定时空分布的降雨视作无穷多雨滴之集合。流域上任一位置雨水的下渗、蒸散发，以及向流域出口断面的汇集，用水动力学处理；呈时空分布的无穷多雨滴的集体表现，即流域产流量的形成和流域出口断面流量的形成，则用概率论处理。从而同时考虑了降雨空间分布不均和下垫面条件空间变异对流域产流的影响，也揭示了流域瞬时单位线的物理本质，阐明了倍比性和叠加性是净雨空间分布均匀条件下流域汇流的本质特性。最后提出了一个确定流域汇流速度空间分布的方法。

流域产汇流；随机理论；雨滴；蓄满产流；超渗产流；流域瞬时单位线；流域汇流速度

产汇流理论探讨的科学问题是流域降雨径流形成的机理和规律，是水文学核心内容之一［1］。从产汇流理论百年发展历程可以看出，牛顿力学起着重要的作用。基于牛顿力学，水文学家已较好地揭示了流域上任一点降雨产流的物理条件，以及净雨水滴向流域出口断面运动汇集的机理。但流域产流是时空分布不均的降雨作用于空间变异性的包气带的“集体”表现；流域汇流是分布在流域上无穷多个净雨水滴向流域出口断面运动的“集体”表现。人们通过观测得到的一场降雨形成的流域出口断面流量过程则是这些净雨水滴“集体”表现的结果。对于这些“集体”表现机理的揭示，牛顿力学显得“力不从心”，因为这里涉及如何处理微观与宏观的关系问题。在热力学的发展过程中最先遇到这样的问题。统计物理学就是为着处理这样的问题发展起来的学科［2］。它用随机理论成功地揭示了微观的气体分子运动与宏观的气体体积、压强和温度之间的关系。受统计物理学的启发，笔者试图引入随机理论来揭示“点”产流与流域产流、“水滴”汇流与流域汇流等微观与宏观的关系，故本文定名为“随机产汇流理论”。

1　“点”产流的物理机理

产流量是降雨量扣除降雨期间损失量的余额。降雨期间的损失量包括三部分［3］：一是植物截留和填洼量；二是雨期蒸散发量；三是被土壤保持的下渗水量。雨期蒸散发量取决于蒸散发规律；被土壤保持的下渗水量取决于下渗规律；植物截留量和填洼量最终也耗于蒸散发或下渗。因此，产流问题本质上就是蒸散发和下渗问题。

西方文献记载，早在公元前1世纪就有“降落在山地区域的雨水和雪水渗透到地表以下，然后在低洼地出露，形成河流和泉”的说法［4］。中国在公元8世纪也有“坟垆燥疏，渗渴而升。充融有余，泄漏复行”的描述［5］。后者已与“蓄满产流”的概念很接近了。现代产流理论始于20世纪30年代，近百年来，经过Horton［6］、Linsley等［7］、Kirkby［8］、赵人俊［9］等学者的理论或试验研究，已得出基质土壤包气带产流的物理条件：一是下渗水量使包气带缺水量得以满足，得到的产流量包括多种径流成分；二是降雨强度超过地面下渗能力，得到的产流量只包括超渗地面径流；三是包气带中存在一个或多个相对不透水层，这既是产生壤中水径流的条件，也是产生饱和地面径流的条件。

由此，可以归纳成两种基本产流模式［3］：其一为蓄满产流模式，特点是降雨量扣除雨期蒸散发，通过下渗，满足包气带缺水量后尚有剩余，其产流量由所形成的不同径流成分组成；其二为超渗产流模式，特点是包气带缺水量虽未得到满足，但降雨强度扣除蒸散发强度超过了地面下渗能力，其产流量仅为超渗地面径流一种径流成分。

令X为点降雨量，I为点降雨强度，E为点雨期蒸散发量，J为点雨期蒸散发强度，Wm为点包气带田间持水量，W0为降雨开始时刻点包气带含水量，Wm与W0之差称为点包气带缺水量，用D表示，即D=Wm-W0，K为点地面下渗能力，Y为点产流量，R为点产流强度，则可得蓄满产流模式的产流判别式为

点产流量

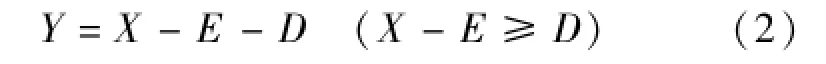
超渗产流模式的产流判别式为

点产流强度

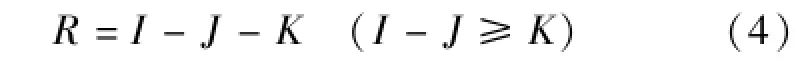
若定义X′=X-E，I′=I-J，则式（1）和式（2）分别变为

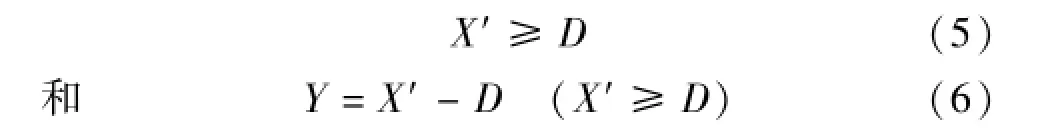
而式（3）和式（4）分别变为

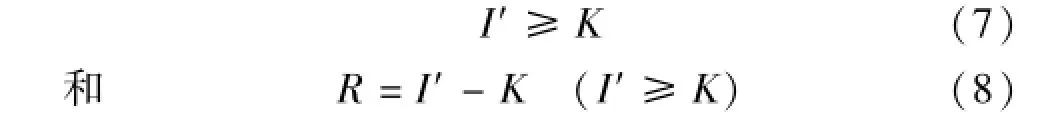
式（6）和式（8）分别是蓄满产流模式和超渗产流模式计算点产流量或点产流强度的数学表达式。流域上任一点，只要属于蓄满产流模式，就可用式（6）定量；只要属于超渗产流模式，就可用式（8）定量。

2　空间分布的概率释义

大气中积雨云携带着数量大到趋于无穷的水滴，其中凡能以液态水形式降落到地面的就成为雨滴。降雨过程中，某时段或某时刻在流域不同位置均可对降雨量或降雨强度进行观测。显然，降雨量或降雨强度存在空间分布。若测得的流域上每个位置的降雨量或降雨强度相同，则降雨空间分布是均匀的，否则是不均匀的。如果已经取得了降雨量或降雨强度空间分布的密集大数据，那么就可按下列方法来精细刻画其空间分布：给定降雨量或降雨强度的数值0，x1，x2，…，xi-1，xi，…，xn（xi＞xi-1，i=1，2，…，n），令xi-xi-1=Δx，统计每一个数值间隔所占的面积ai。以xi为横坐标，ai为纵坐标，可作出如图1（a）所示的柱状图；以x为横坐标，以小于或等于该x所占的面积∑a为纵坐标又可作出图1（b）所示的不及制累积曲线。

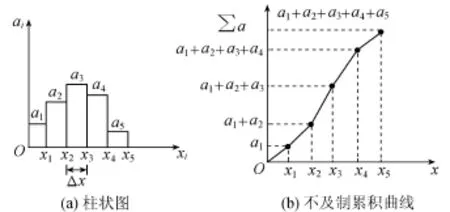
图1　降雨空间分布

积雨云携带的雨滴降落在流域某处是随机的，即在某时段或某时刻以多少数量雨滴降落在流域上某位置是随机的，或者说，流域上某一位置在某时段或某时刻会降落多少雨滴是随机的。因此，若用随机性思维解释降雨现象，降雨量或降雨强度就是一个随机变量，其所占据的面积与全流域面积之比即为它在流域上出现的概率。基于这种思维，图1就与随机变量降雨量或降雨强度的概率分布有关了，因为若将图1（a）的纵坐标改为pi=ai/A（i=1，2，…，n），其中A为流域面积，它就成为降雨量或降雨强度的概率分布了（图2（a））。再将图2（a）之纵坐标改为pi/Δx并取Δx→0的极限，它就进一步成为降雨量或降雨强度的概率密度f（x）了（图2（b））。而对图2（b）所示的概率密度f（x）求事件｛X≤x｝的概率P｛X≤x｝，就可得不及制分布函数F（x）（图2（c））：

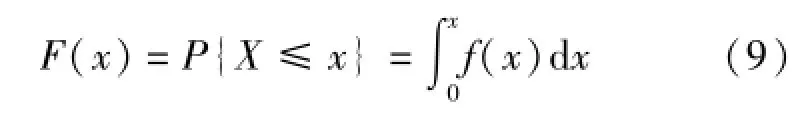
同理，可对包气带缺水量的空间分布和地面下渗能力的空间分布作出概率释义。根据包气带缺水量和地面下渗能力空间分布的密集大数据就可分别求得它们的概率密度和分布函数。包气带缺水量的概率密度为f（d），分布函数为F（d）；地面下渗能力的概率密度为f（fp），分布函数为F（fp）：

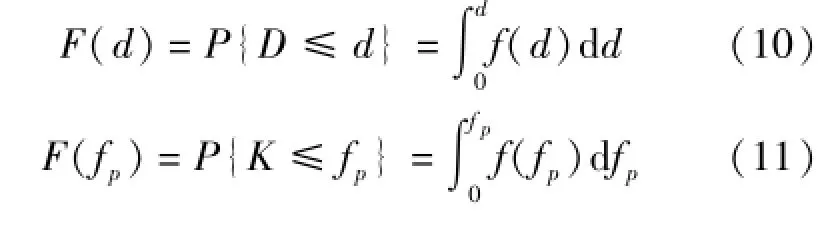
3　流域产流的随机方法

对于蓄满产流模式，其产流的物理条件和点产流量的表达式分别为式（5）和式（6）。因为X′和D均可视作为随机变量，因此，作为这两个随机变量的函数Y也必是随机变量，而且从物理概念得知，事件｛X′≥D｝的概率P｛X′≥D｝是流域中产流面积占全流域面积的比例；事件｛Y≤y｝的概率P｛Y≤y｝是蓄满产流模式下点产流量Y的分布函数F（y），也就是以不及制累积曲线表达的产流量在流域上的空间分布。根据随机变量函数的分布函数理论［10］，由式（5）可导得概率P｛X′≥D｝：

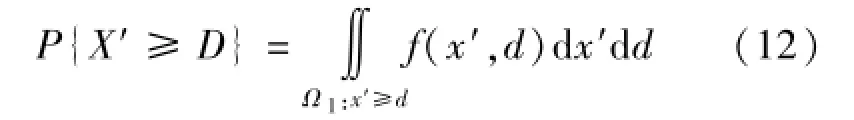
由式（6）可导得概率P｛Y≤y｝的空间分布：

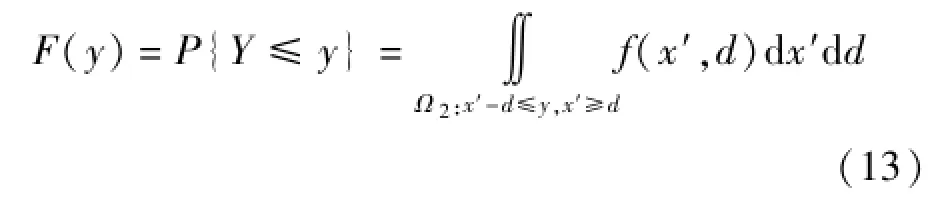
式（12）和式（13）中之f（x′，d）为随机变量X′和D的联合概率密度；Ω1、Ω2为积分域，见图3和图4。

由于一般情况下没有充分理由认为随机变量X′与D之间存在联系，因此可认为它们是两个相互独立的随机变量，这样就有f（x′，d）=fx′（x′）· fd（d），将其代入式（12）和式（13）可便于积分计算。

根据式（13）可求得以水深表示的由净雨水滴组成的流域产流量为

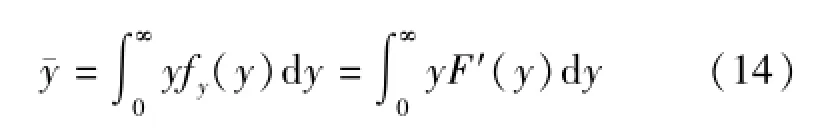
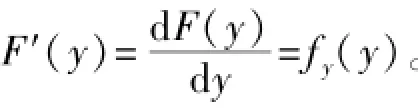
因此，对于蓄满产流模式，只要获得降雨量的空间分布，又掌握了包气带缺水量的空间分布，就可以利用式（12）求出产流面积所占比例，利用式（14）求出以水深表示的流域产流量。

对于超渗产流模式，可按相同方法求得其产流面积所占比例和以水深表示的流域产流量。

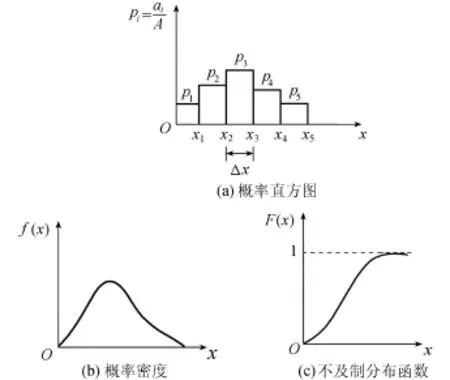
图2　视作概率密度和分布函数的降雨空间分布

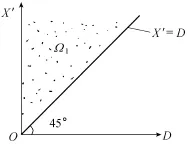
图3　积分域Ω1

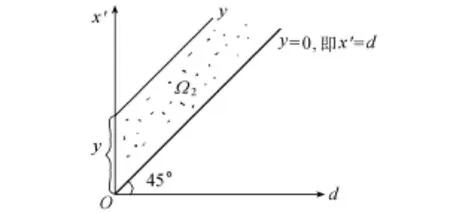
图4　积分域Ω2

4　观察汇流的新视角

组成流域产流量的净雨水滴向流域出口断面汇集就形成了流域出口断面流量过程。由于这些净雨水滴是通过不同介质、不同路径、不同粗糙面向流域出口断面运动的，因此流域汇流十分复杂，以致形成了多视角揭示其机理、探索其规律的局面。100多年来，经过St.Vennat、Sherman、McCarthy、加里宁、米留柯夫、Nash、Rodriguez-Iturbe等学者的研究和探索，观察和分析流域汇流的视角可以归纳为4种［1，3，11］：一是水动力学视角，认为流域汇流是连续介质的水流运动，因而可用连续性方程和动力方程来探讨其规律；二是水文学视角，认为流域出口断面流量过程是净雨过程在流域调蓄作用下演化出来的，因而可用水量平衡方程和蓄量方程来探讨其规律；三是水滴运动学视角，认为一定时空分布的净雨是由大量水滴组成，每个水滴运动到流域出口断面都要经历一定的汇流时间，汇流时间相同的水滴就组成了同一时刻的流域出口断面的流量，这样就导出了径流成因公式，并产生了等流时线概念；四是系统论视角，认为流域汇流是一个系统问题，净雨过程是其输入，流域出口断面流量过程是其输出，流域下垫面的作用就是系统作用。流域出口断面流量过程是净雨过程受系统作用而形成，若假设流域汇流系统属于线性时不变系统，则可利用倍比性和叠加性来进行流域汇流计算，从而产生了单位线概念。

尽管已经有4种视角揭示流域汇流机理、探索流域汇流规律，但仍存在一些令人感到困扰的问题。例如：如何清楚阐明流域汇流速度的物理概念；如何确定流域汇流速度；倍比性和叠加性是不是一种假设；如果流域汇流具有非线性，那么导致这种非线性的内在原因是什么；等等。因此寻找新的视角仍有必要。

降落在流域不同位置的净雨水滴在向流域出口断面汇集的过程中，不仅历经的路径不同，路径的几何长度各异，而且沿路径的坡度、糙率等也存在差别，这就导致处在流域不同位置上的净雨水滴必然要花费不同的汇流时间才能到达流域出口断面，汇流时间短的净雨水滴先到达，汇流时间长的水滴后到达。令净雨水滴落地时间为T′，落地至到达流域出口断面的汇流时间为T"，落地至出现在流域出口断面的时间为T，则必有

流域上均匀分布的每个净雨水滴都可以写出式（15），这样将可写出无穷多个式子。这无穷多个表达式表达了每个净雨水滴的流域汇流过程，其“集体”表现形成了流域出口断面流量过程。着眼于一个个水滴的汇集是微观思考，着眼于它们的“集体”表现是宏观思考。笔者将这种从微观与宏观的关系上观察流域汇流的视角称为“统计物理视角”。本文讨论流域汇流采用的就是这个新视角。

5　时间过程的概率释义

对流域上任一位置而言，净雨水滴将在什么时间落地，显然具有随机性。因此，净雨水滴落地时间T′可视作随机变量。用这种思维来考察流域上任一位置的净雨过程线，可以证明将它归一化后就是T′作为随机变量的概率密度［12］。事实上，若将降雨历时按Δt划分成若干个时段（图5（a）），则时段净雨量对这场净雨总量之比就是净雨水滴在这个时段内落地的概率（图5（b）），再将这个概率除以Δt，并令Δt→0，就可最终得到净雨水滴落地时间的概率密度fh（t）（图5（c））：式中h（t）为净雨空间分布均匀时流域上任一位置的净雨过程。

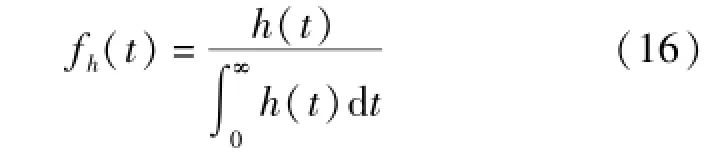
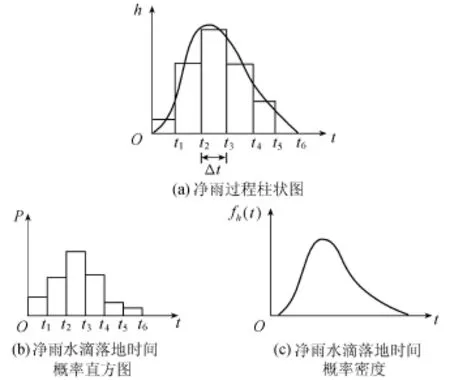
图5　视作概率密度的时间过程

同理，可将流域出口断面流量过程解释为净雨水滴到达流域出口断面的时间这一随机变量的概率密度，记作fQ（t）。

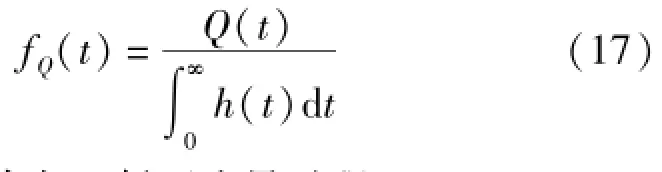
式中Q（t）为流域出口断面流量过程。

6　流域瞬时单位线的物理意义

上述关于净雨过程和流域出口断面流量过程的概率释义表明，式（15）中的T′和T均为随机变量，那么T′与T之和T"也必定是随机变量。而且从流域汇流的物理成因上可以推测随机变量T′和T"是相互独立的。因此，由概率论中独立随机变量和的分布函数理论可知，式（15）中3个随机变量的概率密度服从下列卷积分关系［10］：

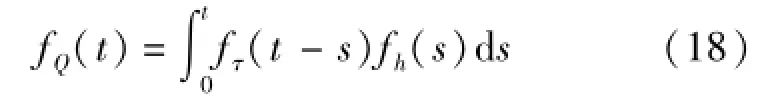
式中：fτ（t）为净雨水滴流域汇流时间的概率密度；其余符号的意义同前述。

将式（16）和式（17）代入式（18），并考虑水量平衡有［12］

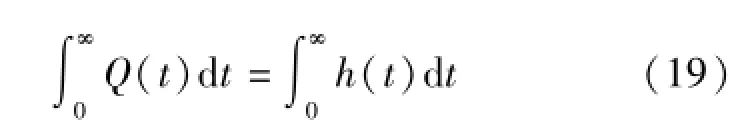
式（18）则化为

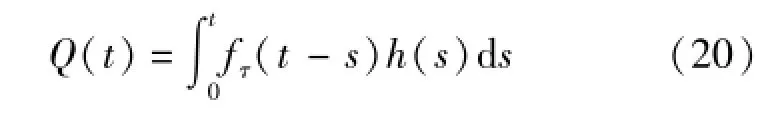
式（19）和式（20）成立的条件是净雨空间分布均匀。

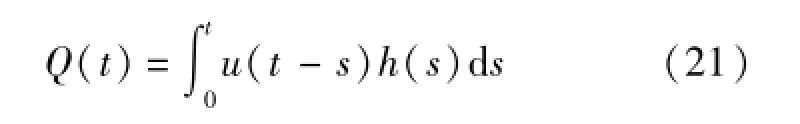
在系统论视角下，当汇流系统为线性时不变系统时，必有式中：u（t）为流域瞬时单位线（IUH），在系统论视角下它定义为空间分布均匀、历时趋于零、强度趋于无穷大，但总量为1个单位的净雨形成的流域出口断面流量过程。

比较式（21）和式（20）不难发现

式（22）就是流域IUH的概率释义。最早发现这一结论的是Rodriguez-Iturbe等，时间为1979年。

从以上推导中，笔者得出了下列几点认识：

a.流域汇流之所以服从倍比原理和叠加原理，也就是流域汇流系统是线性时不变系统，是因为T′和T"相互独立。只要净雨空间分布均匀，就可以按卷积分公式进行流域汇流计算。

b.流域IUH的物理实质是均匀分布在流域上的净雨水滴汇流时间的概率密度，因为若净雨空间分布不均匀，则式（19）就不能成立，从而就无法得到式（20）。

c.流域汇流非线性的物理原因主要是净雨水滴空间分布不均匀。

7　流域汇流速度的空间分布

水文学发展到今天，还没有产生直接测定净雨水滴流域汇流速度的方法，更无法直接给出它的空间分布。笔者认为利用本文提出的考察流域汇流的新视角可以实现给出流域汇流速度空间分布的梦想。

事实上，流域上任一位置处的净雨水滴的汇流速度可由下式确定：

式中：V为净雨水滴的汇流速度；L为净雨水滴汇流路径的长度。

由于净雨水滴何时落地，何时汇集到流域出口断面均是随机的，因此式（23）中之L和T"均为随机变量，以致V也必为随机变量。根据概率论中随机变量函数的分布理论，只要已知L和T"的概率分布，就可求得V的概率分布［10］：

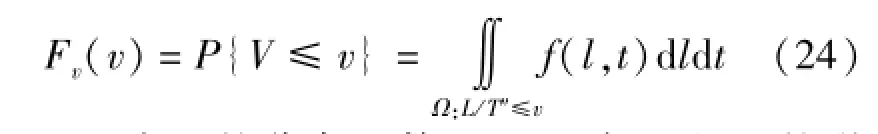
式中：Fv（v）为V的分布函数；f（l，t）为L和T"的联合概率密度；Ω为积分域（图6）。

从物理上可以判断，L和T"是相互独立的，于是式（24）可化简成：

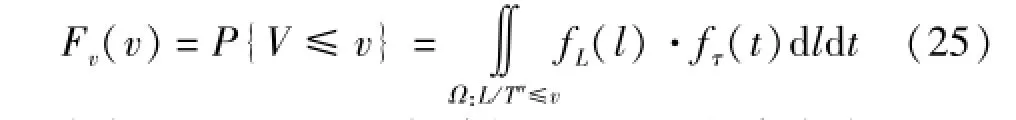
式中fL（l）和fτ（t）分别为L和T"的概率密度。fτ（t）可由实测降雨径流资料求得；fL（l）可借助于DEM求得［13］，也可用宽度函数或时间面积曲线替代［14-15］。

式（25）即为求得的净雨水滴汇流速度以不及制累积曲线表示的空间分布。据此，还可进一步求得平均流域汇流速度为

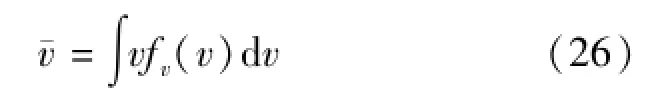
其中

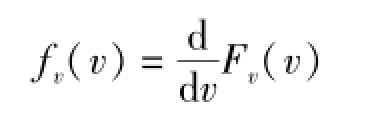
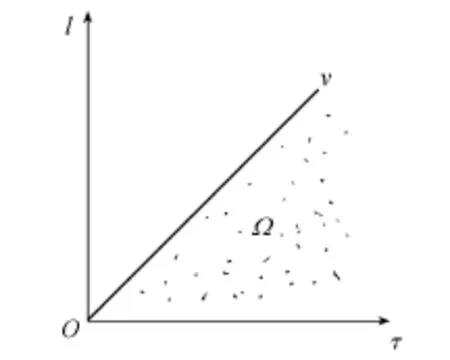
图6　积分域Ω

8　结 语

将水动力学作为产汇流理论基础的观点已有很长的时间了，但这种观点遇到了一些困难，例如难以处理降雨和下垫面条件空间分布都不均匀导致的“产流场”时空变化对产汇流的影响；难以清晰揭示其中水流或净雨水滴向流域出口断面汇集的机理和流域汇流时间的物理本质等。

受统计物理学思想的启发，笔者相信许多自然现象的机理和规律应通过宏观和微观两种相互补充的思维才能得以揭示。对于产汇流现象，单个雨滴在流域中的运动遵循牛顿力学定律，属于水动力学问题，但分布在流域中无穷多雨滴运动的“集体”表现，牛顿力学就显得“力不从心”，而需要依靠概率论来揭示。因此，要解决产汇流理论中遇到的困难，需依靠牛顿力学与概率论的结合和互补，才能找到解决困难的理论和方法。

事实上，人们观测到的降雨量、降雨强度、包气带缺水量、地面下渗能力、流域出口断面流量等的时空变化，都是一些随机变量的概率密度。降雨量、降雨强度、包气带缺水量、地面下渗能力等的空间分布是作为随机变量的降雨量、降雨强度、包气带缺水量、地面下渗能力等的概率密度；而降雨量时间过程、降雨强度时间过程、流域出口断面流量时间过程等则是作为随机变量的降雨量、降雨强度、流域出口断面流量等出现时间的概率密度。

基于上述认识，笔者得出：流域产流计算是一个推求两个随机变量之差的分布函数问题；流域汇流计算是一个推求两个随机变量之和的分布函数问题；当净雨空间分布均匀，且净雨水滴落地时间与其到达流域出口断面时间不存在相互影响时，倍比性和叠加性不是一个假设而是一种机理；流域IUH的物理本质是均匀分布在流域上的净雨水滴汇流时间的概率密度，它只适用于净雨空间分布均匀的情况。

［1］芮孝芳.产汇流理论［M］.北京：水利电力出版社，1995.

［2］陈仁烈.统计物理引论［M］.北京：人民教育出版社，1959.

［3］芮孝芳.水文学原理［M］.北京：高等教育出版社，2013.

［4］BISWAS A K.水文学史［M］.刘国纬，译.北京：科学出版社，2007.

［5］芮孝芳.中国地学通鉴·水文卷［M］.西安：陕西师范大学出版社，2016.

［6］HORTON R E.Surface runoff phenomena［R］.Ann Arbor：Horton Hydrology Laboratory Publication，1935.

［7］LINSLEY R K，KOHLER M A，PAULHUS J L H. Hydrology for Engineers［M］.3rd ed.New York：McGraw-Hill，1988.

［8］KIRKBY M J.Hillslope hydrology［M］.New York：John Wiley&Sons，1974.

［9］赵人俊.流域水文模拟［M］.北京：水利电力出版社，1984.

［10］复旦大学数学系.概率论与数理统计［M］.上海：上海科学技术出版社，1960.

［11］RODRIGUEZ-ITURBE I，VALDES J B.The geomorphological structure of hydrologic response［J］.Water Resources Research，1979，15（5）：1409-1420

［12］芮孝芳.流域汇流的概率论体系探讨［J］.水科学进展，2004，15（2）：135-139.（RUIXiaofang.Studyof mechanism of watershed concentration flow based on probability theory［J］.Advances in Water Science，2004，15（2）：135-139.（in Chinese））

［13］宫兴龙.流域地貌特征及流域地貌单位线研究［D］.南京：河海大学，2009.

［14］芮孝芳.由流路长度分布律和坡度分布律确定地貌单位线［J］.水科学进展，2003，14（5）：602-606（RUI Xiaofang.Studyofdetermininggeomorphologicunit hydrograph by means of probability density function of path length［J］.Advances in Water Science，2003，14（5）：602-606（in Chinese））

［15］芮孝芳.水文学前沿科学问题之见［J］.水利水电科技进展，2015，35（5）：95-102.（RUI Xiaofang.Discussion of some frontier problems in hydrology［J］.Advances in Science and Technology of Water Resources，2015，35（5）：95-102.（in Chinese））

Random theory of runoff yield and flow concentration

Rui Xiaofang
（College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China）

Rainfall with time and space distribution is regarded as muster of infinitely great“drop of rainfall”from the view of random theory.Infiltration，evapotranspiration and flow concentration for rainfall of a point located in the watershed can be handled by hydrodynamics.The collective expression of infinitely great“drop of rainfall”with space distribution，i.e.，formations of runoff yield and flow concentration of watershed can be handled by probability theory.The above-mentioned idea not only resolves the runoff yield of watershed affected by space variations of rainfall and underlying surface condition，but also reveals physical nature of watershed instantaneous unit hydrograph（IUH），i.e.，proportionality and superposition of watershed flow concentration.Finally，a method for determining space distribution of flow concentration velocity is put forward.

runoff yield and flow concentration of watershed；random theory；drop of rainfall；runoff formation at natural storage；runoff formation in excess of infiltration；instantaneous unit hydrograph of watershed；watershed flow concentration velocity

P333.2

A

10067647（2016）05000805

10.3880/j.issn.10067647.2016.05.002

国家自然科学重点基金（41430855）

芮孝芳（1939—），男，教授，主要从事水文学及水资源研究。E-mail：jiangguol@hotmail.com

（20160517 编辑：骆超）