车辆多轮随机动载作用下柔性沥青路面的应变分析

陈 洋， 戴宗宏， 陈焕明， 刘大维

(青岛大学 机电工程学院，山东 青岛 266071)



车辆多轮随机动载作用下柔性沥青路面的应变分析

陈 洋， 戴宗宏， 陈焕明， 刘大维

(青岛大学 机电工程学院，山东 青岛 266071)

为进行车辆多轮随机动载作用下柔性沥青路面的应变分析，采用有限元分析软件ABAQUS建立考虑柔性沥青路面黏弹性的三维有限元模型，仿真计算车辆多轮随机动载作用下柔性沥青路面三个方向的应变响应，分析车辆多轴作用下路面应变时程变化特性，得到路面各点的最大应变。结果表明， 在路面某一位置，三种沥青材料组成的沥青各层顶面和下面层底面产生的三个方向的应变大小及变化规律均不相同；沥青上面层顶面和下面层底面无论是路面长度方向还是宽度方向，各点的三个方向的最大应变均不相同，沿路面长度方向，中、后轴车轮荷载产生的应变大于前轴车轮荷载产生的应变，且横向应变大于纵向和垂向应变。研究结果可为柔性沥青路面结构设计与路面寿命分析及预测提供参考依据。

随机动载；柔性沥青路面；黏弹性；应变；有限元

随着我国高等级公路建设的不断发展，交通量迅速增长，车辆大型化、车辆超载、车辆渠化行驶等问题日趋严重。沥青路面常出现龟裂、横向裂缝、纵向裂缝、开裂、坑槽、车辙等破坏现象，严重降低了道路使用性能。在设计路面结构、分析路面性能和进行路面疲劳寿命分析时，必须了解车辆荷载作用下路面的应变变化，最大应变值的产生位置等，才能确保路面的使用寿命。多年来，线弹性层状理论作为经典的分析方法被大量学者应用于路面分析。但对柔性沥青路面而言，沥青混合料的黏弹性特性与车辆轮轴数、轮胎动荷载、作用时间等有关，线弹性分析模型计算车辆荷载作用下路面结构中应力和应变，已无法精确地进行路面力学行为的定性和定量的描述[1-2]。为了更加准确的模拟、预测车辆引起的路面动态响应，许多学者考虑了柔性沥青路面结构的黏弹性和非线性[3-9]。目前在研究车辆动载作用下路面动态响应特性方面，大多对车辆荷载进行了简化[10-15]，难以全面分析车辆多轮荷载对柔性沥青路面性能的影响。基于此，本文建立多轴车辆多轮随机动载作用下考虑柔性沥青路面黏弹性的三维有限元模型，分析多轴车辆多轮随机动载作用下柔性沥青路面应变的动态变化特性，为柔性沥青路面结构设计与路面寿命分析及预测提供参考依据。

1 车辆动载作用下路面结构动力学有限元方程

根据弹性动力学理论，车辆多轮动载作用下路面多层结构动力学有限元方程为：

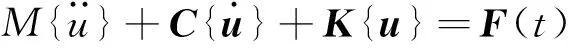
(1)

式中：M为路面系统质量矩阵；C为路面系统阻尼矩阵；K为路面系统刚度矩阵；u为节点位移向量；F(t)为车辆多轮动载荷矩阵。

路面系统阻尼矩阵采用瑞利阻尼假设求解：

{C}=α{M}+β{K}

(2)

式中：α和β是与路面结构材料、固有频率和阻尼比有关的比例常数[16]。

2 柔性沥青路面结构有限元模型

柔性沥青路面结构如图1所示，由沥青上面层(改性沥青SMA13)、中面层(改性沥青Sup20)、下面层(普通沥青Sup25)、基层(级配碎石)和土基组成。

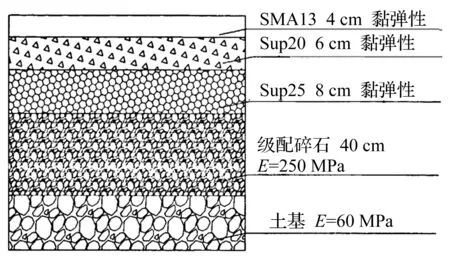
图1 沥青路面结构Fig.1 The structure of the asphalt pavement

在建立柔性沥青路面三维有限元模型时，选取路面长为100 m，宽为18 m，高为5 m，采用ABAQUS有限元软件中的C3D8R六面体单元对路面结构进行网格划分。考虑到计算效率和计算精度，在宽度方向将车辆车轮接触区域网格细化，网格尺寸为0.015 m～0.085 m，车辆车轮非接触区域网格尺寸为0.6 m；在长度方向(车辆前进方向)网格尺寸均为0.2 m；在深度方向，沥青上面层、中面层、下面层分别划分为2层、3层、4层，基层和土基划分为4层和15层。所建立的路面结构各层之间的接触面为完全连续，整个路面结构单元数目为588 000个，节点数目为624 747个，沥青路面结构有限元模型如图2所示。

柔性沥青路面结构模型各层参数如表1所示[17]。

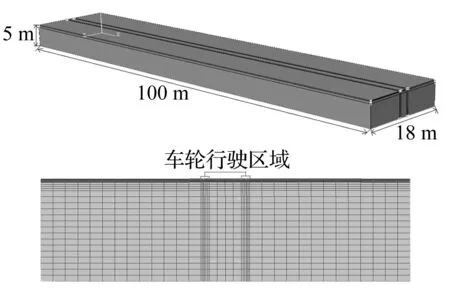
图2 沥青路面结构有限元模型Fig.2 The finite element model of the asphalt pavement

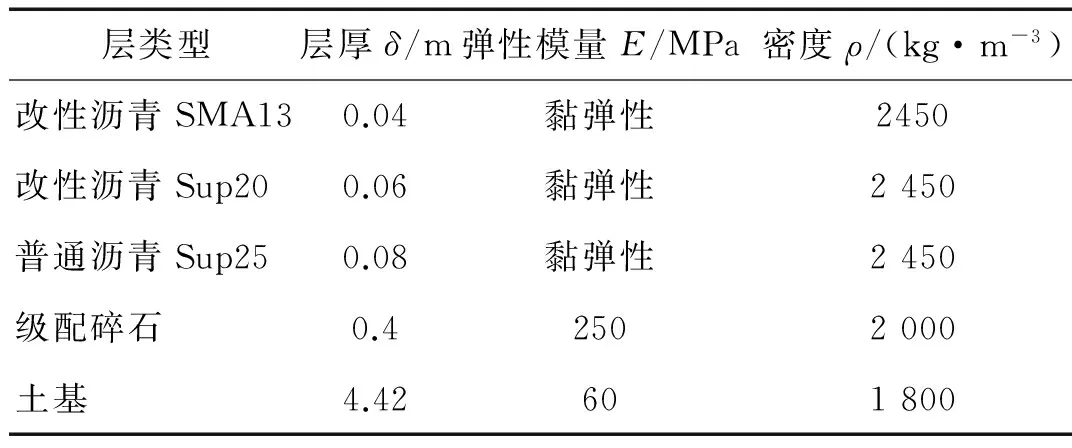
层类型层厚δ/m弹性模量E/MPa密度ρ/(kg·m-3)改性沥青SMA130.04黏弹性2450改性沥青Sup200.06黏弹性2450普通沥青Sup250.08黏弹性2450级配碎石0.42502000土基4.42601800

对于沥青层的黏弹性属性，可根据沥青混合料不同温度和荷载频率下复数模量实验结果，通过基本黏弹性关系转化确定其松弛模量，在ABAQUS中用Prony级数系列来表征。各沥青混合料Prony系列的系数(25℃)如表2所示[17]。

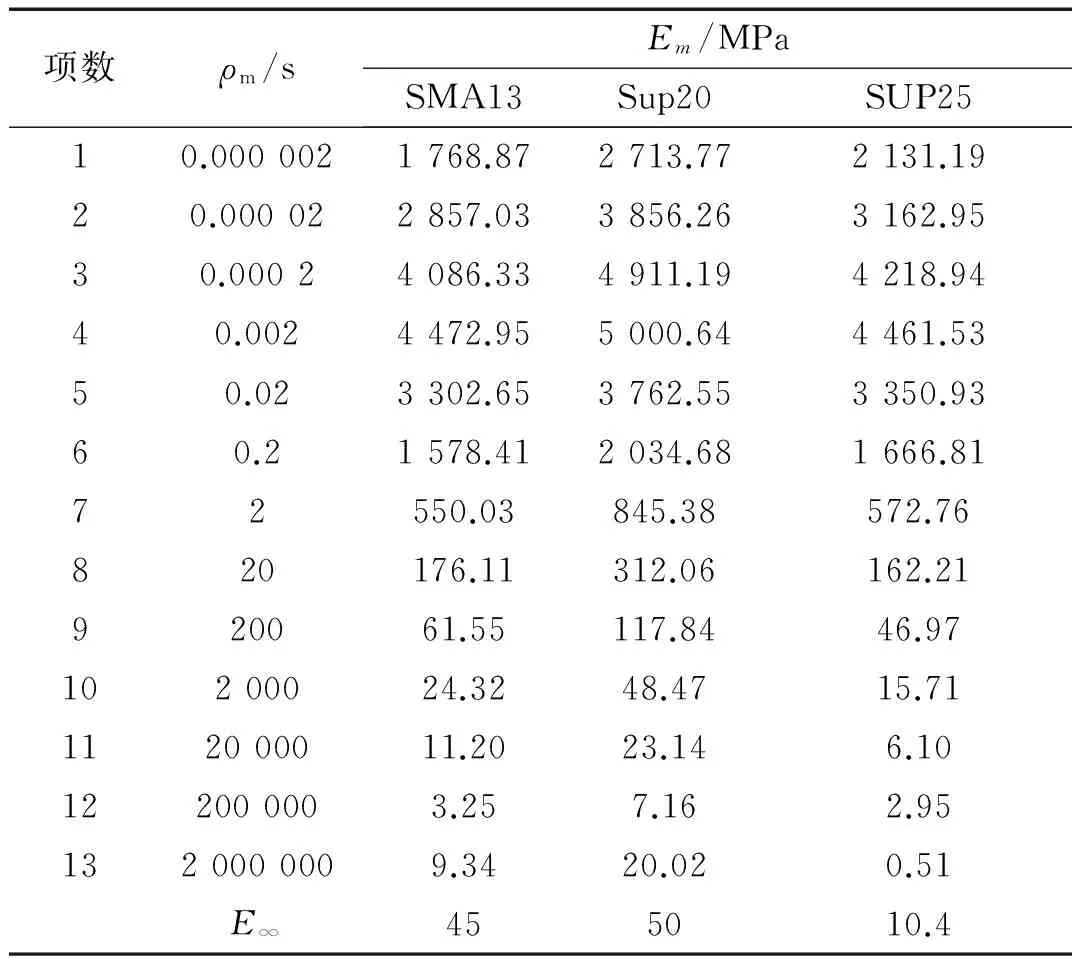
表2 松弛模量Prony系列系数/MPa

3 车辆多轮动载荷及加载

随机动载是车辆在不平路面上行驶时，因路面不平度而引起车辆振动产生的。随机动载用与路面相互作用的车辆轮胎动载荷来描述，可利用质量-弹簧-阻尼单元组成的车辆振动模型，或利用多体动力学方法建立整车行驶动力学模型，仿真计算轮胎动载荷。为较为准确地获得多轴车辆多轮轮胎动载荷，本文采用基于路面有理函数功率谱密度的谐波叠加法建立双轮辙空间域B级路面不平度模型，并采用多体动力学仿真软件SIMPACK建立刚柔耦合的整车行驶动力学模型(图3)，计算车辆各轴轮胎动载荷[18-19]。

车辆为某重型自卸汽车，满载质量27 000 kg，前轴载荷70 kN，中、后轴载荷各为100 kN，前轴和中轴距为3.865 m，中轴和后轴距为1.36 m，前轴轮距为2.02 m，中、后轴轮距为1.84 m，轮胎压力为0.95 MPa。

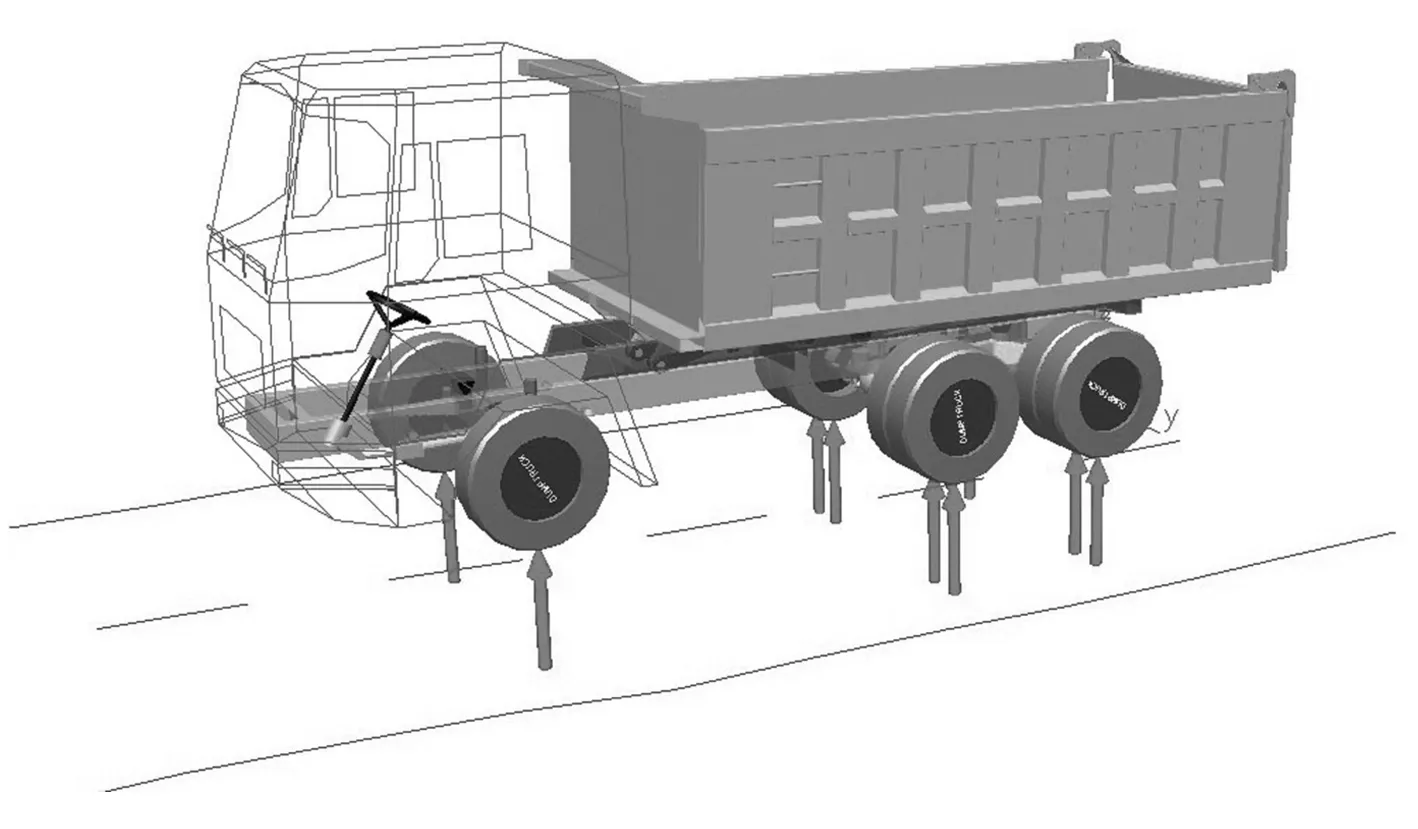
图3 整车行驶动力学模型Fig.3 Dynamic multi-body model of heavy vehicle

图4为车辆满载，车速为60 km/h时，前轴、中轴、后轴两侧轮胎的法向作用力随行驶距离的变化曲线。

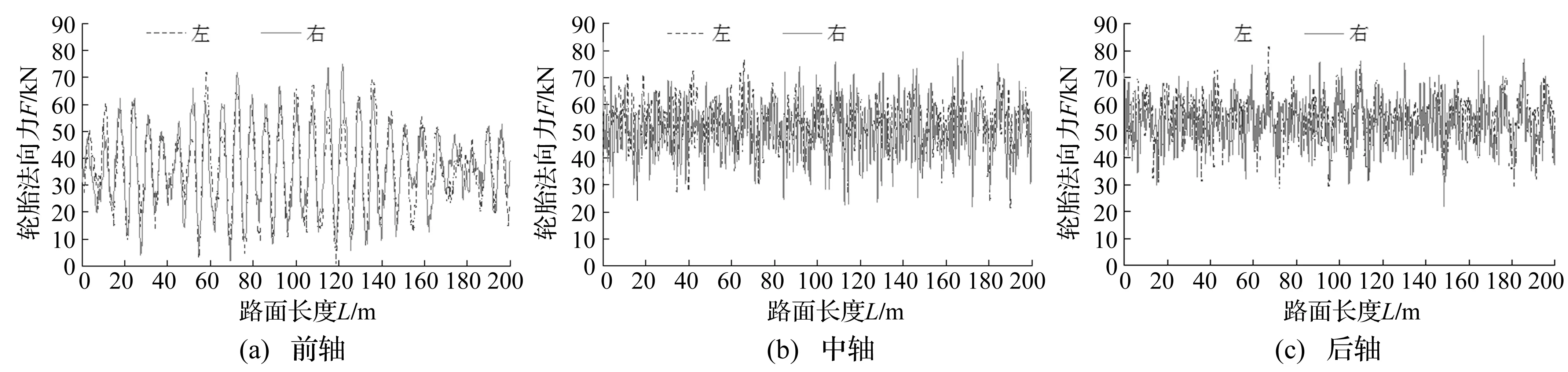
图4 车辆各轴轮胎法向力Fig.4 The normal force of the vehicle wheels

为了模拟车辆行驶过程中车辆各轴车轮动载的作用效果，在ABAQUS软件中用子程序vdload施加移动载荷。vdload子程序可以用来定义一组关于位置时间和速度的函数，能很好地模拟垂直压力在路面上的移动加载过程。当车速为60 km/h时，求解的轮胎法向作用力频率为170.5 Hz，时间间隔为0.005 8 s，也就是每一次取得的载荷在这个时间间隔内按不变处理，在下一个时间间隔内取另一组数值。由于vdload子程序对加载区域施加的是面载荷，因此需对各个车轮法向载荷进行处理，得到相应面载荷数值，再将其加载到沥青路面有限元模型上。对于车辆各轴车轮如此众多的载荷数据直接编写子程序十分困难，本文利用Python脚本语言编写程序，将获得的车轮载荷数据填充到vdload子程序。

试验表明，重型车辆接地印迹近似为矩形[20]，本文所用车辆前、后轮胎与路面的接触印迹分别为0.158 m×0.229 m和0.194 m×0.272 m的矩形，接地面积分别为0.036 1 m2和0.052 6 m2[21]。

4 仿真结果及分析

图5为车辆左侧车轮随机动载作用下路面某一位置的沥青层三个方向应变时程变化曲线。

由图5可知，三轴车辆通过路面时，当车轮接近与离开该位置时，三个方向的应变均发生了较大变化，三种沥青材料组成的沥青各层顶面和下面层底面产生的三个方向的应变大小及变化规律均不相同，三个层顶面的三个方向应变变化规律基本相似，垂向应变为拉应变，纵向应变出现拉压应变变化，横向应变为压应变，且横向压应变最大；沥青下面层底面(Sup25)应变变化与各层顶面的应变变化不同，垂向应变为压应变，纵向应变出现压拉应变变化、横向应变为拉应变，且横向拉应变最大。由此可见，沥青路面的破坏一方面是由于沥青上面层受到较大的压应变而产生的自上而下的破坏；另一方面，由于沥青下面层底面受拉应变作用，将会向上拱起，使得沥青下面层底面与粒料基层发生分离，产生一种自下而上的破坏。

从垂向应变的时程变化来看(见图5(a))，沥青顶面各层在车轮荷载作用过程中均呈现拉应变状态，且随着车辆前轮接近该位置，沥青各层顶面的垂向拉应变逐渐变大；当车轮作用在该位置时，垂向拉应变变小；在车辆后轮离开后，需要较长时间才能恢复到初始状态；而沥青下面层底面(Sup25)始终处于压应变状态，且变化趋势与沥青各层顶面正好相反。

从纵向应变的时程变化来看(见图5(b))，当车辆前轮和中轮接近该位置时，沥青各层顶面纵向应变为拉应变；当车轮作用在该位置时，纵向应变变为压应变；当车辆前轮离开该位置时，纵向应变变为拉应变；当中轮离开时，由于中、后轴轴距较小，纵向压应变虽有所减小，但随着后轮荷载的再次作用，纵向压应变再次增大；当后轮离开该位置时，纵向应变又变为拉应变；而沥青下面层底面(Sup25)的纵向应变变化趋势与沥青各层顶面正好相反。上述现象也说明柔性沥青路面材料具有典型的黏弹性特性。

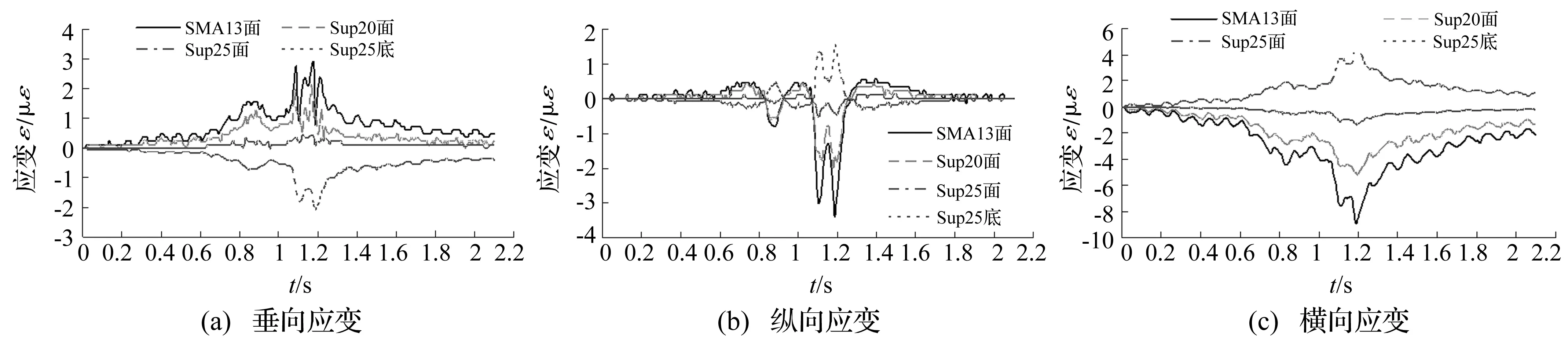
图5 沥青层应变时程变化曲线Fig.5 The strain time history curves of the asphalt layers

从纵向应变的时程变化可以看出，在车辆驶过的整个过程中，沥青层经历了拉-压-拉应变的交变变化，在实际沥青路面结构中，车辆随机荷载的反复作用会使路面出现反复的拉压交变作用，而这种长期的交变作用必然会导致沥青路面疲劳破坏的产生。

从横向应变的时程变化来看(见图5(c))，沥青各层顶面在车轮荷载作用的过程中均呈现压应变状态，而沥青下面层底面(Sup25)始终处于拉应变状态。

图6为车辆前轴和中、后轴左侧车轮通过路面时，沿路面长度方向沥青上面层顶面(SMA13)和下面层底面(Sup25)最大应变变化曲线。

由图6可看出，在路面长度方向的不同位置，路面三个方向最大应变均不相同，中、后轴车轮荷载产生的应变(因中、后轴轮距相同，中、后轴车轮荷载产生的最大应变为二者中的最大值)大于前轴车轮荷载产生的应变，且横向应变大于纵向和垂向应变。

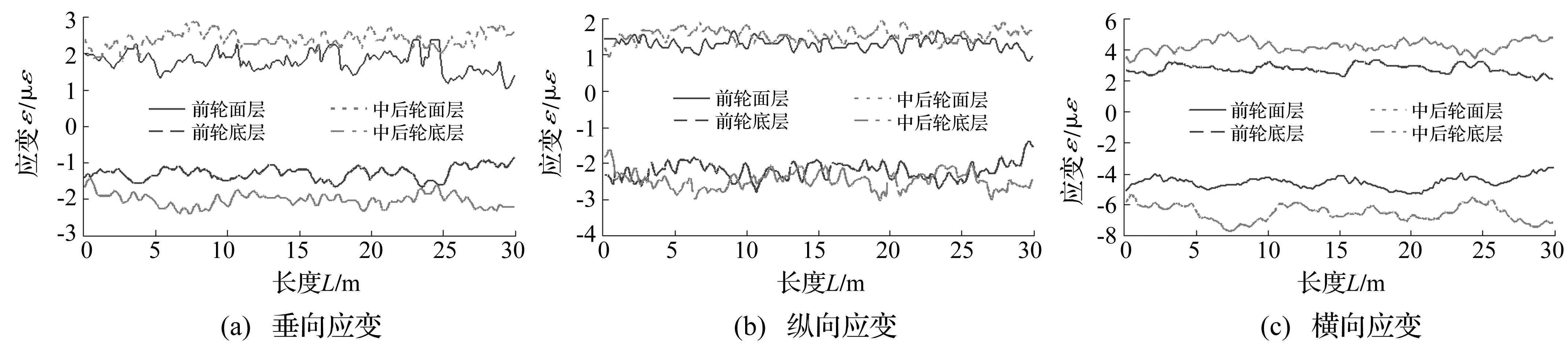
图6 路面长度方向沥青上面层顶面和下面层底面最大应变变化曲线Fig.6 The maximum strain curves of asphalt surface and bottom layer along the length direction

图7为车辆随机动载作用下沿路面长度和宽度方向沥青上面层顶面(SMA13)和下面层底面(Sup25)最大应变变化曲线。

由图7可以看出，车辆通过路面时，在沥青上面层顶面和沥青下面层底面无论是路面长度方向还是宽度方向，各点的三个方向的最大应变均不相同。

5 结 论

(1) 建立了考虑黏弹性的柔性沥青路面三维有限元模型，仿真计算了重型车辆多轮随机动载作用下柔性沥青路面的动态应变响应。

(2) 三轴车辆通过路面时，当车轮接近与离开该位置时，三种沥青材料组成的沥青各层顶面和下面层底面产生的三个方向的应变大小及变化规律均不相同，三个层顶面的三个方向应变变化规律基本相似，垂向应变为拉应变，纵向应变出现拉压应变变化，横向应变为压应变，且横向压应变最大；沥青下面层底面应变变化与各层顶面的应变变化不同，垂向应变为压应变，纵向应变出现压拉应变变化、横向应变为拉应变，且横向拉应变最大。

(3) 在路面长度方向的不同位置，路面三个方向的最大应变均不相同，中、后轴车轮荷载产生的应变大于前轴车轮荷载产生的应变，且横向应变大于纵向和垂向应变。

(4) 车辆通过路面时，沥青上面层顶面和沥青下面层底面无论是路面长度方向还是宽度方向，各点的三个方向的最大应变均不相同。

(5) 研究结果可为柔性沥青路面结构设计与路面寿命分析及预测提供参考依据。

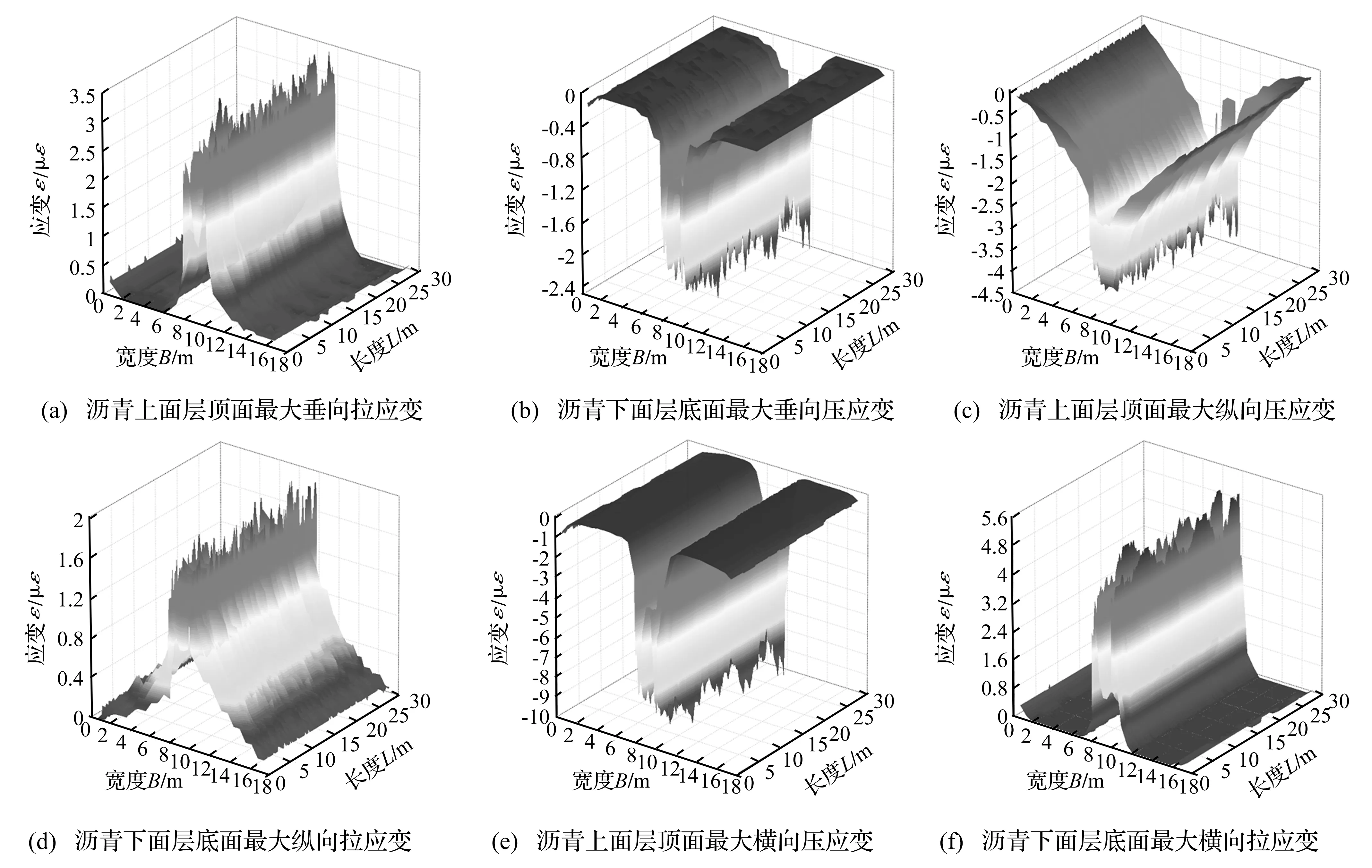
图7 沥青上面层顶面和下面层底面最大应变变化曲线Fig.7 The maximum strain curves of asphalt surface and bottom layer

[1] AL-QADI I L, ELSEIFI M A. Viscoelastic modeling and field validation of flexible pavements[J]. Journal of Engineering Mechanics, 2006, 132(2): 172-178.

[2] WANG H, Al-QADI I L. Combined effect of moving wheel loading and three-dimensional contact stresses on perpetual pavement responses[J]. Transportation Research Record Journal of the Transportation Research Board, 2009, 2095(1):53-61.

[3] WANG Hao, AL-QADI I L．Evaluation of surface-related pavement damage due to tire braking[J]．Road Materials & Pavement Design，2011，11(1)：101-121．

[4] ALI B，SHAHROUR M，SHAHROUR I．Elasto-viscoplastic finite element analysis of the long-term behavior of flexible pavements[J]．Road Materials & Pavement Design，2011，9(3)：463-479．

[5] DE ARAUJ O, JUNIOR P C，SOARES J B，et al．Dynamic viscoelastic analysis of asphalt pavements using a finite element formulation[J]．Road Materials & Pavement Design，2011，11(2)：409-433．

[6] KHAVASSEFAT P. Dynamic response of flexible pavements at vehicle-road interaction[J]. Road Materials & Pavement Design, 2015, 16(2):256-276.

[7] LIN J H．Variations in dynamic vehicle load on road pavement[J]．International Journal of Pavement Engineering，2014，15(6)：558-563．

[8] KHAVASSEFAT P，JELAGIN D，BIRGISSON B．The non-stationary response of flexible pavements to moving loads[J]．International Journal of Pavement Engineering，2015：1-13．

[9] SARKAR A．Numerical comparison of flexible pavement dynamic response under different axles[J]．International Journal of Pavement Engineering，2015：1-11．

[10] BESKOU N D，THEODORAKOPOULOS D D．Dynamic effects of moving loads on road pavements：A review[J]．Soil Dynamics and Earthquake Engineering，2011，31(4)：547-567．

[11] ZHANG Y，ZHANG X．Dynamic response analysis of pavement and subgrade of highmay[C]//Multimedia Technology (ICMT)，2011 International Conference on．IEEE，2011：1034-1036．

[12] 曹卫锋，吕彭民．黏弹性沥青路面车辆动力响应仿真分析研究[J]．计算机仿真，2013，30(4)：173-177．

CAO Weifeng，LÜ Pengmin．Research on simulation analysis of dynamic response in viscoelastic asphalt pavement under moving vehicle loads[J]．Computer Simulation，2013，30(4)：173-177．

[13] 董忠红，吕彭民．移动荷载下黏弹性层状沥青路面动力响应模型[J]．工程力学，2011(12)：153-159．

DONG Zhonghong，LÜ Pengmin．A model to study the dynamic response of visco-elastic layered system under moving load[J]．Engineering Mechanics，2011(12)：153-159．

[14] 张洪亮，胡长顺，许伟清．移动荷载作用下柔性路面的动力响应[J]．长安大学学报(自然科学版)，2005，25(5)：6-10．

ZHANG Hongliang，HU Changshun，XU Weiqing．Dynamic response of flexible pavement under moving load[J]．Journal of Chang’an University(Natural Science Edition)，2005，25 (5)：6-10．[15] 陈恩利，刘永强，赵进宝．移动荷载作用下路面动力响应试验研究[J]．振动与冲击，2014，33(16)：62-67．

CHEN Enli，LIU Yongqiang，ZHAO Jinbao．Experiments on dynamic response of pavement under moving load[J]．Journal of Vibration and Shock，2014，33(16)：62-67．

[16] 廖公云，黄晓明．ABAQUS有限元软件在道路工程中的应用[M]．南京：东南大学，2008．

[17] 赵延庆，钟阳．沥青路面动态黏弹性响应分析[J]．振动与冲击，2009，28(9)：159-162．

ZHAO Yanqing，ZHONG Yang．Dynamic viscoelastic analysis of asphalt pavements[J]．Journal of Vibration and Shock，2009，28(9)：159-162．

[18] 刘祥银，陈洋，高攀，等．双轮辙激励下多轴重型车辆动载特性仿真分析[J]．振动与冲击，2015，34(13)：48-52．

LIU Xiangyin，CHEN Yang，GAO Pan，et al．Simulation analysis for multiaxial heavy vehicles’ dynamic load characteristics under bilateral tracks’ road excitation[J]． Journal of Vibration and Shock，2015，34(13)：48-52．

[19] LIU Dawei, JIANG Rongchao, YANG Yuedong，et al．Simulation study of heavy vehicle road-friendliness under bilateral tracks’ excitation[J]．Advanced Materials Research，2013, 680：422-428．

[20] WEISSMAN S. Influence of tire-pavement contact stress distribution on development of distress mechanisms in pavements[J]. Transportation Research Record Journal of the Transportation Research Board, 1999, 1655(1):161-167.

[21] 陈静. 车辆与路面相互作用的基础研究[D]. 长春：吉林大学, 2002.

Strain analysis of a flexible asphalt pavement under multi-wheel random dynamic loads of vehicles

CHEN Yang, DAI Zonghong, CHEN Huanming, LIU Dawei

(College of Mechanical & Electronic Engineering, Qingdao University, Qingdao 266071, China)

In order to analyze the strain of a flexible asphalt pavement under vehicle random dynamic loads, the finite element model of the flexible asphalt pavement considering its viscoelasticity was established with the finite element analysis software ABAQUS. The flexible asphalt pavement’s strain responses in three directions under multi-wheel random dynamic loads of vehicles were simulated. The strains’ time histories features were analyzed under random dynamic loads of a multiaxial vehicle and the maximum strain of each point on the pavement was obtained. The results showed that the strains of each asphalt layer’s top surface and bottom surface for 3 layers of different asphalt materials are different in three directions and their variations are also different; on the top surface of the upper; layer and the bottom surface of the lowest layer in the longitudinal direction or the width direction, the maximum strains in 3 directions of each point are different; the strains caused by the middle and rear wheel axle loads are larger than those caused by the front wheel axle loads in the longitudinal direction and the transverse strains are bigger than the vertical and longitudinal strains. The results provided a reference for the design of flexible asphalt pavement structures and the analysis of pavement life.

random dynamic loads; flexible asphalt pavement; viscoelastic; strain; FEM

国家自然科学基金资助项目(51475248)

2016-02-14 修改稿收到日期：2016-03-01

陈洋 女，硕士生，1991年10月生

刘大维 男，博士，教授，1957年3月

U416.2

A

10.13465/j.cnki.jvs.2016.19.003