自升式平台2种典型桩靴结构形式对比
2016-11-23陈佳欣
陈佳欣
(上海振华重工集团(股份)有限公司,海上重工设计研究院,上海 200125)
自升式平台2种典型桩靴结构形式对比
陈佳欣
(上海振华重工集团(股份)有限公司,海上重工设计研究院,上海 200125)
以2种具有典型结构设计形式的桩靴为研究对象,依据规范要求进行工况设计与载荷分析,利用有限元软件MSC Patran/Nastran建立有限元模型并进行强度计算,得到各工况下桩靴的应力分布,分析得到预压载工况下接触面积与应力大小的关系以及偏心工况下偏心形式对结构强度的影响,根据有限元计算结果分析2种桩靴的结构性能优势。
自升式钻井平台;桩靴;典型结构设计;对比与分析,有限元方法
自升式钻井平台,具有造价低、海况适应性强等优点[1],是当今海洋油气勘探的主要装备。桩靴是自升式钻井平台主流设计方案中的关键组成部分之一,桩靴的结构设计与强度分析一直是工程项目人员与科研人员关注的研究领域。
国内学者针对某一桩靴结构进行规范校核的研究比较普遍[2-7],但是对于典型桩靴结构之间结构性能比较的研究较少。唐文献等[8]结合有限单元法和尺寸优化理论,认为其所研究的桩靴部分区域材料强度有富余,因此以轻量化为设计目标对桩靴结构进行优化设计,得到桩靴最合理板厚,优化后的桩靴质量得到减轻,并对比了桩靴优化前后的结构性能。该研究为桩靴结构的优化设计提供了一种思路,即在保证强度的前提下,减轻桩靴质量,但是这一优化方式虽然改善了桩靴的应力分布,但也导致了最大应力的上升。
考虑以主流自升式钻井平台的桩靴结构为研究对象,采用2种桩靴典型设计方式进行结构设计,依据船级社规范[9-10]对2种桩靴强度进行有限元分析与计算,对比2种结构设计形式下桩靴的结构性能与特点。
1 2种典型桩靴结构
1.1 结构设计特点与有限元模型
桩靴的平面投影呈现为多边形或者圆形,并且上表面与下表面均带有一定的坡度,以方便桩靴的插桩与拨桩操作。桩靴内部设置有多道环向舱壁,舱壁有局部加强,部分舱壁设置有开孔以方便人员进出和减轻结构自重。桩靴与桩腿的连接方式主要有2种:①桩腿与桩靴在其外围舱壁处进行连接,并在顶部设有支撑舱壁与桩腿斜撑杆连接;②在桩靴顶部整个桩靴框架范围内设立主要支撑舱壁并延伸至桩靴内部舱壁,与桩腿弦杆以及斜撑杆进行连接。将研究对象分别命名为桩靴A与桩靴B。桩靴A为多边形平面投影,并采用第一种桩靴与桩腿连接方式,桩靴B为圆形平面投影,桩靴与桩腿的连接采用第二种方式。2种桩靴有限元模型见图1。桩腿为三角形桁架式结构,桩腿三根弦杆在桩靴上的投影见图2中实心圆所示,图中实线为桩靴主框架。

图1 桩靴结构有限元模型
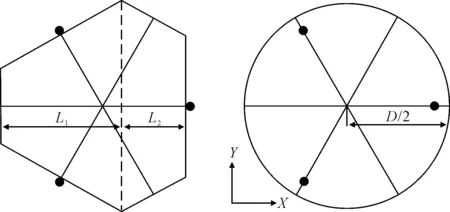
图2 桩靴、桩腿平面投影
1.2 材料属性与校核标准
桩靴A与桩靴B采用材料主要为AH36、DH36和EH36钢,桩靴A的桩腿连接及支撑结构采用了EQ63钢,桩靴B的桩腿连接支撑结构与桩腿弦杆相交附近采用了EQ56钢。根据规范,AH36、DH36和EH36钢的屈服强度为355 MPa,考虑安全系数1.11,动载荷许用应力为320 MPa; EQ63钢和EQ56钢的屈服强度分别为620 MPa和550 MPa,考虑安全系数1.11后,动载荷许用应力分别为558 MPa和495 MPa。
1.3 边界条件
根据规范要求,边界条件为顶端桩腿简支约束,同时为了消除边界条件的影响,桩腿从桩靴开始向上延伸7节。考虑到桩靴实际受到海底土壤约束,亦可以采用桩靴底部弹簧约束的边界条件处理方式,但是考虑到通常情况下很难掌握完整的土壤资料,并且不同海域还不完全相同,同时涉及到非线性接触问题,计算量较大且很难保证所得结果准确,从而造成边界条件设置错误,影响到最终的结果。这里采用传统与规范推荐的上部桩腿简支约束边界条件,以桩靴B为例,给出边界条件施加示意,见图3。

图3 边界条件
2 载荷与工况
2.1 预压载工况
考虑到桩靴与海底接触面积存在很多可能性,从桩靴底部中心区域接触海底地基到接触面积扩大到整个底部这一连续过程中选取几组状态进行分析。按照接触面积占总面积的百分比进行工况设计,包括10%、25%、50%、75%和100% 5种状态。根据技术规格书和该型平台总强度计算报告,预压载工况下每个桩靴承受的最大垂向力为106 389 kN,具体计算过程见式(1)。根据力的平衡原理计算出不同接触面积时桩靴底部所承受的均布支反压力。同时,考虑到2种不同结构设计形式的桩靴所具有的总接触面积不一样,因此所承受压力不完全相同。该工况设计载荷见表1。
(1)
式中,W1——空船提升重量;
W2——预压载重量;
W3——桩靴自重与其中压载水重量之和;
W4——桩靴所受浮力;
W5——桩腿所受浮力;
W6——可变载荷;
W7——桩腿重量。
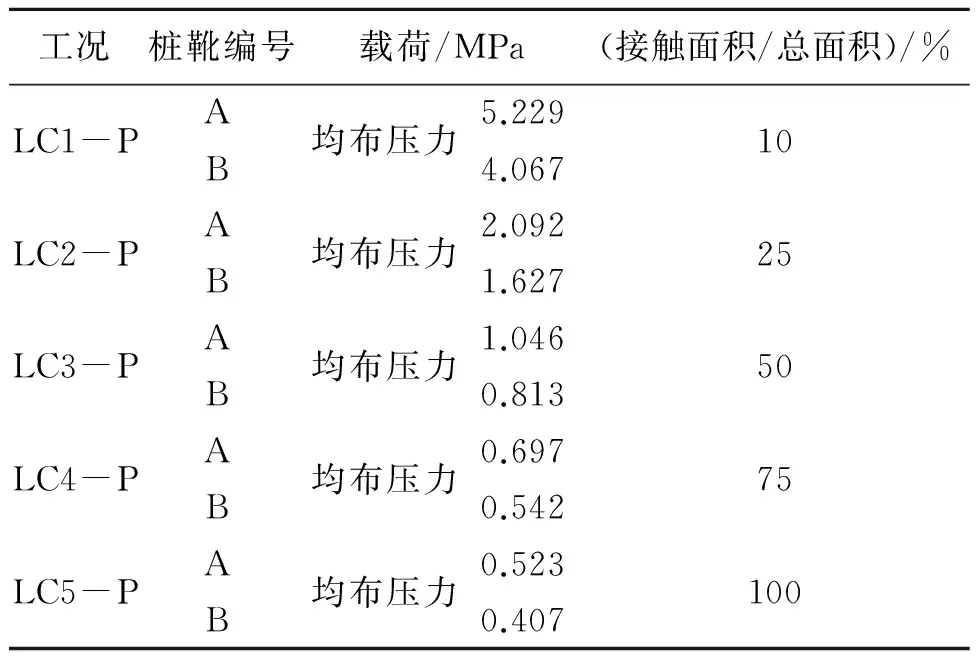
表1 预压载工况设计载荷
2.2 偏心工况
考虑到海水冲刷、海底不平整等因素,会导致桩靴受到偏心载荷影响[11],考虑50%的冲刷面积,相当于50%的面积承受压力,同时考虑2种偏心形式,见图4,该工况下设计载荷见表2。

图4 偏心工况下压力分布区域
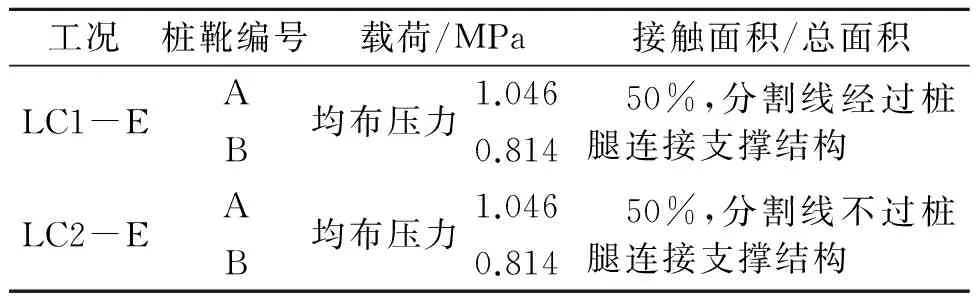
工况桩靴编号载荷/MPa接触面积/总面积LC1-EAB均布压力1.0460.814 50%,分割线经过桩腿连接支撑结构LC2-EAB均布压力1.0460.814 50%,分割线不过桩腿连接支撑结构
2.3 风暴自存工况
风暴工况下平台承受较为恶劣的环境载荷,需要考虑平台重力,以及包括风、浪、流在内的环境载荷。根据规范要求,桩靴承受载荷主要包括自存工况最大垂向力FV、水平力FH和35%下导向处的倾覆力矩MOTM,由于环境载荷,以反力形式施加在桩靴底部,实际加载的载荷应与环境载荷大小相同、方向相反。其中,将力矩M(35%MOTM)转化成力并与最大垂向支反力FV叠加,以三角非均布压力载荷的形式施加到桩靴底面,具体载荷施加示意如图5所示。最大垂向力FV计算原理与下式类似,相应水平载荷FH和35%下导向处的倾覆力矩MOTM根据该型平台总强度计算报告得到,该工况下设计载荷见表3。

图5 风暴自存工况下施加载荷

载荷备注垂向最大支反力61550kN水平最大支反力4448kN35%最大计算力矩474550kN·m 接触面积/总面积=100%
简化后的压力分布以如下形式表示。
桩靴A:P(x)=k1x+b1,-L1 桩靴B:P(x)=k2x+b2,-D/2 其中:L1,L2为桩靴A底面长度方向投影两端距折角距离,桩靴总长L=L1+L2,见图2。 由于桩靴有折角,折角两边直线方程不同,为计算方便,取折角处为积分原点,再得到三角载荷方程后通过移轴定理得到根据中心轴的三角载荷方程;D为桩靴B底面的投影直径,见图2。 分别对2种桩靴在整个积分域上对x=L2和x=D/2取矩,积分的结果即为一个桩靴所承受的弯矩M,在整个积分域上的三角载荷在Z向的矢量和即为垂向支反力V,固可联立方程组解出三角载荷方程。 对于桩靴A,桩靴两折边以折角处为原点的直线方程分别为 (1) 式中:B——桩靴A最大宽度; Bfwd,Baft——桩靴A前段和后端宽度。 计算可得桩靴A承受的三角载荷为f(x)=0.887×10-5x-0.287;桩靴B承受的三角载荷为f(x)=-1.537×10-5x-0.242。载荷方程均以中心轴为原点,其中x单位为mm,载荷单位为MPa,将相应载荷以压力场的形式施加于桩靴底部板全表面。 3.1 结果比较 根据表1~3,分别针对桩靴A、B进行有限元强度分析,将结果进行对比并汇总于表4中。由表4可见,不同工况下2型桩靴应力大小呈现出相近的趋势,风暴自存工况下虽然环境载荷影响较大,但是平台可变载荷小,相比较于预压载工况和偏心工况最大应力较小。 表4 最大应力 MPa 预压载工况下压力变化见图6。桩靴A主体结构应力普遍高于桩靴B主体结构,而桩靴A的桩腿连接支撑结构应力普遍低于桩靴B,考虑原因是圆形结构设计下结构连接过渡较为平稳,桩靴主体应力分布更加均匀,主体上表面应力集中区域或是结构连接角隅处较少;而桩靴B的桩腿连接支撑结构是由桩靴内部舱壁升高的三角形区域承载,桩腿弦杆和斜撑都与之相连,在桩腿连接结构面板、舱壁、桩腿和弦杆相交的区域会出现一定的应力集中。此外,随着接触面积的扩大,桩靴A与桩靴B最大应力变化规律相近,都是随着接触面积的扩大先上升后下降,最大应力发生在接触面积为总面积25%的情况下。 图6 预压载工况下应力变化规律 由表4可见,偏心工况是桩靴结构设计的主要控制工况,虽然同预压载工况LC3-P一样是底面有一半的接触面积,但是因为接触面积的不对称性,导致应力相比较LC3-P有明显增大,其中LC2-E工况的偏心形式更为危险(见图4),即平分线不经过桩腿连接支撑结构,以偏心工况LC2-E为例给出桩靴A与桩靴B在此工况下的应力分布见图7。 图7 偏心工况应力分布 3.2 结构设计讨论 从桩靴A和桩靴B在各个工况下所展现出的结构性能可以看出,当底部采用圆形设计时,桩靴在插桩过程中会表现出更好的强度性能,应力分布更为均匀,在产生偏心影响时,圆形底部设计更为可靠。从表4可以看出,桩靴主体部分与桩腿连接、支撑结构相比是偏于安全的,危险区域还是桩腿连接支撑部位,当采用桩靴A的支撑连接形式时,各工况下该区域应力大小均小于桩靴B的连接方式。因此,在今后桩靴结构设计中,可以结合这2种桩靴结构设计形式的优点,采用圆形轮廓进行桩靴主体设计,在与桩腿的连接方式上采用桩靴A的形式,即弦杆与桩靴主体在外部连接,桩靴顶部设斜撑杆支撑壁。 1)偏心工况是桩靴结构设计的主要控制工况,由于偏心载荷的影响,该工况下,桩靴主体部分和桩腿连接部分应力均较大。此外,当偏心分界线不经过桩腿弦杆及其连接与支撑结构时,结构最为危险; 2)预压载工况下,随着受力接触面积的扩大,桩靴应力分布情况和应力峰值会逐渐得到改善,但是桩靴A会在接触三角形面积与桩腿弦杆所围三角形面积相近时应力达到峰值,然后逐渐减少。总体上,桩靴B主体部分应力分布更为均匀,应力峰值也较小; 3)桩靴与桩腿的连接、支撑区域应力普遍较大,是结构设计中需要重点关注的区域,桩靴A相比较于桩靴B,在该区域的应力较小、分布也更为均匀,设计方式更为合理; 4)在今后自升式钻井平台的桩靴结构设计中可以借鉴上述2种典型设计方式的优点,对提高平台的安全性、稳定性以及作业能力都有帮助。 [1] 李润培,王志农.海洋平台强度分析[M].上海:上海交通大学出版社,1992. [2] 郭志彬,杨琼,宋雄伟,等.自升式平台桩靴强度分析[J].船舶工程,2012,34(2):76-78. [3] 许靖,白锐利,马小平.自升式钻井平台桩靴结构分析[J].船舶工程,2012,34(3):76-79. [4] 华晓涛,金晶.自升式平台桩靴的有限元分析[J].船舶工程,2013,35(增刊2):106-109. [5] 李永超,孙雪荣.自升式钻井平台桩靴结构强度分析[J].船舶与海洋工程,2014(3):10-14. [6] 伞立忠.自升式钻井平台桩靴结构设计[D].大连:大连理工大学,2012. [7] 孙雅楠.自升式海洋平台桩靴强度分析[D].大连:大连理工大学,2013. [8] 唐文献,秦文龙,张建,等.自升式平台桩靴结构优化设计[J].中国造船,2013,54(3):78-84. [9] ABS. Rules for building and classing mobile offshore drilling units[S].ABS,2014. [10] 中国船级社.海上移动平台入级规范[S].北京:人民交通出版社,2012. [11] 张建,唐文献,秦文龙,等.偏心受压工况下自升式平台桩腿力学性能研究[J].中国造船,2013,54(2):111-117. Comparison and Analysis of Two Typical Types of Self-elevating Unit Spudcan Structures CHEN Jia-xin (Offshore Heavy Industry Design Institute, Shanghai Zhenhua Heavy Industries Co. Ltd., Shanghai 200125, China) Taking two types of jack-up unit spudcan with typical design as examples, the load cases were designed and the loads were calculated based on related rules. The FE models of two types of spudcan were established to carry out the strength calculation and check by MSC Patran/Nastran. Based on the preload condition, the relationship between the contact area and the maximum stress can be obtained. According to the eccentric condition, the influences of different eccentric types on strength can be witnessed. The structural performance of these two types of spudcan was compared with to analyze the advantages of each spudcan. jack-up drilling unit; spudcan; typical structural design; comparison and analysis; finite element method 10.3963/j.issn.1671-7953.2016.05.037 2016-01-13 陈佳欣(1989—),女,硕士,助理工程师 U674.38;P751 A 1671-7953(2016)05-0146-05 修回日期:2016-02-19 研究方向:船舶与海洋工程结构性能分析 E-mail:cjx19891119@126.com3 结果讨论



4 结论
