基于隐马尔可夫链模型的软件维护性评估方法研究

郝学良，朱小冬，叶　飞

（军械工程学院，石家庄　050003）

基于隐马尔可夫链模型的软件维护性评估方法研究

郝学良，朱小冬，叶飞

（军械工程学院，石家庄050003）

针对当前软件可维护性评估主观性强，可操作性弱等问题，提出了定量描述维护性的维护时间统计概率描述方法，引入隐马尔可夫链（HMC）模型对维护性状态变迁过程进行描述，以可度量的维护性内部属性影响因素集量化值为观测序列，以维护时间统计概率为状态序列，构造了反映可维护性状态转移的HMC模型；收集配置管理库中软件模块历史维护时间从而确定完成维护任务频率来估计软件维护性初始状态，利用复杂网络特性计算软件维护性影响因素集的量化值，理论上即可评估出当前软件所处的维护性状态，最后运用实例对模型进行了训练与评估；结果表明，利用模型评估出的概率与实际维护任务统计出的可维护性概率基本一致，说明该方法可行且可重复，具有一定实践意义和研究前景。

软件维护性；隐马尔可夫链模型；模糊推理；信息融合；软件维护性评估

0　引言

软件维护性是软件质量的重要属性之一，它在很大程度上直接决定了软件的后期维护成本。提高软件产品的维护性已成为软件生产方和使用方的共识。软件维护性的评估是软件维护性控制和改进的基础，已成为近年来软件维护性研究的热点和难点。

Oman维护性指数 （Maintainability Index，MI）［1］通过方程式计算出来一个经验数值，在一定程度上反映了软件维护性的好坏，但是很难在实际工程中应用。Misra（2005）［3］等基于线性回归技术的软件维护性预计模型，一定程度实现了软件设计阶段的维护性预计方法，Thwin（2005）［4］等运用人工神经网络建立了软件维护性预计模型，将人工智能方法应用到了软件度量领域；Fenton［5］等将贝叶斯网络应用到软件度量与预计研究当中，提出处理不确定性问题的方法，将专家经验与知识结合起来，实现对变量间复杂关系的建模。目前关于软件维护性评估方法的研究存在定性研究多，定量研究少；主观判断多，数据验证少的特点，仍停留在软件维护性的内部属性度量阶段，缺乏外部属性和内部属性结合的综合研究。针对以上问题，本文提出了一种基于配置管理库数据的软件可维护性评估方法，将实际维护过程中的维护性外在表现信息与维护性度量工具所试题的内部度量集结合起来，实现软件维护性的整体评估。

1　软件可维护性的定义及描述方法

1.1基于配置管理库数据的维护性评估可行性分析

软件从用户需求到开发再到发布，在需求的导引下反复维护，更新，是一个不断循环的生命周期过程。

由于软件开发配置管理库中记录了开发过程中软件开发工作量等数据，我们可利用其中的维护时间数据进行维护性度量，以可维护度及平均功能维护时间作为软件维护性评估的指标，并在实际维护活动中统计是否能按时完成任务的频率来估计维护性状态概率，理论上可以实现软件维护性的评估。再选取相应的配置管理库中的数据生成样本库，即可实现对维护性状态估计模型进行训练。利用训练好的模型从配置管理数据库中的模块进行评估，即可实现软件可维护性评估的目的。软件的开发过程本身就可以看作是一个不断进行维护的过程，在项目开发的初级阶段，往往对软件的需求认识不够清晰，使得开发项目难于一次开发成功，即使认识足够清楚，任何个人或团体都可能会出错或疏漏，因此，在软件开发过程中出现返工再开发的情况在所难免。开发的第一次经常是试验开发，其目标在于探索可行性，弄清软件需求，而第二次的开发实际上就既是开发又可看作是对第一次的维护，常见的 “演化模型”和“螺旋模型”就是这种典型的开发过程。配置管理工具正是贯穿软件开发与软件维护的一个重要的桥梁。配置管理作为软件过程管理的重要工具，不仅可以保证软件开发活动的高效，准确完成，更起着保证软件具有良好维护性的作用。

1.2软件维护过程中的维护性内部影响因素集分析

软件维护性影响因素主要有四大类：软件基本属性（software basic attribute）、源代码设计特性（source code attribute）、文档特性（document attribute）和管理因素（management attribute），其中软件本身的设计特性从根本上决定了软件维护性的好坏。其中，前三类因素可以利用利用粗糙集原理对软件维护性影响因素进行筛选，得到软件的维护性影响因素集包括：规模、结构化因子、复杂度、耦合度、内聚度。并利用模糊推理原理，依据软件系统复杂网络特性与影响因素集之间的关系，实现维护性影响内部因素对软件可维护性影响的定量化描述［6］。

但是对于第四类因素，管理因素，如维护机构的运行机制，人员的水平等很难体现出来。本文所构建的HMC模型正是基于这一最难度量的维护性影响因素进行量化。

典型的软件维护过程一般是由用户需求更改发起的。首先由用户方将更改需求明确为问题报告，提交给软件维护人员，一般是开发人员。由软件维护人员对用户需求进行分析，进一步定位到具体的功能块，在配置管理中则是定位到具体的配置项，这一步即是问题报告分析时间。之后可以制定软件维护计划，以保证有效的软件维护实施和可靠的软件维护质量。在软件维护计划中，要定义软件维护目标、人员和资源分配、组织机构和保障措施等，而且要分析和制定、确认软件维护的策略、流程和和规则、实施方法和工具等。接下来进行的工作即是对源代码进行理解，对于开发人员来说，这一步所耗费的时间一般不会太多。软件完成更改后，再进行回归测试，如果满足用户需求即可发布新版本，此时维护过程完成。

软件的维护性与软件的规模密切相关，通常情况下，规模越大，维护难度越大。同时，软件的维护性在某种程度上也取决于软件的复杂度，同等规模下，软件的设计越复杂，越难以维护。

软件维护的难易大小，成本高低，主要取决于软件维护时间，而维护时间主要包括：更改请求（问题报告）分析时间、软件理解时间、故障定位时间、更改规划及更改影响分析时间、更改实施时间、回归测试时间以及其它的管理延迟时间等。

软件维护时间的长短与目标软件基本属性（成熟度、软硬件运行环境等）、源代码设计特性（结构复杂度、代码质量等）以及文档特性（完整性、一致性）有着直接的关系，另外还与人员技术水平、辅助工具等非软件系统本身因素有关，我们将这些因素统称为管理因素。

1.3三态可维护性状态概率描述

根据GJB中可维护性的定义，本文将软件的维护性状态定义为三态，分别为易维护（s0）、可维护（s1）和不可维护（s2）。具体在工程实际中，假设在规定组织环境内，计划完成维护任务时间或者平均分配到每个模块上的完成时间为T，且在一定的延误时间区间内也可算作按时完成，引入容忍因子α，容忍延误时间Δt=T*α，实际完成维护任务时间为t，对3种状态作如下定义。

1）易维护状态：

对于一个软件或功能块在规定的维护条件下如果能够提前完成维护目标，那么认为该软件或功能块处于易维护状态，根据前面对各时间的定义，即t∈（0，T）；软件处于易维护状态s0的概率为P（s0）=P（t＜T）。

2）可维护状态：

对于一个软件或功能块如果能够在一定容忍延误程度内，按时完成维护目标但是也没有提前完成，那么认为该软件或功能块处于可维护状态s1，根据前面对时间的定义，有t∈［T，T+Δt），软件处于可维护状态的概率为P（s1）=P（T≤t＜T +Δt）；

3）不可维护状态：

对于一个软件或功能块如果在规定的条件下，不能按时完成维护目标，则认为该软件处于不可维护状态，即t∈（t，∞），软件处于不可维护状态s2的概率为P（s1）=P（t＞T）。

由概率和数理统计可知，概率可以用频率来估计，假如在对某软件系统进行维护，该软件系统中的某个子模块，计划完成维护任务时间为T，容忍延误时间Δt=T*α，在时间区间（0，T）内有r次完成维护任务，达到维护目标；在时间区间（T，T+Δt）内有l次完成维护任务，达到维护目标；其余维护时间均落于区间（T+Δt，∞）。

根据三态可维护性状态描述可得软件处于3种维护状态的概率分别为：

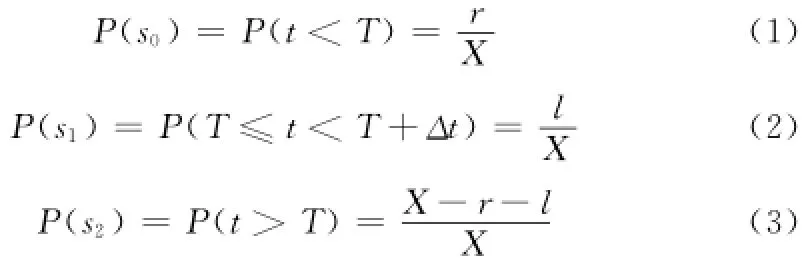
2　软件维护性状态转移模型

软件维护性既是一种内部属性，主要受规模、结构化因子、复杂度、耦合度、内聚度等内部因素影响，同时也是一种外部属性，受维护组织，人员，策略等影响。因此，在软件更改维护的过程中，会牵一发而动全身，随着各影响因素的变化，其维护性也会变化，即软件的维护性状态随着软件的演化是动态变化的，对于其维护性的评估也不能静止地去考虑。因此，引入隐马尔可夫链模型来识别多种维护性影响因素集下的软件维护性状态随着软件更改而产生的转移变迁过程。

2.1HMC模型在维护性评估中的应用

最简单的隐马尔

可夫模型一般用一个五元组来表示：

λ=（N，M，A，B，π）（4）

其中，N表示状态数，记N个隐状态为θ1，θ2，…，θN，t时刻马尔可夫链所处的状态为q，且q∈｛θ1，θ2，…，θN｝；M为每个状态对应的可观测值数目，记M个观测值为v1，v2，…，vM，t时刻观测值为ot且ot∈｛v1，v2，…，vM｝；隐状态的初始概率分布为π=（π1，π2，…，πM），其中π=P（q=θi），1≤i≤N；A为状态转移概率矩阵，A=｛aij｝N×N，其中aij= P（qi+1=θjqi=θi），1≤i，j≤N；B为观察值概率矩阵，B =｛bjk｝N×M，其中bjk=P（oi=vkqt=θj）。

综上，H MC模型通过状态转移矩阵A、观察值矩阵B和初始状态π的分布来描述双重随机过程［7］。H MC在实际应用过程中经常会用到3个常用的算法，如表1中所示。

在解决本文所提出的维护性状态评估问题中，利用配置管理库中的维护性统计数据作为模型的初始状态，用维护性度量工具度量软件的内部维护性影响因素量化值作为观测序列，采用Baum-Welch算法对模型参数进行训练，对训练后的模型再应用Forward-Backward算法计算输出概率，即可得到软件的维护性状态概率。

2.2软件维护性状态转移模型

软件维护性是软件的一种能力，这种能力在软件设计阶段即已初步形成，在软件的开发过程中逐步确定下来，但是由于软件的维护不像硬件维修那样简单替换，而是存在不同程度的波及效应，因此软件的影响因素集及软件的可维护性状态都会随着软件维护的递进而发生改变，这个过程即是一个隐马尔可夫状态转移过程。

1）三态维护性状态转移模型：

前面已提到把软件系统的可维护性隐性状态分为3个，分别为：易维护状态、可维护状态、不可维护状态，这3种状态的转移过程可以图1来表示，纵轴表示可维护性状态的分布，横轴表示软件维护基线或维护进程的更迭。

结合软件三态维护性的概率表达，表1表达了软件维护性状态概率分布。

2）软件维护性影响因素集概率化表示：

利用粗糙集原理对软件维护性影响因素进行筛选，得到软件的维护性影响因素集包括：规模、结构化因子、复杂度、耦合度、内聚度。并利用模糊推理原理，依据软件系统复杂网络特性与影响因素集之间的关系，实现维护性影响因素对软件可维护性影响的定量化，再综合各影响因素值进行归一化处理，即得到软件维护性的观测状态值［6］。

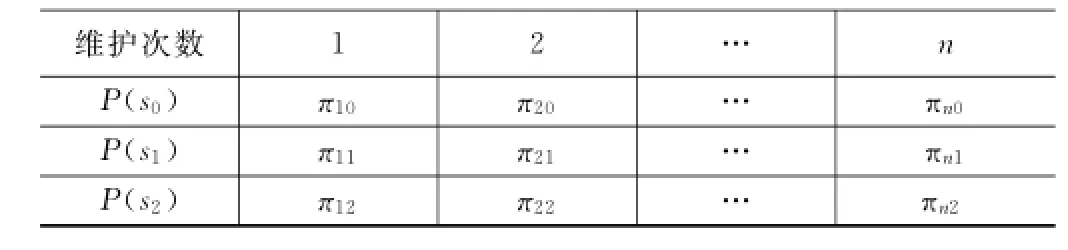
表1　维护性状态转移矩阵

2.3基于模糊推理的影响因素集量化

将软件规模、结构化因子、复杂度、耦合度、内聚度等5个影响因素与软件体系结构的复杂网络特性建立关系，并对每一个影响因素建立模糊推理系统；利用Pajeck分析软件模块的复杂网络特性，将复杂网络特性的取值作为模糊系统的输入，根据理论最好值与实际值的范围建立分级标准；确定输入输出变量后，以内聚度作为度量示例，建立模糊推理系统。

2.4HMC模型改进及训练

由于软件维护性的状态发展具有渐进的过程，建立HMC维护性评估模型，实质上是通过状态转移矩阵来对维护进程中的状态转移进行描述。对于这样一个矩阵，其初始状态往往不能精确获取，而是通过优化训练算法来得到状态转移矩阵，从而再通过求解HMC过程来实现评估。但是从理论上仍存在以下两个问题［9］：

1）HMC初始模型的选取问题仍未完全解决。实际情况中软件的可维护性状态经常处于变化当中，初始模型的选择不当必然会对最终的评估结果造成影响。

2）HMC模型的训练问题在整个评估模型中起着重要作用。经典的重估公式假设条件与实际应用中出入较大，可能会造成收敛速度慢甚至无法完成训练。

针对HMC模型存在的上述两个问题进行改进，以提高软件可维护性状态的识别速度与精度。可利用改进的参数重估公式进行多观测序列模型训练，重估公式如式（5）所示［8］。由于当前软件的维护数据较少，反映软件可维护性状态的信息也比较少，可通过历史维护数据来初步评估软件的可维护性。

现阶段的软件的维护更改过程并不是针对维护性进行的，所以软件维护性的状态是渐变的没有明确的界限。

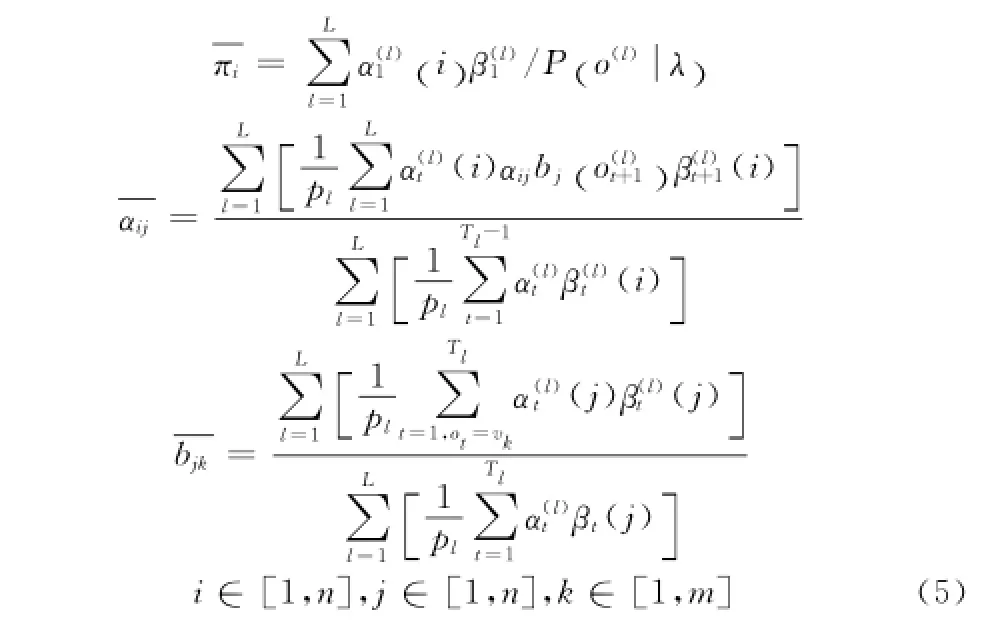
假设软件系统由n个模块组成，记为N=（1，2，…，n）；每个模块都具有m种状态，记为M=（1，2，…，m）；各模块的可维护性状态概率记为P ，显然有：

宠物放置在一边并局部消毒。从前臂头静脉采集2毫升静脉血作血液检查。首先，采血部上部与止血带结扎，静脉怒露。用酒精棉球消毒静脉血管。然后将针和皮肤以45度角皮下穿刺。然后将血液推入EDTA－K2抗凝管。最后，用自动流式细胞仪分析和检测血样并进行打印。结果包括离子检查和血常规检查。

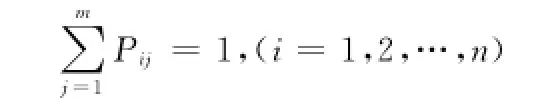
假设软件在初始状态下处于可维护状态，则初始状态的可维护性概率分布为π0=（0，1，0），状态转移概率矩阵A0和影响因素观测值矩阵B0采取均匀方法选取，代入式（4）得到初始的H MC模型λ0= （A0，B0，π0）。将归一化处理后的影响因素集的值作为观测序列输入到初始模型λ0=（A0，B0，π0），利用Baum-Welch算法得到软件的动态HMC模型λt=（At，Bt，πt），利用前向-后向算法计算不同模块的影响因素集的量化值在给定模型λt=（At，Bt，πt）下的概率P（o|λ），反复训练，直到该概率值收敛，此时的H MC模型即可以用来评估软件可维护性状态。

令Pj（t）=P（qt=j）表示软件维护性在t时刻处于j状态的概率。根据切普曼-科尔莫哥洛夫微分方程，可以得到P′（t）=P（t）A，求解该微分方程可以分别得到软件维护性处于3种状态的概率P（s0），P（s1），P（s2）。通过这3种状态概率可以对软件的维护性进行评估。

3　实例验证

3.1维护性数据收集与模型求解

“美腾”是我课题组自行开发的虚拟维修训练软件，包含系统登录、信息建模以及信息管理等12个模块，其版本已更新至V3.0。

在V2.0至V3.0的更新开发过程中，以“训练内容”模块为例，在配置管理工具中对每次维护都记录了检出（Check out）和检入（Check in）时间，与开发维护人员的沟通，剔除自然时间中的非工作时间，得到检出和检入时间差作为进行一次维护的实际工作时间，实际数据的处理过程如下：其检出时间为2010.04.08 09：18，检入时间为2010.04.08 16：30，通过与开发人员的沟通，每天工作时间8小时，上班时间为上午八点到十二点，下午两点到六点，实际工作时间为：

2010.04.08 09：18到2010.04.08 12：00；

得到此次维护的维护时间为5小时。而维护计划时间为8小时，容忍时间为2小时，因此该模型的可维护性状态属于易维护。对该模块的维护记录数据收集如表2所示。

由表中数据可以统计出，该模块的可维护性处于3种状态的概率分别为P（s0）=60%，P（s1）=30%，P（s2）=10%。将π0=（0.6，0.3，0.1）作为初始状态概率代入式（4），利用参数重估公式（5）对模型进行训练，得到反映实际维护性状态转移的H MC模型。运用训练好的模型对各模块的后10次维护过程进行跟踪对比验证，结果如表3所示。

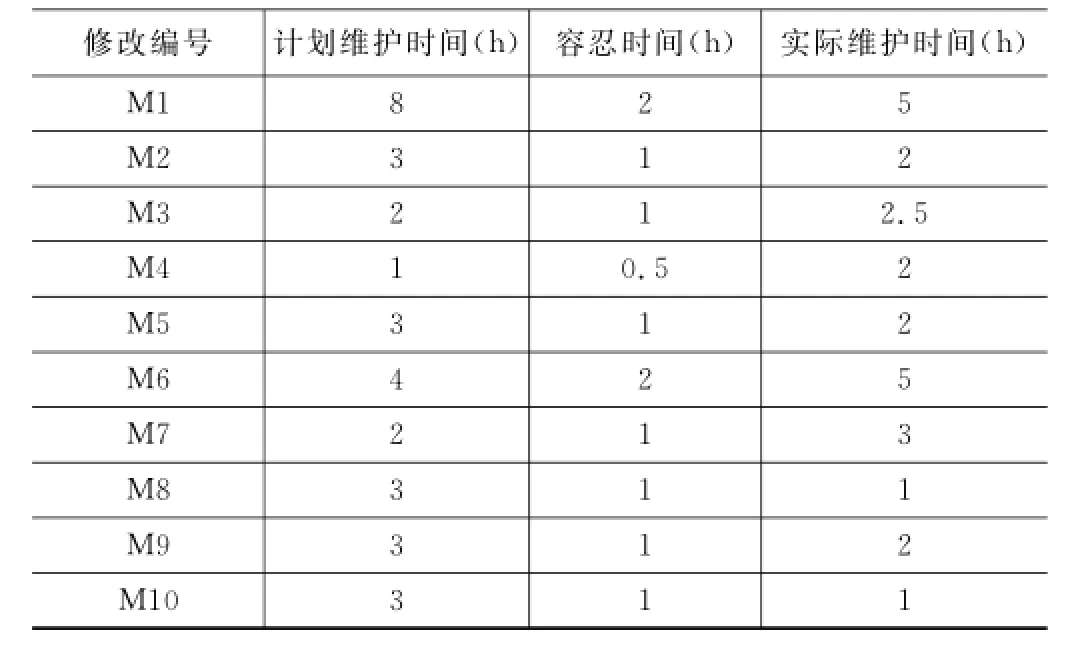
表2　“训练内容”模块维护时间数据收集

表3　评估结果分析

3.2结果分析

从计算结果中可看出，模型所预测出的软件维护性状态概率与实际维护进程中软件的可维护性状态概率基本一致，所测试的软件模块处于易维护性状态。

4　结论

针对软件维护性定量评估依赖主观经验多，可操作性弱，评估稳定度低下的问题，提出了一种软件维护性评估的新方法。建立可维护性状态转移模型，不仅能够对维护进程中的不确定信息进行处理，同时，该模型能够充分利用反映维护性外部表现的历史维护数据和软件规模、复杂度等软件自身的设计特性对软件系统进行合理的评估。实例分析表明，本文提出的方法是有效的，易于实施且具有可重复性。

［1］Oman P.and Hagemeister J.Metrics for Assessing a Software System's Maintainability［A］.In proceedings of Conference on Software Maintenance［C］.IEEE，1992.

［2］Misra，S.C..Modeling design/coding factors that drive maintainability of software systems［J］.Software Quality Journal 13（3），2005：297-320.

［3］Thwin，M.M.T.，Quah，T.S..Application of neural networks for software quality prediction using object-oriented metrics［J］. Journal of Systems and Software 76（2），2005：147-156.

［4］Fenton N E，Krause Paul Neil M.Software measurement：uncertainty and causal modeling［J］.IEEE Software 19（4），2002：116-122.

［5］Sussy B，Jose A，Gonzalo C，eta al.Critical success factors taxonomy for software process deployment［J］.Software Qual J，2014（22）：21-48.

［6］吴军，邵新宇，邓超.隐马尔可夫链模型在装备运行可靠性预测中的应用［J］.中国机械工程，2010，21（19）：2345-2349.

［7］蔡金锭，鄢仁武.ARMA双谱分析与离散隐马尔可夫模型在电力电子电路故障诊断中的应用［J］.中国电机工程学报，2010，30（24）：54-60.

［8］黄景德，郝学良，黄义.基于改进H MM的潜在电子故障状态识别模型［J］.仪器仪表学报，2011，32（11）：2481-2486.

［9］冷晓艳，刘宇，段俊斌，等.装备软件综合保障研究［J］.计算机测量与控制，2013，21（10）：2750－2752.

［10］杜晶，杨叶，王青，等.基于证据的可信软件过程评估方法［J］.计算机科学与探索，2011，5（6）：501-512.

［11］李明树，杨秋松，翟健.软件过程建模方法研究［J］.软件学报，2009，20（3）：524-545.

Software Maintainability Modeling and Assessment Method Research Based on Hidden Markov Chain Model

Hao Xueliang，Zhu Xiaodong，Ye Fei
（Ordnance Engineering College，Shijiazhuang050003，China）

In order to meet the demand of software maintainability assessment，three-state probability description method was put forward.Hidden Markov Chain model was introduced to estimate maintainability of three-state software，and state transform model was built up.Historical maintenance time of software module was collected from configuration management database to ascertain frequency of success maintenance so as to estimate software maintainability.Affecting factors set value was computed through Fuzzy inference theory.The estimation model was trained and validated through real software case，and the result shows that this method is feasible and repeatable，and can be further studied.

software maintainability；hidden Markov chain model；fuzzy inference；information fusion；software maintainability assessment

1671-4598（2016）05-0284-03

10.16526/j.cnki.11-4762/tp.2016.05.078

TP311.5

A

2015-09-01；

2015-12-08。

装备部重点预研项目“软件保障技术”（编号不公开）。

郝学良（1984-），男，河北省邯郸市人，博士研究生，主要从事软件工程理论与应用技术方向研究。