GNSS载波多普勒频移计算、分析及实验验证

杨　茜，秦红磊

（北京航空航天大学，北京　100191）

GNSS载波多普勒频移计算、分析及实验验证

杨茜，秦红磊

（北京航空航天大学，北京100191）

全球卫星导航系统信号处理中，多普勒频移至关重要；文章对地心惯性坐标系下载波多普勒频移最大值计算进行了研究，其推导中没有考虑地球自转速度和地面用户位置的影响；文章针对这个问题进行分析，通过建立卫星和用户位置和速度之间的立体几何模型，提出了地心地固坐标系下任意用户位置载波多普勒频移最大值的精确计算方法；同时针对多普勒频移计算问题，通过构建卫星与用户之间的距离向量，提出了基于精密星历的任意用户位置载波多普勒频移计算方法；最后使用GNSS仿真数据和实测数据进行验证，两种方法的计算结果均和实验结果相符合；两种新方法能够解决地心地固坐标系下特定位置处的多普勒频移最大值和特定位置处载波多普勒频移的计算问题。

全球导航卫星系统；多普勒频移；地心惯性坐标系；地心地固坐标系；最大值

0　引言

GNSS（global navigation satellite system，GNSS）卫星与地面用户之间存在径向运动，从而产生多普勒频移［1］。多普勒频移在GNSS信号处理中至关重要。接收机捕获的频率搜索范围一般设置为多普勒频移可能取到的最大值［2］，所以载波多普勒频移最大值对伪码捕获速度和载波锁定速度尤其重要。现有的文献和接收机中均引用James Bao-Yen TSUI［2］推导的载波多普勒频移最大值作为载波频率搜索范围，其推导是在地心惯性坐标系（earth-centered inertial coordinate system，ECI）基础上建立，没有考虑地球自转对径向运动速度的影响，而且没有考虑地面用户位置对多普勒频移最大值带来的影响。由于卫星轨道并不是圆轨道，所以卫星高度也不是Tsui推导中的固定值。本文首先对TSUI推导进行修正，主要考虑卫星高度对载波多普勒频移最大（小）值的影响以及计算地心地固坐标系（earth-centered earth-fixed coordinate system，ECEF）下任意用户位置载波多普勒频移最大（小）值；其次是计算任意用户位置的载波多普勒频移；最后是通过GNSS模拟数据和实测数据验证前两部分的计算方法。

1　载波多普勒频移最大（小）值的计算

1.1地心惯性坐标系下的载波多普勒频移最大（小）值计算

1.1.1TSUI对载波多普勒频移最大（小）值的推导

卫星信号的多普勒频移是由用户接收机与卫星在它们两者连线方向上的相对运动引起的。为了分析方便，本文只考虑用户为静止时情况，计算仅由卫星运动所造成的接收信号载波多普勒频移最大值。

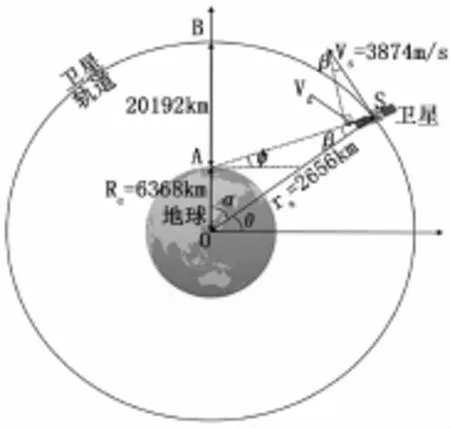
图1　地心惯性坐标系下卫星产生多普勒频移示意图

图1为GNSS卫星产生多普勒频移示意图，图中参数为GPS（global positioning system，GPS）卫星参数。由于地球并非完美的球体，所以并不能用一个值来表达地球的实际半径，但由于地球的形状很接近球体，半径为6 357 km～6 378 km，为了处理方便将这里假设地球为球体，轨道半径为6 368 km。同样，假定卫星轨道为圆轨道，其轨道半径为26 560 km。图中卫星的位置为S，用户的位置为A。由GPS卫星周期为11小时58分，可得卫星的轨道加速度及线速度为：

由于只有相对径向运动才会多普勒频移，卫星相对于用户的速度分量：

vd=vssinβ

下面分析一下该速度分量与卫星角度的关系。对于三角形OAS，利用余弦定理得［3］：

（AS）2=R2e+r2s-2Rerscosα=R2e+r2s-2Rerssinθ

利用正弦定理得：

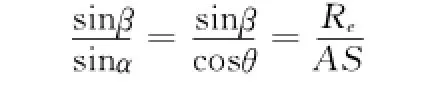
因此：

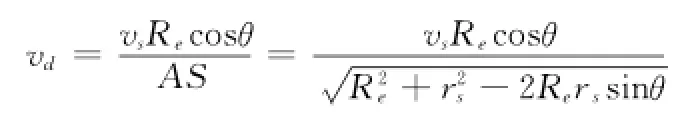
对上式求导得：

当θ=arcsin（Re/rs）时，上式成立。对于GNSS系统用户，更关心的是卫星与用户相对于地平线角度（仰角）大小。

下面，推导角度θ与仰角φ的关系，对三角形OAS应用正弦定理得［3］：

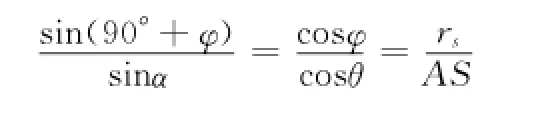
可得：

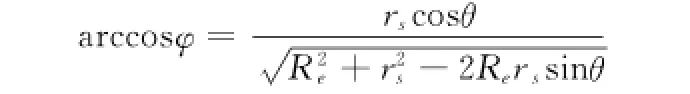
多普勒频移fd与相对速度vd的关系为：

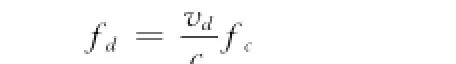
式中，fc为GNSS信号的载波中心频率，c为光速。

所以可以得到多普勒频移fd与仰角φ之间的关系。当卫星速度vs=3 874 m/s时，可得：

当θ=90°时，φ=90°，即卫星位于用户天顶方向，带入式（6）可得vd=0，由式（10）得多普勒频移为fd=0，即天顶方向的多普勒频移的绝对值最小。

当θ=arcsin（Re/rs）=0.242 rad，φ=0°，即卫星与用户的仰角为0°时vdmax=928.82 m/s，对于GPS L1（载波频率为1 575.42 M Hz）的信号：

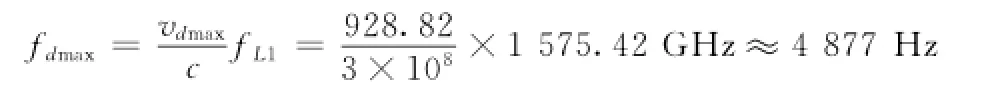
当卫星相对于用户的水平面上升时fdmax=4 877 Hz，当

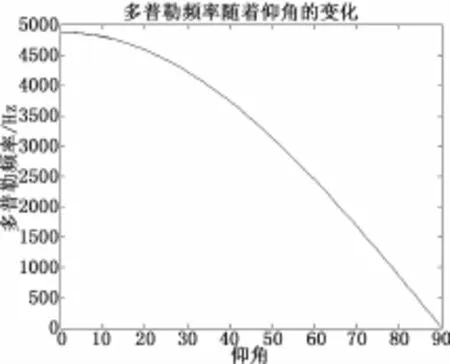
图2　地心惯性坐标系下载波多普勒频移最大值随仰角的变化

卫星相对于用户的水平面下降时fdmin=-4 877 Hz。

vdmax=929 m/s，约为3 344 km/h，这个速度与非常高速的军用航空器相当，因此对于地面一般用户，其动态引起的多普勒频移相当小。

1.1.2卫星高度对载波多普勒频移最大（小）值的影响

以上分析中假定卫星轨道为圆轨道，然而真实情况下卫星在其轨道平面上的轨道方程为

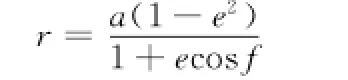
其中：a为长半轴，e为偏心率。

近地点，远地点的轨道高度分别是最小和最大的卫星高度

rmin=a（1-e）

rmax=a（1+e）

一般，GPS卫星轨道的参数值为a=26 560 km，e= 0.006 739 496 742 28，则可以得到

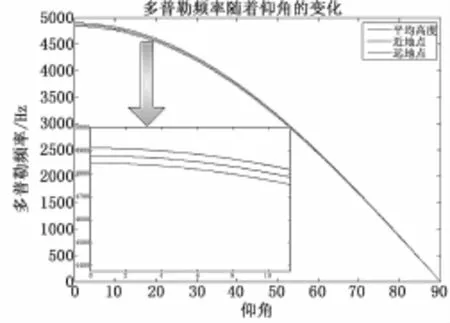
图3　地心惯性坐标系下卫星高度对载波多普勒频移最大值的影响

仰角越小，卫星轨道高度对多普勒频移的影响越大。仰角为0度时，近地点和远地点的多普勒频移相差66 Hz左右，即偏心率每增加0.000 1，多普勒增加1 Hz。所以由于卫星轨道偏心率引起的卫星高度变化带来的多普勒较小，可以忽略不计。

1.2地心地固坐标系下的任意用户位置载波多普勒频移最大（小）值计算

上节中的卫星速度是在地心惯性坐标系下的卫星速度，然而由于地球自转，卫星相对于用户的速度并不是之前的速度，地球自转会对地球上静止的用户带来附加的多普勒频移。因此需要关注的是在地心地固坐标系下的多普勒频移最大值。

为了分析特定用户位置处地心地固坐标系下的多普勒频移最大值，可分为以下几步：

（1）分析地心地固坐标系下的卫星速度大小；c

（2）求解任意用户位置取得多普勒频移最大 （小）值时的卫星位置；

（3）求解地心地固坐标系系下的卫星径向速度，从而计算任意用户位置多普勒频移最大（小）值。

1.2.1地心地固坐标系下的卫星速度

卫星轨道倾斜角度为i，地球自转角速度为ωE，地心惯性下的卫星速度为v→E，地心地固坐标系下的卫星速度为v→F，卫星所对应的纬度为φ，则

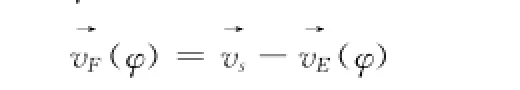
得到通［4］：

则可以

|vF（φ）|2=|vs|2+rs2ωE2cos2φ-2rsωE|vs|cos i

当卫星处于0≤φ≤i时，|vF（i）|≤|vF（φ）|≤|vF（0）|，即|vF（φ）|max=|vF（0）|。GPS卫星轨道倾角i=55°，则|vF（φ）|max=|vF（0）|=3 186（m/s）。

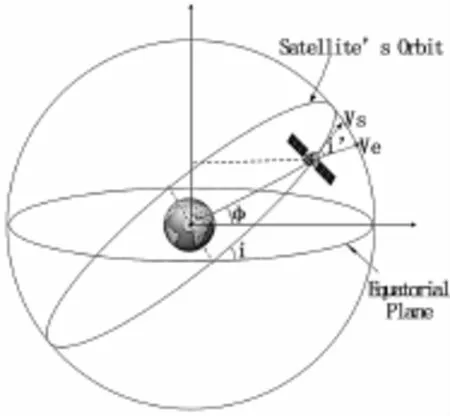
图4　地心地固坐标系下卫星产生多普勒频移示意图

图5　卫星在地心地固坐标系下的速度变化

1.2.2求解任意用户位置取得多普勒频移最大（小）值时的卫星位置

卫星在仰角为0时取得多普勒频移最大（小）值，所以求解卫星取得多普勒频移最大（小）值时的位置，即为求解卫星取得零仰角时的位置。

假设用户位置（B0，L0，H0）（也可表示为（x0，y0，z0）），卫星轨道倾角为i，且已知某颗卫星地心地固坐标下的任一位置（xs，ys，zs），则相对于用户位置的切面与卫星轨道的交点即为卫星取得零仰角的位置（X，Y，Z）。

相对于用户位置的切面方程为

x0·x+y0·y+z0·z=Re2

卫星轨道可以表示为

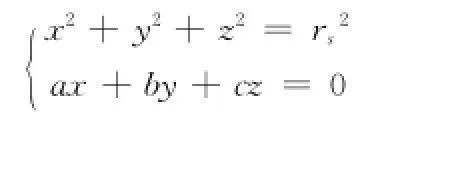
其中 ：iorb→=（a，b，c）是卫星轨道面的法向量；

而iorb→=（a，b，c）可以通过

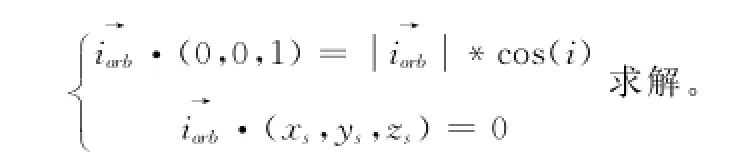
综上，求解取得最大多普勒频移的卫星位置即为（16），（17）方程组的解。

1.2.3地心地固坐标系系下的卫星径向速度

在求得取得多普勒频移最大值的卫星位置（X，Y，Z）（可以转换为（B，L，H））之后，地心地固坐标系下卫星的速度方向向量ivs→=iorb→⊗（X，Y，Z）；而此位置处的地球自转速度方向为ive→=（0，0，1）⊗（X，Y，Z），则卫星在地心地固坐标系（X，Y，Z）处的卫星速度

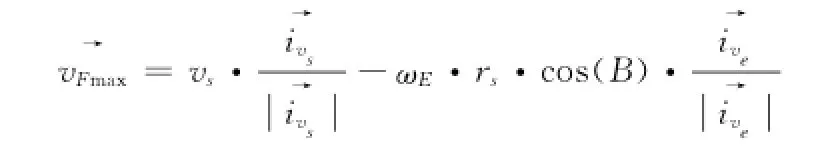
同时用户指向卫星的径向向量为irad→=（X-x0，Y-y0，Z-z0），则卫星在取得多普勒频移最大（小）值位置处的卫星径向速度为vFdmax=vFdmax→·，所以用户（B0，L0，H0）可以取得的多普勒频移最大（小）值为：

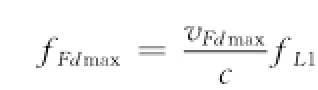
2　基于精密星历的任意用户位置载波多普勒频移计算

上述主要关注的是多普勒频移最大值，接下来要关注的是任意用户位置，任意时刻的多普勒频移。

地心地固坐标系下的用户位置为R→u（经度λ，纬度φ），卫星位置为R→s，则地心地固坐标系下用户指向卫星的矢量为

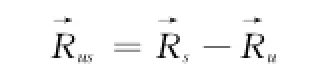
用户位置向东、向北和天顶方向的单位向量如下［5］：

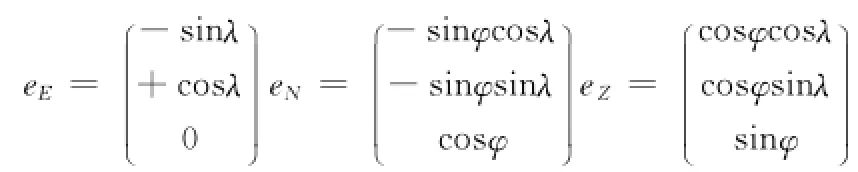
则卫星在东北天坐标系下可以表示为

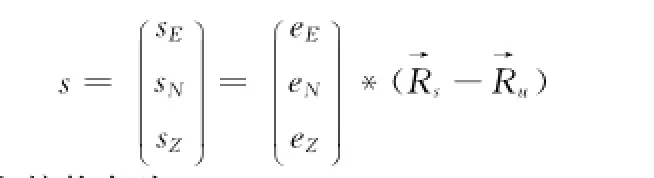
方位角和俯仰角为

当仰角大于0度时，计算此时的多普勒频移。

卫星径向速度为vd=-

综上，在已知用户位置的情况下，可以通过精密星历得到地心地固坐标系下的卫星位置，从而可以得到此时的多普勒频移。

3　实验验证

3.1载波多普勒频移与仰角、方位角之间的关系

在本组试验中，通过GPS模拟器测试2013年3月20日14号卫星于特定点（0°N，116.3°E）的多个时间点的仰角，方位角与载波多普勒频移。则可以得到：

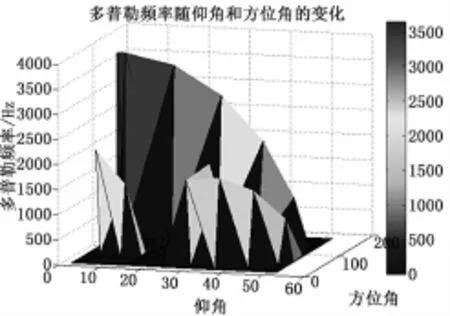
图6　载波多普勒频移与方位角和仰角的关系

通过上图可以看出，在方位角相同的情况下，仰角越小，载波多普勒频移越大；且在仰角为零时，载波多普勒频移取得最大值。

3.2地心地固坐标系下的载波多普勒频移最大（小）值

本节首先验证卫星在不同纬度处的地心地固坐标系下速度，通过GPS模拟器测试2013年3月20日14号卫星的卫星位置和相应的地心地固坐标下卫星速度，则可以得到如图7所示。

图7　地心地固坐标系下不同纬度处的卫星速度

可以看出，实测曲线基本上与理论曲线相符合，差距最大在纬度为0°时卫星速度差在50 m/s。

接着验证任意用户位置处的多普勒频移最大（小）值；主要验证两组：（1）在经度为0°纬度为（0°～90°）处多普勒频移最大（小）值；（2）在纬度为0°经度 （0°～360°）处多普勒频移最大（小）值。

通过以上两组数据的对比，可得出：实测曲线与理论曲线基本符合。即地心地固坐标系下的载波多普勒频移计算方法是正确的。

3.3基于精密星历的任意用户位置载波多普勒频移实验验证

以下四组GPS（L1）数据分别是在北京航空航天大学新主楼F座2楼（20150610，20150624）和11楼（20150721，20150909）采集。11楼的经纬高（39.9790474586°，116.344062256°，98.01183617 m）是接收机长期标定测的，2楼经纬高（39.978886°，116.345618°，56.08 m）是由11楼的经纬高推算得到，则可以仿真得到四组数据的多普勒频移分别如下表1～4所示。

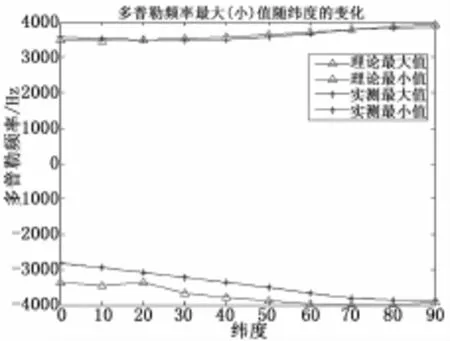
图8　地心地固坐标系下载波多普勒频移最大（小）值随纬度的变化

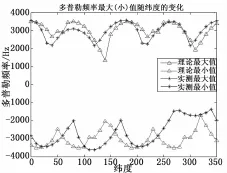
图9　地心地固坐标系下载波多普勒频移最大（小）值随经度的变化

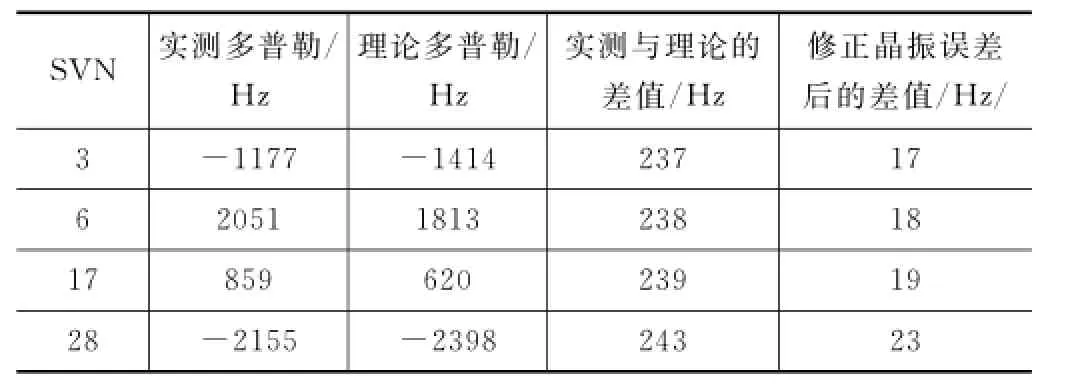
表1　2楼20150610多普勒频移计算

可以看到通过修正晶振误差后，4颗卫星的实测与理论多普勒频移差值在20 Hz左右。

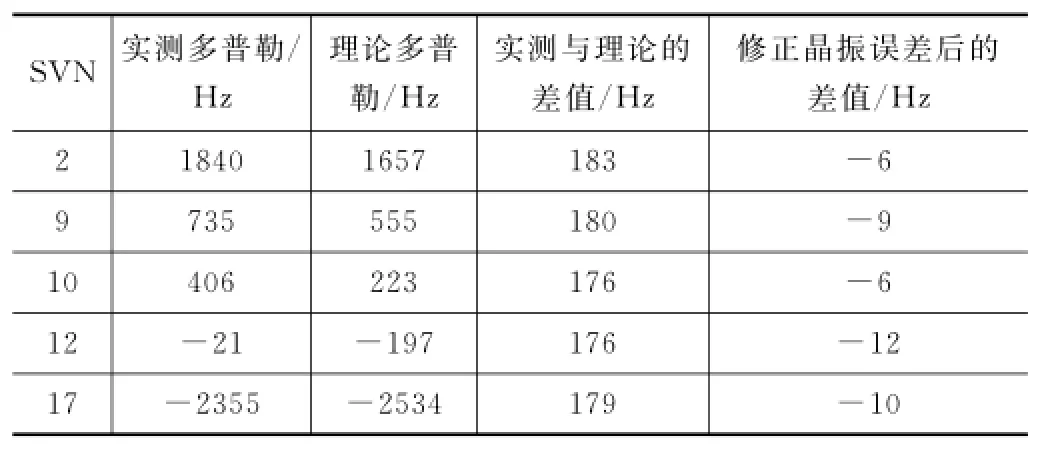
表2　2楼20150624多普勒频移计算

可以看到通过修正晶振误差后，5颗卫星的实测与理论多普勒频移差值在-10 Hz左右。

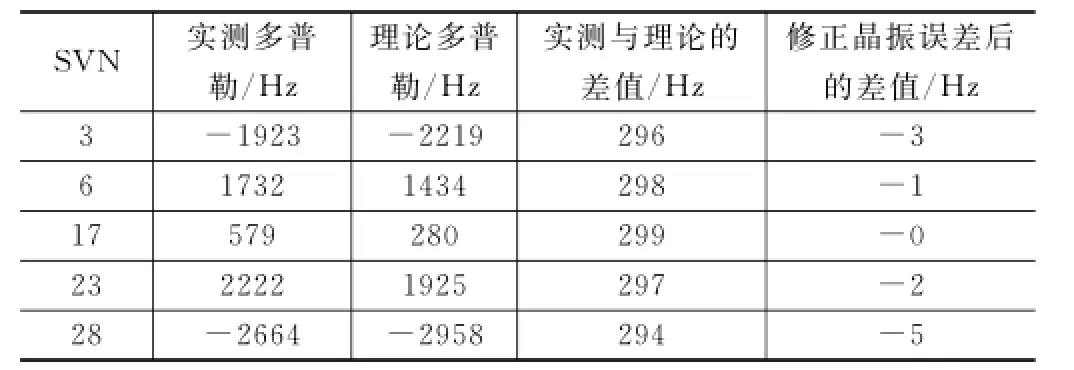
表3　11楼20150721多普勒频移计算

可以看到通过修正晶振误差后，5颗卫星的实测与理论多普勒频移差值在-3 Hz左右。

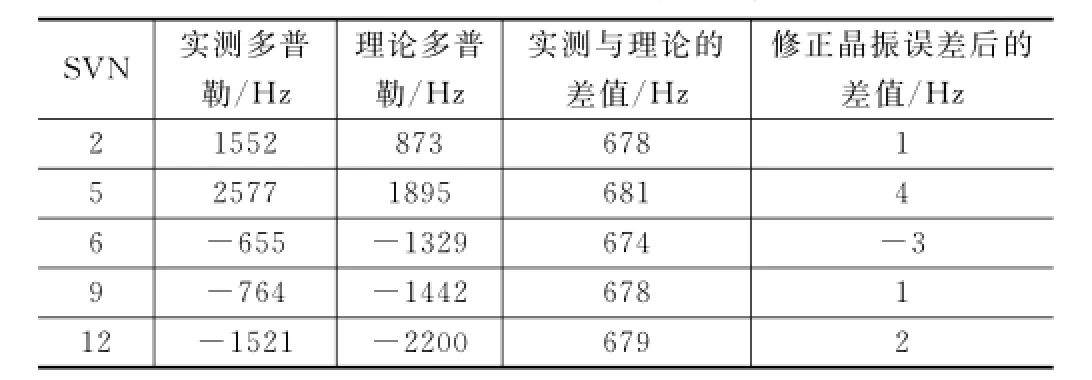
表4　11楼20150909多普勒计算

可以看到通过修正晶振误差后，5颗卫星的实测与理论多普勒频移差值在3 Hz左右。

由以上4组数据的理论计算和实测数据的对比可以得出，任意用户位置的多普勒频移理论计算符合实测数据的多普勒频移。11楼2组数据的多普勒频移误差完全是由晶体振荡误差引起，而2楼2组数据仍存在其他误差来源，可能来源是：（1）2楼位置是由11楼推算出来的，可能存在位置误差；（2）2楼的采集位置处离周围墙壁较近，可能存在多径。

4　结论

本文提出了在地心地固坐标系下任意用户位置载波多普勒频移最大值的精确计算方法，考虑地球自转以及用户位置对多普勒频移的影响，修正了之前TSUI的关于多普勒频移最大值的推导；并且通过实验验证其理论计算曲线基本符合实际测试曲线。

本文同时提出了一种基于精密星历的任意用户位置载波多普勒频移计算方法，可以计算出任意用户位置任意时刻（精密星历时间范围内）的多普勒频移，同时也通过实测数据进行验证，其理论计算值和实测值在修正晶振误差后基本相等（误差在20 Hz以内）。本文提出的载波多普勒频移计算方法在已知精密星历和用户位置情况下则可以计算结果，更易于计算出多普勒频移；并且此计算方法可以得到任意用户位置任意时刻的载波多普勒，在实测数据难以得到时可以代替实测数据计算多普勒频移，所以此计算方法对多普勒频移的理论研究非常有意义。

［1］许晓勇，王飞雪，庄钊文.卫星导航系统信号的多普勒特性分析［J］.国防科技大学学报，2003，25（5）：48－51.

［2］谢钢.GPS原理与接收机设计［M］北京：电子工业出版社，2009.

［3］Tsui J B Y.Fundamentals of global positioning system receivers［M］.Wiley-Interscience，2000：30-40.

［4］Alii I，Al-Dhahir N，Hersheyj E.Doppler characterization for LEO satellites［J］.Communications，IEEE Transactions on，1998，46（3）：309-313.

［5］Montenbruck O，Gill E.Satellite orbits：models，methods and applications［M］.Springer Science&Business Media，2012：36-39.

［6］张爱国，刘梦鑫，陈美连，等.GPS卫星小高度角下多普勒频移的实验分析［J］.厦门理工学院学报，2011，19（1）：30-33.

［7］王克锋，何宇，赵东杰.卫星通信多普勒频移计算方法研究［J］.全球定位系统，2007，31（6）：38-41.

［8］张骞丹，田红心.GPS系统多普勒频移估算的研究［J］.无线电工程，2008，37（4）：21-23.

［9］Amriri S，Mehdipour M.Accurate Doppler frequency shift estimation for any satellite orbit［A］.Recent Advances in Space Technologies，2007.RAST'07.3rd International Conference on［C］. IEEE，2007：602-607.

Calculation，Analysis and Experimental Verification of GNSS Carrier Doppler Frequency Shift

Yang Qian，Qin Honglei
（School of Electronic and Information Engineering，Beihang University，Beijing100191，China）

The Doppler frequency shift is crucial in Global Satellite Navigation System signal processing.This paper studied the calculation of the maximum Doppler frequency shift in Earth-Centered Inertial Coordinate System，its derivation didn't consider the impact of the Earth's rotation rate and user location.This issue was analyzed in this paper，through establishing three-dimensional geometric model of the location and speed between the satellite and the user，proposed a computational method of Doppler frequency maximum shift at any user's location in Earth-Centered Earth-Fixed Coordinate System.Simultaneously，for the calculation of the Doppler frequency shift，proposed a computational method of Doppler frequency shift at any user's location based on the precise ephemeris by constructing the distance vector between the satellite and the user.Finally，GNSSsimulation data and the real data are used to verify，the results of two methods are consistent with the experimental results.Two new methods can compute Doppler frequency shift maximum and Doppler frequency shift at any user' s location in Earth-Centered Earth-Fixed Coordinate System.

GNSS；Doppler frequency shift；ECI；ECEF；maximum

1671-4598（2016）05-0270-04

10.16526/j.cnki.11-4762/tp.2016.05.075

TN967.1

A

2015-11-03；

2015-12-09。

杨茜（1992-），女，陕西咸阳人，硕士研究生，主要从事卫星导航方向的研究。

秦红磊（1975-），男，山东临清人，教授，主要从事卫星导航、组合导航、电子设备的自动测试等方向的研究。