洁净机器人反应转矩观测与碰撞保护研究

宋吉来， 徐　方， 邹风山

（1.中国科学院沈阳自动化研究所，沈阳　110016；2.中国科学院大学，北京　100049；3.沈阳新松机器人自动化股份有限公司，沈阳　110068）

洁净机器人反应转矩观测与碰撞保护研究

宋吉来1，2，3， 徐方1，2，3， 邹风山3

（1.中国科学院沈阳自动化研究所，沈阳110016；2.中国科学院大学，北京100049；3.沈阳新松机器人自动化股份有限公司，沈阳110068）

提出一种基于反应转矩观测器的机器人碰撞保护方法；机器人的反应转矩由基于模型的干扰观测器估值得到，模型的建立包括电机系统转矩模型与机器人系统动力学模型两部分；由于洁净机器人特殊的构型及关节耦合关系，机器人的动力学建模被大大简化，同时对简化后的模型采用最小二乘法对惯性参数和摩擦参数进行辨识，提高了模型的精度；根据永磁同步电机的转矩模型与机器人动力学模型，可以得到基于电机电流的机器人关节转矩；机器人与外界环境接触时，关节转矩的增加量即为反应转矩；通过设计反应转矩观测器并采用力/位混合控制结构，实现基于电流的机器人主动柔顺控制功能，并在洁净机器人进行碰撞保护实验，实际运行结果验证了该方法的有效性。

机器人控制；机器人动力学；碰撞保护；关节转矩控制；系统辨识

0　引言

随着科技的进步与发展，机器人的应用在广度和深度两方面都发生了较大的变革。新一代机器人已不只是工作在安全围栏中，而是能够与人类在工厂、社区、家庭、医院、酒店、银行等开放式场所中协同作业、和谐共生［1］。在这些与人类接触的应用中，安全性已然成为这一领域研究的主要问题。与其相关的研究内容包括人机协同作业、拖曳式示教、力量辅助、碰撞保护等。而在这些应用背后是近年来随着机械、控制、传感三方面技术的进步，迸发出崭新活力的机器人主动柔顺控制这一经典研究问题。洁净机器人是用于半导体制程设备中进行晶圆传输和搬运工作的特种应用机器人［2］。其运行过程中，如果发生碰撞将会损坏机器人自身或晶圆，且影响整个生产线的效率，甚至对工作人员的安全造成损害，因此洁净机器人碰撞保护的研究对于保障机器人自身和环境安全具有重要意义。

根据传感方式的不同，机器人碰撞保护方法分为两大类。第一类采用外部传感器，主要包括外部感知传感器、六维力/力矩传感器和关节转矩传感器等。外部感知传感器常用的有可感知皮肤、接近传感器、视觉传感器等。采用六维力/力矩传感器，灵敏度比较高，但昂贵的价格限制了应用范围。采用关节转矩传感器是近年来兴起的一种新的机器人柔顺控制方式［5］，其对机器人的安全控制是很方便的，但传感器的安装增加了关节的柔性，加大了建模与控制的难度，甚至可能引起振动。第二类为无传感器的碰撞检测方法［6］，通过检查机器人本身具有的编码器、电流等信息来判断碰撞的发生。Kazuhiro Kosuge提出一种基于自适应控制律的碰撞检测方法，其通过自适应控制估计系统模型参数，比较实际力矩与模型给定力矩来判断碰撞的发生［7］。邹风山在研究真空机器人位置误差变化的基础上，采用位置信息，建立基于位置偏差模糊推理的碰撞检测系统，提高了系统碰撞检测的准确性和灵敏度［4］。

机器人与外界环境接触时，由于末端约束力的作用，机器人各个关节上会增加相应的关节转矩，可称之为反应转矩。机器人与外界环境碰撞时，反应转矩会突然增加，因此可以根据反应转矩判断碰撞的发生。本文针对洁净机器人的特点，提出一种采用电流检测式关节转矩传感，直接检测电机电流，利用电机模型与机器人动力学模型，设计反应转矩观测器，对碰撞发生间接测量，实现碰撞保护功能。基于电流的反应转矩检测响应速度快，具有较高的实时性，且不需要额外的传感器，成本低廉，也不会对机器人的结构刚度产生任何影响，具有广泛的适用性。

1　动力学模型

1.1机械结构与连杆参数

洁净机器人工作空间为圆柱形，可实现竖直方向的上下运动，沿竖直轴的旋转运动，以及平面关节三连杆结构用来实现水平方向的伸缩运动。图1是典型SCARA结构的洁净机器人外形图。竖直方向的运动由丝杠传动，水平方向运动由皮带和带轮传动。

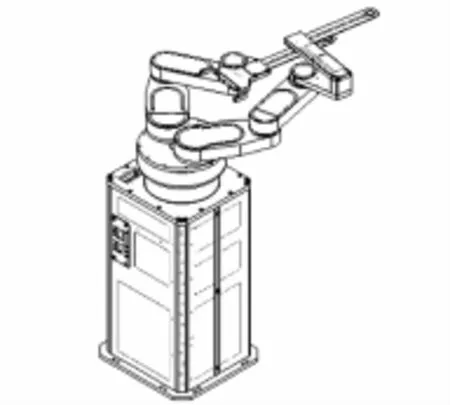
图1　SCARA结构洁净机器人

采用DH法建立洁净机器人的坐标系如图2。

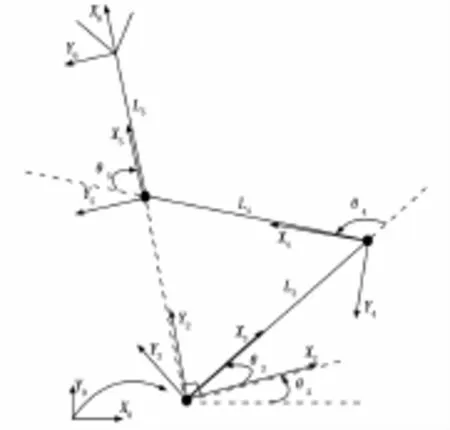
图2　SCARA机器人坐标系

由于SCARA型手臂特殊的结构形式，其角度耦合和连杆长度满足特殊的耦合关系。

角度耦合关系为：

连杆长度关系为：

连杆参数如表1。

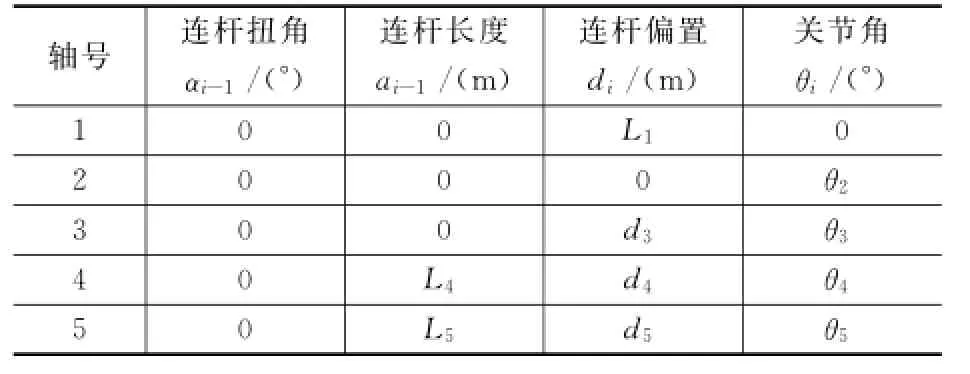
表1　SCARA机器人连杆参数

1.2动力学模型

在不考虑摩擦和环境作用力的情况下，机器人关节空间典型的动力学方程为：

M（q）¨q+C（q，.q）.q+G（q）=τ（3）

其中：q为关节变量。方程的左边各项含义为（n为机器人的关节数也是自由度数）：

M∈Rn×n：关节空间惯性矩阵（对称，正定）；C∈Rn×n：哥氏力和向心力计算矩阵；G∈Rn×1：重力项向量；q∈Rn×1：广义关节偏差向量；τ∈Rn×1：广义驱动转矩向量；

根据机器人动力学的拉格朗日方法，各矩阵和向量可以分别计算得到。

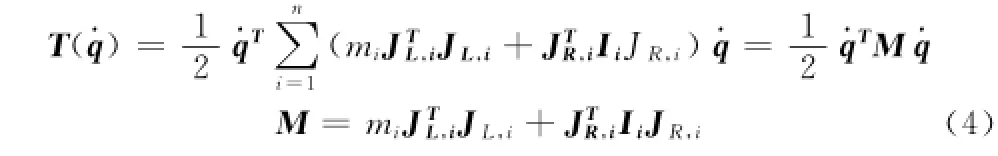
其中：mi为第i个连杆的质量，JL，i和JR，i为连杆i雅可比矩阵的平动项和转动项，Ii为第i个连杆的惯性矩阵。

C矩阵：C矩阵也是由连杆的动能方程导出，其有多种求法，一种特殊的方法为：G向量：重力向量G由势能方程导出。

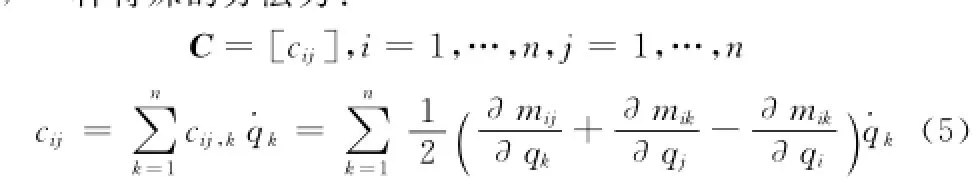
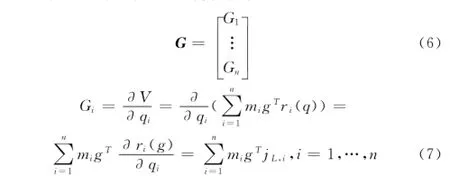
考虑到SCARA结构机器人的特殊构型，整个机器人的旋转运动由2号电机驱动，第3，4，5轴的伸缩运动由3号电机驱动，其水平方向运动的重力项为0。考虑连杆参数和角度的耦合关系，动力学方程可以化简。

1.3动力学参数辨识

考虑摩擦和环境作用力，完整的机器人动力学方程为：M（q）¨q+C（q，.q）.q+Fv.q+Fssgn（.q）+g（q）=τ-JT（q）Fext（8）

其中：Fext为环境作用力，J为机器人的雅可比矩阵。根据动力学方程的性质可以对其化简，并利用系统辨识方法进行参数辨识。

连杆参数的向量形式为：πi=［mimilcixmilciymilciz

I∧ixxI∧ixyI∧ixzI∧iyyI∧iyzI∧izz］T（9）

根据动力学模型的特性，动力学方程可以被线性化为如下形式：

简记为：

τ=Y（q，.q，¨q）π（11）

测量以下变量：

1）直接测量q和.q（采用编码器）；

2）间接测量¨q（构建滤波器）；

3）间接测量τ（基于电机电流）；

得到N次数据：

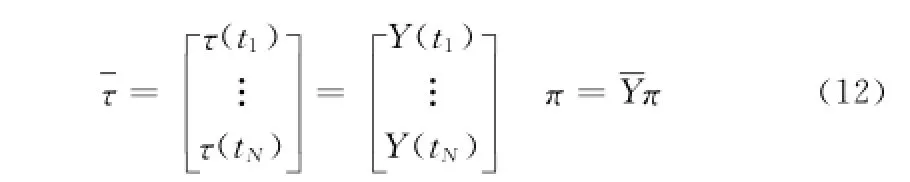
采用最小二乘辨识算法得到辨识结果：

2　反应转矩观测与碰撞保护

2.1电机转矩模型

反应转矩为机器人与外界环境接触时所增加的关节转矩，而关节转矩的检测采用电流式关节转矩传感，因而需要建立交流永磁同步电机的转矩模型。

永磁同步电机模型的建立过程中做以下基本假设［8］：

1）转子永磁磁场在气隙空间分布为正弦波，定子电枢绕组中的感应电势也为正弦波；

2）忽略定子铁心饱和，认为磁路线性，电感参数不变；

3）不计铁心涡流与磁滞等损耗；

4）转子上没有阻尼绕组。

三相永磁电机可以在空间矢量坐标系下分析，有如下矢量方程。

磁链方程：ψs=Lsis+ψf=Lsσis+Lmis+ψf（14）式中，Ls是定子自感，包括漏感Ls和励磁电感Lm两部分，励磁电感Lm=1.5 Lab，Lab是三相坐标系下的两相互感。ψf是转子磁链矢量，ψf=ψfejθe，θe是转子角度，也就是转子磁场定向下的定向电角度。

电压方程：

其中，

转矩方程：电磁转矩表示为磁链和电流的外积，恒幅值变换下表示为：

转子磁场定向以后，转子磁链ψf只有d轴分量，稳态下d轴电流为零。根据式（14）、（15）和（16）分别可得下列方程。

磁链方程：电压方程：转矩方程：

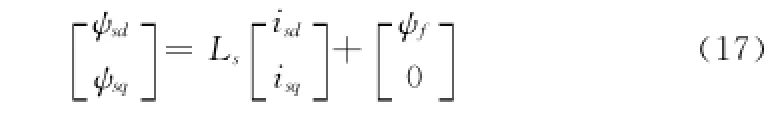
其中：τp称为永磁转矩，τr称为磁阻转矩，对于表贴磁体，Ld=Lq，磁阻转矩为0，从而：

保持磁链幅度不变，通过控制q轴电流可以独立控制电磁转矩。

2.2反应转矩观测器设计

机器人与外界环境作用过程中，反应转矩可以视为负载力矩扰动，这种干扰具有多变性、不确定性和随机性，无法预见和准确测量。而扰动观测器（DOB）不需要建立干扰的准确的数学模型，而且它本身的结构简单，避免了大量的计算，能够良好地满足实时要求。

图3为扰动观测器的基本结构框图。在实际的对模型的构建的过程中，得到的模型总是会与实际系统有某些差别。DOB会把实际系统和名义系统的输出之间的差异作为一种干扰，并将这种干扰输入到原来的模型中。图中，P（s）表示实际控制系统的传函，Pn（s）是名义的数学模型，u代表的是系统的输入，d是影响系统的外部的干扰，^d为d的估算值。

图3　扰动观测器基本结构图

名义模型的逆矩阵P-1n（s）是没有办法进行物理实现的，解决措施是在干扰观测器的两个输入端同时串联一个滤波器Q（s），使得Q（s）的相对阶次能够大于或者等于名义模型的相对阶次，使名义模型成为了物理上可以实现的函数。Q（s）可以选择为一阶低通滤波器。

机器人完整动力学方程 （8）可以改写为反应转矩形式：

M（q）¨q+C（q，.q）.q+F（q，.q）+g（q）=τ-τext（21）式中，F（q，.q）为机器人关节处的摩擦力矩，τext为施加在关节上的外作用力矩，即反应转矩。

减速器传动的机器人，关节角度和转矩满足：

q=N-1qm（22）

τ=Nτm（23）式中，N∈Rn×n是每个关节减速比的对角阵。

考虑电机转子动力学，转子的转矩平衡方程重写为：

Jm¨qm+Fm（qm，.qm）+N-1（M（q）¨q+C（q，.q）.q+

F（q，.q）+g（q）+τext）=τm（24）

式中，Jm为电机转子的惯量，Fm（qm，.qm）为电机转子处的摩擦力矩。带入关节角度关系，得到：

（M（q）+N2Jm）¨q+C（q，.q）.q+F（q，.q）+g（q）+τext=τ（25）

推导过程中，将电机转子处的摩擦归入摩擦项F（q，.q）。式（25）为计及电机转子动力学在内的机器人完整动力学模型。

由此可得作用在关节上的反应转矩τext：

τext=τ- ［（M（q）+N2Jm）¨q+C（q，.q）.q+ F（q，.q）+g（q）］（26）

加入一阶低通滤波器，代入电机转矩模型和关节转矩传递关系，得到：

实际工程之后，式（27）中一些项的参数不能精确获得或者本身的模型不够精确，因此只能用相应项的估计值代替，由此得到最终的反应转矩观测器为：

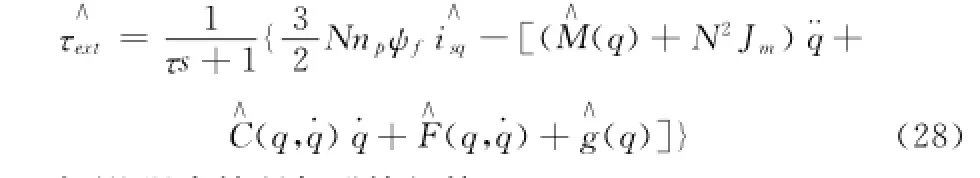
2.3力/位混合控制与碰撞保护

力/位混合控制基于机器人位置子空间与力子空间的互补性、正交性，在位置子空间进行位置控制，在力子空间进行力控制。Raibert和Craig于1981年提出了力/位混合控制［9］。基于反应转矩观测器的机器人力/位混合控制结构如图4所示，该控制结构可用于碰撞保护、拖曳式示教等多种力控制应用。图中τext被视为扰动量，τ、qd为系统输入，q为系统输出，τe∧xt为的估值，当反应转矩观测器的输出∧超出一定阈值，则判τextτext断碰撞发生。关节转矩的传感采用电机电流和系统模型。每个关节既有位置控制器，又有力控制器。为了根据约束条件改变每个自由度所要求的控制模式，图中引入了选择矩阵S和S′，其为3×3矩阵，是两组互锁开关。如要求第i个关节进行位置（或力）控制则矩阵S（或S′）对角线上的第i个元素为1，否则为零。

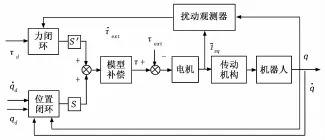
图4　基于反应转矩观测器的力/位混合控制结构图

3　实验

洁净机器人连杆结构对称，惯性矩阵的主要项为Ixx，Iyy和Izz，其他项的值比较小可以被忽略。通过矩阵相乘，Ixx和Iyy项也被消掉，动力学计算值仅与Izz项相关。通过最小二乘法参数辨识可以得到每个连杆的Izz项，如表2所示。

机器人的摩擦辨识通过测量匀速运动过程中的关节转矩，并减去动力学所引起的转矩项得到。摩擦辨识结果如表3所示。

表2　机器人连杆惯性参数Izz

表3　机器人连杆惯性参数Izz

图5为机器人在碰撞保护功能使能和禁止情况下发生碰撞时的电机转矩曲线。在碰撞发生后，第一个任务是快速而准确的判断出碰撞的发生，判断出系统发生碰撞后的一个重要问题是如何控制机器人，保证将碰撞造成的伤害降到最低。本文采用驱动器动力下电的方式，使用软件输出为驱动器下动力电或切断驱动器动力电源。如图5中曲线所示，机器人发生碰撞后，通过反映转矩判断碰撞发生，并下动力电，电机电流迅速将为0值。该方法可以有效的保护机器人自身和外部环境的安全。

图5　碰撞过程电机转矩曲线图

4　结论

本文提出一种基于反应观测器的机器人的碰撞检测方法，该方法不需要使用额外的传感器，仅根据电机电流以及系统模型来进行碰撞检测。系统模型包括电机转矩模型和机器人动力学模型两部分，在机器人模型化简后采用最小二乘法进行系统参数辨识，提高系统的准确性与灵敏度。同时通过设计反应转矩观测器和力/位混合控制结构，实现机器人的主动柔顺控制功能。最后针对洁净机器人进行碰撞保护实验，实验结果表明该方法可以在非常短的时间内判断出碰撞的发生，采取有效地措施，保障机器人与外界环境的安全。

［1］Yamada Y，Hirasawa Y，Huand S，et al.Fail-safe human/robot contact in the safety space［A］.International Workshop on Robot and Human Communication［C］.IEEE，1996：59-64.

［2］丛明，沈宝宏，于旭.面向IC制造的净化机器人［J］.高技术通讯，2007，17（4）：395-400.

［3］梁燕华，金鸿章.模糊控制策略在避碰运动系统中的应用［J］.系统仿真学报，2008，20（6）：1554-1558.

［4］邹风山，曲道奎，徐方，等.基于位置误差的真空机器人碰撞保护研究［J］.组合机床与自动化加工技术，2009，9（9）：17 23.

［5］Spong M W.Modeling and control of elastic joint robots［J］.Journal of Dynamics Systems，Measurement and Control，Transactions of the ASME，1987，109（4）：310-319.

［6］De Luca A，Ferrajoli L.Exploiting Robot Redundancy in Collision Detection and Reaction［A］.2008 IEEE International Conference on Intelligent Robots and Systems［C］.2008：3299-3305.

［7］Morinaga S，Kosuge K.Collision detection system for manipulator based on adaptive impedance control law［A］.IEEE International Conference on Robotics and Automation［C］.Taipei，ROC，2003：1080-1085.

［8］Pillay P，Krishnan R.Modeling，Simulation，and Analysis of Permanent-magnet Motor Drives，Part I：The Permanent-magnet Synchronous Motor Drive［J］.IEEE Transactions on Induced Application.1989，25（2）：265-273.

［9］Raibert M H，Craig J J.Hybrid Position/Force Control of Manipulators［J］.Transactions of ASME Journal of Dynamics Systems，Measurement，and Control.1981，102：126-133.

Reactive Torque Observation and Collision Protection for Clean-room Manipulator

Song Jilai1，2，3，Xu Fang1，2，3，Zou Fengshan3
（1.Shenyang Institute of Automation，Chinese Academy of Sciences，Shenyang110016，China；2.University of Chinese Academy of Sciences，Beijing110049，China；3.SIASUN Robot& Automation Co，Ltd Shenyang，Shenyang110068，China）

An approach of robot collision protection based on reactive torque observation is presented.Reactive torque is estimated by the disturbance observer based on the model of the system，which including motor torque model and robot dynamic model.Because of the special structure and joint coupling relationship of clean-room robot，the dynamics of robot is greatly simplified，and simplified model is identified by the least squares method which improved the precision of the model.According to the torque of permanent magnet synchronous motor and dynamic of the robot，joint torque based on motor current can be getted.When robot contact with the external environment，the increasion of the joint torque is the reaction torque，which is used to implement the active compliance control combined with disturbance observer and the force/position hybrid control.At last，collision protection experiment is carried out on the clean-room robot，and the experimental results verify the effectiveness of the proposed method.

robot control；robot dynamics；collision protection；joint torque control；system identification

1671-4598（2016）05-0246-05

10.16526/j.cnki.11-4762/tp.2016.05.069

TP273

A

2016-02-22；

2016-03-23。

国家科技重大专项（2014ZX02103005）。

宋吉来（1982-），男，辽宁营口人，博士研究生，主要从事机器人控制方向的研究。