“六西格玛”方法在机载测试参数误差分析中的应用

朱　攀，尹　川，王　锦

（中国飞行试验研究院，西安　710089）

“六西格玛”方法在机载测试参数误差分析中的应用

朱攀，尹川，王锦

（中国飞行试验研究院，西安710089）

科研试飞中，为真实反映飞机各项技术指标的实际状态，机载测试系统需提供精确的数据，而测试的中间环节较多，所测的各种参数结果势必会有误差；为满足试飞任务的精确需求，本文通过从测试系统误差的来源入手，来分析机载测试参数产生误差的各个环节，以压力参数为例，运用“六西格玛”方法中的测量参数误差的定义、测量、分析、改进及控制五项流程，以三架机的压力传感器的校准历史数据为样本，对精度结果作了详细分析，得出了事先确认参数具体压力变化区间，根据测试系统精度分布特点选用更合适范围的传感器来保证精度要求，将6西格玛”方法用于压力参数误差分析可行的结论；并提出，将其推广到其它各类测试参数的误差分析，将有利于在现有条件下更合理地配套测试仪器设备，更好地满足参数测试精度需求。

机载测试系统；误差；六西格玛

0　引言

一切科研试飞都是试验数据为基础，而精确的数据才能真实反映飞机各项技术指标的实际状态，为飞机定型提供重要依据。机载测试系统是获取飞机试验数据的前端，是决定数据好坏的关键所在，如何保证所搭建的测试系统测得参数的误差能满足任务的精度需求是一项势在必行的工作。

1　引起机载测试参数误差的因素

一个待装机的传感器都必须进行装机前的校准，所得到的校准报告将作为飞行试验数据处理的基准。其校准过程可用图1所示的框图表示，即由标准器施加标准信号给被校传感器，被校传感器的输出进入数据采集器进行数据采集及校线处理，生成的校线提供给数据处理使用，完成这些实验室工作后进行设备装机。

从图1中可以看出，在整个链路中包括以下误差环节：

1）标准器自身误差；

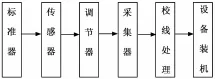
图1　传感器校准及装机链路示意图

2）传感器自身误差；

3）被校传感器在标准器上的连接方式误差；

4）数据采集与处理设备的误差；

5）机上安装误差；

6）电气连接误差。

机上安装误差可以归结为系统误差，如过载角速度组合传感器的安装面不是水平的，会引起零位的偏移，通过飞机架水平后调平安装面能消除偏移，压力传感器的测压管路本身会造成压力损失，通过理论计算或试验的方法能得出对应管径单位长度的压力损失，再对所测压力予以修正。

电气连接误差主要来自人为因素，主要因接线不当引起。如：测单端信号时，信号地要求与采集器ADC/012/10V模块的内部地短接，若不短接会造成采集模块本身的非线性输出，使模块的精度降低，如图2所示。

2　精度及误差的关系

精度可分为精密度、准确度、精确度。

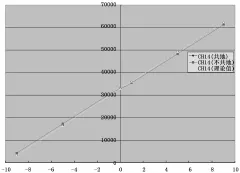
图2　ADC/012/10V模块的输出线性

精度又称精确度，用来描述测量结果与真值的接近程度，是测量结果中系统误差与随机误差的综合，即精密准确程度。只有当系统误差和随机误差都小时才能成为精度高，图3（a）所示。

准确度用来描述测量结果中系统误差的大小程度，即在一定条件下，测量中所有系统误差的综合。测量中系统误差越大，则被测量的测量结果对其真值的偏离越大，测量结果的准确度越低，图3（b）所示。

精密度用来描述测量结果中随机误差的大小程度，即在一定条件下进行多次重复测量时，各测量值之间的接近程度。随机误差越大，数据越分散，测量值的精密度越低，图3（c）所示。

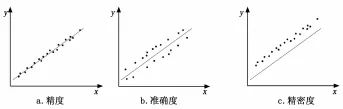
图3　精度等示意图

3　用“6西格玛”方法分析压力参数的误差

西格玛原文为希腊字母sigma，其含义为“标准偏差”，6西格玛意为“6倍标准差”，在质量上表示每百万坏品率少于3.4，图4为不同西格玛水值对应的出错率。6西格玛模式的含义并不简单地指上述这些内容，而是一整套系统的理论和实践方法，是一项以数据为基础追求几乎完美的质量管理方法。6西格玛管理方法重点是将所有的工作作为一种流程，采用量化的方法分析流程中影响质量的因素，找出关键的因素加以改进从而达到更高的客户满意度。

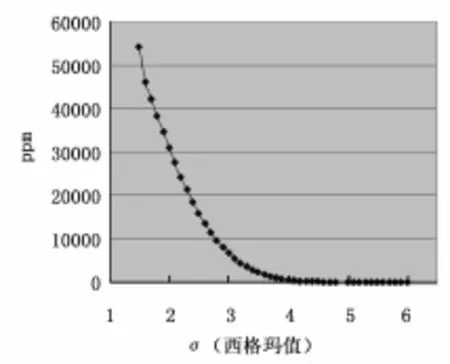
图4　不同σ值对应出错率

用6西格玛方法分析测试参数误差，其典型西格玛水平对应的出错率及出错时间间隔如表1所示，其工作流程如图5所示。

表1　典型西格玛水平出错率及出错时间间隔

1）当δlim≥3σ时，P｛x0-x0·1%≤x≤x0+x0·1%｝≥99.73%考虑到实际情况下分布曲线中心线会偏移，实际只能达到P≥93.3%；

2）当δlim≥6σ时，实际只能达到P≥99.999 66%。

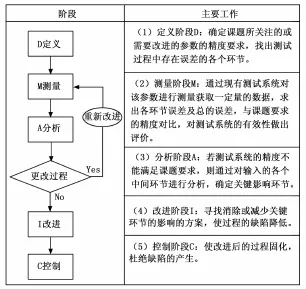
图5　6用西格玛方法分析测试参数误差的流程

3.1定义阶段

课题任务书提出的压力参数精度为0.5%，是指测得值的极限误差相对于真值的百分比，假设真值为x0，极限误差δlim=x0·0.5%。引起误差的环节很多：

1）标准器自身误差；

2）传感器自身误差；

3）被校传感器在标准器上的连接方式误差；

4）数据采集与处理设备的误差；

5）机上安装误差；

6）电气连接误差。

在试验室环节通过对传感器及采集器等设备的联校基本消除了系统误差；在压力传感器装机后带来的误差主要是系统误差，通过严格控制管路长度、计算修正可以基本消除；电气连接误差主要由共地问题引起的非线性误差，确保正确共地后，误差基本消除；但各环节中随机误差由很多不确定因素造成是无法消除的；对于压力参数，误差分析的重点在传感器、调节器、采集器本身及联校环节的随机误差。

因此将传感器单独输入输出、采集器单独输入输出、联校时的输入输出作为实验考虑的环节，根据得到实验数据，用统计学方法算出各环节输出相对误差的标准差σ1、σ2、σ。

3.2测量阶段

对三架机的168个压力传感器的校准历史数据为样本进行分析，输入和输出是线性关系，校线是经多次测量回归出的一条直线，以直线上的点为理想值，以校准记录的各点为实际值，求出各环节每个点的实际相对误差及FSR误差，如图6所示。

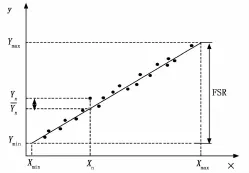
图6　实际相对误差及FSR误差

1）实际相对误差：

（实际值-理想值）/理想值，得到每个点的相对误差，共1 107个点，以这1 107个点的相对误差为样本，样本用An（n =1，2，…，1 107）表示，

An=，反复测量的各点的相对误差为随机误差，A～N（0，σ2），按概率论和数理统计方法，在一定置信概率下随机误差的极限值δlim作为测量列每一测得值的随机误差。

Yn）为每个校准点的坐标，对于每个传感器的校线y=ajx+bj，aj、bj值通过该传感器的校准点回归得出。

将1 107个点所对应的Xn，Yn，aj、bj值分别代入求出An

通过贝塞尔公式计算：

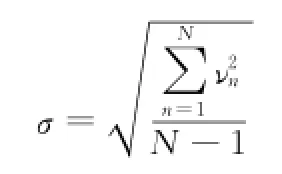
式中，N：1 107；νn为残余误差，νn=An

计算得到：

σ1=0.23%，σ2=0.1%

σ=0.202%，3σ=0.606%，6σ=1.21%

2）FSR误差：

几乎所有传感器及设备都给出了满量程精度这一指标来表示它的精度等级（如0.5%F.S），它是指传感器或设备静态校准曲线与拟和直线间的最大偏差Ymax与满量程输出比的百分数。

（实际值-理想值）/FSR，得到每个点的相对误差，共1 107个点，以这1 107个点的相对误差为样本，样本用Bn（n =1，2，…，1 107）表示，Bn=Yn/FSR，FSR=Ymax-Ymin，反复测量的各点的相对误差为随机误差，B～N（x0，σ2），按概率论和数理统计方法，在一定置信概率下随机误差的极限值δlim作为测量列中每一测得值的随机误差。FSR

（Xn，Yn）为每个校准点的坐标，对于每个传感器的校线y=ajx+bj，aj、bj值通过该传感器的校准点回归得出。

将1 107个点所对应的Xn，Yn，aj、bj值分别代入求出B n

通过贝塞尔公式计算：式中，N：1107，νn为残余误差，νn=Bn

计算得到：

σ1=0.055%，σ2=0.05%，

σ=0.052%，3σ=0.156%，6σ=0.312%

3.3分析阶段

通过计算得到了两种精度结果，如表2所示，将得到的两种精度结果进行对比

1）分析方法的不同导致了结果差别较大。

（1）FSR精度是各测点的绝对误差相对于满量程的比值，FSR精度容易保证。通过“六西格玛”方法得到压力参数的FSR精度为0.31%，小于0.5%，满足课题FSR精度要求。

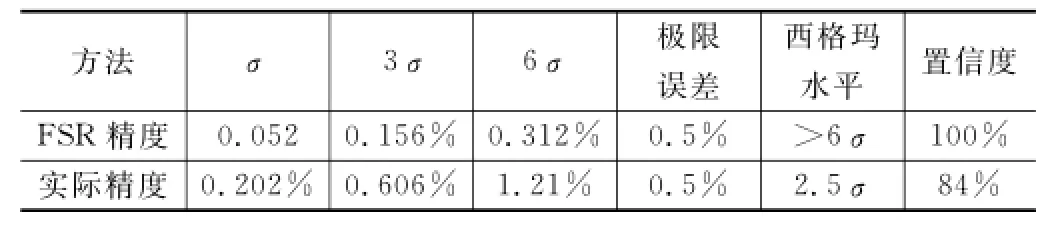
表2　计算得到的两种精度结果

（2）实际精度是各测点的绝对误差相对于该点真值的比值，在小量程范围的精度不易保证。只使用传感器后84%的量程能满足0.5%精度要求。

2.从实际精度的数据可以看出：

（1）从精度要求为0.5%，而置信度只能达到84%来分析，原因为传感器信号区间有16%是达不到0.5%精度要求的，可以理解为传感器量程的前16%区域相对误差可能会超出0.5%。

（2）从精度要求为1.21%，而置信度能达到100%来分析，可以理解为传感器在整个量程区间的实际精度为1.21%。

（3）如果要求实际精度，压力参数的精度在传感器量程后84%的区间能满足0.5%精度要求，而在前16%区域精度处于0.5%～1.21%之间。

3.4改进及控制阶段

1）提高传感器及采集器小量程范围的精度。这个很难做到，代价太高。

2）事先确认参数具体压力变化区间，根据测试系统精度分布特点选用更合适范围的传感器来保证精度要求。

4　结论

1）将 “6西格玛”方法 （DMAIC）用于测试参数的误差分析，取得较好的效果，说明“6西格玛”方法用于参数误差分析是可行的，能推广到其它各类参数的误差分析。

2）通过“6西格玛”方法分析测试系统误差，利于在现有条件下更合理配套测试仪器，更好大满足参数测试精度需求。

［1］任岫云.精益六西格玛项目管理模式研究及系统开发［J］.现代管理技术，2011，38（1）：40-46.

［2］胡鸿志.基于电源电流和输出电压的模拟电路故障模型研究［J］.计算机测量与控制，2015，23（7）：2266-2269.

［3］姚明源.差压式流量计的误差分析及处理［J］.仪表技术，2012，2：48-50.

［4］于丽杰.MEMS传感器随机误差分析［J］.传感器与微系统，2012，31（3）：63-65.

［5］宋凝芳.光纤陀螺随机误差特性的小波方差分析［J］.红外与激光工程，2010，39（5）：924-928.

Analysis of Parameter Error in Flight Test by 6 Sigma Methods

Zhu Pan，Yin Chuan，Wang Jin
（Chinese Flight Test Establishment，Xi'an710089，China）

In flight test，in ordor to reflect actual status of technical parameters，flight test system must provide accurate data，including many processes，flight test system'parameters must exist error.To meet the precision requirements，this text analyzed the possible processes that bring error，illustrated by the example of pressure parameter，starting with the method of"six Sigma"definition，measurement，analysis，improvement and control of the five processes，with three airplane's pressure sensor calibration original data as samples，analyzed precision results，and educed that in advance to confirm specific pressure change interval parameters，according to the distribution characteristics of the test system precision to choose appropriate sensors to meet precision requirements，analysis of pressure parameter error in flight test by 6 Sigma methods is possible.Finally educed conclusion that generalized to other test parameters error analysis can lead us match the instruments rationally and meet the precision requirements.

flight test system；error；6 Sigma

16714598（2016）05018303

10.16526/j.cnki.11-4762/tp.2016.05.052

TP3

A

2015-10-27；

2015-12-27。

朱攀（1980-），男，硕士，工程师，主要从事飞行试验、测试系统方向的研究。

尹川（1987-），男，硕士，助理工程师，主要从事飞行试验、测试系统方向的研究。