面向低强度无线网络信号接收谱参数估计研究

李　瑾，戴春燕，洪　阳

（1.包头钢铁职业技术学院自动化系，内蒙古包头　014010；2.内蒙古科技大学信息工程学院，内蒙古包头　014010）

面向低强度无线网络信号接收谱参数估计研究

李瑾1，2，戴春燕1，洪阳1

（1.包头钢铁职业技术学院自动化系，内蒙古包头014010；2.内蒙古科技大学信息工程学院，内蒙古包头014010）

针对以北斗卫星导航信号为代表的亚纳秒级的低强度无线网络信号在定位中难以获取精确时间估计及角度估计，且易受环境噪声影响，使其定位精度不高等难题，提出了基于亚纳秒级的低强度无线网络信号接收谱参数估计方法；首先通过抽样方式，将发射信号抽样为多维独立子信号并独立建模，通过构造噪声空间与子信号空间在对应列向量正交化的基础上精确获取TOA估计；随后利用复数域映射，在获取TOA估计基础上采取比对方式精确地获取DOA估计；最后对所提参数估计方法进行了精度分析；测试数据显示：与PM算法、ESPRIT算法相比，所提技术在TOA及DOA估计上更为精确；同时在信号强度低且背景噪声干扰严重的情况下，所提方法仍可有效的维持参数估计精度；该技术能够有效减轻背景噪声对信号传输的影响，具有较强的实际部署意义。

无线网络；信号接收谱；DOA估计；TOA估计；复数映射

0　引言

在低强度天地无线信号定位过程中，信号的时达估计（TOA估计）的准确获取，以及信号波达估计（DOA估计）的方向获取，成为影响卫星定位精确度最为重要的两个参数［1-3］。ROVNAKOVA J［4］提出可以基于信号接收强度检测并结合信号相干检测的方式，来实现TOA估计。但是当卫星和地面处于非同步状态时，随着卫星轨道半径的扩大，其TOA估计性能将迅速的下降。MARZETTA［5］提出为了改善信号的TOA估计，首先采用PM算法将TOA估计中的信道进行单位冲激响应，然后在此基础上对谱密度采用范数估计等方式实现频域内的峰值曲线搜索，随后根据峰值曲线进行反变换，从而获取到良好的TOA估计。然而由于该技术对频域要求极高，一旦出现多普勒频移，特别是多普勒频移处于不断变动状态时，它将很难在频域内对TOA进行估计，估计精度也大大下降。LARSSON［6］提出了基于波函数空间递归的方式，采用ESPRIT算法将TOA的频域映射为不变小波函数，通过对不变小波函数进行自递归获取TOA峰值，在信号变换频繁时能够实现精确定位。但是，由于专门针对时变节点进行定位，导致当节点处于固定状态的时候，其难以做到对TOA峰值进行自递归，从而降低了定位的精确度。

为了解决上述难题，本文提出了一种新的接收谱参数估计机制。首先对接收到的信号进行抽样，以获得多路互相独立的子信号。同时为改善抗噪性能，根据子信号在接收过程中的特性，基于特征值和特征向量，将信号空间分割为互相独立的信号子空间和噪声子空间，实现了将信号和噪声的正交化精确分离，减少了噪声对定位精确程度的影响。同时根据信号子空间和噪声子空间互相正交的特性进行复数域映射，准确计算出TOA和DOA估计；并将TOA及DOA估计问题演变为在复数域上求零点的问题，在复数域上实现了精度的准确求取和误差控制；最后对本文方法进行了仿真分析。

1　信号模型

假设基于亚纳秒级的低强度无线网络信号通过天基平台进行发射，其发射时基带信号采用十六进制频移键控调制（16FSK调制），信号在调制过后分为M个子信号进行传输，每路子信号分为λ个信号传输路径。则其单位冲激响应H（k）（ω）为：其中：ε（ω）为单位阶跃响应，βl（M）为第M个子信号在第l个传输路径上的频域信号衰落，ωl表示该路频域信号的频率延迟。

依据模型（1），则地面设备接收到第M个子信号的数学表达式可写为如下的形式：Y（M）（ω）=N（M）（ω）+S（ω）H（k）（ω）（2）

其中：Y（M）（ω）为该路信号的频率表达；N（M）（ω）为该路信道中的高斯白噪声干扰，均值为1，标准差为0；S（ω）为发射信号，其时域信号表达式s（t）由如下的模型决定：

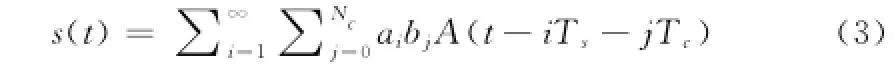
其中：Ts表示脉冲信号的符号周期；Tc表示脉冲信号的发射周期；Nc表示信号中的脉冲符号在Tc内的最大出现次数；bj为调制过程中的伪随机序列，且满足bj∈｛+1，-1｝；ai为调制的脉冲符号序列，且满足ai∈｛+1，-1｝。

此外，式（3）中的各个参数还满足如下的表达式：A（t）=e（1-4πt2/Λ2）（-2πt2/Λ2）（4）

其中：Λ为信号脉冲的阶跃响应

依据上述模型，将模型（2）演变为：

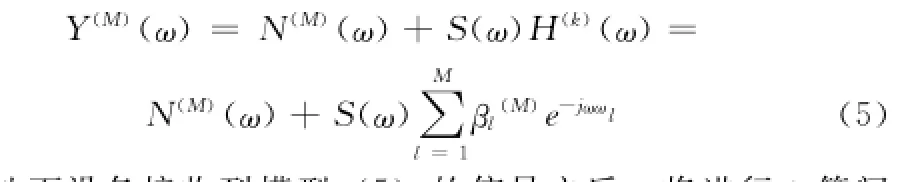
当地面设备接收到模型（5）的信号之后，将进行λ等间隔抽样过程，其采样频率Δω满足：Δω=2π/λ（6）模型（5）经过λ等间隔抽样过程之后得到的采样信号为：

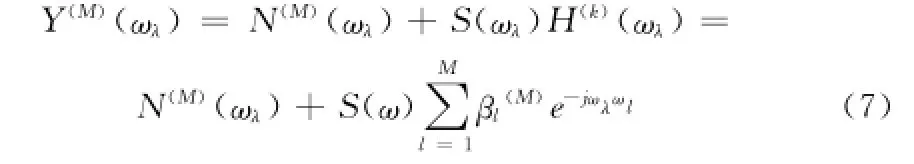
其中：ωλ=λΔω。

为了便于计算，将模型（7）简化为矢量矩阵：

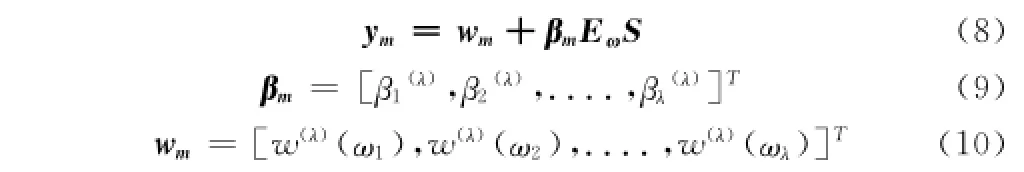
ym=［Y（M）（ω1），Y（M）（ω2），........，Y（M）（ωλ）］T为接收信号的λ等间隔抽样后得到的采样信号；βm代表任意第M路子信号的衰落矢量；wm为高斯白噪声进过λ等间隔抽样后得到的采样信号；S=Λ［S（ω1），S（ω2），......，S（ωλ）］T为秩值λ的对角矩阵，对角线上元素为S（ω）进行了λ等间隔抽样后得到采样值；Eω为单位时延矩阵，Eω=［E1，E2，....，Ei］，其中Ei满足：

Ei=［1，e-jΔωωi，e-2jΔωωi，.....，e-λjΔωωi］T（11）

2　本文信号接收谱参数估计

2.1信号的接收与接收谱函数的构造

由于定位信号的数据源为天基平台，如典型的北斗卫星轨道高度为3.6万千米，而接收设备的天线距离与卫星轨道高度相比可以忽略不计，因此各路子信号射入的方向是平行的。

设M个子信号分别为M个天线接收，接收信号为：Y1，Y2，.......，YM；对应的时延为Ei，其中i=1，2，3.......，M。依据模型（8）可得下列的方程组：

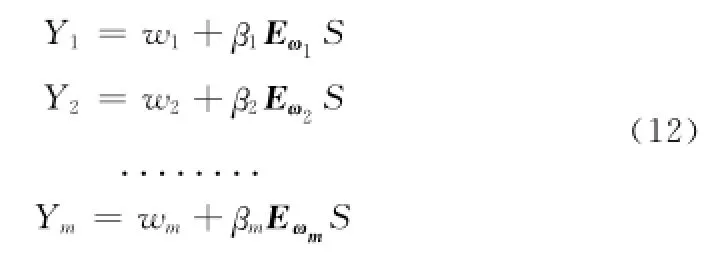
其中：S=Λ［S（ω1），S（ω2），......，S（ωλ）］T为矩阵秩值为λ的对角矩阵，对角线上元素为S（ω）的λ等间隔抽样后得到采样值，Eωi（i=1，2，.....，M）为单位时延矩阵，且满足：

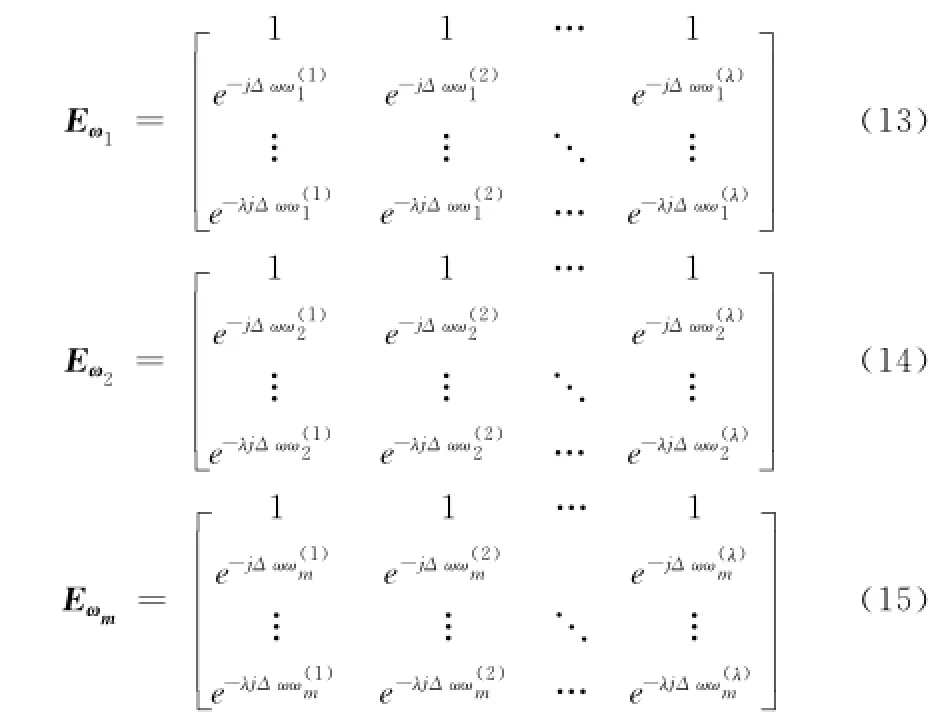
设Δti，j=ti-tj为任意第i根天线与第j根天线到达的时间差，图1中的信号到达方向与法线的夹角θ为信号波达方向DOA。故Δti，j为：

Δti，j=di，jsinθ/c（16）

其中，di，j为第i根天线与第j根天线之间的距离；C为电磁波在真空中的传播速度。

依据上述模型，则DOA的估计¯θi，j满足：¯

θi，j=arcsin（cΔti，j/d）（17）

显然，从模型（16）～（17）可知，TOA估计的越精密，则DOA的估计也就越精密。

因此，对于任意第i路子信号和第j路子信号而言，本文构造关联矩阵Di，j∈Ω2M×M，其模型为：

则式（18）可演变为：

Di，j=w（i，j）+P（ti，tj）B（19）

又设¯C=Di，jDi，jH，Di，jH为Di，j的共轭转置，显然的特征值有2M个。将C按照特征值进行分解：

其中：Ms∈Ω2M×λ为信号空间；Ns ∈Ω2M×（2M-λ）为高斯白噪声空间。

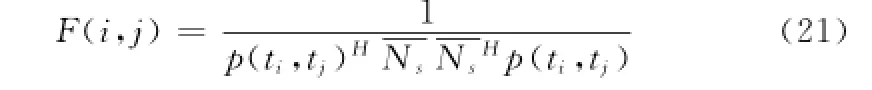
其中：p（ti，tj）为P（ti，tj）的列向量，p（ti，tj）H和分别为p（ti，tj）和的共轭转置。

通过在信号空间内对F（i，j）进行峰值搜索即可获取对任意第i路及第j路子信号的TOA最大估计。

2.2基于接收谱函数的TOA估计

模型（21）中的F（i，j）为任意两路信号同时接收时的接收谱函数。事实上基于亚纳秒级的低强度无线网络信号的各路信号间彼此正交且相互独立，因此可对任意一路信号分别进行接收谱估计。

对于任意一路子信号i而言，其接收信号都可以写为式（12）所对应的Yi形式。令=YiYiH，其中YiH为Yi的共轭转置，显然的特征值有2 M个，将按照特征值进行矩阵分解为信号子空间和高斯白噪声子空间的加权：

其中：eωi为Eωi的列向量。

再依据模型（15）有：

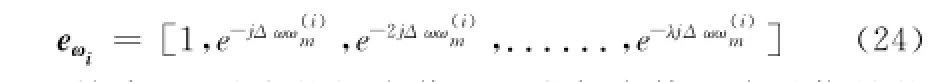
通过搜索fi对应的极大值，即为任意第i路子信号的TOA最大估计。令z=e-jΔωω（i）M，则式（23）的复数表达形式如下所示：

根据复数理论［78］，可知，模型（25）的极点多项式为：

由于模型（27）在复数域上共有2M个复数根，且关于单位圆呈对称分布；且信号子空间的维度为2M-λ。因此的复数根按照接近单位圆的距离，取前2M-λ个复数根1，2，..）作为TOA的估计：

由于DOA估计需要两路信号进行比对，因此据模型（18），可得到任意两路信号i和j对应的关联矩阵D i，j；然后令=D i，j D i，jH，可形成模型（20）。其中∈Ω2M×λ为信号空间，∈Ω2M×（2M-λ）为高斯白噪声空间。

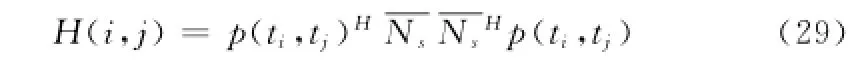
比对函数h（i，j）的表达式如下：

h（i，j）=max H（i，j）（30）

其中：i，j=1，2，3....，M

通过计算最大的代价函数h（i，j），即可得到最佳的径达时间，然后根据模型（17），获取最佳DOA估计。

2.3TOA与DOA参数估计方法

当地面接收设备接收到信号时，首先需要计算各路独立的子信号的解析表达式，然后依据解析表达式得到子信号空间的协方差矩阵，并对矩阵进行信号子空间和噪声子空间分解，以获取特征值和特征向量，并以此进行特征向量估计和特征值估计。当每路子信号都按照该过程计算完毕后，启动比对流程，代入模型（29）后进行比对，获取TOA估计。随后再两两进行比对，获取DOA估计。取TOA估计和DOA估计的最大值，即为整个信号的TOA估计和DOA估计。整个估计方法的构造步骤如下所示。

Step 1：接收子信号，检测子信号是否可以进行抽样处理，获得任意第i路子信号解析表达式Yi（见式（12））；

Step 3：再对模型（25）的复数方程进行零点求解；

Step 4：依据模型（28），得到第i路子信号的TOA估计后，对于剩下的M-1路子信号按照Step 1到Step 3中的步骤依次求取，得到相应的TOA估计，按模型（30）取最大值作为系统的最佳TOA估计；

Step 5：将最佳 TOA估计代入模型（16），求得最佳DOA估计；

Step 6：当本次周期结束，等待下一发送周期开始。

2.4估计精度分析

Ms=［ε1，ε1，...，ελ］（31）

而剩下的特征向量构成噪声空间Ns：

Ns=［ελ+1，ελ+1，...，ε2M］（32）

则信号空间特征向量的误差精度E［ηi，ηi］为：

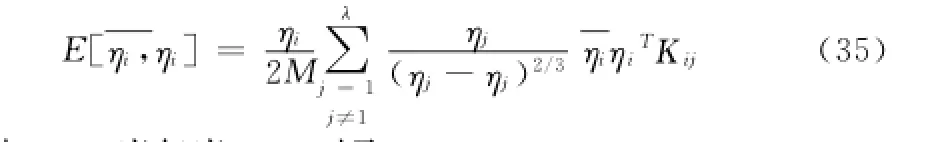
j≠

其中：Κij当仅当i=j时取1。

故将模型 （27）进行Cauchy［9］展开可得：

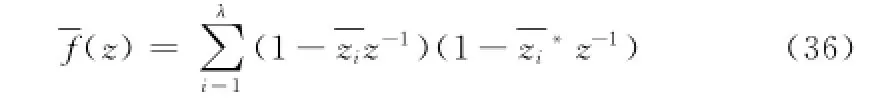
其中：zi的定义与模型（27）相同；zi为f（z）的零点。

其中：Δz为零点的精度估计

对模型（37）进一步化，得到如下模型

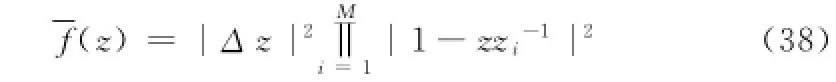
再对模型（38）两端取期望值，可得Δz的估计精度E［| Δz|2］为：

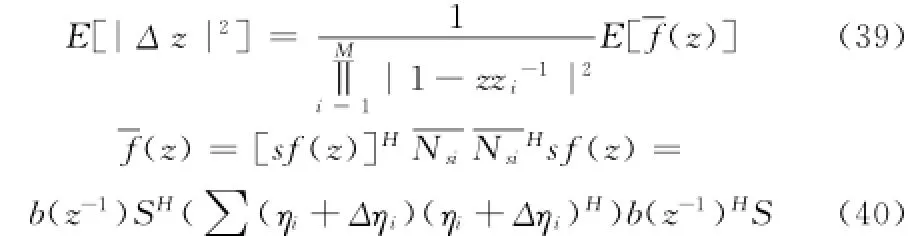
结合模型（35）、模型（39）、模型（40），并设高斯白噪声功率为σ2可得：

由模型（38）可知，TOA估计精度E［|Δt|2］满足：则TOA估计精度为：

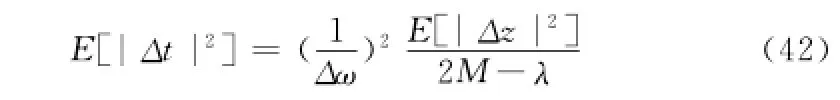
所有参数的物理意义与模型（41）相同

考虑到DOA与TOA的关系满足模型（17），则DOA的估计精度E［|Δθ|2］为：

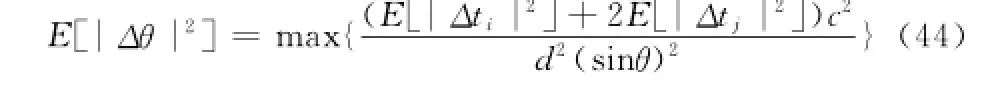
3　仿真实验

本文通过NS2仿真平台对提出的估计方法进行仿真，利用公式（3）生成接收时域信号。仿真参数如表1所示。

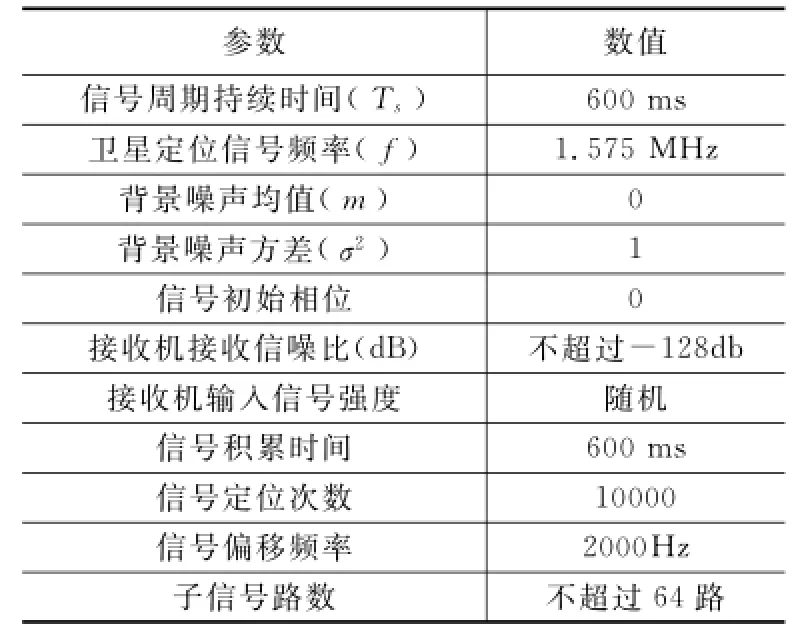
表1　仿真参数表

为验证本文估计方法的优异性，设置对照组为PM算法［10］、ESPRIT 算法［11］。将 本文方法与对 照组 在TOA和DOA估计精度上进行比对。为在尺度上进行比较，按照表1所示的仿真参数表进行仿真环境生成。

图1显示了在不同子信号路数下，本文方法的TOA精度测试。从图中可以看到，随着子信号路数的不断增加，本文方法的TOA精度也在逐渐增加。这是因为本文方法引入了空间解构方式，将接收到的子信号分解为信号子空间和噪声子空间，然后进行特征值评估和零点计算，随着子信号路数的增加，评估的次数也不断增多，因此TOA的精度也得到了相应的提高。

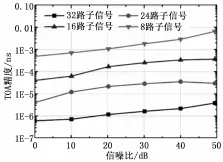
图1　在不同子信号路数下的本文　TOA参数估计精度测试

图2显示了在不同子信号路数下，本文方法在DOA精度上的测试。从图中可以看到，随着子信号路数的不断增加，本文方法的DOA精度也不断增加，这是因为DOA精度与不同子信号之间的TOA精度差值相关，随着路数的增多，单次进行不同子信号之间TOA精度差值对比的精度也随之提高，最后通过不断的对信号的DOA精度进行比对，从而使得DOA精度也得到了提高。

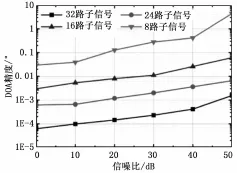
图2　在不同子信号路数下的本文DOA参数估计精度测试

图3显示了在不同接收机信噪比强度下，本文方法和PM算法、ESPRIT算法在TOA估计精度上的测试结果。从图中可以看到随着接收机信噪比的不断提高，3种方法的精度都在下降；但是与PM算法、ESPRIT算法之间的精度差距也在不断的扩大。原因是PM、ESPRIT算法在考虑多径对比时没有引入比对机制；而本文方法在进行接收信号解析时，将信号解析为信号子空间和噪声子空间，且保证在比对之前两者处于正交状态，故减少了背景噪声的干扰，提高了估计的精确度。

图4显示了在不同接收机信噪比强度下本文方法和PM算法、ESPRIT算法在DOA估计精度上的对比。从图中可以看到随着接收机信噪比的不断提高，三者之间的DOA精度上的差距也不断扩大，这是因为本文方法采用的对比和零点计算机制，使得接收信号的DOA精确度同TOA精确度并非直接的线性关系，随着TOA精确度的不断提高，DOA精确度呈现更快的提高服。

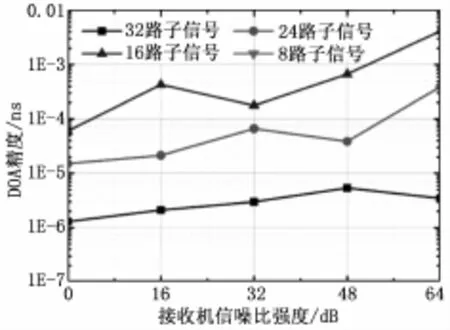
图3　不同接收机信噪比强度下的3种TOA精度估计方法的测试结果

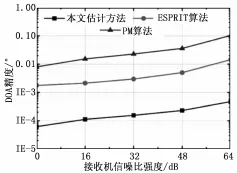
图4　不同接收机信噪比强度下的3种DOA精度估计方法的测试结果

图5、图6显示了在不同背景噪声强度下本文方法和PM算法、ESPRIT算法在TOA上和DOA的估计精度上的对比，从图中可以看到，随着背景噪声强度的不断增加，虽然本文方法的精确度也在下降，但是幅度很小，呈现平稳状态；而PM算法、ESPRIT算法的精确度呈现不断下降的趋势。这是因为随着背景噪声强度的不断增加，背景噪声的功率在接收信号中的比重也不断增加，导致PM算法、ESPRIT算法由于受到噪声影响而降低了精确度。而本文方法引入的正交机制，使得无论背景噪声的强度如何，噪声与信号始终处于正交状态，提高了本文方法的精确度。

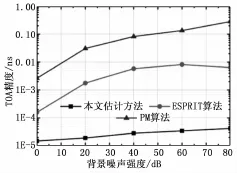
图5　不同背景信噪比强度下的各TOA精度估计方法的测试结果

4　结束语

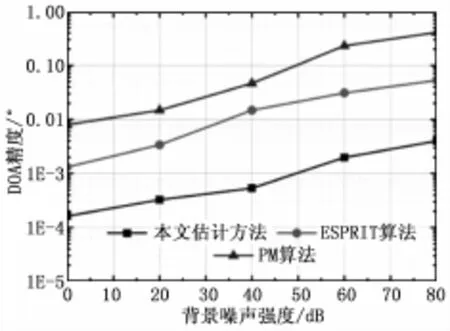
图6　不同背景信噪比强度下的3种DOA精度估计方法的测试结果

本文针对当前网络信号在亚纳秒级TOA与DOA估计精度不高，难以有效抗噪等不足，提出了新的无线网络信号接收谱获取参数估计方法。通过抽样方式，将发射信号抽样为多维独立子信号；随后根据信号的数字特征（特征值和特征向量）进行再次分割，形成相互正交的信号空间及噪声空间，在复数域上实现了有效的零点求取，从而极大的提高了估计精度。仿真结果显示：与PM算法、ESPRIT定位算法相比，本文方法的TOA估计及DOA估计精度更高，具有良好的抗噪声干扰能力。

［1］Wang L，Geng X.A Community-driven Hierarchical Message Transmission Scheme in Opportunistic Networks［J］.Smart Computing Review，2011，1（1）：85-94.

［2］Wang D，Zhang Q，Liu J C.Partial network coding：theory and application for continuous sensor data collection［A］.In Proc.of the 14th IEEE International Workshop on Quality of Service［C］. 2012，35（10）：93-101.

［3］Mani V，Bose R.Direction of arrival estimation of multiple UWB signals［J］.Wireless Personal Communications，2011，57（2）：277-289.

［4］Rovnakova J，Kocur D.Short range tracking of moving persons by UWB sensor network［A］.2011European Radar Conference（Eu-RAD）［C］.2011，23（08）：321-324.

［5］Marzetta T L.Non-cooperative cellular wireless with unlimited numbers of BS antennas［J］.IEEE Trans Wireless Commune，2010，9（11）：3590-3600.

［6］Ngo HQ，Larsson E G，Marzetta T L.Energy and spectral efficiency of very large multiuser MIMO systems［J］.IEEE Trans-Commune，2012，61（4）：1436-44.

［7］Rusek F，Persson D，Lau B K.Scaling up MIMO：opportunities and challenges with very large arrays［J］.IEEE Signal Process Mag，2012，30（1）：40-46.

［8］Jiang H，Cao F C，Ding R.Propagator method-based TOA estimation for UWB indoor environment in the presence of correlated fading amplitudes［A］.4th IEEE International Conference on Circuits and Systems for Communications［C］.2008，17（07）：535-538.

［9］Qin H.H.and Wen D.W.Tikhonov type regularization method for the Cauchy problem of the modified Helmholtz equation［J］. Application of Math&Computer，2009，45（29）：617-628.

［10］Dvorkind T G，Gannot S.Approaches for time difference of arrival estimation in a noisy and reverberant environment［A］.Proceedings of the International Workshop on Acoustic Echo and Noise Control［C］.2003，11（02）：215-218.

［11］Sohn J，Kim N S，Sung W.A statistical model-based voice activity detection［J］.Signal Processing Letters，IEEE，2011，6（1）：1-3.

Study on Estimation of Parameters for Low Intensity Wireless Network Signal Receiving Spectrum

Li Jin1，2，Dai Chunyan1，Hong Yang1
（1.Department of Automation，Baotou Iron and Steel Vocational Technical College，Baotou014010，China；2.College of Information Engineering，Inner Mongolia University of Science and Technology，Baotou014010，China）

In order to solve the problem as low positioning accuracy induced by easily influenced by environmental noise and difficult to obtain precise time estimation and angle estimation in the processing of the low intensity radio network signal of the sub nanosecond level represented by the Beidou satellite navigation signal，the Parameter estimation method of low intensity radio network signal receiving spectrum based on sub-nanosecond was proposed in this paper.Firstly，TOA estimation is obtained by constructing the noise space and the sub signal space，as well as the transmitted signal was sampled by the sampling method.Then，the DOA estimation was obtained by using the complex number field mapping and the TOA estimation.Finally，the accuracy of the proposed parameters estimation method was analyzed.Test data shows that：this proposed method had higher accuracy in TOA and DOA estimation；At the same time，he proposed method can effectively maintain the accuracy of parameter estimation in the case of low signal intensity and severe background noise.This technology can effectively reduce the influence of background noise on signal transmission，and has strong practical significance

wireless network；signal receiving spectrum；DOA estimation，TOA estimation；complex mapping

1671-4598（2016）05-0178-05

10.16526/j.cnki.11-4762/tp.2016.05.051

TP393.04

A

2015-10-24；

2015-12-04。

内蒙古自然科学基金（2013MS0921）。

李瑾（1968-），女，河北冀县人，硕士，讲师，主要从事无线网络、计算机应用方向的研究。