电动舵机非线性系统的辨识研究

田　震，李莹莹，韩　松，卜春光，刘　套

（北京航天无人机系统工程研究所，北京　100094）

电动舵机非线性系统的辨识研究

田震，李莹莹，韩松，卜春光，刘套

（北京航天无人机系统工程研究所，北京100094）

针对所设计的三闭环电动舵机系统，为了提高电动舵机的控制精度，建立具有良好动态性能的电动舵机控制系统，提出了采用非线性系统辨识的方法，并且利用辨识的参数对电动舵机系统进行补偿；根据电动舵机的数学模型分别采用了前馈补偿的方法和反馈辨识的方法对系统的摩擦进行仿真建模研究，利用Lugre模型对系统的摩擦进行辨识，使得系统能够进行自适应摩擦补偿，并且将建模数据加入到电动舵机样机中进行试验验证，经过试验验证，系统的位置跟踪误差和速度跟踪误差均有大幅度减小，验证了非线性模型的准确性及补偿的有效性；试验结果证明，文章所提出的电动舵机非线性辨识研究方法可以准确地实现摩擦模型的建立，并且从该模型出发进行补偿可以有效地提高电动舵机的控制精度。

电动舵机；非线性；Lugre模型；辨识；补偿

0　引言

电动舵机由于其良好的工艺性、可靠性高、便于控制的特点，已经被越来越广泛研究，而且目前在无人机系统中得到了广泛的应用。在电动舵机的设计过程中，一般需要利用系统建模的方式验证控制算法的合理性及有效性，这样可以起到事半功倍的效果。但是电动舵机系统具有非线性的特点，存在很多不利于系统性能提高的因素。例如系统的摩擦力矩、电机力矩的变化、驱动饱和、耦合力矩、干扰力矩、负载变化带来的转动惯量变化所以在数学模型的建立过程中需要考虑利用系统辨识的建模方法，使电动舵机的系统建模更加接近于实际的舵机，实现精确建模。

电机舵机的摩擦对系统的影响是一种强非线性、强耦合关系［6］，所以在系统建模的过程中需要把这种情况考虑进去，以提高系统的跟踪精度。本文所建立的电动舵机数学模型是针对正在研制的某型号无人机系统的电动舵机进行完善的建模，在此模型中充分考虑了电机、减速箱及传动机构摩擦的影响。通过对系统中电机、减速箱及传动机构的非线性进行辨识，采用前馈补偿及逆模型补偿方法对系统中的摩擦进行补偿控制。仿真和实验结果表明，本文所提出的辨识和补偿方法能够有效地减小摩擦非线性对舵机系统跟踪精度的影响。

1　数学模型的建立

1.1系统组成及原理

本文所设计电动舵机伺服系统用于无人机的副翼、尾翼及垂尾，它是由控制器、驱动器（功率放大器及三相桥驱动）、电机、行星齿轮减速箱、摇臂、位置传感器等组成。图1是电动舵机结构连接示意图，电机的输出轴连接减速箱，减速箱采用的是行星齿轮减速箱，其输出轴与摇臂进行连接，电位计输出轴与减速箱输出轴通过传动机构进行连接。

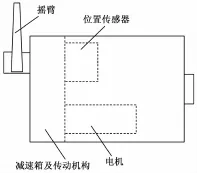
图1　舵机结构连接示意图

此舵机系统是由位置环、电流环和速度环3个闭环回路组成，位置环构成舵机系统的主反馈；速度环构成速度的负反馈，用于改善系统阻尼，提高系统刚度；电流环构成电流负反馈，以改善转矩控制线性度，提高快速性；抑制电源扰动，限制过流，减小功率放大器死区，提高线性度，保证控制性能。整个电动舵机工作原理是电动舵机接收来自于飞控计算机的舵偏角控制指令，然后由舵机控制器进行解算控制电机进行转动，控制相应的飞机舵面进行偏转，使得飞机能够稳定的飞行和执行侦察任务，舵机控制器同时采集电动舵机的位置、速度和电流，对舵机实现精确控制，控制流程如图2所示。

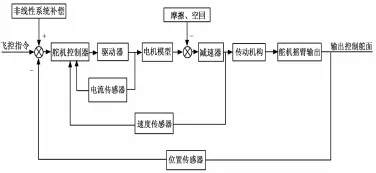
图2　控制流程图

1.2电动舵机的数学模型

利用SIMULINK进行建模主要是从以下几个方面出发：

1）系统的控制算法建模；

2）前馈补偿环节的建模；

3）电机系统的建模；

4）系统减速箱和传动机构的建模。

由以上四点得到的电动舵机的模型如图3所示，常规的线性舵机建模不包括前馈补偿环节和摩擦的扰动，本文的建模中将这些非线性环节加入进去，然后需要辨识系统的摩擦。

图4部分是电机的Simulink模型。

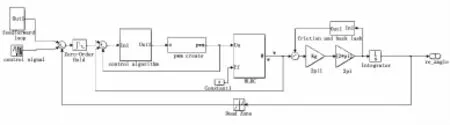
图3　电动舵机simulink模型

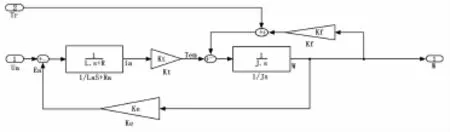
图4　电机部分simulink模型

1.3非线性参数来源

电动舵机作为一个伺服系统，它不可避免的会引入间隙和摩擦。间隙是减速箱齿轮与齿轮之间的间隙和轴承之间的间隙，根据系统指标是0.5°；摩擦主要来自于电机、行星齿轮减速箱内部齿轮间的摩擦及传动机构，它是一种比较难以辨识的非线性系统，会对系统的位置和速度跟踪精度产生影响，本文需要进行针对摩擦这种非线性状态进行辨识。

2　非线性参数辨识

2.1非线性模型建立

本文所采用的建模方法是使用Lugre摩擦模型，它引入鬃毛假设理论来进行摩擦行为的模拟，全面的描述了滞滑运动效应、Striback效应、黏弹效应和预变形效应，它是同时综合了Striback效应和Dahl模型［1］。Stribeck效应是指在极低的速度区段内，摩擦力会随着速度的增加而减少，它是出现滞-滑运动的主要原因；Dahl摩擦模型是将停滞状态下的摩擦特性看成是一种类似弹簧特性的动态摩擦模型［3］。

Lugre摩擦模型表达式

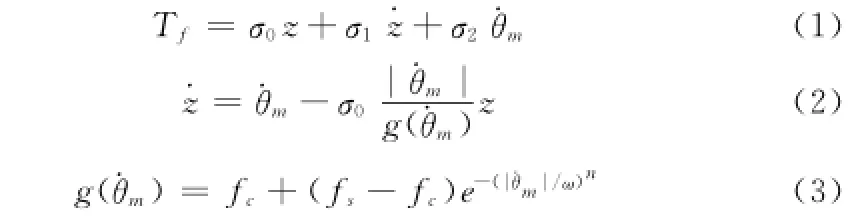
z是鬃毛的平均形变量，σ0是鬃毛的等效刚度，σ1是微观黏滞摩擦阻尼系数，σ2是宏观黏滞摩擦阻尼系数，fc表示库仑摩擦力矩，fs是最大静摩擦力矩，ω是Stribeck角速度，n为Stribeck曲线形状和陡度的影响因子，一般取1或2。

整个舵机系统的数学模型

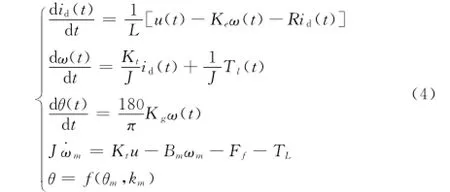
J是电动舵机系统折合到电机轴上的总转动惯量，L、R是电机的电枢电感和电阻，θ和θm分别是舵机摇臂转动角度和电机的转角。

采用上述Lugre模型结合实验可以测得Stribeck曲线形状和陡度的影响因子n可以取1，负载所受到的摩擦力矩（此处的负载是指电动舵机减速箱和传动机构）：

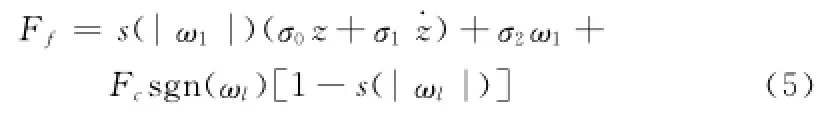
此处需要设置舵机摇臂的角度输出是存在边界，根据系统指标要求是-40°～+40°，负载干扰力矩TL同样存在边界TL＜λn，其中λn为正常数。

2.2非线性参数辨识

通过对整个系统摩擦的分析和对Lugre模型的研究需要从两个方面对摩擦进行辨识：静态参数辨识和动态参数辨识。

1）静态参数包括fc、fs、ω和σ2。

假设电动舵机工作在匀速转动的状态，.z此时为0

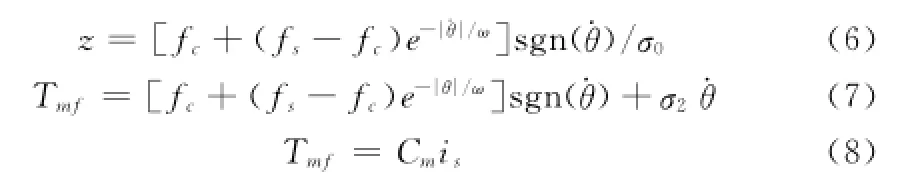
采用最小二乘法来拟合曲线，使拟合曲线与测试数据点之距离的平方和最小，是系统电流乘以转矩系数可得系统的摩擦转矩［12］，即可辨识出Lugre的摩擦系数，如表1所示。

表1　静态参数辨识

2）动态参数辨识：

当舵机处于粘滞摩擦状态时，此时舵机的驱动力矩小于系统的静摩擦力，可得

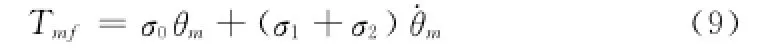
进行拉氏变换可得

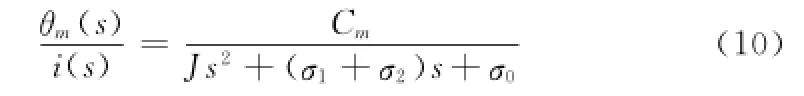
通过上式可得系统在粘滞状态下时，系统所受到的摩擦近似于一个二阶阻尼系统，当输入低幅值阶跃电流信号时可以得到其阶跃响应曲线求得J、σ1+σ2，进而能够实现Lugre摩擦的动态参数的辨识。所得参数如表2所示。

表2　Lugre摩擦的动态参数

通过辨识的方法得到了Lu Gre摩擦模型所有静态参数和动态参数，通过上述分析可知鬃毛变形量z是关于电机转速口.θm的隐式函数，如式（11）所示。

.z=f（.θm，z）（11）

因此，在舵机初速度为0的条件下可利用迭代法能够对Lu Gre模型状态变量z实现辨识。

3　非线性系统仿真与试验验证

通过上述辨识出的非线性参数，结合此电动舵机的系统设计指标，将辨识所得结果带入前文图3所示的simulink模型，同时将舵机减速箱间隙值0.5°带入到simulink仿真中，进行电动舵机的仿真模型的补偿和优化。此仿真分析用来研究摩擦非线性对舵机系统性能的影响以及验证补偿方法的有效性。

本设计中所选用的电机为MAXON的EC系列电机具体参数如表3所示。

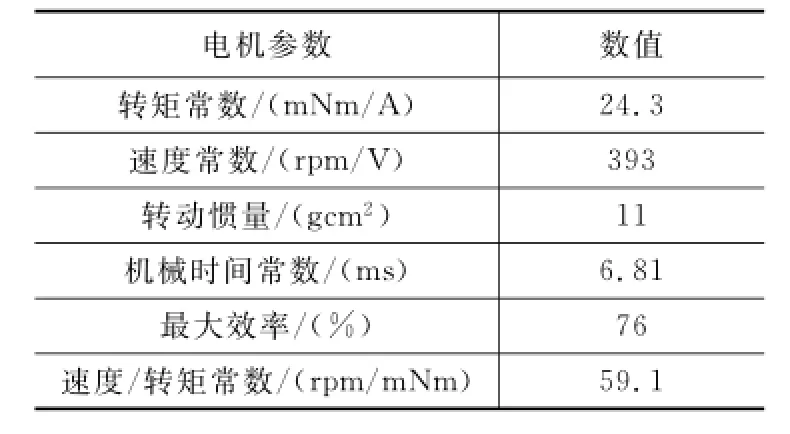
表3　电机参数

电机转子及其负载折算到电机轴上的总转动惯量为13.4 g·cm2，摩擦力矩是LuGre模型，系统是位置、速度和电流的三闭环控制系统，无人机系统要求的指标舵机运行指标是幅值1°、频率5 Hz，仿真结果如图5和图6所示，从仿真结果可以看出，因为Lu Gre摩擦非线性的影响，当没有加入补偿时，系统正弦运动在速度过零时位置跟踪曲线出现了波形失真的现象，并伴有小幅值振荡现象，其跟踪误差出现了尖峰。当对摩擦进行前馈补偿后，上述现象基本消失，跟踪误差得到了有效的减小。

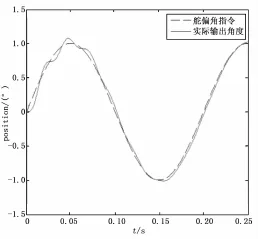
图5　加入补偿之前位置跟踪图

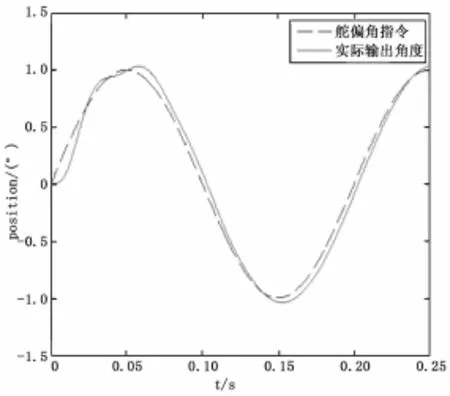
图6　加入补偿之后位置跟踪图

为了充分验证这一仿真结果，将样品电动舵机放入舵机综合测试台，本测试台是由工控计算机系统、PCI多功能数据采集卡、高速串口卡、数字舵机测试接口箱、直流电源、舵机安装台、扭矩测试仪及光电编码器组成。此测试台能够实现对舵机的位置、速度和扭矩的测试。将上述辨识方法所得到的数据加入到电动舵机软件中，利用此测试台对舵机的位置和速度进行了测试，得到的测试结果如表4所示。

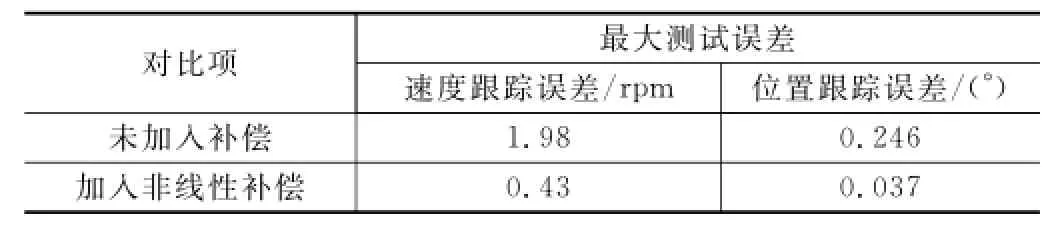
表4　误差对比

结果对比可知加入了非线性辨识进行补偿真正的减小了系统的跟踪误差，准确的描述了实际舵机的运行状态。通过对非线性进行补偿，提高了系统的跟踪精度，验证了非线性模型的准确性及补偿的有效性。

4　结束语

经过实验验证，本文提出的电动舵机系统的非线性辨识方法提高了电动舵机系统的准确性，通过仿真建模证明了利用Lugre摩擦模型辨识的方法进行补偿提高了系统的控制精度。然后在仿真的基础上，将非线性辨识的结果加入到电动舵机样机中，发现加入非线性补偿后，可以消除非线性环节对舵机实际带来的不利影响，验证了非线性模型和补偿的准确性和有效性，为此电动舵机的进一步改进和定型研究奠定了基础。

［1］Canuda C，Olsson H，Astrom K J，et al.A new model for control of systems with friction［J］.IEEE Transaction on Automatic Control，1995，40 （3）：419-425.

［2］Erkorkmaz K，Altintas Y.High speed CNC System Design.Part II：Modeling and Identification of Feed Drives［J］.International Journal of Machine Tools& Manufacture，2001，41 （10）：1487-1509.

［3］于志伟，曾鸣，乔大鹏.采用复合控制的直流力矩电机摩擦补偿［J］.电机与控制学报，2008，12 （5）：539-544.

［4］Minh T N，Ohishi K，Takata M.Adaptive friction compensation design for submicrometer positioning of high precision stage［A］.//International Congress of Mathematicians ［C］.IEEE. Kumamoto，Japan，2007：1-6.

［5］张宇河，董宁.计算机控制系统［M］.北京：北京理工大学出版社，2004.

［6］Yanada H O H.Frequency-shaped sliding mode control of an electrohydraulic servomotor［J］.Journal Of Systems And Control and Dynamics.1999，213 （1）：441-448.

［7］Sridhar Seshagiri H K K.On Introducing Integral Action in Sliding Mode Control［C］.Las Vegas，Nevada USA：2002.

［8］于志远.旋转弹执行机构的研究［D］.北京：北京理工大学，2009.

［9］况荣华，荣太平.一种新型PID参数自适应模糊控制器［J］.华中科技大学学报，2001 （6）：25-26.

［10］夏长亮.无刷直流电机控制系统［M］.北京：科学出版社，2009.

［11］张新刚.基于扩展Stribeck效应的摩擦实验建模及系统动力学研究［D］.上海：上海交通大学，2009.

［12］姚建勇，焦宗夏.改进型LuGre模型的负载模拟器摩擦补偿［J］.北京航空航天大学学报，2010，36（7）：812-815.

Study of Identification for Nonlinear System of Electronic Actuator

Tian Zhen，Li Yingying，Han Song，Bu Chunguang，Liu Tao
（Beijing Institute of Engineering of Aerospace UAV System，Beijing100094，China）

For the design of the three closed-loop motor servo system included position，speed and current，in order to improve the control accuracy of system and good dynamic performance of control system，the method of the nonlinear system identification is raised.According to the mathematical model of the system，the method of feedforward compensation and feedback identification is used.Lugre model for friction and the identification of backlash are applied.The system can perform adaptive friction compensation.following error of the position and speed of the system is greatly reduced.It verifies that the nonlinear model is accurate and the compensation is effective.The result of the experiment shows that the proposed identification methods can accurately realize the identification of friction and backlash.Besides，it can improve the control accuracy of electronic actuator effectively.

electric actuator；system of nonlinearity；Lugre model；identification；compensation

1671-4598（2016）05-0110-03

10.16526/j.cnki.11-4762/tp.2016.05.032

T13

A

2015-12-13；

2015-12-24。

田震（1989-），男，天津人，工程师，主要从事伺服系统方向的研究。

李莹莹（1987-），女，黑龙江宁安人，工程师，主要从事伺服系统方向的研究。