大跨度叠合梁斜拉桥施工控制参数敏感性分析
2016-11-22黄志霜
肖 雄, 黄志霜
(西南交通大学土木工程学院, 四川成都 610031)
大跨度叠合梁斜拉桥施工控制参数敏感性分析
肖 雄, 黄志霜
(西南交通大学土木工程学院, 四川成都 610031)
为深入研究大跨度叠合梁斜拉桥施工控制参数的敏感性,以临海高等级公路灌河大桥为背景,采用有限元软件MIDAS Civil建立全桥三维有限元模型,分析了各设计参数对大跨度叠合梁斜拉桥主梁成桥线形和主梁应力的影响。研究结果表明:桥面板重量、钢主梁梁重以及斜拉索弹性模量对该桥主梁成桥线形和主梁应力有显著影响;桥面板弹性模量和钢主梁弹性模量对该桥成桥状态影响不大。
斜拉桥; 叠合梁; 施工控制; 设计参数; 敏感性分析
大跨度桥梁施工控制的主要目的,就是为了保证桥梁的施工安全以及成桥后主梁的线形和受力状态均满足设计要求[1]。斜拉桥属高次超静定结构,其施工控制是一项复杂的系统工程,多种因素均可能对施工控制结果产生重要影响,通过数值模拟分析得到的桥梁结构各施工阶段的理想状态与结构的实际状态之间总是存在着一定的误差[2-4]。结构参数敏感性分析的主要目的就是确定关键控制参数,为大跨度桥梁施工过程中的仿真分析、参数识别、模型修正以及误差分析等研究工作提供基础[3]。
叠合梁斜拉桥主梁采用钢-混凝土组合截面,具有优越的受力性能和施工性能,对此类桥型进行施工控制参数敏感性分析具有重要意义。本文以临海高等级公路灌河大桥为例,通过数值模拟着重对结构重量、材料弹性模量等重要参数进行成桥阶段桥梁结构响应的敏感性分析,以确定结构的主要控制参数,为大跨度叠合梁斜拉桥施工控制方案的制定及最优控制决策提供科学依据。
1 工程概况
灌河大桥是临海高等级公路跨越灌河的重要工程,主桥(60.8+117.2+400+117.2+60.8)m采用双塔双索面半漂浮体系钢-混凝土叠合梁斜拉桥(图1)。主梁采用双边“工”字型主梁结合桥面板的整体断面,全宽36.5 m(图2);索塔采用H型索塔,塔高167.5 m;索塔两侧各17对斜拉索,按双索面扇形布置。

图1 灌河大桥主桥示意(单位:m)

图2 主梁标准横断面(单位:mm)
2 有限元模型
采用有限元软件MIDAS Civil建立全桥三维有限元模型,斜拉索以只承受轴向力的桁架单元模拟,主梁采用施工阶段联合截面(同一单元不同施工阶段对应不同截面)模拟,索塔采用空间梁单元模拟,斜拉索在下锚点通过刚臂单元分别与主梁连接,上锚点通过刚臂单元与索塔直接相连(图3)。
图3 灌河大桥有限元模型
3 参数敏感性分析
分析在某一个单一参数发生变化而其余参数不变的情况下,全桥的线形、内力等关键参数随之发生的变化情况,从而选出对结构的线形和内力状态影响较大的参数,进而在施工过程中加以严格的监测和控制[5~6]。
选取桥面板重量、钢主梁梁重、桥面板弹性模量、钢主梁弹性模量以及斜拉索弹性模量等5个结构参数,分析其对主梁成桥线形和主梁应力的影响程度。
3.1 桥面板重量
考虑桥面板模板变形或混凝土欠、超浇注均会引起重量变化,然而有限元模型一般不进行截面的修正,故将其重量变化转换为混凝土容重的变化[7]。分别考虑桥面板容重增大5 %和减小5 %时,分析其对成桥状态结构响应的影响情况。
3.1.1 主梁成桥线形
桥面板容重的变化对主梁成桥线形的影响如图4所示。由图可知,桥面板容重增大5 %和减小5 %时,主梁成桥线形变化明显,线形变化最大值将近80 mm,出现在跨中合拢段附近。

图4 桥面板容重增减5%时主梁线形的变化
3.1.2 钢主梁应力
桥面板容重的变化对钢主梁应力的影响如图5所示。桥面板容重增加5 %时,主梁的最大压应力为144.935 MPa,最大拉应力为-81.344 MPa,最大应力增量为23.189 MPa;桥面板容重减小5 %时,主梁的最大压应力为136.766 MPa,最大拉应力为-109.398 MPa,最大应力增量为23.203 MPa。

图5 桥面板容重增减5%时主梁下缘应力变化
由图5分析可知,钢主梁下缘应力最大变化量接近25 MPa,在塔周无索区和跨中附近变化相对较小,在1/4跨附近影响最为显著。
3.2 钢主梁重量
虽然钢主梁自重荷载相对容易控制,误差不会太大,但是对于大跨度叠合梁斜拉桥而言,由于跨度较大、整体刚度较小,结构的响应对梁重变化非常敏感。因此,分别考虑钢主梁容重增大和减小5 %时,分析其对成桥状态结构响应的影响情况。
3.2.1 主梁成桥线形
钢主梁容重的变化对主梁成桥线形的影响如图6所示。钢主梁容重增大5 %和减小5 %时,主梁成桥线形变化明显,最大变化值33 mm发生在跨中附近。

图6 钢主梁容重增减5%时主梁线形的变化
3.2.2 钢主梁应力
钢主梁容重的变化对钢主梁应力的影响如图7所示。由计算分析得出,钢主梁容重增加5 %时,主梁的最大压应力为139.973 MPa,最大拉应力为-80.359 MPa,最大应力增量为10.28 MPa;钢主梁容重减小5 %时,主梁的最大压应力为141.735 MPa,最大拉应力为-97.517 MPa,最大应力增量为10.198 MPa。
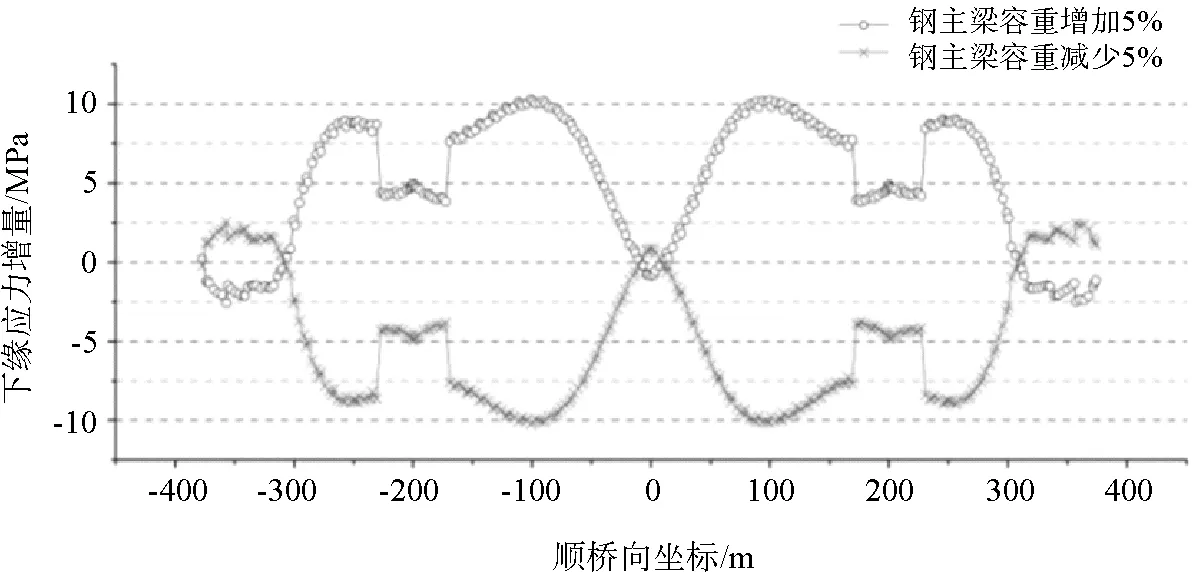
图7 钢主梁容重增减5%时主梁下缘应力变化
由图7分析可知,钢主梁下缘应力变化较大,在塔周无索区和跨中附近其变化值接近0,在1/4跨附近变化最为明显。
3.3 桥面板弹性模量
桥面板作为叠合梁斜拉桥主梁的一部分,在最后的成桥阶段要参与主梁整体受力,其弹性模量的大小影响内力在钢-混凝土叠合梁主梁内的内力分配,因此必须作为一项重要参数加以识别[4]。基准状态桥面板弹模为3.55×104MPa,分别考虑其增大5 %和减小5 %时,分析其对成桥状态结构响应的影响情况。
3.3.1 主梁成桥线形
桥面板弹模变化对主梁成桥线形的影响如图8所示。由图可知,当桥面板弹模增加5 %和减少 5 %时,主梁成桥线形变化较小,最大变化值仅2 mm发生在跨中附近。

图8 桥面板弹性模量增减5%时主梁线形变化
3.3.2 钢主梁应力
桥面板弹模变化对钢主梁应力的影响如图9所示。当桥面板弹模增加5 %时,钢主梁最大压应力为139.0 MPa,最大拉应力为-89.8 MPa,最大应力增量为2.5 MPa,变化幅度为5.4 %;当桥面板弹模减小5 %时,主梁最大压应力为142.8 MPa,最大拉应力为-86.9 MPa,最大应力增量为2.7 MPa,变化幅度为5.2 %。即桥面板弹性模量的变化对钢主梁应力的影响很小。

图9 桥面板弹性模量增减5%主梁下缘应力变化
3.4 钢主梁弹性模量
钢主梁弹性模量直接影响内力在叠合梁主梁内的内力分配,因此,有必要对其进行敏感性分析。基准状态钢主梁弹模为2.06×105MPa,按钢主梁弹模增大5 %、减小5 %两种情况,分析其对成桥状态的影响程度。
3.4.1 主梁成桥线形
钢主梁弹模变化对主梁成桥线形的影响如图10所示。由图可知,当桥面板弹模增加5 %和减少5 %时,主梁成桥线形变化较小,最大变化值仅2 mm出现在靠近桥塔边跨侧的梁段。总体看来,钢主梁弹性模量对主梁成桥线形的影响很小。

图10 主梁弹性模量增减5%时主梁线形的变化
3.4.2 钢主梁应力
钢主梁弹模变化对钢主梁应力的影响如图11所示。当钢主梁弹模增加5 %时,钢主梁最大压应力为143.8 MPa,最大拉应力为-89.1 MPa,应力最大变化量为3.7 MPa,变化幅度为4.6 %;当钢主梁弹模减小5 %时,主梁最大压应力为137.8 MPa,最大拉应力为-87.7 MPa,应力最大变化量为3.8 MPa,变化幅度为5.1 %。总体而言,钢主梁弹性模量的变化对主梁应力的影响很小。

图11 主梁弹性模量增减5%时主梁上缘应力变化
3.5 斜拉索弹性模量
按斜拉索弹模增加5 %、减小5 %两种情况考虑,基准状态拉索弹模为1.95×105MPa,两种变化均以基准状态得到的安装线形为计算的初始线形。
3.5.1 主梁成桥线形
拉索弹模变化对主梁成桥线形的影响如图12所示。由图可知,当钢主梁容重增加5 %和减小5 %时,主梁成桥线形变化出现明显峰值,最大变化值20 mm发生在跨中梁段。

图12 拉索弹性模量增减5%时主梁线形的变化
3.5.2 钢主梁应力
斜拉索弹模变化对钢主梁应力的影响如图13所示。当拉索弹模增加5 %时,主梁最大压应力为140.5 MPa,最大拉应力为-85.7 MPa,应力最大变化量为2.9 MPa,变化幅度为5.3 %;当拉索弹模减小5 %时,主梁最大压应力为141.2 MPa,最大拉应力为-91.3 MPa,应力最大变化量为3.1 MPa,变化幅度为5.0 %。
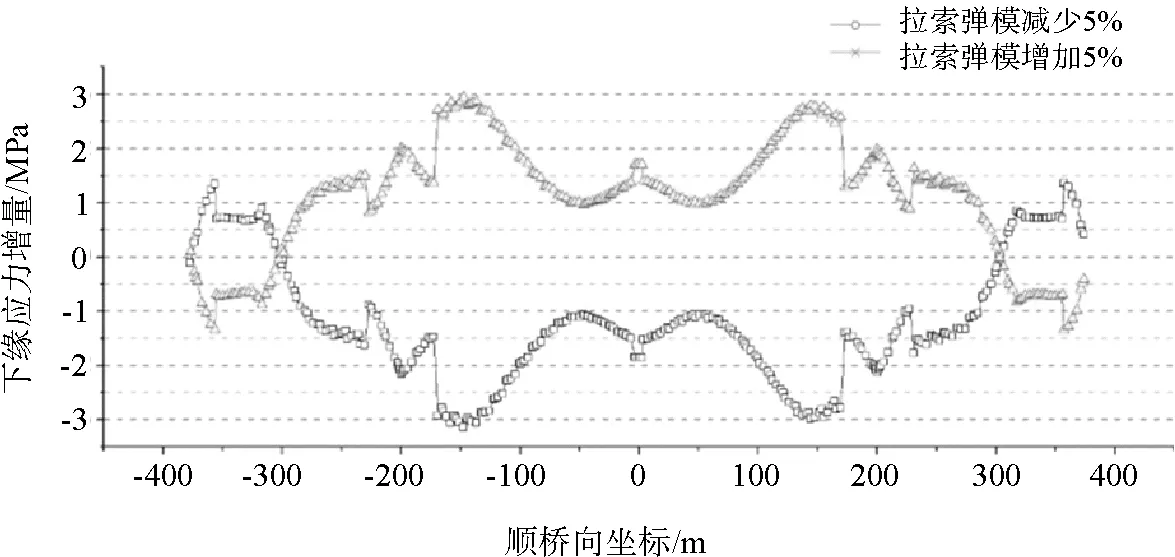
图13 拉索弹性模量增减5%时主梁下缘应力变化
由图13可以看出,斜拉索弹性模量的变化对钢主梁应力的影响均在3 MPa之内,影响较小。
4 结 论
(1)桥面板重量、钢主梁梁重、斜拉索弹性模量等结构参数是影响主梁成桥线形和主梁应力的主要控制参数,而桥面板及钢主梁的弹性模量对结构成桥线形和主梁应力影响较小。
(2)相对主梁应力而言,大跨度叠合梁斜拉桥主梁线形对结构参数的变化更为敏感,因此在施工控制过程中,应着重对结构线形加以严格监控。
(3)在实际工程中,尤其是大跨度叠合梁斜拉桥这类特殊结构,应针对主要控制参数进行实时监控调整,以减小其对桥梁结构的不利影响。
[1] 徐君兰. 大跨度桥梁施工控制[M].北京:人民交通出版社,2000.
[2] 赵雷,孙才志,陈文元. 大跨度结合梁斜拉桥的参数敏感性分析[J]. 世界桥梁,2011(6):38-41.
[3] 李乔,卜一之,张清华. 大跨度斜拉桥施工全过程几何控制概论与应用[M]. 成都:西南交通大学出版社,2009.
[4] 黄坤全,刘人铭. 叠合梁斜拉桥成桥过程的参数敏感性分析[J]. 交通科技,2011(4):1-4.
[5] 张乘,张鹏,刘涛涛. 多塔斜拉桥成桥状态参数敏感性分析[J]. 四川建筑科学研究,2014,40(2):55-57.
[6] 黄灿,赵雷,张清华. 特大跨度斜拉桥制造阶段参数敏感性分析及工程应用[J]. 四川建筑科学研究,2011,37(3):297-300.
[7] 武芳文,赵雷. 大跨度斜拉桥施工力学行为参数敏感性分析[J]. 兰州理工大学学报,2009,35(6):124-130.
肖雄(1992~),男,硕士研究生,从事大跨度桥梁结构施工控制理论与实践研究。
U448.21+5
A
[定稿日期]2016-05-06
