利用优化算法对合成孔径激光雷达相位误差补偿的研究

张鸿翼，李 飞，徐卫明，舒 嵘

(中国科学院上海技术物理研究所空间主动光电技术重点实验室,上海 200083)



利用优化算法对合成孔径激光雷达相位误差补偿的研究

张鸿翼，李 飞，徐卫明，舒 嵘

(中国科学院上海技术物理研究所空间主动光电技术重点实验室,上海 200083)

在遥感领域，平台振动是合成孔径激光雷达(SAL)研究中的一个重要问题.目前尚没有针对SAL的平台振动补偿方法.根据对振动机理分析，平台振动的影响体现在相位误差上. 根据对振动机理的分析，可以利用多项式描述平台振动带来的相位误差. 基于这一转化模型利用优化算法对多项式系数进行优化求解可以达到补偿效果。优化过程需要选取合适的目标函数，用优化后的求解结果补偿回波数据相位，补偿结果再用匹配滤波器进行压缩.通过仿真和实验证明，用优化算法实现相位误差补偿可以达到很好的压缩效果.研究工作为平台振动补偿技术提供了一项选择.

遥感；相位误差；振动补偿；优化算法；多项式

1 引言

合成孔径激光雷达(SAL)是近年来较为热点的一个研究方向，是实现厘米量级超高分辨率的唯一光学手段，具有成像速度高、图像可视性好、天线尺寸小等优点[1].相较于微波载波的合成孔径雷达(SAR)，SAL的激光载波相较于微波短3～4个数量级[2]，可以突破微波雷达的衍射极限，为更高分辨率的成像提供了可能.采用激光载波带来的问题是更短的波长对平台振动问题更为敏感,并且难以补偿[3].传统的用于基于微波波长的平台振动补偿方法不再适用于SAL，因此平台振动的补偿技术是SAL研究的关键技术之一.

平台振动会对SAL成像的相位信息带来干扰，表现为接收方位向脉冲之间的相对相位变化紊乱.文献[2]定性地分析了平台振动对成像质量的干扰，得到结论是振动的幅度，频率和初始相位分别对成像质量有较大影响，可以用峰值加速度来描述振动大小；文献[4]分析了平台振动对成像压缩影响的具体体现，得出结论是垂直于航向的振动对成像影响较大，影响主要体现在方位向压缩展宽；文献[5]提出针对展宽现象使用PGA算法对成像结果进行聚焦处理的算法.参考美国洛克马丁公司的飞行实验[6]，在平台振动条件下的成像采用的是减振平台配合PGA算法实现的.

对SAL成像回波的相位误差抑制的思路之一是使用差分系统，文献[7]中提出的一种通过光外差进行振动自抑制方法是值得研究的，该成像系统对来自平台振动和大气扰动以及激光源线宽带来的相位误差都有抑制作用，其效果有待在实际工程中验证.另外还有美国于09年提出的差分合成孔径激光雷达(DSAL)的概念[8]，采用两个接收镜头在方位向前后排列的结构，通过对两个接收镜头光程差的累加实现相位的抑制.但是由于接收镜头尺寸一般比较大，符合差分条件的两个镜头之间在结构实现上有很大难度，该抑制方法的工程实现有待进一步论证.以PGA算法为代表的自聚焦算法也是广泛使用于雷达成像补偿的算法[9]，对相位误差带来的散焦有一定的补偿效果，但是该算法适用于成像结果的聚焦和优化，不适合替代数据压缩算法.

本文提出一个基于成像结果评估的优化算法补偿的思路.利用多项式拟合相位误差，使用优化算法通过压缩质量调整多项式参数补偿数据相位，直到达到最佳压缩效果.并针对这一算法进行了仿真验证和实验验证.

2 振动误差分析与多项式建模

为简化分析模型，我们取一个固定距离门的慢时间数据当作研究对象，深入分析回波数据变化的特点.

在理想状态下，对于单一目标而言，飞机在一个合成孔径长度内光程是按照如下规律变化的：

(1)

其中tm是慢时间，Rs是光束平面上垂直于航迹的长度，Xn是点目标在飞机飞行的方位向上的投影位置，正侧视的时候Xn为0，V为飞行速度.根据公式

(2)

我们可以计算光程的变化，其中fc为载波频率.可以将相位变化近似为：

(3)

其中，α是理想状态下的高次量，在压缩过程中是可以忽略的.考虑到相位误差问题，我们需要在上述模型中加入相位误差：

=φexp(tm)+φv(tm)

(4)

其中为φv(tm)是随着tm变化的来自平台振动等因素带来的相位误差，根据高精度惯性导航仪(POS)记录的“运12”型号飞机的一次飞行中的平台振动数据中的一段解算其相位变化可以看出，φv(tm)变化范围相较于φexp(tm)要大一个数量级以上.

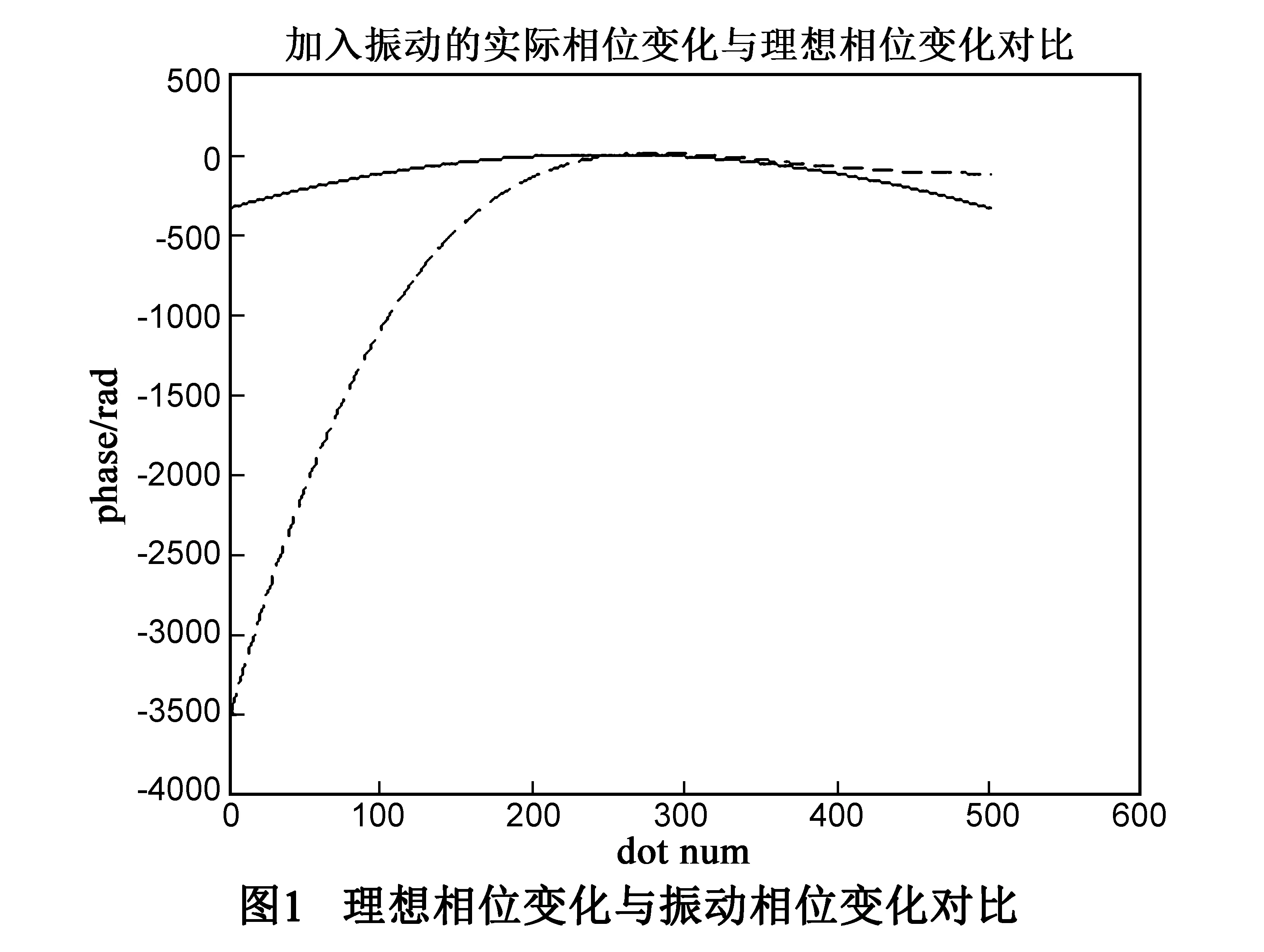
图1中实线为理想的相位变化，虚线为加入振动之后的相位误差变化，可以看到，振动带来的相位变化幅度是远大于理想状态下相位变化幅度的.

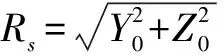
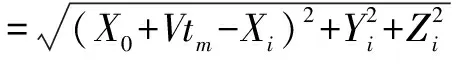
(5)

Sexp(tm)

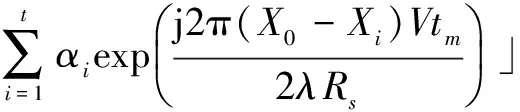
(6)

式(5)中αi表示第i个目标经过散射到接收镜里的能量，不同的目标具有不同的αi.式(6)中的近似用到了泰勒展开，忽略了高次项，在正侧式时认为X0=0.式(6)表示目标分布位置不同对接收数据相位贡献的不同分量，如果不考虑Xi，在光学足印中所有目标的能量都是正叠加，不同Xi的取值在接收端接收的能量由于相互之间的角度不同则会呈现出波动.经过分析我们可以看出，平台振动带来的光程变化对接收数据的影响主要体现在对接收数据相位变化的污染上.根据公式很容易推算，光程差的变化对接收的能量影响很小.

根据式(6)绝对值号中的推导可以看出，理想状态下的数据是特定的相位分布与特定的能量起伏组合得到，由于振动带来的误差污染了相位分布，但是并没有污染能量信息的变化，理论上是可以根据能量的分布将相位的分布恢复出来的.

由式(4)中φv(tm)与φexp(tm)相比很大，在经过相位解缠绕之后无法恢复出来φv(tm)变化趋势.由于飞机机械惯性很大，根据实测的POS数据显示飞机沿着理想航线的偏移都是在很低的频率下发生的，量级在0.1Hz；而飞机的机械振动相对频率较高，根据文献[10]的分析，现有的机械振动平台精度在50μm左右，而振动频率在20Hz～2kHz，振动频谱能量分布在低频，频率越高，频谱能量越小.以机载飞行速度为50m/s，孔径长度为1m计算，PRF(pulse recurrence frequency)典型值为30kHz左右，可以看出，机械振动和航线偏移频率都小于PRF一个数量级以上.

3 优化算法用于基于多项式模型的相位误差补偿

相位误差变化是来自于平台的机械振动，根据POS的实测数据分析，机械振动具有变化频率较低，运动曲线平滑连续的特点，对应的相位误差也呈现出平滑连续的特点，按照SAR的处理算法，可以采用多项式描述运动过程中相位变化曲线[11，12],可以使用多项式描述平台振动导致的相位误差：

(7)

φ(tm)=φexp(tm)+φv(tm,n)

(8)

由于振动相较于PRF处于低频，相位误差的变化率比较低，在式(8)中可以用有限的项数来描述其变化，如果参数构造得当，在得到的数据相位中减去多项式构造的相位变化曲线即可恢复出理想状态的相位变化.再对经过相位补偿的数据进行压缩.

用多项式描述的相位误差将误差补偿问题转化为寻找合适的补偿参数向量p(n)的优化问题.由于振动具有随机性，而且p(n)的不一定要求出最优解，所以可以采用启发式算法寻找最优p(n).这里使用遗传算法：

遗传算法是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法.适用于解决复杂的非线性和多维空间寻优问题[13],基本运算步骤包括初始化，个体评价，选择运算，交叉运算，终止条件判断等步骤等.

本工程调用遗传算法时需要考虑如下问题：

(1)多项式系数的编码描述：遗传算法通过遗传编码对待优化参数进行描述.多项式系数之间是高度缠绕的.在拟合过程中，变化其中一项意味着其他项数都要跟着变化.不能直接采用多项式系数当作编码进行优化.

这里采用Legendre多项式对相位误差进行描述.Legendre多项式描述如下[14]：

(9)

式(9)具有多项式的形式，称Pk(x)为k阶Legendre多项式，可以看出，由Legendre多项式的组合可以描写各个阶的多项式的数值.Legendre多项式在-1到1之间存在正交性：

(10)

将相位补偿多项式拉伸到区间[-1,1]之间.利用Legendre多项式的正交性，将各阶系数作为遗传算法的编码可以解决编码的缠绕问题.

(2)描述相位变化的多项式系数n的选择：n越大，利用多项式建立的函数越接近真实的相位误差，但是n增大会导致优化对象复杂性的上升，不利于优化函数的收敛.

由振动的机理可以看出，越高频的分量其能量越小，也就是高阶能量是递减的.因此选取合适的n进行建模是比较重要的一个问题.

(3)适应度函数的选取：适应度函数是现有数据经过当前多项式相位补偿，压缩处理之后的结果进行量化评估的函数，对压缩结果的评估函数需要专门的研究，评估函数的计算量直接决定了算法的计算量和求解难度.需要适应度函数具备计算量小，函数性质简单等特点.

锐化函数[15]是常用的压缩评估算法之一，锐化函数这样定义：

(11)

锐化函数是评估能量集中程度的函数，能量越集中锐化函数值越高.但是当成像目标为块状目标时，锐化函数会存在过度补偿的问题.这是锐化函数的潜在的弊端.

为了能够解决对块状目标成像结果进行评估，在数据处理中采用压缩结果的差分数据的1-范数当做评价函数：

X(m)=D(m)-D(m-1)

(12)

(13)

其中symb=1，表示1-范数，X表示差分数据.使用该方法当做优化评价标准是基于未压缩完全的数据起伏比较大而压缩完全后起伏比较小的现象采用的.在仿真中，差分数据的1-范数表现出不错的性能，但是对实际数据的处理该评价方法并没有达到预期效果.差分数据的1-范数作为评价函数会在之后的研究工作中进行说明.

本文中采用锐化函数作为适应度函数.

在一定变化范围内对采集得到的数据的相位沿慢时间变化φ(tm)进行补偿后进行压缩，压缩结果最优时候就是当经过补偿的相位变化符合理想相位变化，相位变化与能量起伏相匹配，符合式(6)中相应的变化.在相位分布和能量起伏相匹配时进行压缩，压缩能量是最为集中的.所以可认为当补偿完全时，正是锐化函数值最大的时候，也就是适应度函数值最大的时候.

(4)先验知识的运用：根据振动机理，振动频率越高能量越小，在多项式中表现为项数越高则系数越小.由于Legendre多项式的性质，n阶Legendre多项式最高次项为n，所以Legendre多项式中也存在高阶系数小，低阶系数大的现象.

图2是一次成像试验中用14阶多项式补偿的压缩结果.

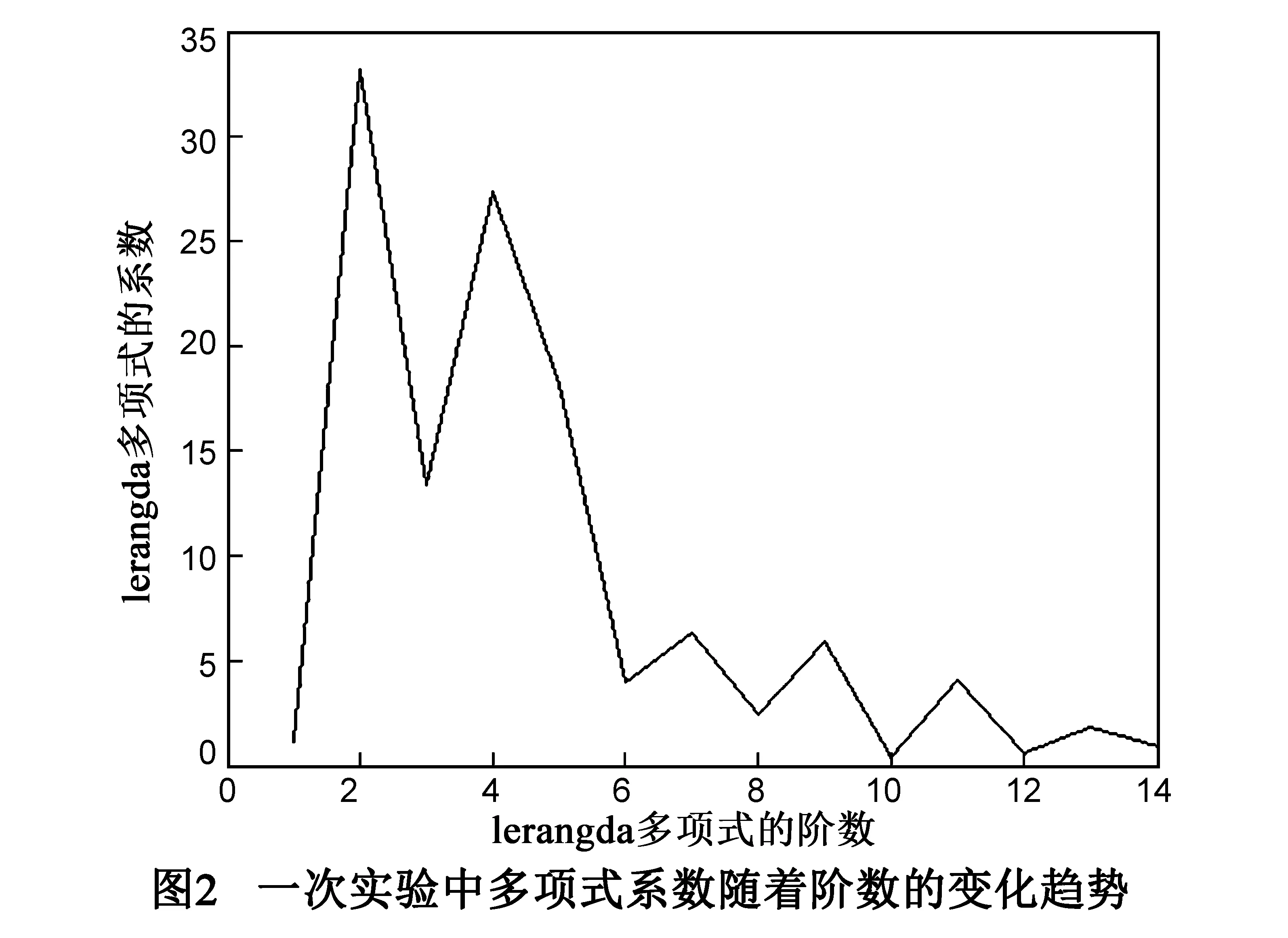
根据这个现象可以缩小系数的取值范围，提高搜索效率.缩小的倍数根据数据的信噪比进行估计，具体的范围需要通过经验估计.

数据是以矩阵形式被处理的，如果不考虑距离徙动，矩阵行对应同一距离门内沿慢时间变化的数据，矩阵列对应一个快时间内采集的数据.如果对每个距离门都用优化算法进行相位补偿非常耗时.式(8)可以看出，Rv(tm)带来的相位变化是独立于目标分布的，所以对不同距离门可以采用相同的相位误差补偿.挑选一个距离门内沿慢时间变化的一行数据，利用优化算法求出相位误差补偿的多项式系数，再分别补偿各个距离门的数据.

4 仿真结果分析

我们对优化算法对相位误差的补偿能力进行仿真分析，采用参数如下：飞行速度为60m/s，PRF为30kHz，添加的相位误差来源为航线偏移(图1)，来自于实测POS数据；机械振动在20Hz到2kHz之间随机产生，不同频率的振动之间具有相同的峰值加速度，按照国家军用标准关于环境适应性规定(GJB150.16-86)[16]，最大峰值加速度为2g，当设备安装有减震装置时，最高试验振动频率为500Hz[1].将最大峰值加速度设为20m/s2，平均分配到不同的频率中得到振动曲线，添加到数据中.目标分别采用单个目标和多个目标进行仿真.

图3是垂直于航向的振动曲线，将振动添加到两个单点目标数据生成，并且进行压缩.

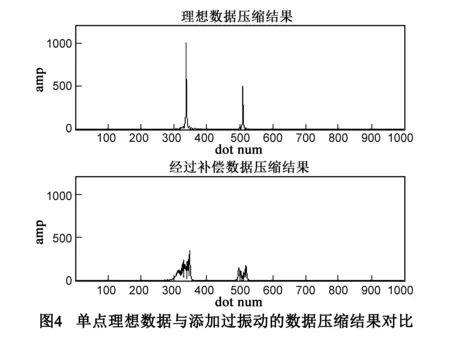
图4采用两个反射率不同的单点作为目标，其中上图表示理想数据压缩的结果，下图表示经过振动干扰的压缩结果，可以看到经过振动干扰之后压缩结果发生了很大的展宽.

采用优化算法对相位误差补偿，利用遗传算法按照上一章中提出的参数设计原则进行仿真，多项式阶数为9，经过150代的演化，得到最优解.压缩结果如图5所示.

可以看出，经过补偿之后压缩结果基本趋近于理想条件下的压缩，证明补偿充分.

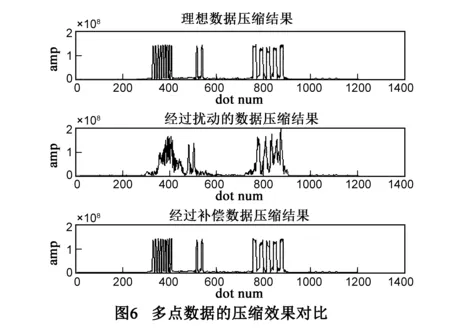
下面进行多目标仿真，这次进行遗传算法的参数和上次比有所调整，项数n取21，经过150代演化，获得局部最优解，用优化结果对相位进行补偿压缩之后得到结果如图6所示.

图5、图6分别为理想环境的压缩结果，经过扰动的压缩结果，以及经过扰动和优化算法补偿的压缩结果.经过优化算法的相位补偿可以修正带来的相位误差.经过补偿可以实现较为理想的压缩.

5 实验验证

采用基于相位编码体制的桌面成像系统，成像距离为1.76m，光斑大小为6mm，目标与镜头的相对运动速度为10cm/s，两个脉冲之间的采样间隔1ms.采集沿方位向变化的一行数据，加入平台机械振动.对结果运用优化算法对相位误差进行补偿实现压缩.目标设置如图7.

在方位向上分布有两个目标，相距大约为2cm，而目标宽度一个为1mm左右，另一个宽度是它的两倍.

对该目标进行压缩的结果如图8.

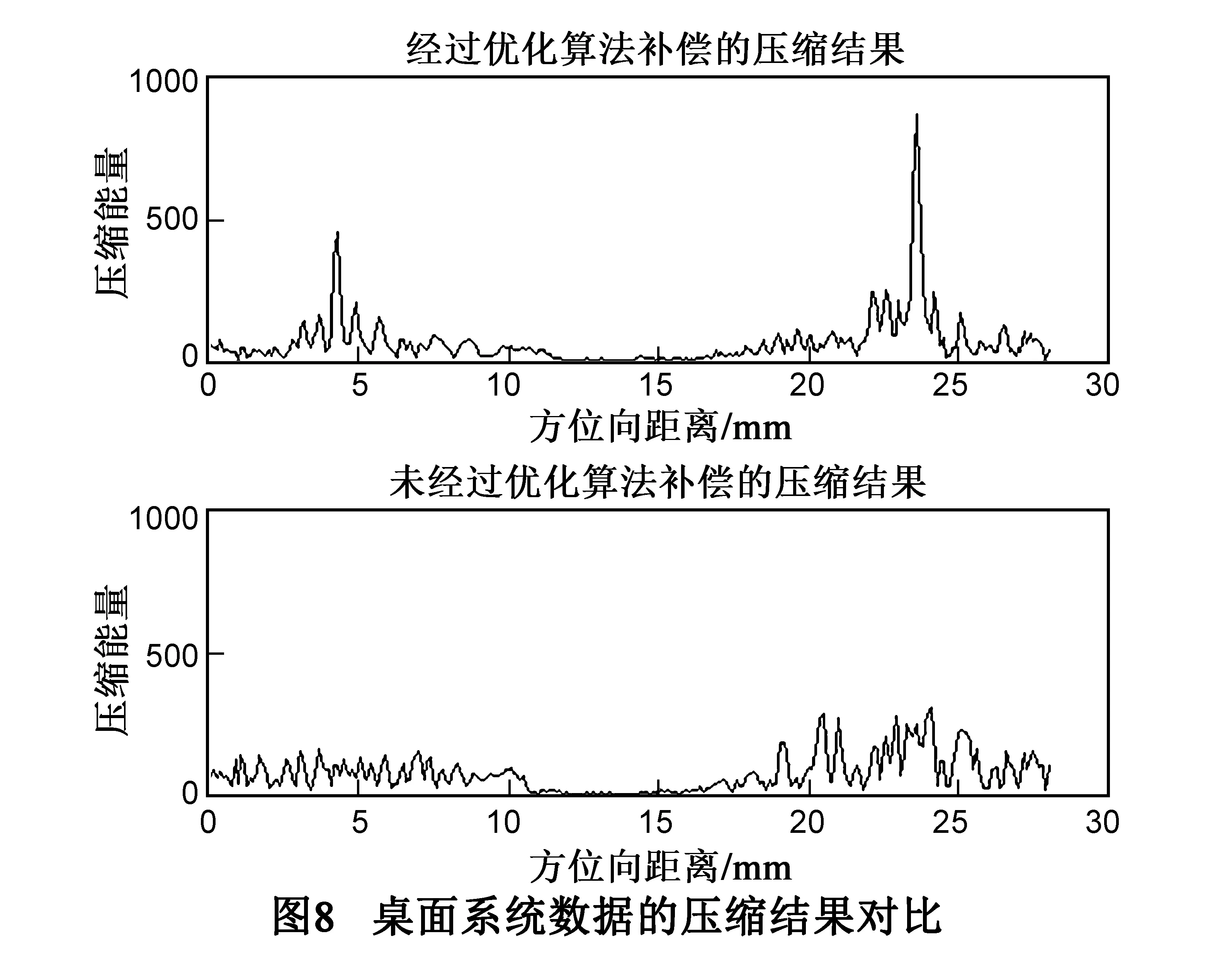
从图8可以对比看出，不使用优化算法对相位误差进行补偿，是无法压缩的；而使用优化算法可以明显看到两个目标的存在，一个宽度为700μm，一个宽度为1300μm，与实际目标设置也吻合.

6 结论

将振动带来的相位误差以多项式的形式进行分析，多项式系数作为优化目标.采用Legendre多项式系数当作遗传算法的编码；锐化函数作为相位补偿后压缩结果评估函数；合理估计多项式阶数；将这些参数带入到遗传算法中进行计算，是可以将需要补偿的相位误差多项式系数估计出来的.可以看到经过补偿后压缩结果接近理想结果.利用优化算法对相位误差进行补偿是值得继续研究的一个运动补偿算法方向.接下来进一步完善该算法需要从如下几个方面研究：(1)目标函数的选取：寻找比锐化函数更合适的压缩质量描述函数；(2)多项式数范围估计：需要在实际试验中进行统计和数据挖掘；(3)编码的选取：寻找较多项式更适合用有限项描述相位误差的数学模型.

[1]许楠，刘立人，鲁伟.合成孔径激光成像雷达距离向等延时的信号处理结构和算法[J].电子学报，2010,38(6):1405-1409.

XU Nan,LIU Li-ren,LU Wei.Signal processing construction and algorithm of range equal delay in SAIL[J].Acta Electronica Sinica,2010,38(6):1405-1409.(in Chinese)

[2]李增局，吴谨，刘国国,等.振动影响机载合成孔径雷达成像初步研究[J].光学学报，2010,30(4):994-1001.

Li Zengju,Wu Jin,Liu Guoguo,et al.Preliminary investigation on airborne SAL imaging with platform vibration[J].Acta Optica Sinica,2010,30(4):994-1001.(in Chinese)

[3]彭仁军，吴健，杨春平,等.用干涉法实现光学合成孔径技术[J].光学学报，2002,22(3)：355-359.

Peng Renjun,Wu jian,Yang Chunping,et al.Synthesizing aperture in optics with interferometric imaging[J].Acta Optica Sinica,2002,22(3):355-359.(in Chinese)

[4]洪光烈，郭亮.线振动对合成孔径激光雷达成像的影响[J].光学学报，2012,32(4):0428001

Hong Guang-Lie,Guo Liang.Analysis of effects of line vibration on imaging quality of synthetic aperture ladar[J].Acta Optica Sinica,2012,32(4):0428001.(in Chinese)

[5]Wahl D E,Eichel P H,Ghiglia D C,et al.Phase gradient autofocus-a robust tool for high resolution phase correction[J].IEEE Trans Aerosp Electron,Syst,1994,30(3):827-835.

[6]Brian W Krause,Joe Buck,Chris Ryan,et al.Synthetic aperture ladarflight demnstration[A].OSA/CLEO.IQEC[C].Washington,D C.:Quantum Electronics & Laser Science Conference,2011.1-2.

[7]Liu Liren.Coherent and incoherent synthetic-aperture imaging ladars and laboratory-space experimental demonstrations[J].Applied Optics,2013,52(4):579-599.

[8]Eddy A Stappaerts,E T Scharlemann.Differential synthetic aperture ladar[J].Optic Letters,2005,30(18):2385-2387.

[9]句赫，宋红军.相位梯度自聚焦算法在机载合成孔径雷达运动补偿中的应用[J].电子测量技术，2006,29(2)：19-20.

Jv He,Song Hongjun.Application of an improved PGA algorithm in SAR motion compensation[J].Electronic Measurement Technology,2006,29(2):19-20.(in Chinese)

[10]李道京，张清娟，刘波,等.机载合成孔径激光雷达关键技术和实现方案分析[J].雷达学报,2013,2(2):143-151.

Li Dao-jing,Zhang Qing-juan,Liu Bo,et al.Key Technology and implementation scheme analysis of air-borne synthetic aperture ladar[J].Journal of Radars,2013,2(2):143-151.(in Chinese)

[11]保铮，邢孟道，王彤.雷达成像技术[M].北京：电子工业出版社，2005.192-193.

[12]陈行勇,刘永祥,姜卫东,等.微动目标合成距离向数学分析[J].电子学报,2007,35(3):585-589.

Chen Hang-yong,Liu Yong-xiang,Jiang Wei-dong,et al.Mathematic of synthesizing range profile of target with micro-motion[J].Acta Electronica Sinica,2007,35(3):585-589.(in Chinese)

[13]葛继科，邱玉辉，吴春明,等.遗传算法研究综述[J].计算机应用研究,2008,25(10):2911-2916.

Ge Jike,Qiu Yuhui,Wu Chunming,et al.Summarization of research on genetic algorithm[J].Application Research of Computers，2008,25(10):2911-2916.(in Chinese)

[14]季孝达，薛兴恒，陆英.数学物理方程[M].北京：科学出版社,2005.134-139.

[15]Walter R Buell,Nicholas J Marechal,Joseph R Buck,et al.Demonstration of synthetic imaging ladar[A].Proc SPIE[C].New York:Defense & Security,2005.5791:152-166.

[16]GJB 150.16-86中国人民解放军总装备部国家军用标准环境I[S].

张鸿翼 男，1988年生于山西太原，中国科学院大学上海技术物理研究所在读博士，研究方向为合成孔径激光雷达.

E-mail：zhanghongyi3432@sina.com

李 飞 男，1988年生于河北石家庄，中国科学院大学上海技术物理研究所在读博士，研究方向为合成孔径激光雷达.

E-mail：stonehood@126.com

Research on the Phase Error Compensation in Synthetic Aperture Ladar by Using Optimization Algorithm

ZHANG Hong-yi,LI Fei,XU Wei-ming,SHU Rong

(KeyLaboratoryofSpaceActiveElectronic-OpticalSystems,ShanghaiInstituteofTechnicalPhysics,ChineseAcademyofSciences,Shanghai200083,China)

In the field of remote sensing,the platform vibration is one of the important problems of synthetic aperture ladar(SAL).There is no efficient method in compensating the platform vibration of SAL currently.The platform vibration effects the phase of the received data.By analyzing the mechanism of platform vibration,the phase error caused by platform vibration can be described by polynomial function.The vibration is compensated by optimization algorithm which optimizes the polynomial coefficients based on this conversion model.In optimization process,proper object function is needed and the phase of received data is compensated by optimization result,then the compensated data is compressed by matched filter.By simulation and experimental result,the conclusion is the better result of compression can be achieved after compensate the phase error by using the optimization algorithm.The research has offered candidate technology to platform vibration compensation.

remote sensing; phase error; vibration compensation; optimization algorithm; polynomial

2014-11-15;

2015-11-12;责任编辑：蓝红杰

国家863高技术研究发展计划(No.2014AA7100012)

O436

A

0372-2112 (2016)09-2100-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.09.012