可抛掷移动机器人上下楼梯机构设计及仿真
2016-11-22张世隆施家栋王建中朵英贤
张世隆, 施家栋, 王建中, 朵英贤
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081 )
可抛掷移动机器人上下楼梯机构设计及仿真
张世隆, 施家栋, 王建中, 朵英贤
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081 )
针对可抛掷移动机器人体积小、质量轻,便于携带和快速部署,受自身体积限制,目前可抛掷移动机器人均不具备上下楼梯功能的问题. 提出一种适用于可抛掷机器人的垂直上下楼梯机构,通常情况下,仍以抛投的形式进入工作环境,当需要进行多楼层搜索时,加装上下楼梯模块,而后以遥控模式驶入工作区. 针对该机构进行控制方案设计,并基于RecurDyn及Simulink软件建立机械-控制系统模型,对机器人不同初始姿态的情况下进行上下楼梯动力学仿真. 结果表明,可抛掷移动机器人能够实现自主上下楼梯功能,上下楼梯过程动作平稳. 该机构解决了机器人上下楼梯性能与机器人体积重量之间的矛盾.
可抛掷移动机器人; 自主上下楼梯; 机械-控制系统模型; 动力学仿真
微小型地面移动机器人能在复杂、狭窄、危险区域工作,广泛应用于侦查、搜救、探测等领域. 便携性、越障性能是此类机器人的重要指标,对机器人的体积、质量有严格要求[1]. 可抛掷机器人体积小、质量轻,便于单兵携带,可通过人工抛掷、弹射、空投等方式进入工作区从而达到快速部署的目的.
可抛掷机器人按照机器人本体结构类型主要分为两类. 第1类主要包括哑铃状两轮结构、球形结构及球形可变形结构[2]. 美国明尼苏达大学研制了Scout机器人及弹射平台Ranger. Scout机器人为哑铃状两轮机器人,Ranger负责运载和弹射Scout,以弹簧弹射的方式部署10个Scout,将Scout的活动范围扩大到20 km. 卡内基·梅隆大学D.O’Halloran等[3]研制了一种能够承受较大跌落冲击的两轮机器人,其减震措施主要为充气式橡胶减震轮、悬挂底盘系统. 北京理工大学、北京航空航天大学、国防科技大学等机构分别对2轮式、球形可变形机器人进行了研究,并研制出多款机器人样机[4-6]. 以上机器人共同特征是移动时呈哑铃状结构,重量一般在1 kg以内,其自身抗冲击能力强,但机动性、复杂地面的通过性能较差,部署方式以抛投、弹射为主. 第2类可抛掷机器人采用轮式、履带式底盘结构,质量通常在5 kg以内,可短距离抛掷使用. 美国Irobot公司开发的可抛投机器人110 FirstLook采用履带式结构,底盘前部左右各有1个摆臂,用于翻转车体以及辅助越障. 美国卡内基·梅隆大学机器人技术研究所联合美国海军研究实验室共同研制Dragon Runner机器人系统,可携带音频、视频传感器等多种载荷.
本文提出一种适用于可抛掷机器人的上下楼梯机构,通常情况下,仍以抛投的形式进入工作环境;当目标所在楼层区域不确定,需进行多个楼层搜寻时,则在机器人进入工作环境之前,加装上下楼梯模块,而后以人工遥控模式驶入工作区域. 这使得可抛掷机器人在特殊使用条件下具备上下楼梯功能.
1 结构方案
基于机器人尺寸小、越障性能强的指导思想,提出一种垂直上下楼梯动作方案:将每一级台阶视为一个障碍物,机器人首先依靠支架将自身重心抬升至楼梯台阶高度,而后将重心向前推送至台阶面上,最后将支架收回.
为实现上述动作方案,在普通履带式机器人的基础上,设计一套爬楼梯支架组件. 如图1所示,爬楼梯支架组件包括车体两侧的升降杆、升降电机、横梁、导轨、推送电机以及连接块. 其中横梁与导轨固联,横梁与升降杆可在竖直方向上相对运动;推送电机可在导轨内前后运动;连接块与推送电机、车体相连,其包含机械、电子接口.
车体前端有摄像头、红外测距传感器,用于图像采集和前方测距;此外,车体底部安装2个红外测距传感器,用于测量车体与地面之间的距离.
上楼梯过程描述:① 行驶至台阶附近,借助摄像头、红外传感器,自动靠近台阶并对正(图2(a));② 升降电机将车体抬升,此时车体上升至台阶高度(图2(b));③ 推送电机将车体向前推送,同时驱动轮带动履带运动,使车体前进速度与履带运动线速度相等(图2(c));④升降电机将爬楼支架组件抬升(图2(d));⑤ 推送电机将爬楼支架收回原位,在该过程中履带可同时运动(图2(e)),至此爬升第1级台阶结束. 若攀越第2级台阶,则重复以上过程.
下楼梯过程与上楼梯相反,按照图2(a)~2(e)所示依次执行动作,不同之处为,图2(e)所示状态下,需进行台阶边缘对正及台阶高度探测.
为便于上下楼梯,现有机器人多采用履带式结构. 在上下楼梯过程中,每条主履带与台阶边缘至少有2个接触点,这样可以保证机器人姿态稳定且与台阶具有较强的附着力. 这对履带以及机器人自身长度有最低要求. 例如,相邻两台阶边缘的距离为S,则机器人履带的有效长度应不小于2S[7],如图3所示. 采用垂直爬楼梯方案,爬楼梯支架的高度大于台阶的高度,底盘的总长度小于台阶的宽度,使得机器人可在台阶上灵活运动. 该结构方案可使机器人体积大幅度减小.
2 虚拟样机模型建立
2.1 关键状态分析
上述上下楼梯方案是否可行,关键之处为:①重心位置是否可以满足稳定性要求,即在将爬楼机制收回的过程中(对应图2(c)至图2(d)),应避免发生机器人从台阶面上向后翻倒的现象;②整体尺寸、质量是否满足可抛掷移动机器人的设计要求. 为便于单兵携带和抛掷,机器人质量不宜过大;同时,为保证机器人在台阶面上的稳定性,要求机器人车体的长度不大于台阶面的宽度.
对图2(d)所处状态受力分析如图4所示. 假设导轨的前端与台阶竖直面对齐,车体重心距台阶边缘l1,支架组件重心距台阶边缘l2,则m1gl1-m2gl2>0.
机器人车体向前推送的最大距离为l,车体重心距车体前端l0,则l1=l-l0,上式可化为
(1)
式(1)即为机器人不向后翻倒的条件.
两个抬升电机车体向上抬升过程中,需要电机提供较大的力矩,对该过程进行受力分析. 假定传动方式采用齿轮齿条,其中齿轮安装在滑块上,受力状态如图5所示.
其中G为车体、电机组件、横梁以及抬升电机组件的重量,r为齿轮半径. 匀速上升阶段,单个抬升电机及减速器输出力矩为T,则升降杆对齿轮竖直方向的支反力F=T/r. 竖直方向上合力为0.
(2)
式中f为滑块与升降杆之间的摩擦力. 将齿轮及滑块视为整体,将车体重力简化为一个过A点的力及力偶,单侧抬升电机组件的受力图简化为图5(b),其中,力偶M=GL.
(3)
(4)
式中:FN为滑块与升降杆之间的正压力;u为摩擦因数. 关于点A力矩平衡,可得
(5)
要求车体向上抬升的速度为v,则对应电机减速器输出轴转速w=v/r. 单个电机功率用P0表示,则车体向上抬升所需功率为P=2P0=2Tw.
初选d=30mm,r=10mm,要求车体抬升速度v=50mm/s. 假定G=30N,车体长度L=240mm,重心位置距升降杆的距离约为L/4,升降杆与滑块采用钢质构件,摩擦因数u=0.1. 可得
T=240 mN·m;w=47.75 rad/s;P0=1.2 W.
即要求单个电机组件输出扭矩大于240mN·m,转速47.75r/min,电机输出功率大于1.2W. 选取MAXONRE16 3.2W电机及其对应减速器GP16A,减速比84∶1,主要参数如表1所示,其中效率、质量数据含减速器在内.
行驶电机主要依据平地行驶速度及爬坡角度确定,选择型号MAXONRE16 4.5W及对应减速器GP16A,减速比157∶1. 选型设计过程不再赘述,具体参数见表1.

表1 电机主要参数
2.2 建立虚拟样机
对于普通室内楼梯而言,台阶竖直面高度120~175 mm,台阶水平面宽度260~340 mm. 此处建立3级楼梯模型,第1级台阶高150 mm,宽300 mm;第2级台阶高150 mm,宽260 mm;第3级台阶高180 mm. 根据以上主要尺寸及3.1节受力分析结果,进行机器人总体尺寸设计,并对电机、电池、摄像头、红外传感器等构件初步选型,得机器人组件主要结构参数如表2所示.

表2 抛投式移动机器人组件尺寸及质量
基于多体系统动力学软件RecurDyn[8]建立虚拟样机,如图6所示,其中左侧为机器人前端. 说明:① 摄像头、红外传感器、电池等器件外形省略,其质量附加在机器人车体上;② 为降低模型复杂程度,将履带替换为车轮,车轮与地面的摩擦因数设为0.8;③ 其余接触、运动副摩擦因数为0.1.
3 上单级台阶动力学仿真
机器人上、下楼梯过程动作相反,在此仅模拟机器人上楼梯过程,以验证动作方案是否可行.
利用step函数[8]对行驶电机、抬升电机、推送电机进行速度控制,设定仿真类型为dynamic,仿真时间40 s,分析步为1 000.
仿真结果:机器人能够爬上第1级楼梯. 上楼梯过程如图7所示,其中红色实线为车体质心轨迹,0~3 s车体向楼梯靠近,3~10 s车体抬升至1级楼梯高度,10~20 s车体向前推送,20~37 s将爬楼支架收回.
从图7中可以看出,借助于该爬楼支架机构,可抛掷移动机器人能够上1级楼梯,这验证了机构方案的可行性. 从机器人车体的质心轨迹可以看出,机器人爬楼动作平稳、可靠.
机器人运动涉及5个电机,其中2个行驶电机、2个抬升电机所需功率较大,1个推送电机功率较小. 0~10 s内,机器人执行平地行驶、车体抬升动作,该过程中行驶电机、抬升电机功耗最大. 提取0~10 s内左侧行驶电机、左侧抬升电机的输出扭矩及电机转速,如图8、图9所示.
从图8可知,行驶电机组件输出扭矩约为300 mN·m,最大输出扭矩418 mN·m;车体抬升过程中,抬升电机组件输出扭矩约为150 mN·m,最大输出扭矩为216 mN·m. 由图9可知,上楼梯过程中,行驶电机组件最大转速3 rad/s,结合图8可知,电机达最大转速时对应最大输出功率1.25 W;抬升电机组件最大转速3.34 rad/s,对应最大输出功率0.72 W. 所需功率、转矩、转速均在所选电机参数范围内,能够满足抛投式移动机器人上下楼梯机构的需求.
4 控制策略
机器人在爬楼梯过程中,摄像头视野有限,操作者无法准确判断机器人与台阶相对位置. 因此该机器人需其具备自主上下楼梯功能以提高爬楼梯效率. 红外测距技术具有设备体积小、灵敏度高等特点,机器人车体前端、底部分别加装2个红外传感器,如图10所示,前端传感器用于探测距楼梯竖直面距离,底部传感器用于探测车体离地距离.
上楼梯程序流程如图11所示,DL,DR分别表示车体前端左、右红外传感器测得的距离信息,DBL,DBR分别表示车体底部左、右红外传感器测得的距离信息. 启动爬楼梯程序后,车体向台阶靠近,根据DL,DR值调整电机转速与楼梯竖直面对正;当左右两侧的距离值处于设定阈值范围,对正任务完成,进入车体抬升环节;当车体前端测距值由低变高时(如:由小于20 mm变为大于100 mm),判定为传感器高度超出台阶平面,待车体继续抬半个车体厚度时,记录抬升电机旋转过的角度θ0,此时推送电机启动,进入车体向前推送环节;在车体向前推送的过程中,行驶电机正转,使得主动轮的线速度与车体向前推送的速度相同;当车体向前推送距离达设定值L0,此时整车重心已移动至台阶面上,抬升电机反转,将升降杆收回;抬升电机反转角度值达θ0,升降杆运动到位,推送电机反转将爬楼支架收回,第1级台阶攀爬结束. 机器人恢复向前行驶状态,靠近并攀爬第2级台阶. 当机器人处于“向前行驶”状态,且探测到前方距离大于300 mm时,判定为机器人已爬到顶层阶梯,上楼梯程序终止.
下楼梯程序流程与上楼梯基本相反,如图12所示,主要不同之处在于:① 启动下楼梯程序后,车体向后行驶,当测得DBL,DBR数值大于某界限时,认为到达台阶边缘,进入机器人与台阶边缘对正环节,并记录测得的DBL,DBR值(台阶高度信息);② 下第1级楼梯结束后,机器人恢复向后行驶状态,若向后行驶300 mm仍未到达台阶边缘,则认为以达到楼梯底层台阶,下楼梯程序终止.
5 上下多级楼梯动力学仿真
5.1 机械-控制系统建模
基于多体动力学软件Recurdyn及动态控制软件Simulink,建立机械-控制系统联合仿真模型,如图13所示. 其中Recurdyn机械系统模型,包含了机器人本体、驱动系统、执行机构等;Simulink控制系统模型包括控制器和驱动器两部分;通过输入变量Plant Output(简称POUT)、输出变量Plant Input(简称PIN)和M文件(M-file)将机械模型和控制模型关联起来.
图13中,DL,DR,DBL,DBR分别表示车体前端左、右红外传感器及车体底部左、右红外传感器所测的距离信息,DF表示推送电机距导轨前端距离,vL,vR,vBL,vBR,vF分别表示左行、右行驶电机、左、右抬升电机及推送电机的转速指令. 控制器以图11、图12所示的程序流程图为核心,借助Simulink的状态机(StateFlow)模块编程实现.
5.2 仿真实验及结果分析
为了验证该机械结构及控制策略的合理性,进行多工况仿真实验. 实验分上楼梯、下楼梯2种任务;依据机器人初始位置,分为与楼梯对正、与楼梯呈一定角度2种情况.
机器人前轮轴线与楼梯竖直面的夹角记为α,当α=0°时,机器人处于对正状态. 机器人距第一级楼梯的初始距离记为D,台阶尺寸如3.2节所述. 以Simulink为主程序,进行Recurdyn/Simulink实时联合仿真. 实验条件与结果如表3所示.
实验1、实验2表明,基于该控制方案,机器人能够完成自主上下楼梯动作. 实验3、实验4表明,机器人与楼梯呈一定夹角的情况下,可自动检测对正,并成功完成自主上下楼梯动作.
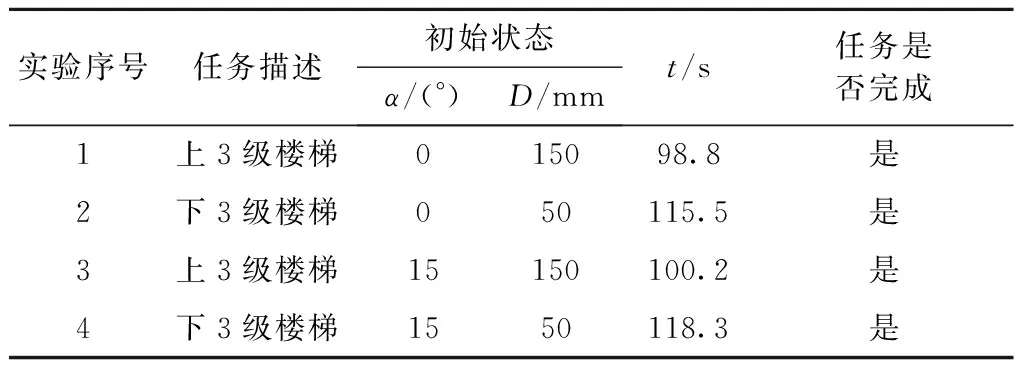
表3 上下3级楼梯实验结果
以上述实验2为例,观测机器人自主上楼梯过程. 其中机器人车体、横梁、升降杆的重心高度随时间变化曲线如图14所示. 图15为上楼梯过程截图.
6 结 论
基于抛投式机器人的体积小的结构特点,提出了一种垂直爬楼梯方案,并据此设计了上下楼梯机构及相应的控制策略. 基于RecuDyn/Simulink建立机器人机械-控制系统模型并进行仿真实验,结果验证了机械结构的可行性及控制策略的合理性.
在未来的的工作将研制机器人物理样机,并对以下方面重点研究:分析并验证传感器误差对机器人感知性能鲁棒性的影响;基于多电机协同控制技术,解决左右抬升电机同步性问题.
[1] Richter L, Schilling K, Bernasconi M C, et al. Mobile micro-robots for scientific instrument deployment on planets[J]. Robotics and Autonomous Systems, 1998(23):107-115.
[2] 孙明磊,王启伟,张融,等.一种便携式可伸缩球型抛掷侦察机器人:中国,CN 102267505 B[P].2012-11-07.
Sun Minglei, Wang Qiwei, Zhang Rong, et al. A portable spherical throwable reconnaissance robot: China,CN 102267505 B[P]. 2012-11-07.(in Chinese)
[3] O’Halloran D,Wolf A, Choset H. Design of a high-impact survivable robot[C]∥Proceedings of the 2004 IEEE International Conference on Robotics & Automation. New Orleans, USA : [s.n.], 2000:3551-3558.
[4] Zhang Liancun, Huang Qiang, Li Yue, et al. Research and development of throwable miniature reconnaissance robot[C]∥Proceedings of 2012 IEEE International Conference on Mechatronics and Automation. Chengdu, China:[s.n.], 2012:1254-1259.
[5] Gao Hengrui, Bi Shusheng, Zhang Rong, et al. The design of a throwable two-wheeled reconnaissance robot[C]∥Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics. Guangzhou, China:[s.n.], 2012: 2150-2155.
[6] 罗自荣,尚建忠,丛楠,等.可抛掷多运动态球型机器人移动机构[J].机械设计,2009(9):30-33.
Luo Zirong, Shang Jianzhong, Cong Nan, et al. Moving mechanism of polymorphic spherical throwable robot[J]. Journal of Machine Design, 2009(9):30-33.(in Chinese)
[7] 陈晓东.警用机器人[M].北京:科学出版社,2008:18-20,75.
Chen Xiaodong. Police robot[M]. Beijing: Science Press, 2008:18-20,75.(in Chinese)
[8] 张湝渭,彭斌彬.RecurDyn多体系统优化仿真技术[M].1版.北京:清华大学出版社,2010:298-309.
Zhang Jiewei, Peng Binbin. RecurDyn molti-body system optimization technology[M]. 1st ed. Beijing: Tsinghua University Press, 2010:298-309. (in Chinese)
(责任编辑:刘雨)
Design and Simulation of Throwable Mobile Robot Stair-Climbing Mechanism
ZHANG Shi-long, SHI Jia-dong, WANG Jian-zhong, DUO Ying-xian
(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
Characterizing small and light, throwable mobile robots are portable and easy to be deployed, so they are widely used in investigation, rescue, detecting and so on. But throwable mobile robots could not climb up stairs for their small dimensions. In this paper,a stair-climbing mechanism was presented for throwable mobile robots. In common cases, the robot still was deployed by throwing. The stair-climbing mechanism only was equipped when the robot had to work on different floors, and the robot must be controlled remotely into work space. A control strategy was designed corresponding to that structure, and a mechanism-control system model was established based on Recurdyn and Matlab/Simulink software. The results of virtual stair-climbing experiments show that, the robot can autonomously climb stairs up and down steadily with this mechanism. This mechanism can solve the contradiction of throwable robots' dimensions and their stair-climbing capability.
throwable mobile robots; autonomous stair-climbing; mechanism-control system model; dynamics simulation
2014-11-06
长江学者和创新团队发展计划(IRT1208)
张世隆(1986—),男,博士生,E-mail:xiaoshidejia@126.com.
施家栋(1982—),男,博士,讲师,E-mail:sjd215@bit.edu.cn.
TP 242
A
1001-0645(2016)06-0574-07
10.15918/j.tbit1001-0645.2016.06.005
