改进的小波阈值去噪方法在MEMS陀螺上的应用

吴锐， 周守东

(安徽工业经济职业技术学院, 合肥230051)



改进的小波阈值去噪方法在MEMS陀螺上的应用

吴锐， 周守东

(安徽工业经济职业技术学院, 合肥230051)

针对MEMS陀螺由于结构瑕疵和信号处理技术的不足而导致存在较大的随机误差，采用改进的小波阈值去噪方法以提高MEMS陀螺测量精度。通过对软阈值函数和硬阈值函数的缺陷进行分析，设计了改进的阈值函数。改进的阈值函数相对于硬阈值函数具有连续性的优势，相对于软阈值函数可以减小常值误差。根据不同阈值去噪方案在陀螺静态数据上的去噪效果，确定了最终的阈值去噪方案。将此方案应用在MEMS陀螺的动静态数据中，实验结果表明：MEMS陀螺输出信号的标准差减小了一个数量级，平均值更加接近真实值，所提出的采用改进的小波阀值去噪方法取得了很好的去噪效果。

小波阈值降噪；改进的阈值函数；MEMS陀螺；随机误差

引言

随着微电子技术和集成电路的发展，MEMS陀螺朝着小型化、低功耗、高可靠性的方向发展。MEMS陀螺在自动化、航空航天和武器制导等军民用领域得到广泛应用[1-4]。但是由于结构的瑕疵和信号处理技术的不足，MEMS陀螺的噪声和漂移很大，这是阻碍其实用的最大因素。噪声覆盖了陀螺输出的真实特性，所以必须采取措施提高信噪比，为MEMS的随机漂移建模和补偿打下基础[5-8]。

陀螺仪在惯性导航组件中起到传感器的作用，敏感平台的转动趋势，然后通过平台稳定系统将平台稳定在惯性空间中，所以陀螺的精度决定了导航的精度。相对于转子陀螺、光学陀螺，MEMS陀螺仪具有体积小、成本低、功耗低等诸多优势，近几年也随着集成能力的进步而获得了较大发展。但是由于生产水平有限，导致目前MEMS陀螺的精度偏低，这是限制其广泛进行应用的最主要因素[9-12]。因此在当前生产水平下，寻找提高MEMS陀螺精度的方法非常必要。MEMS陀螺的噪声主要是随机噪声，它由外界环境的不确定因素引起的。简单的去噪方法难以将噪声从信号中滤除掉，最基本的信号处理方法是傅里叶变换，但是傅里叶变换是全局变换，无法反应出信号局部的频率特点[4]。常使用小波变换时频域分析的优势来解决这一问题。小波分析窗的尺寸固定但形状可变，根据时域中样本频率的不同来调整采样步长。小波变换的去噪方法中，小波阈值去噪具有相对简单、运算量小等特点，可以获得很好的去噪效果[7,13-14]。

本文提出了改进的小波阈值函数，并设计了相应的小波阈值降噪方案，并用此方法来处理MEMS陀螺动静态条件下的输出信号，取得了很好的去噪效果。

1 MEMS陀螺的Allan方差分析

Allan方差法首先应用于原子钟的频率波动特性分析，由于陀螺的随机误差与原子钟非常相近，因此Allan方差法被IEEE推荐为陀螺随机误差辨识的标准方法。Allan方差可以将陀螺随机误差分为五类：量化噪声(Q)、角度随机游走(N)、零偏不稳定性(B)、角速率随机游走(K)和速率斜坡(R)。Allan方差分析就是辨识出这五类误差的大小[5]。

将恒温箱温度设置为23 ℃，MEMS陀螺在恒温箱内保温30 min后采集陀螺输出，采样频率为1000 Hz，采样时间为1 h，陀螺Allan方差分析结果见表1。

表1 MEMS陀螺X轴的Allan方差分析

从表1中可以看出，在X轴的随机误差中，量化噪声和角度随机游走是其主要组成部分，另外两个轴也具有相同的结论。

2 小波阈值降噪

2.1 小波阈值的选取原则

根据文献[6]可知，噪声信号的数学模型为：

s(k)=f(k)+ε·e(k) k=1,2,…,n-1

(1)

式中：s(k)为含噪信号，f(k)为有用信号，e(k)为噪声信号。对信号s(k)进行小波变换，可以将此信号分为有用信号f(k)和噪声信号e(k)。工程实践表明，噪声信号是高频信号，而有用信号是相对稳定的低频信号。因此在小波变换中它们的统计特性不同，有用信号的小波变换幅值较大，而噪声信号的小波变换幅值较小。因此可以找到合适的阈值，当小波分解系数大于阈值时，认为此部分为有用信号；当小波分解系数小于阈值时，认为此部分为噪声信号，将此系数置0。然后通过小波重构获得降噪后的信号。小波阈值降噪可以具体为以下三步：

(1) 原始信号的小波分解。基于信号的特性选择小波函数和分解阶数，对信号进行小波分解。

(2) 通过高频小波系数量化阈值或阈值函数，按照给定的规则将噪声信号系数置0。

(3) 将处理后放入信号进行重构获得滤波后的信号。

2.2 选择小波基函数和分解层次

在小波变换中，小波函数有很多种，分析同一个问题时所使用的小波基函数不同，结果也就不同，因此选择小波基函数非常重要。当前主要通过处理信号的误差和结果确定小波函数，所选基函数要具有规则、消失矩、对称等特点。通过比较不同的小波函数，选取Coif2为基小波，分解层次为9。

2.3 小波阈值的选取和量化

在小波阈值降噪的过程中，最重要的就是阈值的选择和量化，阈值的选取直接决定了降噪的质量。

对于阈值的选择，常用的有两种方法：一是基于信噪比选择阈值，二是基于信号的无偏风险估计。阈值主要包括固定阈值(Sqtwoolog)、Stein无偏似然估计(Rigrsure)、Heursure阈值(Heursure)、Minimax阈值(Minimax)。本文根据不同阈值的去噪效果来决定阈值的选取。

选取小波阈值以后，重要的事情是阈值函数的使用和阈值的量化。目前常用的Donoho硬阈值函数为:

(2)

软阈值函数为：

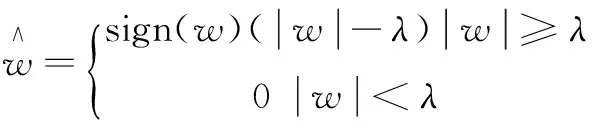
(3)

两种阈值函数在直线上的应用结果如图1 所示。

图1 展示了当阈值为0.4 时，软阈值和硬阈值在直线上的应用效果。从图中可以看出，硬阈值函数在λ和-λ点不连贯，这会导致信号滤波后的突变，这是硬阈值函数派生出的计算问题。而且硬阈值函数只将比阈值小的系数置0，而不处理比阈值大的系数，这种方法过于绝对。虽然软阈值的连续性很好，但是使用软阈值函数降噪后，去噪后的信号和原始信号存在常值偏差。

为了克服硬阈值函数不连续和软阈值函数存在常值偏差的缺陷，本文提出了改进的软阈值函数。首先将软阈值函数(3)改写为

(4)

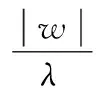
(5)

图2 三个阈值函数在直线上的应用

从图2中以看出，改进的阈值函数相对于硬阈值函数具有连续性的优势，相对于软阈值函数减小了固定偏差。因此，改进的阈值函数相对于软阈值函数和硬阈值函数都具有进步意义。

3 小波阈值方案的确定和验证

3.1 小波阈值降噪方案的确定

为了确定最终的小波阈值降噪方案，将上文中提到的小波阈值估计方法应用到三种阈值函数中，对陀螺的静态输出数据进行小波阈值降噪，来对比各种方案下的降噪效果，计算滤波后数据的标准差，以此为标准来确定最终的滤波方案。数据处理的结果见表2。

通过表2中数据的对比，可以看出小波阈值为Birge-Massart准则确定的阈值、阈值函数使用改进的阈值函数时，取得了最好的去噪效果。

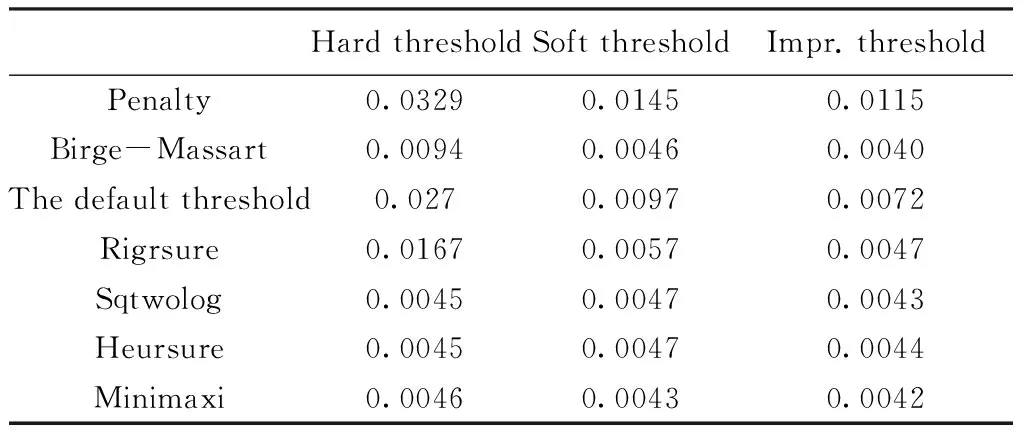
表2 各种阈值方案的去噪结果

终上所述，最终选取Coif2为小波函数，对原始信号分解到9阶，Birge-Massart准则为阈值评估准则，改进的阈值函数为最终使用的阈值函数。此方案即为最终设计的降噪方案。

3.2 小波阈值降噪验证和信号重建

以上的阈值降噪方案是通过对陀螺静态数据的分析获得的，为了验证此降噪方案的有效性，将此方案分别应用在其他静态数据和动态数据中。动态测试在常温条件下进行，将陀螺固定在转台上，使其输入轴平行于转台轴，将转台转速设置为10 °/s，等转速稳定以后开始测试数据。设计的阈值降噪方案在动静态数据中的去噪效果如图3 所示。

图3 动静态数据的去噪效果

下面从平均值和标准差两个方面对比降噪前后的效果，具体数据见表3。

表3 降噪前后数据的对比

从图3 可以看出，不管动态数据还是静态数据，经过小波降噪，数据的稳定性都有了很大提高。从表3中可以看出，滤波后的平均值也更加接近真实值，标准差也降低了一个数量级。通过上面的分析可以看出，本文设计的阈值降噪方案应用在MEMS陀螺的动静态数据中，不仅极大地提高了数据稳定性，也使数据平均值更加接近真实值，证明了此降噪方案的有效性。

4 结束语

本文首先分析了软阈值函数和硬阈值函数的缺陷，然后设计了改进的阈值函数。改进的阈值函数相对于硬阈值函数具有连续性的优势，相对于软阈值函数可以减小常值误差。根据不同阈值去噪方案在陀螺静态数据上的去噪效果，确定了最终的阈值去噪方案。将此方案应用在MEMS陀螺的动静态数据中，将输出信号的标准差减小了一个数量级，平均值更加接近真实值，取得了很好的去噪效果。

[1] 王新龙，李娜.MEMS陀螺随机误差的建模与分析[J].北京航空航天大学学报,2012,38(2):170-174.

[2] 王伟,杜东贞,周佳欣,等.MEMS三轴陀螺仪中不匹配干扰抑制方法[J].系统工程与电子技术,2016,38(7):1638-1643.

[3] 陈殿生，邵志浩，雷旭升,等.MEMS陀螺仪随机误差滤波[J].北京航空航天大学学报,2009,35(2):246-250.[4] 宋丽君,秦永元,杨鹏翔.小波阈值去噪法在MEMS陀螺仪信号降噪中的应用[J].测试技术学报,2009,23(1):33-36.

[5] XUE L,JIANG C Y,CHANG H L,et al.A novel Kalman filter for combining outputs of MEMS gyroscope array[J].Measurement,2012,45(4):745-754.

[6] 吴焕铭,尹韬,杨海钢,等.基于双通道解调相位校准技术的MEMS 陀螺仪接口电路芯片[J].中国惯性技术学报,2015,23(6):806-810.

[7] 高伟伟,王广龙,高凤岐,等.一种基于DAVAR的FOG随机信号处理新方法[J].解放军理工大学学报:自然科学版,2014,15(4):330-334.

[8] 何鲲鹏,程万娟,高延滨,等.虚拟陀螺技术在MEMS惯性导航系统中的应用[J].哈尔滨工业大学学报,2009,30(10):1123-1128.

[9] CHANG H,XUE L,QIN W,et al.An integrated MEMS gyroscope array with higher accuracy output[J].Sensors,2008,8(4):2886-2899.

[10] 吉训生,王寿荣.硅微陀螺阵列信号处理研究[J].宇航学报,2009,30(1):235-239.

[11] 皱学锋,卢新艳.基于Allan方差的MEMS陀螺仪性能评价方法[J].微纳电子技术,2010,47(8):490-493.[12] 于丽杰,高宗余.MEMS传感器随机误差分析[J].传感器与微系统,2012,31(3):63-65.

[13] 程旭维,汤霞清,黄湘远.基于#1理论方差的光学陀螺长期随机误差分析[J].中国激光,2014,41(10):10005003.1 -10005003.8.

[14] RILEY W J.Techniques for Frequency Stability Analysis[C]//Proceeding of IEEE International Frequency Control Symposium,Tampa,FL,May 4-8,2003:1-10.

Application of Improved Wavelet Threshold Denoising Method for MEMS Gyroscop

WURui，ZHOUShoudong

(Anhui Technical College of Industry and Economy, Hefei 230051, China)

Due to structure defects and limited signal processing technology, MEMS gyro hasthere exists great random error in MEMS gyro. To increase measurement accuracy of MEMS gyro, wavelet threshold denoising method is applied. Firstly, the component of random error in gyro output is analyzed. Then shortcomings of hard threshold and soft threshold function are found through contrast. To solve these shortcomings, improved threshold function is constructed, and through derivation, it can be seen that hard threshold and soft threshold is special case of improved threshold. At last, wavelet threshold denoising scheme is designed and applied in static and dynamic data of MEMS. The result indicates that stability of gyro output increases a degree of magnitude, and the average value is more close to the true value. The proposed the improved wavelet threshold denoising method has good denoising effect.

wavelet threshold denoising; improved threshold function; MEMS gyro; random error

2016-06-20

安徽高校自然科学研究项目(KJ2015A381)

吴 锐(1978-),男,安徽合肥人,讲师,硕士,主要从事计算机网络、物联网方面的研究,(E-mail)ruiwu@qq.com

1673-1549(2016)05-0023-04

10.11863/j.suse.2 016.05.06

TN911.73

A