基于区域统计的遥感地物半自动提取

张 煜，陈文龙，魏思奇，叶 松，曹 波

(长江科学院 空间信息技术应用研究所，武汉 430010)



基于区域统计的遥感地物半自动提取

张 煜，陈文龙，魏思奇，叶 松，曹 波

(长江科学院 空间信息技术应用研究所，武汉 430010)

由于遥感影像的复杂性，面状地物的提取存在着一定的难度。区域统计活动轮廓法有着较强的稳定性和适应性，且在一定的概率密度分布下存在着快速的算法。针对交互式操作的特点，提出了一种基于多边形区域统计活动轮廓的面状地物半自动提取方法，并使用最小描述长度法简化面状地物的轮廓。实验结果显示了该方法在面状地物提取问题上的有效性和实用性。

统计活动轮廓；面状地物；区域提取；随机搜索；最小描述长度

1 研究背景

图像分割与目标轮廓提取是遥感信息提取的重要任务之一，常常作为其较低层次的前处理部分，有着广泛的应用价值。汤育红[1]在地理国情普查中，基于遥感影像的地表覆盖分类提取，需要针对不同地物类型对地表影像进行分割，获取不同地物和人文要素的分布；黄俊等[2-3]基于遥感的水土保持监测需要通过遥感分类对不同地物覆盖的逐年变化进行分析，实现测区内水土侵蚀类型、等级、流失面积、覆盖变化等信息的提取。然而，尽管存在着众多的分割提取方法，却没有一个通用的方法来解决所有的图像分割任务，只能针对不同的实际任务设计不同的算法。基于交互式的半自动提取通常被认为是一种充分结合人工目视识别方式实现快速可靠的分类提取方法，是实际遥感处理工作中常采用的有效的操作方法。

本文基于区域统计的活动轮廓法[4]，增加了可变面积项，并针对半自动交互式操作的特点，提出了基于多边形统计区域的实现方法，同时使用最小描述长度法描述和简化影像目标的轮廓。实验结果显示了本文方法对遥感影像中面状地物提取和分割有着良好的效果。

2 区域统计活动轮廓及其快速算法

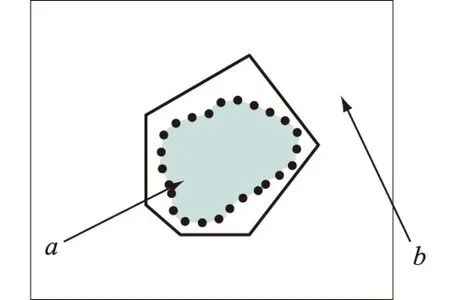
图1 轮廓区域的定义Fig.1Definition of contour

对于给定的影像I={I(x，y)|(x，y)∈[1，Nx]×[1，Ny]}，如图1所示，假设只有一个感兴趣的目标(图中阴影部分)，实线多边形为轮廓的初始位置。轮廓将影像分为轮廓内区域a和轮廓外区域b，在影像灰度为高斯分布条件下，区域统计活动轮廓的能量函数[4]为

(1)

式中：Na和Nb分别为a，b区域的像素数量；σa和σb为a，b区域内像素的标准差。而T被定义如下(以区域a为例)：

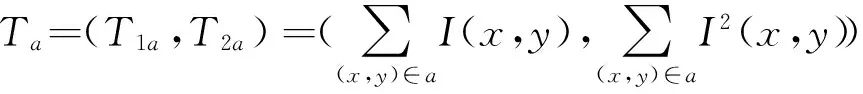
(2)

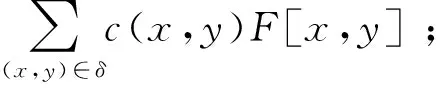
(3)

(4)

式中：针对前述的3个累加量，k分别为0，1，2；图2(a)显示了不同参数的解释，ymax,ymin分别为轮廓在y方向上的最大、最小坐标；而xmax，xmin分别为当前y值下x方向上的最大值和最小值；δ为轮廓；c(x,y)为系数，其值取0，-1，1。

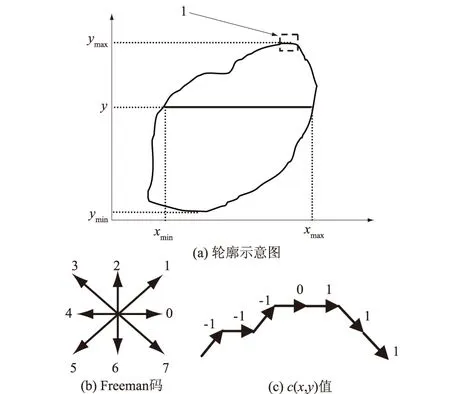
图2 轮廓示意、节点Freeman码和c(x,y)值Fig.2 Illustrations of contour, the direction of Freeman code and the value of c(x,y)

式(4)是实现快速算法的关键，可以在算法迭代前预先处理而求出所有的F[x,y]，而只在迭代过程中通过不同的x,y查找出F[x,y]值即可。于是，对于二维的双重累加被轮廓线上一维累加代替。而系数c(x,y)取1还是-1实际上分别对应着在y取固定值下轮廓线上x方向上最大值和最小值。轮廓线的编码采用如图2(b)所示的Freeman码，通过对于某一点的链入和链出(即上一节点到当前节点和当前节点到下一节点的链码值)，可以建立一个二维表格，针对不同的链入链出值取不同的c(x,y)值，于是跟踪轮廓可以获得所有的c(x,y)值，如图2(a)中1所指示的矩形区域，其链表结构及c(x,y)值如图2(c)所示。于是式(3)可以通过跟踪轮廓快速地求得，并最终能够得到区域a中的3个累加量。因此，实际的二维扫描只在算法迭代前进行了1次，以后的每次迭代计算累加量都是沿轮廓进行的，这样大大提高了计算效率。该算法的具体流程和详细说明可以参见文献[4]。

3 基于多边形区域统计活动轮廓的目标提取

前述方法中区域b为区域a以外的整个影像，然而在实际的影像分割任务，目标地物与背景是很难自动区分的，在多数情况下，目标地物附近可能存在多个其它地物，它们之间的相互位置也不是固定的，因此需要人工目视给出种子点。

本文针对此特点设计了对于任意单连通多边形区域的统计活动轮廓目标提取算法，人工给定的简单初始轮廓将包含完整的感兴趣面状地物以及少量的背景，这样做的好处为：①人为避开干扰物；②减少数据处理量，提高计算速度。其整体的算法流程如图3所示。

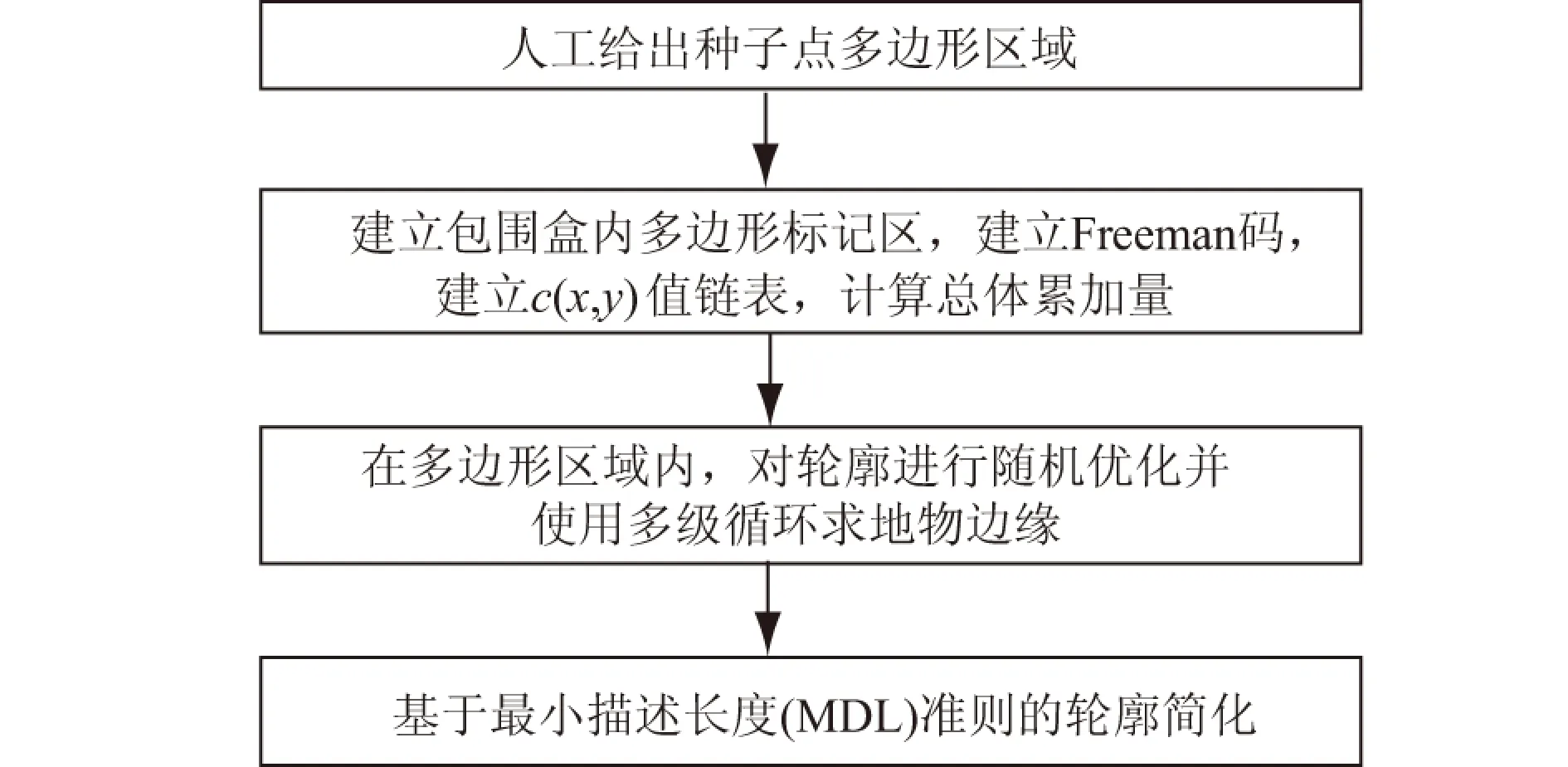
图3 算法流程Fig.3 Flow chart of the algorithm

通过种子点给出背景多边形区域，该区域包含完整的希望提取出的某个地物，因此必须将该多边形标记出来，如图4所示，矩形区域为多边形的包围盒，式(4)的F[x,y]在给出种子点后无需在整个影像区域内计算，而只用在被标记的多边形区域内进行。

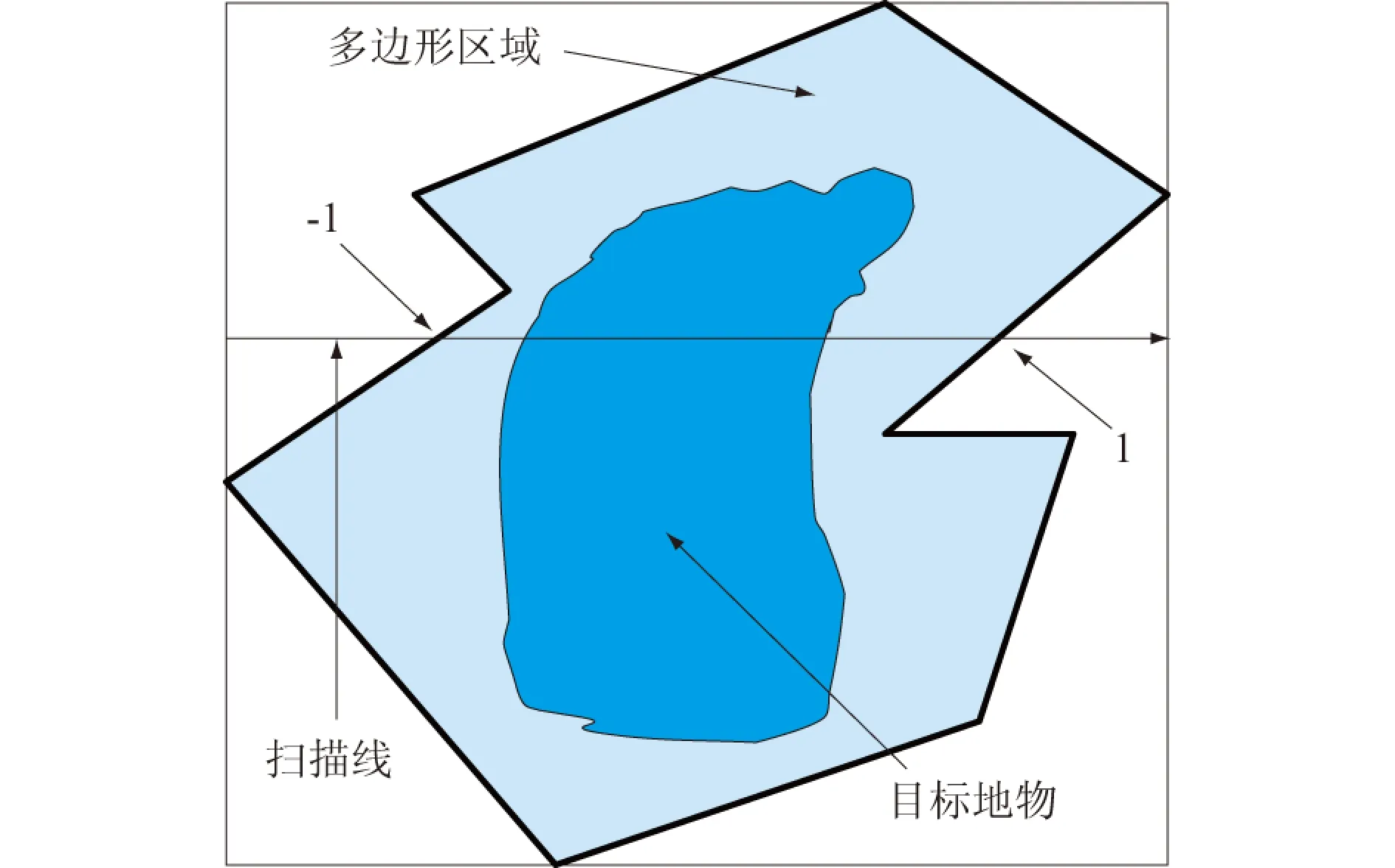
图4 多边形区域示意图Fig.4 Illustration of the polygon

多边形的直线段绘制采用数值微分法，在绘制的同时建立Freeman码，而后基于二维查表法建立c(x,y)值链表，多边形区域的标记直接借用了c(x,y)值链表结构。如图4所示，建立与图中包围盒大小相同的标记区，扫描包围盒标记区，开始时标记区内每点值为0，若扫描线经过c(x,y)链表值-1，则开始将标记区内设置为1，若再扫到c(x,y)链表值为1则停止设置。如此反复，最终建立起多边形区域的标记。

此外，种子点给出的多边形区域不仅要包含目标地物，也要容纳一定数量的背景像素，这就导致了种子点远离了感兴趣的目标地物，尽管活动轮廓演变时利用随机搜索法，但在远离前景的地方仍然容易陷入局部极小值。本文使用了可变面积项使活动轮廓在演变的初始阶段具备较强的向内压力而收缩[5]，而在演化后期该压力逐渐减少，即

(5)

式中：r与随机搜索范围相关，而该范围随后面介绍的多级循环次数的增加而逐渐减小；Na+b为多边形区域内的总像素数量，迭代过程中保持不变；Na为当前轮廓内像素数量。

活动轮廓演化的过程使用了随机最小化方法，具体步骤如下：

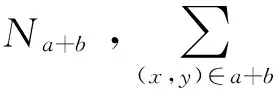
(2) 进行一次某个轮廓点的移动，等概率随机选择某个轮廓点，将该点由开始位置(x,y)移动到(x+dx，y+dy)，其中dx，dy的变化范围为(-r，r)，而dx或dy的取值也是等概率的在范围(-r，r)中选取。

(3) 进行移动点的交叉测试和有效区域测试，交叉测试确保轮廓在演化过程中不会出现自相交，而有效区测试通过使用多边形标记区确保轮廓节点的移动不会超出多边形区域的边界。如果测试不通过则放弃当前的移动。

(4) 依式(5)，如果当前计算出的E′小于以前的则移动有效，否则放弃移动。

将以上步骤(2)—步骤(4)迭代指定次数后为一次循环。由于人工给定的初始点通常较少，直接使用这些控制点作为轮廓点无法满足复杂地物的边缘拟合，算法采用多尺度方法，具体的实现过程是：第1次循环的多边形为人工给定的少量种子点，此时由于种子点离前景较远，可以使用较大的r值范围，即较大的随机搜索步伐，于是一个近似的较少点的边缘轮廓产生且尽可能地与目标地物吻合;第2次循环，活动轮廓的节点将根据特定的阈值th而增加，凡是多边形的某线段的距离大于th的就在该线段中间增加一个节点，如此反复地增加直到所有的边长度都小于该阈值th，然后再运行随机搜索算法，而活动轮廓随机搜索循环中使用的搜索范围r也依循环次数相应地减小。后续的循环过程与第2次循环类似，th与r都相应减小。一般而言，经过3—4次循环，活动轮廓可以收敛到较好的结果。

图5显示的是4次循环迭代结果，其中，图5(a)为人工给定初始多边形轮廓，共6个种子点，经过300次随机动态演化的循环，6点形成的多边形紧靠目标地物的边缘。注意图5(b)中轮廓顶端出现的尖点，由于考虑活动轮廓随机演变效率而未采用平滑项，尖点出现是难免的，因此每次迭代完成后都需要检测和删除这些尖点，也可以使用最小描述长度法在简化轮廓的时候自动去除。

图5 多尺度方法不同循环阶段结果Fig.5 Results of different stages of multiple scale method

4 基于最小描述长度准则的轮廓简化

为了达到与目标地物边缘一致，活动轮廓的节点数量越多越好，但是节点数量过多对于轮廓的存储和描述都不利。本文采用了最小描述长度法来简化轮廓。最小描述长度法是由J.Rissanen[6]提出，用来描述数据的平均复杂度，该准则认为，评估一组数据复杂度的最好方法是同时考虑对数据模型的编码码长以及模型参数本身的编码码长。本文中，数据模型编码包括对区域a和b的编码，而参数编码即是对活动轮廓节点位置的编码，其总的码长可以表达为

(6)

式中：Pa与Pb分别为a，b区域像素灰度值分布；k为活动轮廓节点数量；L()为总码长，在影像灰度为高斯分布条件下，由式(1)的推导过程，基于最小描述长度准则的能量函数可以写为

Nblgσb+klgNa+b=E+klgNa+b。

(7)

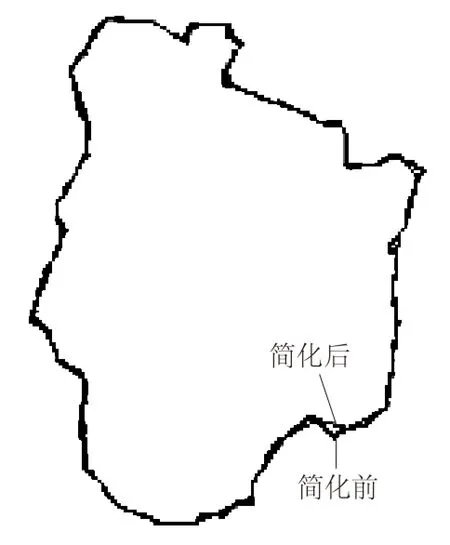
图6 简化前后轮廓叠加显示Fig.6 MDL contour superimposed on contour without MDL

可见，使用基于最小描述长度准则只需在原来的能量函数基础上增加一项活动轮廓的编码长度即可。实际应用时，该准则并不适合于一开始就使用，这样会导致在节点数量不多时无法准确匹配边缘，有效可行的方案是先使用式(5)过度增加节点，然后基于式(7)逐个删除多余节点，即每次删除能使EMDL下降最快的轮廓点。图6显示了采用EMDL对轮廓进行简化后与使用E’的简化前的轮廓叠加，可见二者的差别非常小，但是简化前轮廓节点数为173，简化后为51。

5 实验与验证

本文实验数据为航空影像，在假设影像灰度为高斯分布的基础上，使用式(5)和式(7)并基于文中的方法对图像中的面状地物进行提取。图7显示的是人工给定的初始多边形(即提取前的图像)和对应的提取结果。对于相对孤立的面状地物如图7(a)和图7(b)，提取可直接使用矩形作为初始多边形，而图7(c)和图7(d)的图像前后景关系复杂，更适合采用多边形以获得正确的结果。图中的面状地物普遍没有明显的边缘，前后景的差别也不是特别清晰，直接使用基于边缘或基于简单的均匀区域分割的方法都很难将感兴趣的区域提取出来。

图7 影像提取前后的实验结果Fig.7 Experiment results before and after image extraction

6 结 论

本文所用的多边形区域统计活动轮廓对这类物体的提取有着很好的适应性，算法的抗干扰能力较强，对种子点的位置也没有严格的要求，算法的收敛经过了4次循环，分别经过了300，400，500，600次迭代，节点随机移动范围以像素为单位分别是20，10，4，2，分级阈值th除了第1次由于人工给定而无th外，其它3次分别是30，10，5。实验结果显示了本文方法的有效性和实用性。

[1] 汤育红. 地理国情普查地表覆盖与国情要素信息的提取方法探讨[J]. 测绘与空间地理信息，2013，36(12):89-91.

[2] 黄 俊，申邵洪. 结合高分辨遥感影像和GIS数据的土地利用变化监测[J]. 长江科学院院报，2012，29(1):49-52.

[3] 孟广涛, 方向京, 和丽萍，等. 3S技术在水土保持动态监测中的应用[J]. 水土保持研究，2007，14(2)：8-10.

[4] CHESNAUD C, REFREGIER P, BOULET V. Statistical Region Snake-based Segmentation Adapted to Different Physical Noise Models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1999，21(11)：1145-1157.

[5] RONFARD R. Region-based Strategies for Active Contour Models[J]. International Journal of Computer Vision, 1994, 13(2):229-251.

[6]RISSANEN J.Hypothesis Selection and Testing by the MDL Principle[J]. Computer Journal, 1999, 42(4)：260-269.

(编辑：黄 玲)

Target Extraction Based on Polygon StatisticalRegion-based Active Contour

ZHANG Yu，CHEN Wen-long，WEI Si-qi，YE Song，CAO Bo

(Spatial Information Technology Application Department, Yangtze River Scientific Research Institute, Wuhan 430010, China)

Active contour is an important method to segment images. Its segmentation strategy is usually edge-based or region-based and based on the contour energy minimization. But the classical active contour is difficult to deal with the region which has weak edges or is in the complicated background. In this paper, we implement an improved statistical region-based active contour and propose a strategy to extract region of interest by polygon. Within the family of exponential probability density function, statistical region-based active contour can run by fast algorithm. We give details of the realization of the algorithm and simplify the contour by the minimum description length. Experiment results illustrate the efficiency of our proposed method in contour extraction.

statistical active contour; planar features; region extraction; random search; minimum description length

2016-08-20

云南省水利重大科技项目(CKSK2015852/KJ)；云南省省级水资源费项目(CKSK2015720/KJ)

张 煜(1971-)，男，山东阳谷人，高级工程师，博士，研究方向为摄影测量与遥感，(电话)18986061273(电子信箱)zhangyu_1999@126.com。

10.11988/ckyyb.20160855

2016,33(11):12-16

P237

A

1001-5485(2016)11-0012-05