双阈值Alpha Shapes算法提取点云建筑物轮廓研究

李云帆，谭德宝，高 广，刘 瑞

(1.长江科学院 空间信息技术应用研究所，武汉 430010; 2.深圳飞马机器人科技有限公司，广东 深圳 518000；3.哈尔滨工业大学 深圳研究生院，广东 深圳 518055;4.深圳市房地产评估发展中心，广东 深圳 518040)



双阈值Alpha Shapes算法提取点云建筑物轮廓研究

李云帆1，谭德宝1，高 广2，刘 瑞3,4

(1.长江科学院 空间信息技术应用研究所，武汉 430010; 2.深圳飞马机器人科技有限公司，广东 深圳 518000；3.哈尔滨工业大学 深圳研究生院，广东 深圳 518055;4.深圳市房地产评估发展中心，广东 深圳 518040)

针对单一阈值的Alpha Shapes算法在提取点云建筑物轮廓时存在的轮廓精度和完整性难以兼顾的问题，提出一种双阈值的Alpha Shapes算法，利用简单环的概念设计轮廓搜索算法，获得既有较好完整性又有较高几何精度的建筑物轮廓线；然后，利用一种最小二乘的轮廓线化简算法对提取出的初始轮廓进行化简，与经典的Douglas Peucker算法相比，在存在噪声的情况下，该方法化简后的轮廓线更接近实际的轮廓线。

LiDAR；建筑物轮廓提取；RANSAC；Alpha Shapes算法

1 研究背景

建筑物的轮廓信息是建筑物提取与三维模型重建的重要基础，已广泛应用于城市基础信息库更新、目标识别、灾害预估、变化检测、房地产等领域[1]。目前，基于机载LiDAR数据追踪建筑物平面轮廓的一般方法是将点云内插成深度影像，然后利用图像分割算法对深度影像进行分割，最后用扫描线法、邻域搜索法等方法实现建筑物边界的追踪[2-5]。这些方法存在的问题是所追踪到的边缘是离散点集的粗略边界，精度较低。也有一些学者研究了直接从离散点集提取其轮廓的方法，如黄先锋等[6]提出一种基于平面离散点的边缘追踪算法，该算法将边长比作为约束条件，降低了算法参数对点密度的依赖性，从而提高算法对细长特征或分布不均匀的点集边缘提取的适应性，但是约束条件的阈值设置不当易造成边缘过渡收缩的现象；Alpha Shapes算法最早由Edelsbrunner等[7]提出，后来许多学者对其进行改进并应用于机载LiDAR数据处理领域，该算法理论完善、效率高，还能够处理较复杂的建筑物轮廓提取问题，主要缺点是不适用于分布不均匀的数据，同时算法参数的选择也较困难。

从点云中提取建筑轮廓可归结为恢复离散点集的原始形状，而Alpha Shapes算法[7]是一种有效的方法。Alpha Shapes算法是一种确定性算法，有着严格的数学定义，对于任意一个有限点集S，Alpha Shapes算法得到点集形状∂S是确定的，另外，用户还可以通过调整算法的唯一参数α来控制点集形状∂S的精细程度。鉴于Alpha Shapes算法的优良性能，国内外不少学者提出利用Alpha Shapes算法直接从机载LiDAR数据提取建筑物轮廓线[8-10]。但是，在实际应用中，仍存在一些问题需要解决：①Alpha Shapes算法主要适用于密度相对均匀的点集数据，这是由算法的本质决定的，因为点集形状的精细程度完全由参数α控制，单一参数的Alpha Shapes算法无法适应密度差异较大的点集数据；②Alpha Shapes算法在处理凹型点集时处理效果不太好，如果α值较大的话，凹拐角容易被钝化掉，如果α值较小的话，又容易得到破碎的点集形状，沈蔚等[9]指出，应该将α值设置为1～2倍的平均点间距，此时得到的点集形状相对完整又不会太破碎。

针对上述问题，本文提出一种双阈值的Alpha Shapes算法，用来完整地提取建筑轮廓;然后，采用基于最小二乘的轮廓线对提取出来的初始轮廓线进行化简。

2 基于双阈值Alpha Shapes算法的轮廓线提取

2.1 双阈值α-shape的获取

令DT(S)为点集S的Delaunay三角网，∂S1，∂S2分别为参数设置为α1和α2时Alpha Shapes算法得到的α-shape，文献[7]已证明任意阈值下的α-shape均为DT(S)的子集，即∂S1⊂DT(S)，∂S2⊂DT(S)，因此α-shape的获取过程为：首先采用逐点插入算法构建点集S的Delaunay三角网DT(S)(详见文献[11])，然后依次对DT(S)中的每条边进行Alpha Shapes测试，如图1所示，pq为DT(S)中的一条边，圆C为过pq且半径为α的圆(圆心坐标见式(1)和式(2))，如果没有其他顶点在圆C内，则边pq属于α-shape。

(1)

(2)

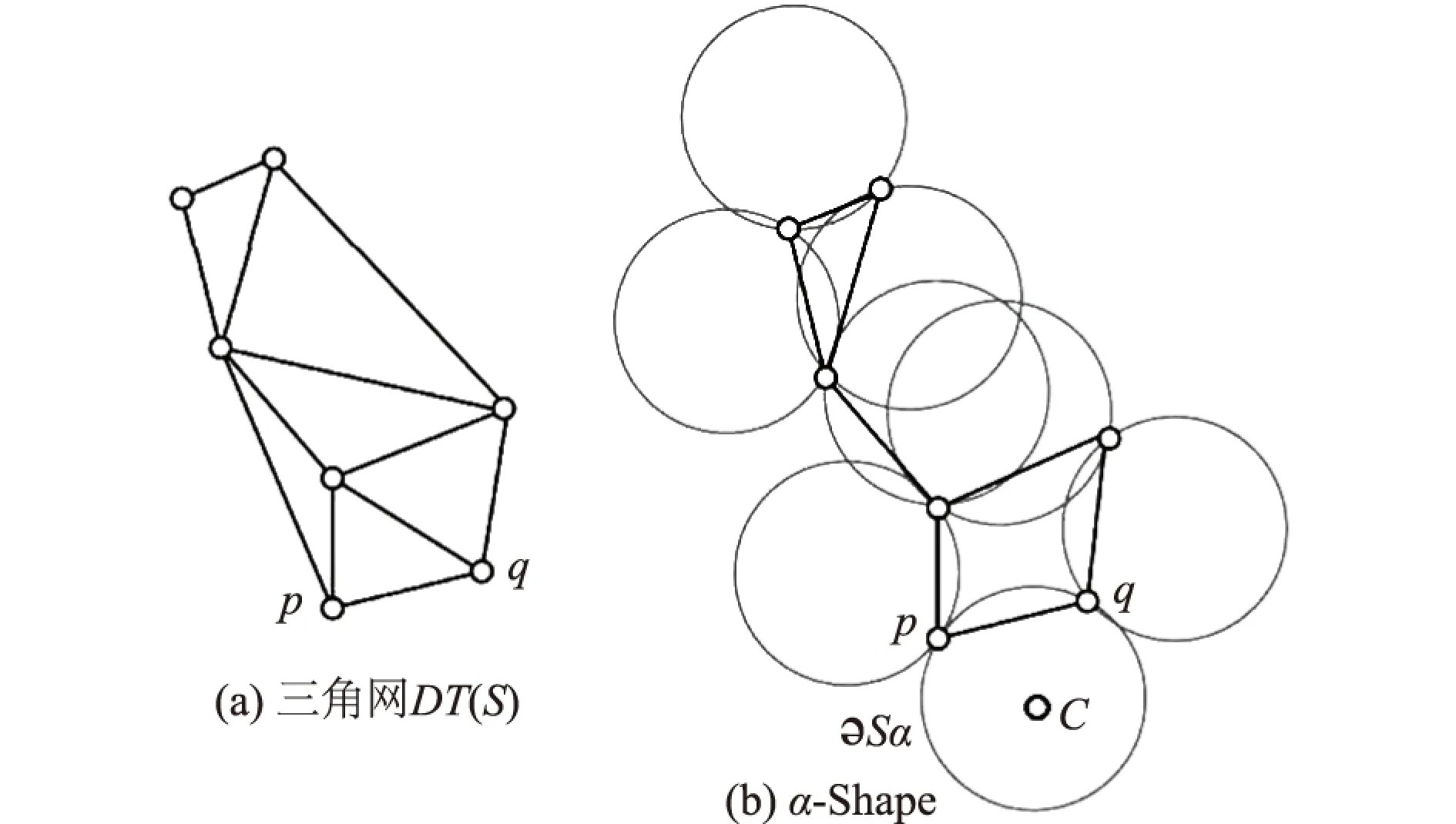
图1 Alpha Shapes测试原理Fig.1 Principle of Alpha Shapes test

2.2 基于广度优先搜索的简单环查询算法

基于广度优先的搜索算法可以用来进行无向图顶点遍历，本文提出一种搜索策略，可以显著提高搜索效率。

首先引入2个关键概念：简单路径和简单环。简单路径指一个无向图内，从某个起点出发，经过不重复的端点到达另外一个端点的过程中所形成的路径；简单环指一个无向图内，从某个起点出发，经过一条简单路径回到起点所形成的路径。

令G为∂S1和∂S2中的边所构建的无向图，建立无向图G的邻接表L，假设p为无向图G中的任一顶点，from[p]表示从某一起点出发，在到达终点p之前所经过的最后一个顶点；dist[p]表示从某一起点出发到达终点p所经过的简单路径的长度。利用dist[p]可以仅搜索一定长度阈值内(如20 m)的简单环，从而显著提高算法的搜索效率。以下为算法具体步骤。

步骤(1)：按顺序从无向图G中选取一个顶点p，令p为起点，经过p的简单环为Loop，将所有from值设置为null，将起点p的dist值设置为0，其他顶点的dist值设置为无穷大，根据邻接表L创建无向图G的邻接矩阵M，将p压入搜索队列Q中。

步骤(2)：从搜索队列Q中取出最早压入的顶点q，转步骤(3)。

步骤(3)：根据邻接表L依次判断q的邻接点qi。①查询邻接矩阵M，如果q与qi不相连，则判断一下邻接点；②在邻接矩阵M中，将q与qi邻接关系去除，避免该路径被多次经过；③判断邻接点qi是否已经加入过队列，如果qi没有加入过队列(即dist[qi]为无穷大)，转④，否则转⑤；④更新from[qi]为q，dist[qi]为dist[q]+d(q,qi)，如果dist[qi]<阈值条件，则将qi加入到搜索队列Q中，返回步骤(3)继续判断下一个邻接点；⑤判断路径p-q-qi-p是否为简单环，如果是简单环且该环的长度比Loop短，则将Loop更新为该环。

步骤(4)：如果搜索队列Q不为空，记录Loop并转步骤(2)，否则转步骤(1)。

2.3 对应路径筛选

筛选过程仅考虑由简单路径l1和l2构成的简单环，其中l1和l2分别属于∂S1和∂S2。筛选过程分以下3种情况进行讨论：

(1) 如图2(a)所示，如果l1的长度是l2的5倍以上，则丢弃l1，保留l2。

(2) 如图2(b)所示，如果l2的两个邻边接近垂直，且l1上所有端点到l2任一邻边的距离均较小，则丢弃l2，保留l1。

(3) 如图2(c)所示，如果l2与l2两个邻边接近平行，且l1上的端点到l2的距离小于一定的阈值(如0.5倍的平均点间距)，则丢弃l1，保留l2。

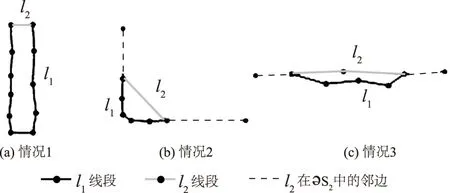
图2 对应路径筛选的3种情况

2.4 闭合轮廓线获取

由第2.1—2.3节步骤获得的中间结果是一些离散的边，而最终所需的建筑物轮廓线是按顺序连接的闭合多边形。该过程可以采用基于深度优先的搜索算法，算法详细流程与步骤(2)类似，主要有2点不同：基于深度优先的搜索算法使用堆栈，而基于广度优先的搜索算法使用队列；基于深度优先的搜索算法的目标是长度大于阈值的环，而基于广度优先的搜索算法的目标是长度小于阈值的环。

图3 提取的某栋建筑物轮廓Fig.3 Results of extracting building contour

3 基于最小二乘的轮廓线化简

利用双阈值的Alpha Shapes算法得到的建筑物闭合轮廓非常粗糙，一般需要先对其进行化简处理。Douglas Peucker算法是一种经典的矢量压缩算法，被众多GIS系统所采用。针对建筑物轮廓线化简问题，Douglas Peucker算法存在易受噪声点干扰的问题。

本文提出一种基于最小二乘法的轮廓线化简算法，该算法需要2个参数，即距离阈值dmax和长度阈值L，算法的详细步骤如下所示。

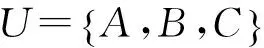
(2) 令集合U的两端点为P和Q，分别以P和Q为起点向两侧增长，增长过程中将会遇到新的顶点，如果新的顶点到直线L的距离

(3) 如果步骤(2)中有新的顶点加入到集合U中，则对集合U进行最小二乘拟合，得到新的直线L，转步骤(2)；否则转步骤(4)。

(4) 判断集合U的长度，如果U的长度大于阈值L，则保留集合的两端点，丢弃中间顶点。

(5) 如果还有连续的3个顶点集都没有判断过，转步骤(1)；否则判断长度阈值L的大小，如果L大于2～3倍的平均点间距，缩小长度阈值至0.8L，转步骤(1)。

4 实验结果

选取一栋建筑物点云为实验数据(如图3(a))，该数据已经过了分类处理，一共包含9 170个建筑物激光脚点，平均点间距约为0.75m。双阈值AlphaShapes算法采用的α值为0.5m和1.5m。图3(b)为α值为0.5m时AlphaShapes算法得到的建筑物轮廓，由于机载LiDAR数据不太均匀，在有些地方处点间距>1m(2倍的α值)，如图3(b)的上方较多虚假的轮廓线被提取出来，但是在凹拐角处的建筑物轮廓线比较精确地描述了建筑物的原始形态；图3(c)为α值为1.5m时AlphaShapes算法得到的建筑物轮廓线，该轮廓线整体比较完整，但是存在比较明显的凹拐角被钝化的问题，在图中用圆形标注出了一个凹拐角被钝化的示例；图3(d)是对图3(b)和图3(c)的提取结果构建无向图后，利用广度优先搜索算法得到的简单环，可以发现存在问题的虚假轮廓和凹拐角基本都被包含在提取出的简单环中，通过对简单环的筛选，得到如图3(e)所示的建筑物轮廓，该轮廓既有较好的完整性，又能够较精确地描述建筑物的原始形态；最后对图3(e)中提取的轮廓线施用基于最小二乘法的化简算法，得到化简后的建筑物轮廓线。

5 结 语

从建筑物点云中提取轮廓线是车载、机载激光雷达数据处理中的一个热门研究方向。本文提出一种新的建筑物轮廓线提取和化简方法，该方法主要有2个优点：

(1) 针对单一阈值的AlphaShapes算法存在轮廓精度和完整性难以兼顾的问题，提出一种双阈值的AlphaShapes算法，利用简单环的概念设计轮廓搜索算法，可以获得既有较好完整性又有较高几何精度的建筑物轮廓线。

(2) 采用一种基于最小二乘的轮廓线化简算法，与经典的DouglasPeucker算法相比，在存在噪声的情况下，该算法化简后的轮廓线更接近实际的轮廓线。

采用真实的机载点云数据设计实验，证明了本文方法的有效性。但是该方法仍然存在不足之处，譬如AlphaShapes算法的双阈值的取值自适应性不高，对点云数据本身特征利用不足，这也是下一步的研究方向。

[1]SAMPATHA,SHANJ.BuildingBoundaryTracingandRegularizationfromAirborneLiDarPointClouds[J].PhotogrammetricEngineeringandRemoteSensing, 2007, 73(7): 805.

[2]钱 韬. 从DSM数据中自动提取建筑物的方法研究[J]. 测绘与空间地理信息, 2008, 31(6): 137-140.

[3] 杨 洋，张永生，马一薇，等. 基于LiDAR数据的建筑物轮廓提取[J]. 测绘科学, 2010, 35(3): 203-205.

[4] 王大莹，程新文，潘慧波，等. 基于最佳阈值形态学方法对机载LiDAR数据进行边缘提取[J]. 测绘工程, 2009, 18(2): 34-37.

[5] 马 文，岳建平，曹 爽. 基于影像分割技术的LiDAR数据建筑物边缘提取[J]. 地理与地理信息科学, 2010, 26(4): 57-59.

[6] 黄先锋，程晓光，张 帆，等. 基于边长比约束的离散点准确边界追踪算法[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 688-691.

[7]EDELSBRUNNERH,KIRKPATRICKD,SEIDELR.OntheShapeofaSetofPointsinthePlane[J].IEEETransactionsonInformationTheory, 1983, 29(4): 551-559.

[8] 李云帆. 机载LiDAR数据联合航空影像的城市建筑物三维重建研究[D]. 武汉：武汉大学, 2012.

[9] 沈 蔚，李 京，陈云浩，等. 基于LiDAR数据的建筑轮廓线提取及规则化算法研究[J]. 遥感学报, 2008, 12(5): 692-698.

[10]JOCHEMA,HÖFLEB,RUTZINGERM, et al.AutomaticRoofPlaneDetectionandAnalysisinAirborneLiDarPointCloudsforSolarPotentialAssessment[J].Sensors, 2009, 9(7): 5241-5262.

[11]DEBERGM,VANKREVELDM,OVERMARSM, et al.ComputationalGeometry[M].US:Springer, 2000.

(编辑：王 慰)

Extraction of Building Contour from Point Clouds Using DualThreshold Alpha Shapes Algorithm

LI Yun-fan1，TAN De-bao1，GAO Guang2，LIU Rui3,4

(1.Spatial Information Technology Application Department, Yangtze River Scientific Research Institute,Wuhan 430010, China; 2.Shenzhen Feima Robotics Co., Ltd., Shenzhen 518000, China;3.Shenzhen Graduate School, Harbin Institute of Technology，Shenzhen 518055, China；4.Center for Assessment and Development of Real Estate Shenzhen, Shenzhen 518040, China)

To balance the contour accuracy and completeness of single threshold Alpha Shapes in extracting point cloud building contours, we present a dual-threshold Alpha Shapes algorithm using a simple ring design concept contour search algorithm to obtain both a good integrity and a relatively high geometric precision of the building’s contour. Furthermore, the initial contour is simplified based on least squares algorithm. In the presence of noise, the simplified contour lines of the present algorithm are closer to the actual contours compared with the classic Douglas Peucker algorithm.

LiDAR; building boundaries extraction; RANSAC; Alpha Shapes algorithm

2016-08-10

中央级公益性科研院所基本科研业务费项目(CKSF2014031/KJ)；云南省水利重大科技项目(CKSK2015852/KJ)

李云帆(1984-)，男，湖北恩施人，工程师，博士，主要从事机载、车载激光雷达点云数据处理方向研究，(电话)13429843035(电子信箱)yun_di@sina.com。

10.11988/ckyyb.20160811

2016,33(11):1-4

P237

A

1001-5485(2016)11-0001-04