基于量子遗传算法的永磁同步电动机混沌运动的同步控制*

何　颖，张海丽*，鹿　剑，竟静静

（1.新疆工程学院电力工程系，乌鲁木齐830091；2.新疆维吾尔自治区特种设备检验研究院，乌鲁木齐830011）

基于量子遗传算法的永磁同步电动机混沌运动的同步控制*

何颖1，张海丽1*，鹿剑2，竟静静1

（1.新疆工程学院电力工程系，乌鲁木齐830091；2.新疆维吾尔自治区特种设备检验研究院，乌鲁木齐830011）

混沌同步是当代非线性与控制学科中的一个热点问题。针对永磁同步电动机中混沌同步，反馈反同步法在整定反馈增益矩阵参数时存在困难，利用量子遗传算法对反馈增益矩阵进行参数优化，从而克服反馈增益中参数不易整定的缺陷。数值仿真实验表明，利用量子遗传算法结合反馈反同步法能够使初始状态不同、运动轨迹不同的两个混沌系统在短时间内迅速达到同步，可以是系统达到很好的动态特性，验证了该方法的有效性，对电动机运动的稳定性具有较好的价值。

永磁同步电动机；混沌同步；量子遗传算法；反馈反同步

永磁同步电动机混沌控制是非线性科学中的一个热门研究领域。自从美国物理学家Ott等人提出开拓性的工作，混沌同步已被广泛研究，提出了许多行之有效的方法，常用的控制方法有强迫迁徙法［1］、自适应控制、延时反馈控制［2-3］等。

永磁同步电动机是一种典型的多变量、强耦合非线性系统，在某些参数及工作条件下会呈现混沌行为［4］，当电机运动在混沌状态下时，系统状态出现不规则运动，直接影响了电机运行的质量和稳定性，如何对永磁同步电动机系统中的混沌行为进行控制已成为关注的焦点。首先对永磁同步电动机的数学模型进行了精确线性化，然后利用相应的技术将其控制到平衡点，然而此方法较为复杂，使得物理实现较为困难［5］。

量子遗传算法［6］QGA（Quantum Genetic Algorithm）是近几年新发展起来的一种量子计算和遗传算法相结合的一种优化方法。QGA是以量子计算的一些概念和理论为基础，用量子位编码来表示染色体，量子旋转门作用更新来完成进化搜索，量子进化计算的结果可以增加遗传算法的种群多样性，避免早熟现象。本文基于永磁同步电机中混沌运动的同步状态反馈控制，利用量子遗传算法对反馈增益矩阵进行参数优化，实现了永磁同步电动机中的混沌同步控制。

1　永磁同步电动机的数学模型及其混沌特性分析

在d-q轴坐标系下考虑均匀气隙的永磁同步电动机（Ld=Lq）的无量纲模型。id，iq，w为系统状态变量，分别表示d轴定子电流、q轴定子电流和转子机械角速度w，永磁同步电动机的数学模型可以写为［6-7］

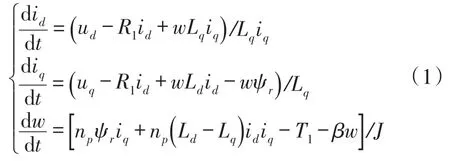
上述模型经过仿射和时间尺度变换后的均匀气隙永磁同步电动机数学模型为

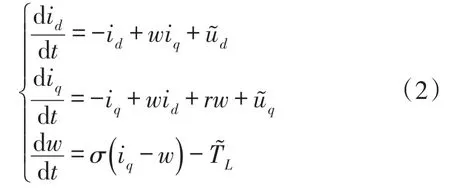
一般情况下，考虑电动机系统没有外力的情形。可以看做永磁同步电动机空载运行一段时间后突然断电，各外部输入项均为零的情形，也就是=0，=0和=0。此时，式（2）系统可表述为

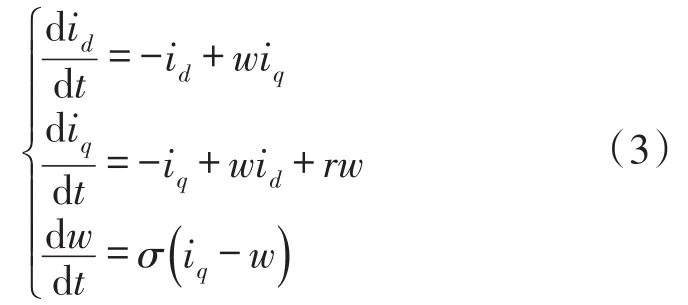
σ=5.46，γ分别为16、20、100时，式（3）系统存在不同参数下呈现不同的动态行为。此时永磁同步电动机表现为混沌行为，不同参数下各状态变量的运动轨迹如图1所示。混沌的存在将严重破坏永磁同步电动机的稳定运行，甚至会引起传动系统的崩溃，。所以必须抑制永磁同步电动机的混沌运动。

图1　永磁同步电动机的d-q定子电流相序图

2　量子遗传算法对永磁同步电动机混沌运动的同步控制

2.1量子遗传算法

量子遗传算法（QGA）是将量子计算（Quantum Computing）和遗传算法（GA）相融合，在近几年研究较为火热的一种全新智能算法。QGA中单个染色体能够表示多个态的叠加，所以QGA比传统GA更容易保持种群的多样性，具有对目标问题更优化的求解［7，8］，理论上已经证明［9］。

QGA与GA本质上的区别是染色体用量子比特来表示，编码的过程是用量子坍缩的形式，群体中个体的更新是用量子旋转策略来实现，QGA具体操作如表1所示。

表1　量子遗传算法具体操作步骤

2.2对永磁同步电动机混沌运动的同步控制

混沌系统的状态方程如式（4）所示

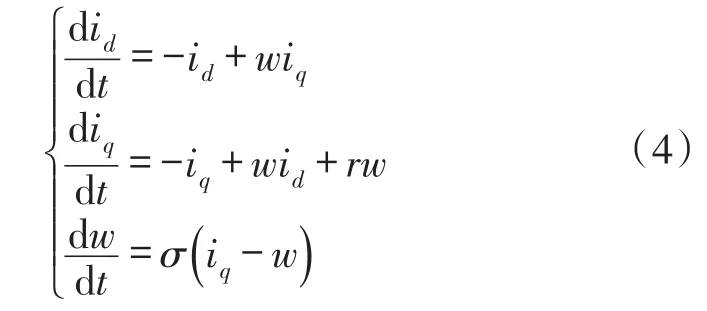
式中，σ=5.46，r分别为16、20，电机处在混沌状态x，y两种状态，导致永磁同步电机的不稳定。现将状态误差的反馈引入同结构的混沌系统当做响应系统，e为状态误差，x，y分别是驱动状态和随动状态，k=diag（k1，k2，k3）为反馈增益矩阵。

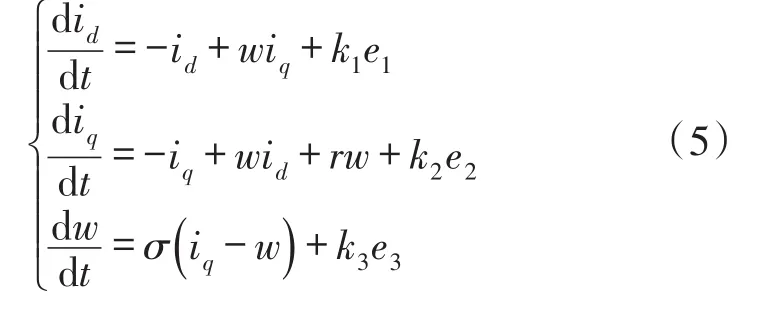
根据混沌同步的定义，若状态向量误差满足下列条件：

则称永磁同步电动机运动完全同步的。其中，x0和y0分别是x和y的初始值。但是在实际系统中，达到同步所需要的时间不可能无限长，最好是时间用的越少越好。

图2　基于QGA的混沌同步方法原理示意图

3　仿真实验与结果分析

由于混沌系统中，对初值的选取极其敏感，所以任何一个系统中，状态变量所选取的初值不同，则运动轨迹不同。

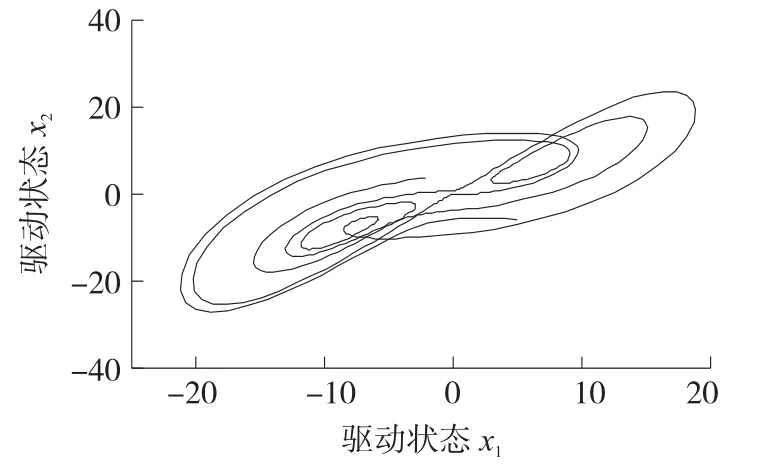
图3　驱动系统x1和x2的运动轨迹

图4　随动系统y1和y2的运动轨迹

QGA中参数设置为：种群大小为20，遗传代数为50，二进制长度为20。通过测量解码得到反馈增益k阵中k1，k2，k3，调用在Simulink中构建出的驱动系统与随动系统结构，以式（6）作为参数引导，反馈增益k阵所优化结果为k=diag（889，912，863），则随动系统与驱动系统达到同步状态。状态x1，x2和状态y1，y2同步的情形如图5所示。

图5　状态x1、x2和状态y1、y2同步的情形

如图5所示，随动系统的状态y1，y2在很短的时间内就和驱动系统的状态x1，x2重合。图6～图8分别表示的是状态x1、y1和x2、y2以及x3、y3随时间同步的情形。

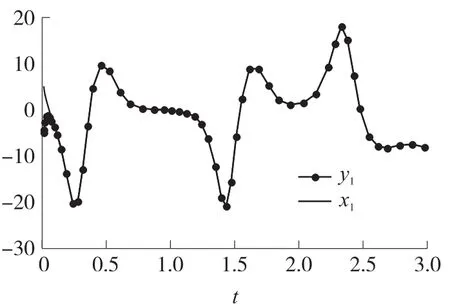
图6　状态x1和y1随时间同步情形

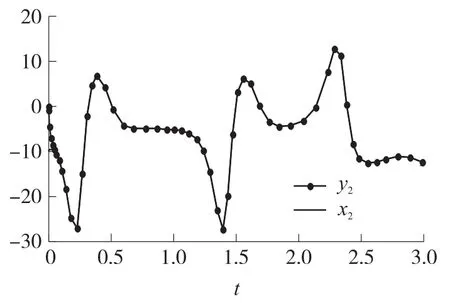
图7　状态x2和y2随时间同步情形

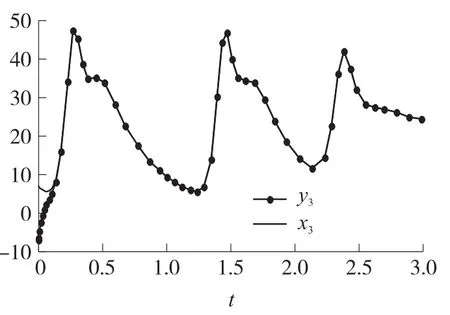
图8　状态x3和y3随时间同步情形

由上几幅图可以看出，在很短的时间内就可以达到同步状态，运动轨迹完全重合，误差的变化曲线如图9所示。

图9　误差e1、e2和e3随时间变化情形

针对混沌的同步问题，将其误差反馈进入量子遗传算法的调整中，实验结果显示，利用量子遗传算法所调解的参数增益，可以将永磁同步电动机两个初始状态不一样的混沌系统到达相同的轨迹，所得的误差也在很短的时间内归位于零，说明了量子遗传算法在系统的同步问题上起到了良好的作用。

4　结论

本文针对永磁同步电动机初始取值不同的混沌运动进行同步研究，实现了永磁同步电动机中的混沌控制。永磁同步电动机运动轨迹完全不同的两个混沌系统通过量子遗传算法，与反馈同步法相结合，对反馈增益矩阵进行参数优化，将初始状态不同、运动轨迹不同的两个混沌系统在短时间内迅速达到反同步，说明了本文所采用量子遗传算法在解决永磁电动机混沌系统同步问题上开拓了一种新方法，具有较高的应用价值。

［1］Meng Fanwei，Liu Chengying，Li Zhijun，et al.Adaptive PI Control Strategy for Flat Permanent Magnet Linear Synchronous Motor Vibration Suppression［J］.Chinese Journal of Mechanical Engineering，2013（1）：11-20.

［2］李俊，陈基和，邹国棠.永磁直流电机的混沌反馈控制［J］.中国电机工程学报，2006，26（8）：77-81.

［3］张兴华，王德明.无刷直流电机混沌系统状态反馈控制仿真研究［J］.微电机，2009，42（11），82-85.

［4］王华，邹积浩.基于模糊逻辑的直线永磁同步电机直接推力控制［J］.电子器件，2007，3（6）：2280-2283.

［5］韦笃取.罗晓曙.基于LaSalle不变集定理自适应控制永磁同步电动机的混沌运动［J］.物理学报，2009，58（9）：6026-6029.

［6］Han K H，Kim J H.Genetic Quantum Algorithm and Its Application to Combinatorial Optimization Problem［C］//Evolutionary Computation，2000.Proceedings of the 2000 Congress on.IEEE，2000，2：1354-1360.

［7］Zhang B，Li Z，MAO Z，et a1.Study on Chaos and Stability in Permanent-Magnet Synchronous Motors［J］.Journal of South China University of Technology，2000，28（12）：120-125.

［8］张波，李忠，毛宗源.永磁同步电机的混沌模型及其模糊建模［J］.控制理论与应用，2002，19（6）：841-844

［9］Kong Haipeng，Li Ni，Shen Yuzhong.Adaptive Double Chain Quantum Genetic Algorithm for Constrained Optimization Problems［J］.Chinese Journal of Aeronautics，2015（1）：214-228.

何颖（1965-），女，新疆人，硕士，教授，从事电气工程，控制理论与控制工程，量子物理学，425287215@qq.com；

张海丽（1989-），女，汉族，新疆，新疆工程学院电力工程系，讲师，主要研究方向为电气工程，控制理论与控制工程，智能控制，量子物理学，425287215@qq.com。

Chaos Synchronization Control for Permanent Magnet Synchronous Motor Based on Quantum Genetic Algorithm*

HE Ying1，ZHANG Haili1*，LU Jian2，JING Jingjing1
（1.Xinjiang Institute of Engineering，Department of Electric Power Engineering，Urumqi 830023，China；2.Special Inspection Institute of Xinjiang Uygur Autonomous Region，Urumqi 830011，China）

The nonlinear chaoctic synchronization is a hot issue in the contemporary nonlinear control subject.For the permanent magnet synchronous motor has difficulty of chaos synchromzation in tuning in the feed back gain matrix parameter of feed back anti synchronization method，quantum genetic algorithm can be used to optimize the parameters of feed back gain matrix and to overcome tuning defects of the feed back gain parameters.Numerical simulations show that quantum genelic algorithm combined with feed back anti synchronization method enables two different chaotic systems with the different initial states and different trajectories to achieve synchromatization in a short time.The system can achieve excellent dynamic charactiristic and verify the method effectiveness.It has good value in stability of the motor motion.

PMSM；chaotic synchronization；quantum genetic algorithm；feedback anti-synchronization

TP18

A

1005-9490（2016）05-1251-04

项目来源：新疆工程学院科研基金项目（2014xgy191612）

2015-10-31修改日期：2015-12-18

EEACC:8310D10.3969/j.issn.1005-9490.2016.05.044