某减震器压杆稳定性探究

康水库，刘 勇

（陕西通力专用汽车有限责任公司，陕西 宝鸡 722045）

某减震器压杆稳定性探究

康水库，刘 勇

（陕西通力专用汽车有限责任公司，陕西 宝鸡 722045）

目前某矿用车减震器杆件容易出现弯曲变形，且变形方向带有不确定性和弯曲变形的位置基本相同等特征的质量问题，经分析与压杆稳定失稳状态表现形式吻合，所以对减震器进行压杆稳定性探究，并给出减震器选型的几点校核意见。

减震器；压杆；稳定性

10.16638 /j.cnki.1671-7988.2016.10.023

CLC NO.: U472.4 Document Code: A Article ID: 1671-7988 (2016)10-69-03

前言

压杆稳定问题：压杆失稳——受轴向压力的长细杆，当压力达到某个限度时，轴线不能保持直线形状而发生突然弯曲的现象，称为压杆失去稳定性，简称失稳。

1、正常工况减震器稳定性校核

压杆保持直线稳定形状时所能承受的最大压力Pcr称为临界力。由欧拉公式知：

由失效形式和模型分析需要，仅对活塞杆部做稳定性分析。活塞杆直径20mm，活塞杆长度450mm。

减震器安装为两端铰接式安装，活塞、挺杆和桁架结构中的受压杆一般可以简化为两端铰支杆。 因此式（1）中的μ=1。

所以该杆件临界应力为：

λ——压杆的柔度，没有单位，反映长度、支座形式、横截面形状和尺寸等因素综合影响。

压杆越长（l↑），越细（d↓），λ就越大，故柔度又叫长细比。λ越大，临界压力就越小，越容易失稳。已知l=450mm，d=20mm，所以λ=90。

20钢材料弹性模量E=206GPa，材料比例极限σp=200MPa。所以λp≈100。

因此λ＜λp，所以欧拉公式不适用。又由于优质碳钢λs=60≺λ，该件不属于很小短柱脆性材质稳定性，我们暂不分析脆性材质的稳定性分析。

由此λp＞λ＞λs，符合欧拉经验公式

式中a和b是与材料性质有关的常数。查表知a=461 MPa，b=2.568 MPa。

表1 常用材料a和b数值

最大的复原阻力为16547N时，

由于上述结论是比较理想状态下的理论压杆模型计算，同时试验最大复原阻力的变化系数2～3，且工程应用中我们必须考虑杆件载荷偏心和杆件的初曲率对分析结果的影响。故需引入稳定系数ψ，ψ为柔度λ的函数，可由直线内插法求得，这里我们就不进行计算。参照机械设计手册对压杆稳定设计相关要求，我们将最大复原阻力变化系数和稳定系数考虑进来重新校核计算。

经查机械设计手册，轴心受压构件的稳定性经验公式：

表2 轴心受压构件的稳定系数φ值

查表得：ψ=0.669。

因此σ=78.8MPa

杠杆安全系数一般选择1.8～3，正常工况下符合设计要求。但实验显示16547为速度为0.52m/s时产生的。 由下图观察曲线走势，结合车辆运行情况，瞬间速度如果出现1m/s时力有可能翻倍。安全系数有可能<1存在隐患。

2、减震器失稳状态下的因素探究

在不考虑减震器卡滞等质量问题带来的不可预估的损坏问题，根据第一部分结论，从正常使用角度分析影响该减震器稳定性因素为临界力和直径。以下我们从减震器失稳的临界状态进行推理验证。

2.1 临界力因素

从目前使用情况，减震器的力主要来自板簧变形储能，板簧初始有预紧力，板簧压平后板簧储能相对为0，板簧反弓最大瞬时释放时是造成减震器受力最大的状态，所以我们仅考虑板簧反弓所造成板簧储备的力值。

临界力：F=σcr×ϕA =48290N （8）

（其中活塞杆直接d=20mm、σcr=229.88MPa、稳定系数ϕ=0.669）

板簧蓄力 FN=G×H =56800N （9）

式中板簧刚度G=710N/mm，板簧反弓高度H=80mm。

因FN>F，即板簧蓄力超过减震器失稳的临界值，造成减震器失稳。所以在板簧反弓到极限位置时，减震器液压油给活塞杆施加的反作用力早已使活塞杆失稳损坏。

接下来我们校核维持失稳临界力板簧能够被允许的反弓高度。

因此在上述速度范围内，板簧反弓小于68mm，d=20mm时活塞杆所受力使活塞杆处于稳定状态，不会被损坏。

2.2 直径因素

下面我们以80mm板簧反弓高度为基础，推导能够满足的截面直径。

按板簧反弓高度S=80时，FN=56800N 时计算，由于式中ϕ,AN,d ,σN都和λ有函数关系。考虑到机械设计手册中λ的取值为100,90,80,70,60.....如果已知直径推导出来的λ不在这几个数内，那么就必须进行繁琐的λ和ϕ的推导过程。为了简化计算，我们将λ和ϕ取以下值：

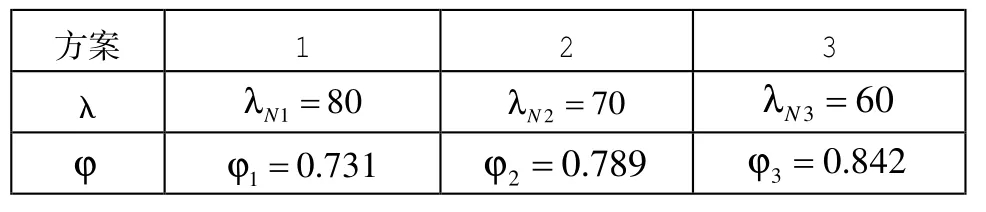
表3 λ和ϕ取值

以上是建立在板簧反弓最大后瞬间释放力计算，如果反弓最大被弹回等别的复杂情况出现可能不适用。所以建议安全系数大于等于2～3来消除该方面顾虑。

经计算如下：

表4 计算结果

对以上的分析得出以下结论：

1）d=20mm，板簧反弓高度S必须小于等于68mm结构才能稳定。

2）d≥22.5mm，板簧反弓高度S必须小于等于80mm，安全系数接近极限所以不建议采用该直径附近值。

3）d≥30mm，板簧反弓高度S必须小于80mm，正向和反向安全系数都符合要求且有一定盈余。并且杆件结构为粗短压杆，稳定性按强度条件计算。

3、经过以上分析我们得出以下几点参考意见

从传统意义压杆稳定推导需要注意力值的变化因素，且力值和瞬时速度有关，同时杆子直径和速度变化范围必须圈定，否则计算无意义。

从损坏的边界条件去判定和选杆子直径需要第一部分的理论支撑。反算中的直径和柔度计算相当复杂。文中只是选取部分之进行分段判定。

如果瞬时速度无法把握，又想得出特定状态下是否稳定需要逆向分段。

[1] 刘鸿文, 材料力学Ⅰ(第4版). 高等教育出版社, 2004.

A shock absorber strut bar stability inquiry

Kang Shuiku, Liu Yong
（ Shaanxi Tongli Special Vehicle Co., Ltd. Shaanxi Baoji 722045 )

Currently a mine car shock absorber rods prone to bending deformation, and the deformation direction with uncertainty and bending position substantially the same characteristics of quality problems, the analysis Buckling instability and state forms consistent, so shock absorber strut stability were explored, and give a few comments check damper selection.

shock absorbers; strut bar; stability

U472.4

A

1671-7988(2016)10-69-03

康水库，(1986-)，男，助理工程师，就职于陕西通力专用汽车有限责任公司，现担任陕西省专用车装备工程技术研究中心设计员，研就方向：主要从事是非公路驾驶室及相关零部件的设计工作。第二作者简介：刘勇，(1985-)，男，工程师，就职于陕西通力专用汽车有限责任公司，现担任陕西省专用车装备工程技术研究中心工艺所所长，研就方向：主要从事是重型商用汽车及特种自卸车零部件设计及工艺研究。