通信网络系统可信性测度模型

2016-11-20周森鑫韩江洪张耀辉李超

电信科学 2016年1期

关键词：马尔可夫多态网络系统

周森鑫，韩江洪，张耀辉，李超

(1.合肥工业大学计算机与信息学院，安徽合肥 230009;2.安徽财经大学管理科学与工程学院，安徽蚌埠233030)

通信网络系统可信性测度模型

周森鑫1，2，韩江洪1，张耀辉2，李超2

(1.合肥工业大学计算机与信息学院，安徽合肥 230009;2.安徽财经大学管理科学与工程学院，安徽蚌埠233030)

针对通信网络的安全性、可控性和可生存性的测度问题，采用连续时间多态有奖马尔可夫方法建立网络模型，定量分析其性能并构建可信性测度模型。提出了系统结构方程方法解决传统状态分析法中的“状态爆炸”问题。运用通用生成函数方法优化状态转换概率求解步骤，降低计算复杂度。实例仿真实验表明，计算模型正确、可行。

工业控制网络;可信网络;网络结构函数;通用生成函数;有奖马尔可夫链

1 引言

在传统的可靠性分析中，人们大多会把系统中元件的状态分为二元状态，即完全工作状态和完全失效状态。但现实系统中元件的状态不是只有两个状态，还有许多中间状态，这样的系统被称为多状态系统。多状态系统的可靠性理论被提出之后，受到国内外学者的关注，许多学者把多状态系统可靠性理论运用到诸如空调控制维护系统、工业系统寿命预估、发电系统等方面［1］。张小玲等［2］提出了一种基于通用生成函数的可靠性分析方法，这种方法首先用通用生成函数对离散型随机变量进行转化，然后用极大熵方法求极限状态函数的概率密度函数。最终基于通用生成函数的可靠性分析方法对负载进行分析，得出该方法既不需要求性能函数的导数，也不需要求最大可能点，适合于求解混合离散变量和高度非线性问题。江逸楠等［3］对网络可靠性评估方法进行了整理和综述，分析了二态、故障统计独立假设下新的精确算法，二态、故障统计独立假设下新的近似方法，考虑多态、共因故障的方法;并分析了网络可靠性在当时的问题。章筠［4］针对拓扑结构固定的多源多宿多态计算机网络，提出了一种可靠度最大化的网络传输线配置方法，在满足费用约束的情况下，极大化网络数据传输的可靠度。提出了一个基于最小路集的单条备用路径算法来评估单条工作路径失效情况下的网络可靠度。任博等［5］提出一种基于通用生成μ函数的液压系统可靠性分析新方法，并对某液压系统可靠性进行分析。和传统的蒙特卡洛仿真方法进行对比，避免了传统蒙特卡洛仿真方法拟合部件级不确定性概率分布的误差。柳剑［6］将复杂系统脆性理论与多状态制造系统理论相结合，提出一种基于脆性理论的多状态制造系统可靠性分析方法。分别定义了多状态制造系统及其设备单元的生成函数，对多状态制造系统的工作性能状态与实际稳态可靠度等指标进行了分析。李明程、何平［7］为解决传统通用生成函数不适用于多状态的瞬态模型的问题，提出了一种结合随机过程和通用生成函数的方法，使用Lz变换的方法进行实例分析。

本文借鉴上述研究成果，提出了一种基于多态有奖马尔可夫通信网络可信性的测量方法。用状态分析法分析通信网络不同层次的系统状态，运用有奖多态理论分别构建通信系统的安全性、可控性和可生存性模型。采用Howard微分方程组定量计算不同层次系统的安全性、可控性和可生存性量值。针对通信系统的硬件和软件组合的复杂性，运用通用生成函数理论提出通信网络系统的结构方程计算方法，计算整体及不同层级的系统的可信度。由于改进了传统可靠性理论中的二元状态理念，认为不同层次系统有多种状态更符合通信系统的本质特征。根据通信系统的历史数据借助大数据平台计算出其状态转移概率，可精确实时计算通信网络系统的可信度，为强化通信网络系统的安全性提供理论依据。

2 有奖多态马尔可夫通信网络可信度计算

2.1 网络模型建立

通信网络系统是由计算机系统和网络传输设备等若干个软硬件组件组成的非线性复杂系统。研究其可信需构建网络模型，用相关的随机过程理论定量计算其安全性、可控性和可生存性［8］。常用的方法是用状态分析法将网络系统按照网络组件二元理论的标准建立系统状态转换随机过程。

2.2 计算方法

为提高模型的理论和应用价值，需突破以往二态可靠性理论对系统和其组成单元的状态数量的限制。充分考虑网络的可控性和可生存性研究的有效方法，构建多态有奖马尔可夫可信通信网络模型。具体技术路线是运用结构函数刻画网络的结构特征，理清网络系统的核心功能，构建网络的安全关键核心态，并以此为网络可信基。基于性能参数对系统和其组成单元的状态划分为多态，运用多态理论和有奖连续时间马尔可夫理论定量研究系统的安全性、可控性和可生存性［9-13］。归一处理后得出可信度，根据可信度的量化值将网络系统划分为若干个可信等级。技术路线如图1所示。

图1 技术路线

3 多态理论与网络结构函数

3.1 多态理论

传统可靠性理论中，系统被假设为二元系统。对复杂系统过于简单，不能真实地反映实际情况。近来年，多状态可靠性理论的研究已成为可靠性领域的热点问题。多态系统主要分为两种:多工作状态系统和多性能水平系统。多工作状态系统是指系统除了“正常工作”和“完全失效”两种状态外，还具有多种工作状态，如传统可靠性领域的k/n(G)系统;多性能水平系统是指系统能够在多种性能水平下运行。对于可信通信网络系统同时具有两种系统特征，多工作状态系统对应于系统的可控性，多性能水平系统对应于系统的可生存性。

设多态系统有 M 个状态，其状态空间表示为｛1，2，3，…，M｝，其中 M＞2，M 是正常态，1表示失败态;当M=2时，为传统的二态系统。对于多工作状态系统，用状态空间和状态概率描述其特性，其中状态概率表示系统处于各种状态的概率;对于多性能水平系统，用状态性能和状态概率描述其特性，其中状态性能表示系统处于各种状态时的系统性能水平。多态系统可靠性分析方法主要有4种:布尔模型扩展方法、随机过程方法 (主要是Markov过程方法)、Monte Carlo仿真方法和通用生成函数(universal generating function，UGF)方法。由于传统可靠性理论中部件和系统只有两种状态，而多态系统中部件和系统具有多种状态，因此，在最初分析多态系统可靠性时，尝试对布尔模型进行扩展，以满足分析多态系统可靠性的需要。布尔模型扩展方法主要包括多态故障树、多态路集和割集、多值逻辑理论、决策图等方法;随机过程中的Markov过程方法在多态系统可靠性分析中的应用相对较多，Markov过程方法的优点是能够获得系统可靠度与时间的关系，且理论成熟。布尔模型扩展方法、随机过程方法和Monte Carlo仿真方法由于计算复杂，主要适用于规模较小的多态系统;而通用生成函数方法计算速度快，且便于数值实现［14，15］。

3.2 网络结构函数

通信网络系统是由计算机硬件、软件和网络传输设备组成的复杂系统，涉及硬件、软件和网络协议。需用层次分析法从应用层自顶向下分别建立子系统及其结构函数，利用递归求解方法得出网络系统的可信度。将网络系统组件的性能空间映射到系统性能空间的变换f(G1(t)，…，Gn(t)):Ln→M，叫做网络结构函数。也可以把结构函数表示为G(t)=f(G1(t)，…，Gn(t))。如从应用层分析网络系统时，可将网络系统划分为应用软件系统、操作系统、网络传输、硬件等子系统，其结构函数为串行结构。结构函数分为串行、并行、桥式、表格和k/n(G)类型，常用的有串行、并行和 k/n(G)3种。示例如图1～图3所示。

图2的网络系统的结构函数为:

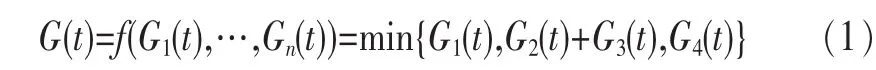
图3的网络系统的结构函数为:

图2 网络结构函数示例1

图3 网络结构函数示例2

k/n(G)的结构函数如下:

k/n(G)系统需根据具体情况进行分析。

3.3 通用生成函数

通用生成函数(UGF)是一种简洁、高效的离散随机变量组合运算工具。其基本思想是将离散随机变量表示为多项式形式，根据离散随机变量的运算法则定义多项式的组合算子，通过递归运算得到最终结果的离散随机变量的多项式形式。通用生成函数法是一种基于 Z变换和组合算子的运算方法。通用生成函数依赖于简单直观的递归方程，并且提供了系统状态枚举的系统方法，可以替换极其复杂的组合运算。

设离散型随机变量 x的所有取值X=(X1，X2，…，Xk)与其相对应的概率值为p=(p1，p2，…，pk)，则x的生成函数为:

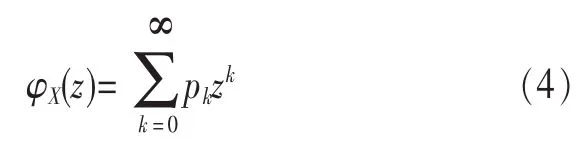
根据离散型随机变量x1，x2，…，xn中的Z变换多项式可确定任意函数 f(x1，x2，…，xn)的概率密度函数(PDF)。如随机变量函数 Y=f(x1，x2，…，xn)，通用生成运算符为 Ωf，随机变量 Y的通用生成函数定义为:

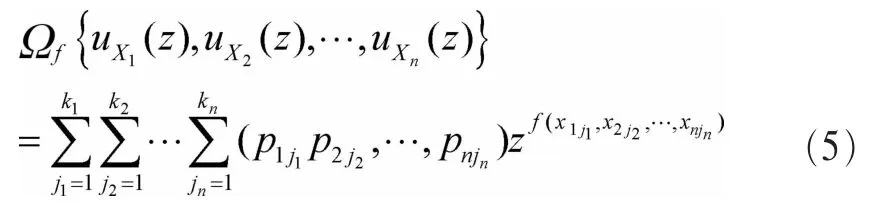
其中，piji是离散随机变量 xi取值为 Xiji的概率［16］。

3.4 连续时间有奖马尔可夫链

设随机过程｛X(t)，t≥0｝，状态空间 I=｛in，n＞0｝，若对任意

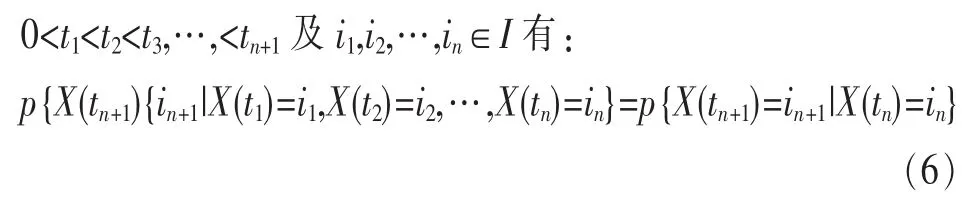
则称｛X(t)，t≥0｝为连续时间马尔可夫链。系统的状态转移概率是在初始时刻s处在状态i，经过时间t后转移到状态j的概率，可表示为:

如果系统的状态转移概率pi，j(s，s+t)和s无关，随机过程｛X(t)，t≥0｝称为连续时间的齐次马尔可夫链，并满足以下连续性的条件:

对于任意 t≥0，有:

其中，pi(t)是｛X(t)，t≥0｝的绝对分布，pi(0)是｛X(t)，t≥0｝的初始分布，使用全概率公式可以证明出:

因此，连续时间马尔可夫链的绝对分布完全由其随机过程初始状态和转移概率函数决定。有奖马尔可夫链是在连续时间马尔可夫链的基础上，在每个状态上分配一个单位时间奖励值，具体的物理意义可以是网络性能参数。假设系统在状态i上以每单位时间rii的速率获得奖励，其次假设系统从状态i转移至状态j(i≠j)，获得的奖励值为rij。

需要求解的是在给定初始条件下，经过时间t，系统的预期收益，即奖励率的时间累积。设vi(t)为系统在初始状态i下，经过时间t所获得的预期总奖励，根据递推公式就可以求出系统在时间t+dt内，获得的预期总奖励Vi(t+dt)。其中dt表示时间区间。

在时间dt内，系统可能保持状态i或者转移到状态j。如果经过时间dt，系统仍处于状态i，那么总收益为riidt与Vi(t)之和，并且经过时间dt处于状态i的概率为1减去系统在时间dt发生状态转移的概率，也就是另一方面，系统在时间dt内有aijdt的概率转移到状态j(j≠i)。在这种情况下，系统将获得的奖励值为rij与vj(t)之和。

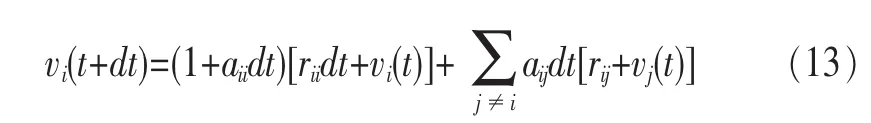
或者表示为:

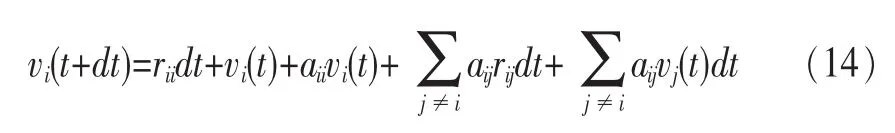
这里只考虑一次积分dt。最后，通过公式变换，可得到:

如果dt趋向于0，可得到Howard微分方程组为:

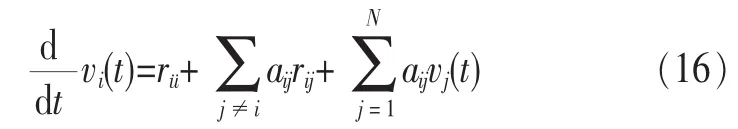
其中，i=1，2，…，N。

3.5 系统、子系统(元件)可信值的计算

网络通信系统根据安全需求目标的不同，可信计算量值的网络性能参数也不同。例如，在串行系统中对核心设备可生存性进行冗余设计时，关心的是子系统的可靠性。本文基于特定时间内可用性、失败次数、平均失效时间和可靠性4个性能参数进行可信值计算。

3.5.1 基于可用性可信值的计算

基于可用性可信值的计算方法是指系统可工作在多种不同性能状态，根据性能不同划分为可接收态和不可接收态。设G(t)是需求性能指标，W(t)是实际工作指标，函数Φ(G(t)，W(t))＞0 时，系统为可接收状态;当Φ(G(t)，W(t))＜0时，系统为不可接收状态。假设A(t)是t＞0时系统为可接收状态的概率，表示为:

系统的平均可用性A (T)是系统处在可接收状态［0，t］期间可用性的时间平均值，表示为:

为了计算系统的A (T)，奖励矩阵R的奖励值按下列规则确定:所有可接收态的奖励值为1;所有不可接收态和状态转移奖励值为0。

设状态K为初始状态(可接收状态)，求解Howard微分方程组，得到VK(T)。系统平均可用性为:

3.5.2 基于失败次数可信值的计算

基于失败次数的可信值是指系统在一段时间［0，t］内的平均失败次数。设系统的初始状态为正常态K，Nf(t)为系统在时间［0，t］内的平均失败次数，Nf(t)可视为［0，t］内系统状态由可接收态到不可接收态的次数。奖励矩阵R的奖励值按下列规则确定:系统从可接收态到不可接收态的奖励值为1;其他的奖励值为0。

通过Howard微分方程组求解VK(T)，可以得到在时间［0，t］内系统进入不可接收状态的平均次数［17］。

3.5.3 基于平均失效时间和可靠性可信值的计算

平均失效时间(mean time to failure，MTTF)是系统第一次进入不可接收态的平均时间。为了计算MTTF，定义从不可接收态返回的所有过渡态都被禁止，不可接收态被视为吸收状态。奖励矩阵R的奖励值按下列规则确定:所有可接收态的奖励值定义为1;不可接收态和转换的奖励值定义为0。

设初始状态为正常态K，通过Howard微分方程组求解 VK(T)，可以得到MTTF。

可靠性是指系统、子系统(元件)在［0，T］内正常工作的概率。计算可靠性时同样定义不可接收态返回的所有过渡态都被禁止，不可接收态被视为吸收状态。奖励矩阵R的奖励值按下列规则确定:所有过渡到吸收态的奖励值定义为1;其他的奖励值为0。

设初始状态为正常态K，通过Howard微分方程组求解VK(T)，可以得到可靠性函数R(T):

4 算例分析与实验仿真

4.1 实验仿真环境

SHARPE(层次自动化的可靠性和性能评估)是美国杜克大学Trivedi教授及其科研团队开发的一种层次法定量计算可靠性、可生存性和可用性等系统性能的软件仿真环境。它是多态有奖马尔可夫链应用建模技术的很好的工具，并支持多态理论模型。支持系统组件行为和功能对系统结构的影响，整个系统的行为作为一个时间的函数。系统结构可以被指定，如故障树、任务图、马尔可夫链和有奖马尔可夫链。Howard微分方程组的求解可用Maple或MATLAB软件编程实现。

4.2 算例分析

设某网络系统中有3个通信服务器组成的数据传输子系统，任务是将以太网1的数据传输给以太网2，其系统结构如图4所示。

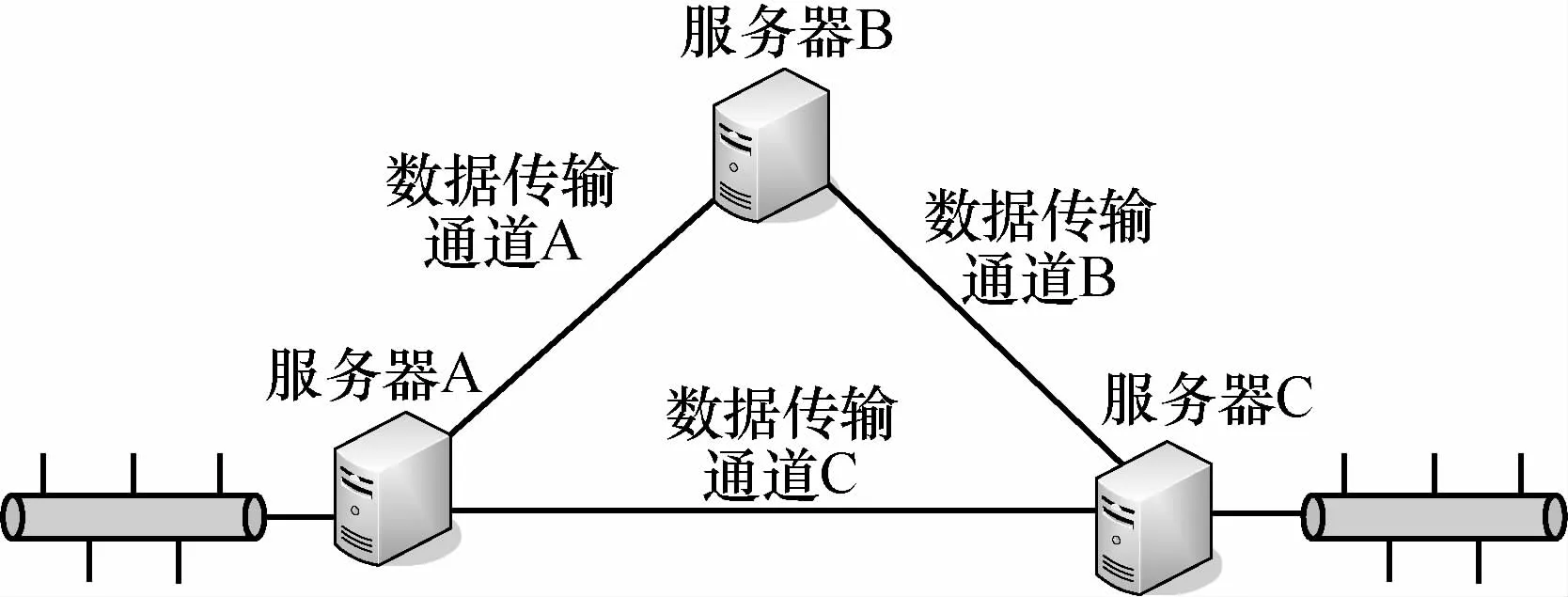
图4 算例系统结构

数据可以通过服务器A从服务器B传输到服务器C或直接从服务器A传输到服务器C。服务器之间的数据传输时间(即通道性能率，以ms为单位)取决于相应的通信信道。其中A到B组成数据传输通道A，B到C组成数据传输通道B，A到C组成数据传输通道C。数据传输通道A和B是二元状态，处于完全故障状态时数据不能传输，在这种情况下，数据传输时间定义为∞;处于完全运行状态时，传输数据的时间分别为1.5 ms和2 ms，分别表示为:G1(t)=｛∞，1.5｝，G2(t)=｛∞，2｝。数据传输通道 C 有 3 种状态:完全故障状态、部分故障状态(数据传输时间为4 ms)和正常工作状态(数据传输时间为1.8 ms)，表示为G3(t)=｛∞，1.8，4｝。子系统性能定义为数据从服务器A传输到服务器C的总时间。

当通过服务器B传输数据时，数据传输的总时间等于数据从服务器A到服务器B所用时间G1(t)和从服务器B到服务器C所用时间G2(t)的总和。当数据直接从服务器A传输到服务器C时，传输时间是G3(t)。数据传输通道A和B是传统的二元状态，而数据传输通道C是三元态(即多态)。该系统结构由3个数据传输通道组件组成，数据传输通道A和B先构成串行结构再和C组成并行结构。其结构函数为［18］:

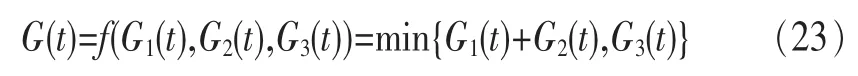
按传统的状态分析法，以组件性能参数为指标划分系统状态，得出系统状态图如图5所示。

图5 系统状态分析图

其中，状态10、11和 12为不可接收态，状态 4、5和 6是性能中间态，其他为性能良好态。由此可见，随着组件个数和性能等级的增加，状态数会指数级增加，从而产生“状态爆炸”问题。根据结构方程和生成函数可将图5化简为4个状态。状态1为子系统数据传输时间为1.8 ms，状态2为子系统数据传输时间为3.5 ms，状态3为子系统数据传输时间为4 ms，状态4为子系统数据传输时间为∞。化简后的状态及其转换关系如图6所示。

图6 多态系统分析

参数λ和μ为状态转移率，通过历史数据可收集到。子系统的3个数据传输通道(组件)状态的初始概率分布pi和网络性能参数xi的值见表1。

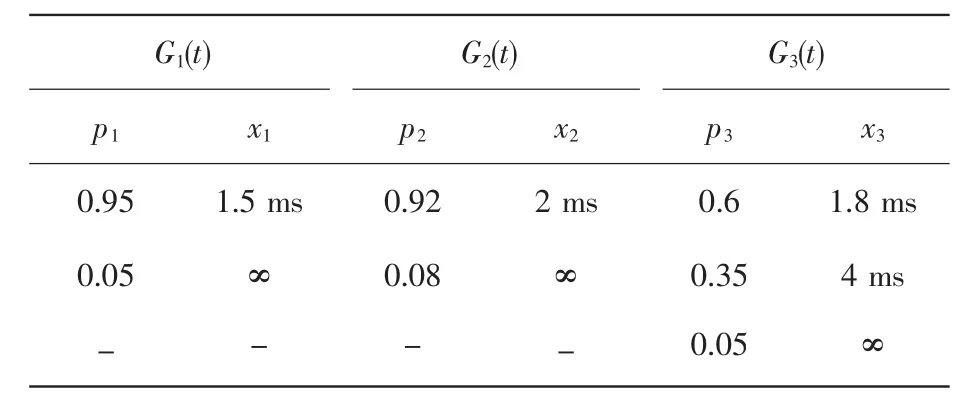
表1 系统的状态概率密度的随机变量

概率密度函数可由如下通用生成函数确定:

因为所求的是关于速度的最小值，可以得出:

假设一个G4(t)，定义G4(t)值如下:

可以通过通用生成函数得到系统概率密度函数的分布Y:

因此子系统的初始概率密度分布和数据传输性能为:

求解子系统可信动态模型可构建马尔可夫链，即求解由3个数据传输通道构成的子系统网络传输性能与时间的函数。假设通过历史数据处理得到各状态转移率矩阵如下:

其中，c1=-(λ12+λ13+λ14)，c2=-(μ21+λ23+λ24)，c3=-(μ31+μ32+λ34)，c4=-(μ41+μ42+μ43)。

由柯尔莫哥洛夫向后方程:

可求出转移概率矩阵P(t)。由转移概率矩阵P(t)和初始状态概率分布，可计算子系统的动态状态分布。动态状态分布表明，系统的实际工作性能并不能确定其完成任务的能力(即可信)。为了计算可信性能还要考察完成任务的能力［19］。

假设子系统的数据传输时延性能指标为W1=2 ms，W2=3.9 ms，W3=4.5 ms。不考虑断路情况，子系统的实际数据传输时延性能为 G1=1.8 ms，G2=3.5 ms，G3=4 ms。子系统实际性能是多状态连续时间马尔可夫链，子系统的数据传输时延性能指标也是多状态连续时间马尔可夫链。它们的状态转换分别如图7、图8所示。

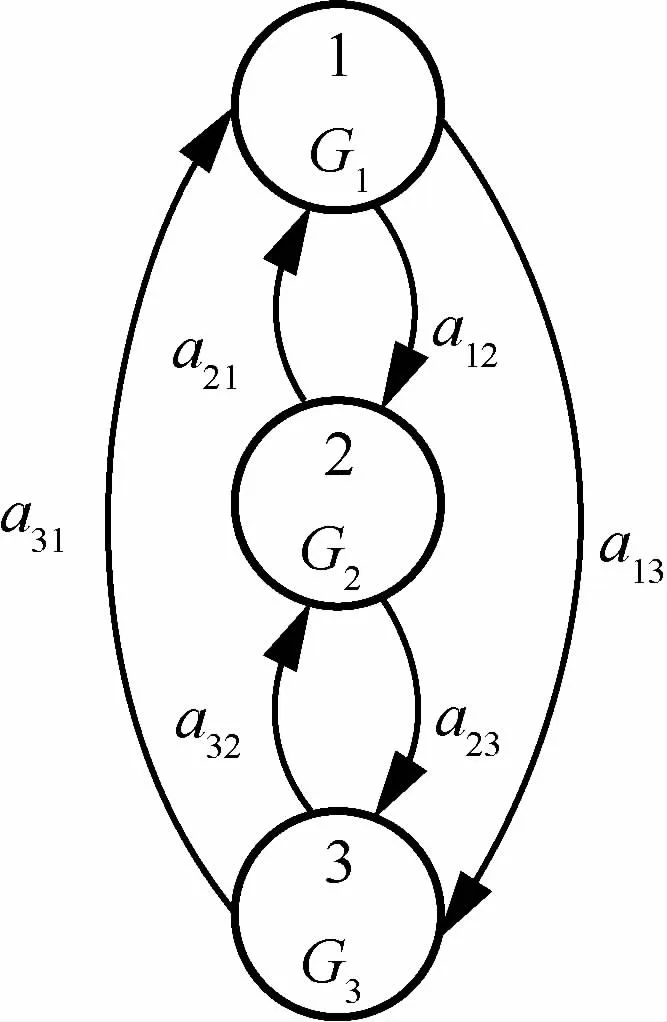
图7 数据传输能力状态

图8 数据传输指标状态

因为性能指标具有实时性，选择可信函数Φ(G(t)，W(t))＜0，即实际传输时延要小于指标时延。结合性能指标的系统状态及其转移情况如图9所示。

图9中状态2、3、6为不可接收态，其余为可接收态。系统的状态转移矩阵C为:

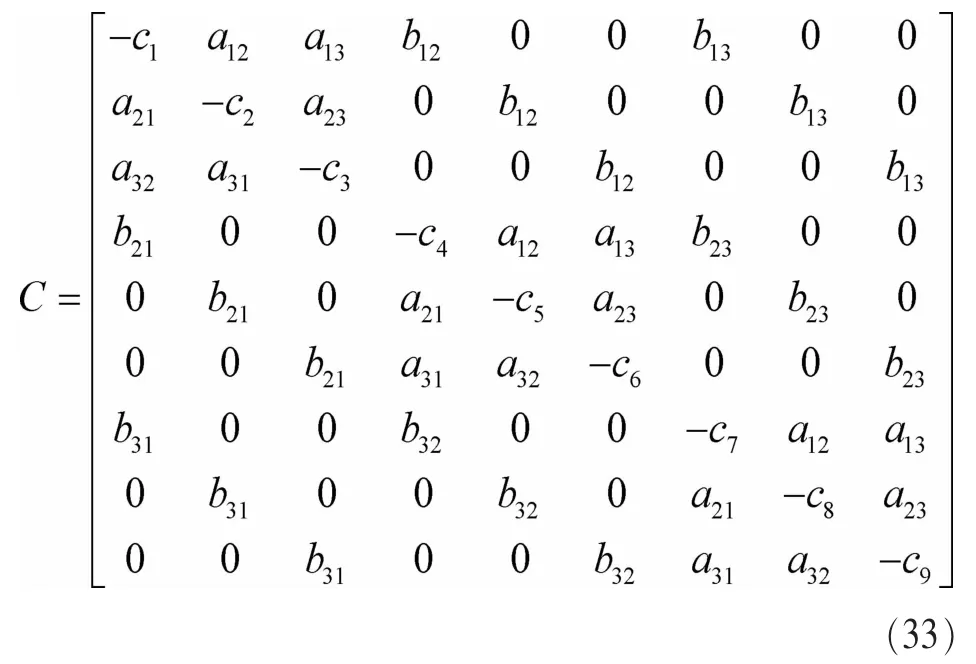
其中:

假设通过历史数据收集，数据传输实际能力转移率矩阵A和数据传输指标转移率矩阵B数值如下。

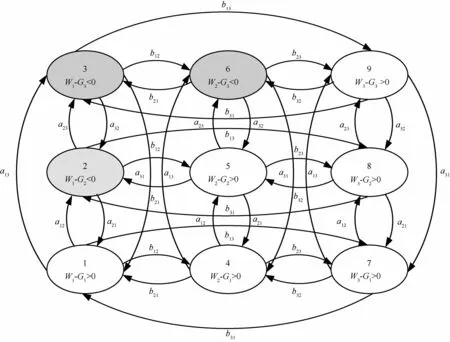
图9 结合性能指标数据传输状态图

根据矩阵A和矩阵B可求得结合性能指标数据传输状态图的转移率矩阵C。

按照计算可用性奖励矩阵设置方法，设置奖励矩阵R。

将矩阵C和R代入Howard微分方程组式(16)，假设状态1为初始状态，求解方程组可得V1(t)/t，即数据传输通道的平均可用性。分别按照平均失效时间、［0，t］内失败次数和可靠性的相关原则设置相应奖励矩阵，可得到相应的Howard微分方程组。假设系统的初始状态为状态1，求解微分方程组求得V1(t)，可分别得到系统的平均失效时间、［0，t］内失败次数和可靠性。可用性Howard微分方程组如下:

图10 系统平均可用性

其他Howard微分方程组不再赘述，编程通过MATLAB软件求解，系统平均可用性如图10所示。

仿真结果和计算结果完全一致。由图10中可以看出，当时间大于1时可用性恒等于7，因此系统可生成性大于7。系统的安全性和可控性由状态转移率确定，如安全性主要反映在从可接收态转移到不可接收态的转移率的大小，而可控性反映在从正常工作态到不可接收态的转移路径及其转移率的大小。其他性能参数与时间关系如图11～图13所示。

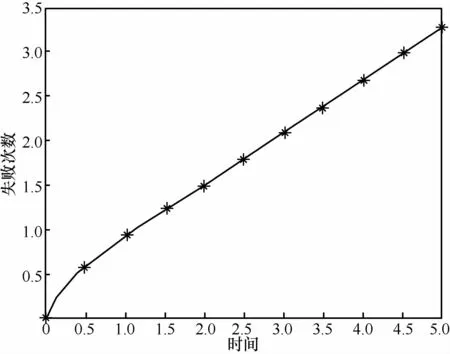
图11 系统失败次数

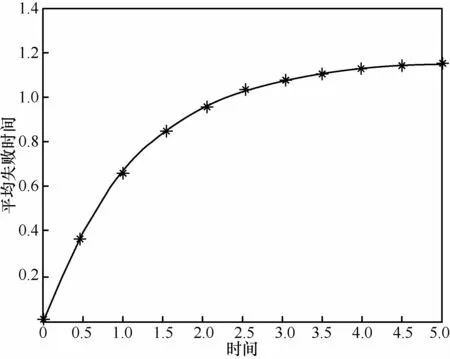
图12 系统平均失效时间

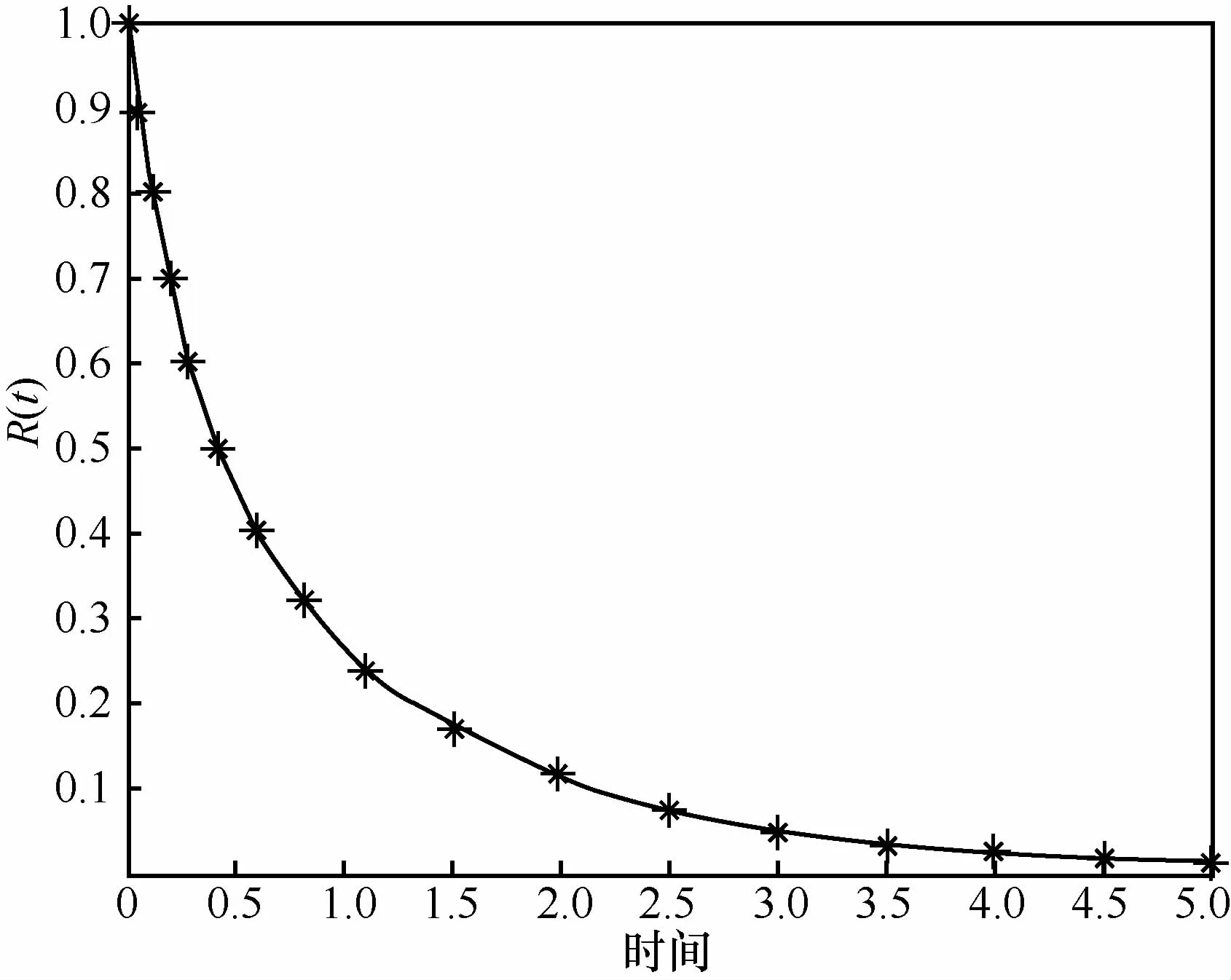
图13 系统可靠性

5 结束语

沿着“可信≈安全+可靠”思想将通信网络的可信属性分为安全性、可生存性和可控性。按照自顶向下逐渐求精的原则建立系统状态模型，由元件(子系统)的可用性、可靠性和可生存性等性能参数，利用通用生成函数计算系统的概率分布，通过结构方程约简系统状态，避免“状态爆炸”问题。上述算法递归调用可求出不同层级的网络系统性能参数，即系统实际性能。网络系统实际性能是多状态连续时间马尔可夫链，而网络需求性能指标也是多状态连续时间马尔可夫链，通过可信目标函数如 Φ(G(t)，W(t))＞0划分可接收态和不可接收态，根据网络需求情况分别设立奖励矩阵，建立多态有奖马尔可夫通信网络系统可信模型。该模型能定量动态表达通信网络系统完成任务的能力，然后根据所得量值按照可信标准将网络系统划分为不同的可信等级［20］。

［1］LEVITIN G.The Universal Generating Function in Reliability Analysis and Optimization ［M］.London:Springer Series in Reliability Engineering，2005:1-25.

［2］张小玲，黄洪钟，肖宁聪，等.基于通用生成函数的可靠性分析方法［J］.机械设计，2011，28(11):93-96.ZHANG X L，HUANG H Z，XIAO N C，et al.Reliability analysis method based on universal generating functions ［J］.Mechanical Designing，2011，28(11):93-96.

［3］江逸楠，李瑞莹，黄宁，等.网络可靠性评估方法综述［J］.计算机科学，2012，39(5):9-18.JIANG Y N，LI R Y，HUANG N，et al.Survey on network reliability evaluation methods［J］.Computer Science，2012，39(5):9-18.

［4］章筠.计算机网络可靠性分析与设计［D］.杭州:浙江大学，2012:3-25.ZHANG Y.Reliability analysisand design forcomputer network［D］.Hangzhou:Zhejiang University，2012:3-25.

［5］任博，吕震宙，李贵杰，等.基于通用生成函数的系统寿命可靠性分析［J］.航空学报，2013，34(11):2550-2556.REN B，LV Z Z，LI G J，et al.Reliability analysis for system life based on universal generating function［J］.Acta Aeronautica at Astronsutica Sinica，2013，34(11):2550-2556.

［6］柳剑，张根保，李冬英，等.基于脆性理论的多状态制造系统可靠性分析［J］.计算机集成制造系统，2014，20(1):155-164.LIU J，ZHANG G B，LI D Y，et al.Reliability analysis for multi-state system based on brittleness theory ［J］.Computer Integrated Manufacturing Systems，2014，20(1):155-164.

［7］李明程，何平.基于Lz变换的多性能参数系统可靠性分析［J］.统计与决策，2015，426(6):20-23.LI M C，HE P.Reliability analysis for multi-parameter systems based on Lz transform ［J］.Statistics&Decision，2015，426(6):20-23.

［8］OKHRAVI H，NICOL D M.Application of trusted network technology to industrialcontrolnetworks ［J］.International Journal of Critical Infrastructure Protection，2009(2):84-94.

［9］林闯，彭雪海.可信网络研究［J］.计算机学报，2005(5):751-758.LIN C，PENG X H.Research on trustworthy networks ［J］.Chinese Journal of Computers，2005(5):751-758.

［10］沈昌祥，张焕国.信息安全综述［J］.中国科学 E 辑，2007，37(2):129-150.SHEN C X，ZHANG H G.Overview of information security［J］.Science in China(Series E:Information Sciences)，2007，37(2):129-150.

［11］郑君杰.可信网络关键问题研究［J］.电信科学，2010，26(2):55-59.ZHENG J J.Research on key problems for trusting network［J］.Telecommunications Science，2010，26(2):55-59.

［12］邓建春.可信网络的信任模型研究［D］.成都:电子科技大学，2013:15-25.DENG J C.Research on trust model in trusted network ［D］.Chengdu:University of Electronic Science and Technology of China，2013:15-25.

［13］闫小侠.可信网络框架研究与设计［D］.北京:北京工业大学，2014:15-35.YAN X X.Thetrustednetwork frameworkresearch and design［D］.Beijing:Beijing University of Technology，2014:15-35.

［14］肖跃雷.可信网络连接关键技术研究及其应用［D］.西安:西安电子科技大学，2013:20-36.XIAO Y L.Research on key technologies of trusted network connect and their application ［D］.Xi'an:Xidian University，2013:20-36.

［15］刘宇.多状态复杂系统可靠性建模及维修决策［D］.成都:电子科技大学，2010:25-38.LIU Y.Multi-state complex system reliability modeling and maintenance decision ［D］.Chengdu:University of Electronic Science and Technology of China，2010:25-38.

［16］李春洋.基于多态系统理论的可靠性分析与优化设计方法研究［D］.长沙:国防科学技术大学，2010:32-45.LI C Y.Research on reliability analysis and optimization based on themulti-statesystem theory ［D］.Changsha:National University of Defense Technology，2010:32-45.

［17］LISNIANSKI A.The Markov reward model for a multi-state system reliability assessment with variable demand ［J］.Quality Technology&Quantitative Management，2007，4(2):265-278.

［18］LEVITIN G.The Universal Generating Function in Reliability Analysis and Optimization ［M］.London:Springer Series in Reliability Engineering，2005:32-65.

［19］LISNIANSKI A，FRENKEL L，DING Y.Multi-state System Reliability Analysis and Optimization for Engineers and Industrial Managers ［M］.New York:Springer London Dordrecht Heidelberg，2010:32-67.

Trusted measure model for the communication network system

ZHOU Senxin1，2，HAN Jianghong1，ZHANG Yaohui2，LI Chao2
1.School of Computer and Information，Hefei University of Technology，Hefei 230009，China 2.School of Management Science and Engineering，Anhui University of Finance&Economics，Bengbu 233030，China

The trusted measure model for communication was proposed by computing its value of security，control and survivability with continuous-time reward Markov method.The “state bomb” problem in traditional state analysis method was solved by the way of structural equation solution.The generic function optimization algorithm was used to reduce computational complexity.Simulation experiments show that the model is correct and feasible.

industrial control network，trusted network，network structure function，universal generating function，reward markov chain

TP302.7

10.11959/j.issn.1000-0801.2016010

2015-10-15;

2015-12-15

周森鑫(1965-)，男，博士，安徽财经大学教授、硕士生导师，主要研究方向为计算机网络、计算机控制、可信计算、数据挖掘。