基于随机森林模型的房价预测

陈世鹏　金升平

摘 要：根据襄阳2012年的房贷数据，考虑影响房价的各种特征变量，尝试建立随机森林模型，利用其优秀的集成学习能力和泛化能力对测试样本进行房价预测，并与学者应用较多的ARMA模型及经典的多元线性回归模型预测的房价和实际房价进行对

比，取得了较好的效果。

关键词：随机森林；房价；ARMA模型；多元线性回归模型

1 传统的房价预测模型简介

1.1 ARMA模型

ARMA即自回归滑动平均模型，是研究时间序列的重要方法，可以研究并预测房价随时间的变化，由AR（Auto-Regressive）和MA（Moving-Average）两个部分组成，若时间序列yt服从（p，q）阶的ARMA模型，则其满足形式为：

1.2 多元线性回归模型

多元线性回归模型经常用来刻画一个变量受多个变量影响时的情况，适用于自变量与因变量之间呈现密切的线性相关且自变量之间具有一定的互斥性的情形，其基本模型如下：

2 随机森林模型的建立

2.1 随机森林建模的步骤

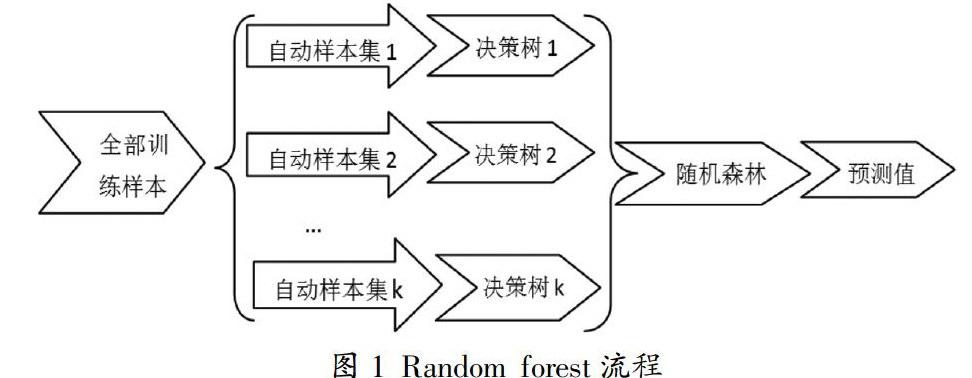
随机森林在建立模型及预测的流程如图1所示：

其基本思想是通过自助法重采样技术从原始训练样本集中抽取样本生成新的训练样本集合，由此生成多棵决策树组成随机森林，分类数采取投票方式、回归数利用均值来进行结果预测，具体步骤为：（1）确定生成一棵决策树时用到的特征变量个数m（

助样本集，并由此构建K棵决策树，每次未被抽到的样本组成k个袋外数据，即out-of-bag（OOB）；（3）每个自助样本集生长为单棵决策树，每个节点处按照节点不纯度最小原则选取特征进行充分生长，不进行剪枝操作；（4）根据生成的决策树分类器对预测集进行预测，对每棵树的预测结果求均值即为最终预测结果[3]。

2.2 模型的建立与优化

整合2012年襄阳房贷数据，得到6354条有效数据，其中特征变量有房子所在楼层、总楼层、所在区域、房子面积、交易时间等，解释变量为每平方米单价（千元）。以总数据的75%作为训练集构造随机森林，剩下的25%数据作为测试集用来检验模型。每次抽取若干数据和特征变量，以信息增益或基尼指数作为衡量标准来选择节点处特征，然后进行充分生长构建决策树。

随机森林中最重要的两个参数有树节点预选的特征变量个数、随机森林中决策树的个数。特征变量个数决定了每棵树的规模，太多会导致每棵决策树差别不大，产生过拟合现象；太少则不能从数据中有效学习模型。同理，決策树数量太多会浪费很多时间进行计算，太少则预测效果很差。

图2中a图是利用R语言计算的默认的特征变量个数为1时的绝对累积误差和，可以发现当决策树的数量大于150以后，模型累积误差趋于稳定；对特征变量的个数进行遍历，可以发现预选个数为2时误差和最小，如b图所示。

3 预测结果的对比

根据整合的房贷数据，由训练集建立模型，利用测试集来对房价进行预测，随机森林与传统的ARMA模型和多元线性回归模型预测的部分房价（单位：千元/平方米）数据如表1所示。

4 结果分析

由预测结果可以看出，随机森林模型取得了较好的预测效果，基于OOB数据和测试集数据的绝对误差均值分别为大约0.08（千元/平方米）和0.2（千元/平方米），相对误差分别只有1.6%和4%，虽然上述预测结果相对于ARMA等传统模型优势并不明显，这是由于文章采用的数据特征变量数较少所导致的。实际中影响房子价格的可能还有小区的停车位、环境、运动设施、物业管理费用，周边的交通如公交线路、地铁线路的数量，到医院、学校、银行、商场、菜市场、CBD的距离等因素[4]，随机森林的优势在当特征变量数增加时会更加明显，其预测精度会进一步提升。

参考文献

[1]常振海，刘薇.基于非参数自回归模型的房价预测[J].天水师范学院学报，2010，3（2）：56-58.

[2]刘忠璐.ARIMA模型在房价预测中的应用[J].决策与信息，2011（4）：3-4.

[3]黄文，王正林.数据挖掘：R语言实战[M].电子工业出版社，2014：220-241.

[4]孙宪华，张臣曦.房屋质量及其对房地产价格指数的影响[J].统计与信息论坛，2009（9）：43-47.

作者简介：陈世鹏，男，武汉理工大学硕士，研究方向：最优化理论与计算。

金升平，男，教授，硕士生导师，研究方向：金融统计计算与随机模拟。