非线性振荡分析在土石坝变形监测资料的应用研究

陈国强，王 宇，谷艳昌，3，王 宏，3

（1.宜兴水务集团有限公司，江苏宜兴214206；

2.水利部交通运输部国家能源局南京水利科学研究院，江苏南京210029；3.水利部大坝安全管理中心，江苏南京210029）

非线性振荡分析在土石坝变形监测资料的应用研究

陈国强1，王 宇2，谷艳昌2，3，王 宏2，3

（1.宜兴水务集团有限公司，江苏宜兴214206；

2.水利部交通运输部国家能源局南京水利科学研究院，江苏南京210029；3.水利部大坝安全管理中心，江苏南京210029）

传统的时间序列法是对土石坝变形观测量在特定时间范围内的变化特征进行拟合建模，无法揭示观测点变形测值之间的共性。采用分形理论中非线性振荡分析方法，研究了变形时间序列数据的相关性及后续建模选取数据的有效性，提出的定标指数可用来甄别监测点时间序列的位移值是否存在长期记忆性，有效的预测未来的发展趋势，并指出后续建模选取时间序列的起始范围。实例应用结果表明提出的方法可较好的分析土石坝变形性态及预测预报，为土石坝变形安全分析提供了一种新途径。

土石坝；安全监测；变形；分形理论；非线性振荡分析

土石坝安全监测中，位移、渗流、应力等物理量是时间序列数据，体现了水位、温度、时效等综合效果，反映出大坝结构非稳态、高度非线性的动态特性［1-3］。传统时间序列法分析土石坝变形监测资料，采用外推的方法，用具体的观测值在某一时间范围内变化特征的基础上进行拟合建模，并预测监测点未来的发展趋势；当时间序列数据发生变化时，传统模型需要做一定的调整，不能揭示观测点变形测值之间的共性［4］。

分形理论可以描述自然界和人类生活中非线性动力系统的复杂性与随机性，揭示隐藏于大量复杂混乱现象中的普遍规律及其本质［5-8］。基于分形理论的非倾向性振荡分析（DFA）方法，将内在的严格自相似检验代入到形式上的非稳定时间序列，因而有效的避免了表面上自相似的虚假检验，该方法已经成功地应用于解决物理学、经济学、测绘科学等众多领域中与时间序列有关的问题［9-13］。文中将非线性振荡分析方法引入到土石坝变形监测资料分析中，揭示土石坝变形内在动态变化特征，并预测未来发展趋势。

1 非线性振荡分析

Peng（1994）在研究脱氧核糖核酸（DNA）的时间序列长期相关性时，首先提出了非线性振荡分析方法。与传统Hurst指数理论分析方法相比，非线性振荡方法优点是能够稳健地检验非平稳的时间序列，避免时间序列短程相关和非稳健性可能存在的虚假长期相关［14-15］。国内外学者已经将非线性振荡方法应用到多个领域，用来分析和检测非平稳时间序列。该方法分为以下五个步骤：

（1）变换时间序列｛xi｝，i=1，2，…，n，生成累积和序列。

（2）将时间序列y（k）分割成ns=［n/s］个互不重叠的子区间，每个子区间里有s个观测值；由于时间序列长度一般不是分割跨度s的整倍数，为避免遗漏最后剩余部分的时间序列，将序列y（k）末端往回再次分割；两次分割后共有2ns个等长子区间。

（3）采用最小二乘法拟合时间序列长度为s的子区间v内的时间数据，分别计算2ns个子区间的方差。

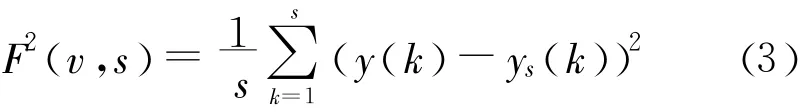
式中：F（v，s）为标准差；ys（k）为线段y的坐标。

（4）对所有部分取平均，计算方根得到非线性振荡波动函数F2（s）。

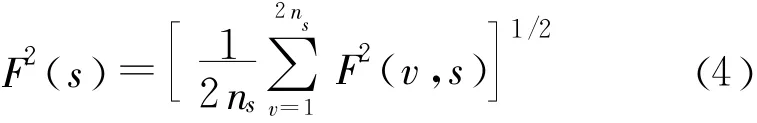
（5）对不同的s（3≤s≤［ns/4］），重复第（2）步，得出F（s）与s的关系式。在双对数坐标图下，如果F（s）与s存在严格或近似线性关系，那么存在一个幂律关系函数形式的波动Fs∞sα，即Fs=Csα。两边取对数得：

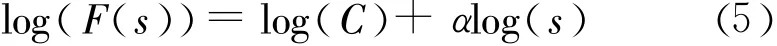
对式（5）用最小二乘线性拟合，求得直线斜率α，得到非线性振荡分析指数，即定标指数；基于定标指数α，观测序列的趋势性判别如下：当0＜α＜0.5时，表明时间序列具有反持续性，即观测量时间序列在各时间尺度上是负相关，这是一种负反馈机制；当α=0.5时，表明时间序列是随机游走的，未来的增量与过去增量不相关，即观测量时间序列在各时间尺度上是完全独立，随机变化的；当0.5＜α＜1时，表明时间序列具有持续性，即观测量时间序列在各个时间尺度上是正相关或长相关，这是一种正反馈机制。

2 实例应用研究

某水库总库容1.12×108m3，是一座以防洪、供水、灌溉为主，结合水产养殖、发电和第三产业等综合利用的大（2）型水库。水库工程等级Ⅱ等，大坝为2级建筑物。水库正常蓄水位为35.00 m；设计洪水位为38.75 m；校核洪水位40.36 m。

水库枢纽主体工程由一座主坝、两座副坝、泄洪闸以及输水涵洞组成。主、副坝皆为均质土坝，坝顶高程均为42.10 m，大坝总长4 090 m，最大坝高24.10 m，坝顶宽8.10 m～8.45 m。大坝表面变形垂直位移观测共设67个测点，其中主坝布置9个断面共19个测点，测点平面布置见图1、主坝典型断面见图2。

图1 垂直位移观测标点分布示意图

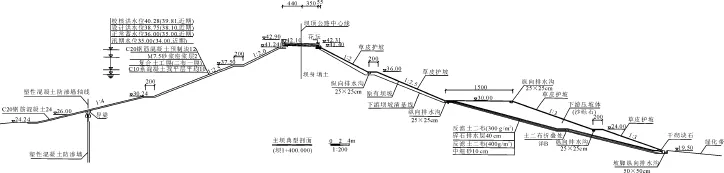
图2 主坝典型横断面图

以LD38测点为例，探讨该土石坝变形特性的非倾向性振荡分析应用。

（1）累计垂直位移变形过程线。根据2005年—2015年表面垂直位移监测资料，主坝最大累计垂直位移量约90 mm，位于测点LD38处，沉降率为0.37%（累计过程线见图3）。

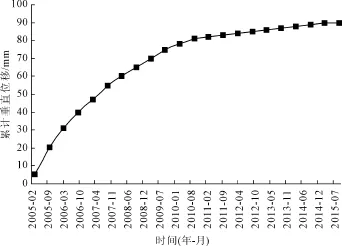
图3 测点LD38累计垂直位移过程线

从图3中可以看出，除险加固后最初几年内，LD38垂直位移较大，沉降速率较快，2010年以后，沉降速率逐渐减小，累计垂直位移趋于稳定。

（2）整体定标指数分析。利用非倾向性振荡分析，拟合该测点2005年—2015年全系列表面变形数据，得出定标指数α=0.96，说明该监测点的垂直位移数据时间序列在各个时间尺度上是正相关或长相关，表明时间序列具有一定的长期记忆性；过去的信息在今后中长期内会继续的影响未来的变化。在未来的时刻里，该监测点的垂直位移仍会呈现出一定的下沉趋势。

（3）年度定标指数变化分析。根据分形理论中非线性振荡分析方法，计算各年的定标指数α（见表1），分析测点LD38表面变形特性。

从表1中可以看出，2005年—2015年各年的定标指数均大于0.5，表明各年内的时间序列具有长期性、持久性的幂律相关，且随着时间推移，变形数据序列的相关性呈现减弱趋势，从2005年开始，定标指数逐年递减，并逐渐趋于0.5。根据定标指数的性质，充分说明测点LD38垂直位移变化表现出较强的随机性，在整体上，该测点的累计垂直位移量较少地受到过去时刻的影响。2010年之后，每年定标指数较为接近，表明该监测点各年份时间序列数据的变化趋势相对一致。

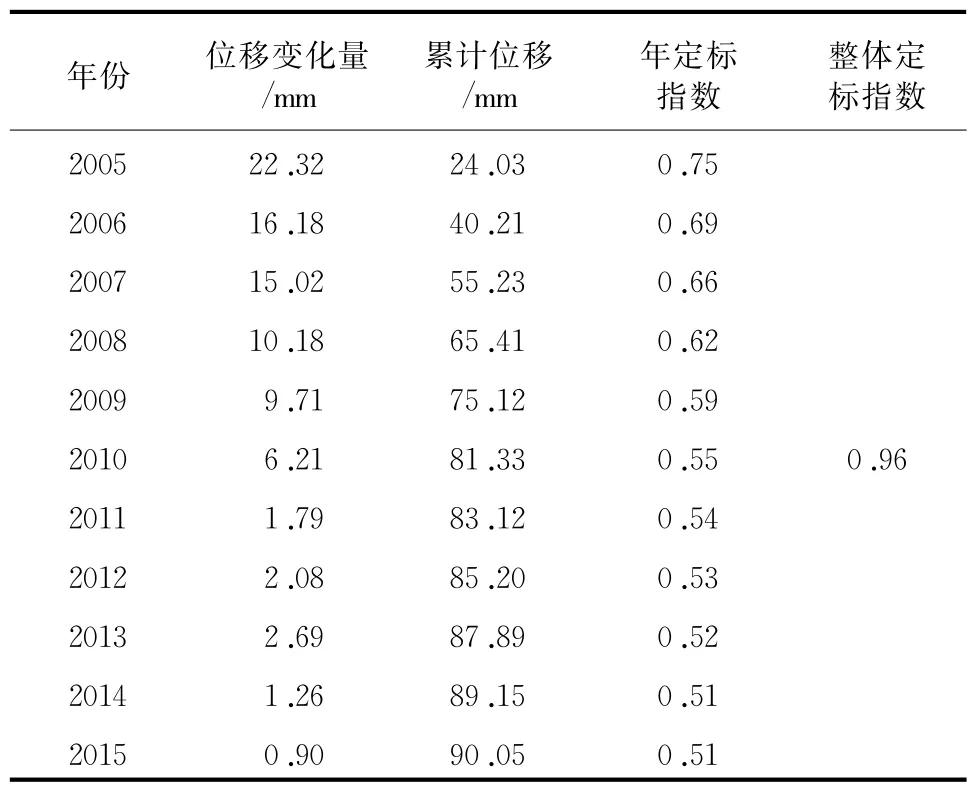
表1 测点LD38位移及定标指数

从工程意义上来讲，该水库除险加固后至2010年，该测点每年表面变形监测数据受施工期和竣工期的影响显著，且长期幂律相关；2010年之后，该测点每年表面变形监测数据受施工期和竣工期的影响较弱，且表现出较强的随机性，表明大坝结构已经趋于稳定。

3 结 语

基于分形学理论的非倾向性振荡分析方法，研究了大坝变形监测数据时间序列的相关性，根据定标指数的取值范围，可判别变形监测数据时间序列是否存在长期相关性，并揭示了动态变化特征；提出的定标指数可用来甄别监测点时间序列的位移值是否存在长期记忆性，有效的预测未来的发展趋势，并指出后续建模选取时间序列的起始范围。

目前非线性振荡分析方法在经济预测、测绘科学、物理学等各个领域中，解决时间序列有关相关性问题上取得很好的结果。将该方法引入到土石坝安全监测变形数据分析，结果表明该方法切实可行。分析结论表明该水库大坝在加固后的5年，大坝沉降变形量较大，受前期影响较为显著，具有长期幂律相关；之后随着时间推移，受前期记忆影响越来越小，变形数据序列的相关性呈现减弱趋势，大坝沉降变形渐趋稳定。

［1］ 张溢丰，朱 华，贾聿颉，等.采空区残余变形预测研究［J］.水利与建筑工程学报，2016，14（2）：90－91.

［2］ 田振华，李传栋，郑东健.R/S分析法在大坝安全监测中的应用［J］.人民黄河，2012，34（2）：106－107.

［3］ 蔡泽宏，简文彬，李宏达，等.基于滑坡监测数据的时间序列位移预［J］.水利与建筑工程学报，2016，14（1）：236－242.

［4］ 王铁生，冯 康，陈正威.深基坑坑周土体水平位移预测模型的研究与改进［J］.水利与建筑工程学报，2015，13（5）：185－187.

［5］ 王中元，周天强，张鹏飞.高层建筑物GPS动态变形监测数据处理［J］.测绘科学，2012，37（1）：47－50.

［6］ 夏 坤，凌 青，高益健，等.盾构法施工地面沉降预测分析研究［J］.水利与建筑工程学报，2015，13（1）：151－157.

［7］ 刘慧荣，周维博，李云排，等.清涧河流域近50年降水变化特征分析［J］.水资源与水工程学报，2013，24（5）：124－130.

［8］ Pu Fangling，Ma Jing，Zeng Dingyang，et al.Early warning of abrupt displacement change at the Yemaomian landslide of the Three Gorge Region［J］.Natural Hazards Review，2015，16（4）：2－8.

［9］ Lee S H，Thomas S R，Tucker R L.Effective practice utilization using performance prediction software［J］.Journal of Construction Engineering&Management，2014，130（4）：576－585.

［10］ Fassman－Beck E，Hunt W，Berghage R，et al.Curve number and runoff coefficients for extensive living roofs［J］. Journal of Hydrologic Engineering，2015，21（3）：221－229.

［11］ Martino G D，Fontana N，Marini G，et al.Variability and trend in seasonal precipitation in the continental United States［J］.Journal of Hydrologic Engineering，2013，18（6）：18－22.

［12］ Wang Zhongsheng，Fan Jun.Fault early recognition and health monitoring on aeroengine rotor system［J］.Journal of Aerospace Engineering，2015，28（2）：213－230.

［13］ Wang Y，Wang S J，Duan X B，et al.Physical modelling of initial seepage failure process［J］.International Journal of Physical Modelling in Geotechnics，2015，15（4）：220－228.

［14］ 王 宇，王士军，谷艳昌.基于分形理论的多孔介质渗透破坏研究［J］.中国农村水利水电，2016（3）：80－87.

［15］ 周志维，段祥宝，谢罗峰，等.土石坝温度观测资料HURST指数研究［J］.中国农村水利水电，2014（6）：182－184.

Detrended Fluctuation Analysis in the Application of Earth－rock Dam Deformation Monitoring Data

CHEN Guoqiang1，WANG Yu2，GU Yanchang2，3，WANG Hong2，3
（1.Yixing City Water Group Co.，Ltd.，Yixing，Jiangsu 214206，China；2.Nanjing Hydraulic Research Institute，Nanjing，Jiangsu 210029，China；3.Dam Safety Management Center of the Ministry of Water Resources，Nanjing，Jiangsu 210029，China）

The traditional time series analysis method adopted to fit the earth and rockfill dam deformation observation data can’t reveal the commonness between deformation observation points.In this paper，fractal theory and detrended fluctuation analysis were combined to analyze time series autocorrelation and the effectiveness to select data continual modeling of earth－rock dam.Then the calibrated index was introduced to describe the dynamic characteristics of deformation data series and forecast the trend of development.Finally，scaling index was proposed to distinguish whether the displacement value of monitoring data sequence“long－term memory”of existence and the future trend of the development of the monitoring points.The proposed method in this paper can provide a better way to analyze earth－rock dam deformation in very complicated state and predict the possible development of survey points in future，which provides a new way to solve various nonlinear problems of earth－rock dam safety analysis in deformation.

earth－rock dam；safety monitoring；deformation；fractal theory；detrended fluctuation analysis

TV641

A

1672—1144（2016）05—0198—04

10.3969/j.issn.1672-1144.2016.05.038

2016－06－04

2016－07－01

水利部公益性行业科研专项（201501033）；土石坝长效安全运行重大关键技术研究；江苏省水利科技项目（2015010）；江苏水库大坝运行管理能力提升研究；南京水利科学研究院中央级公益性科研院所基本科研业务费专项资金项目（Y714004）；基于三维GIS的水库安全监控综合仿真技术研究

陈国强（1969—），男，江苏宜兴人，工程师，主要从事水库大坝安全管理与研究工作。E－mail：18961550928@189.cn

王 宇（1987—），男，江苏泗阳人，博士研究生，研究方向为大坝安全监测与渗流控制。E－mail：wangyu1987710@aliyun.com