预应力锚杆基础非线性抗拔承载力研究

杨 龙，石 炎炎，苑晨阳

（1.中国联合工程公司，浙江杭州310052；2.大连理工大学建设工程学部，辽宁大连116024）

预应力锚杆基础非线性抗拔承载力研究

杨 龙1，石 炎炎2，苑晨阳2

（1.中国联合工程公司，浙江杭州310052；2.大连理工大学建设工程学部，辽宁大连116024）

预应力锚杆基础的抗拔承载力是结构安全的重要保证。以风力发电机预应力锚杆基础为研究对象，通过ABAQUS进行抗拔承载力非线性有限元分析。根据锚杆受力特点，建立包含岩体、砂浆、锚杆和混凝土的单根锚杆有限元模型。研究了三种不同黏聚力和内摩擦角工况下预应力锚杆基础的抗拔承载力；并通过与相同工况下不包含混凝土的模型计算结果对比，得出预应力锚杆基础具有更高的抗拔承载力。

预应力锚杆基础；非线性；ABAQUS有限元分析；抗拔承载力

在能源危机、环境严重恶化的今天，风能作为一种新型能源备受世人重视。风力发电清洁安全，没有环境污染问题，且价格低廉［1-2］。风电机常坐落于采风良好的山坡上，由于地表岩体受风吹日晒、雨水侵蚀等因素的影响，表层岩体材料参数较低。

预应力岩体-锚杆技术作为加固岩体最有效的方法之一，充分利用岩体的抗压强度和锚杆的抗拉性能，与下层材料参数较高的岩体紧密粘结，在相同粘结长度时可提高岩体锚杆基础的极限抗拔承载能力［3-8］。饶枭宇等［9］对预应力岩体锚杆模型内锚段抗拔试验分析，邹志晖等［10］对改变岩体参数和周边约束条件进行模拟试验，赵宇飞等［11］对加预应力锚的节理岩体对比模型试验，马海英等［12］对高耸结构岩体锚杆基础有限元分析，许绍帅等［13］对预应力锚索有限元分析，贾新等［14］采用混凝土模拟岩体材料，对砂浆岩体之间的粘结性能进行研究。

在前人研究基础上［15-19］，本文采用数值模拟方法，对新型风机基础建立有限元模型，对预应力锚杆模型和全粘结锚杆模型进行三维有限元结构分析，研究改变地质条件与荷载工况对结构承载能力的影响。

1 工程概况

拟建风电场位于某山山脊部位，自然山坡稳定，整体上场地无制约工程的滑坡、崩塌等不良物理地质现象，有布置风电场风机的地形条件。混凝土基础直径为11 m，厚1 800 mm，混凝土周边均匀分布28根高强预应力锚杆，锚杆围成的圆直径为10 m，如图1所示；高强预应力锚杆长度为9 500 mm，锚杆顶部套有不易损坏的PE管材，高度为4 150 mm。用混凝土将锚杆和岩体粘结，形成统一整体，在风荷载作用下，锚杆与岩体相互作用承担弯矩荷载。

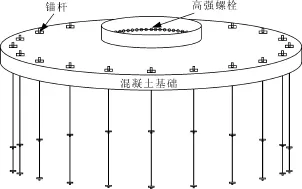
图1 锚杆基础三维视图

2 有限元建模

以锚杆为中心，在整个基础模型上取一半径为1 000 mm圆柱体，建立有限元模型，如图2所示；上部为C40混凝土、Q345锚杆，锚杆外分别为M10砂浆（上）和M50砂浆（下），外部为岩体；混凝土和M10砂浆与锚杆未直接接触（如图3），建模过程中采用不共节点的方法，M10砂浆高2 250 mm；M50砂浆在岩体与锚杆之间起粘结作用，采用共节点的建模方法，M50砂浆高5 200 mm。为分析施加预应力对岩体锚杆基础抗拔承载力的影响，建立如图4所示全粘结锚杆模型，粘结高度为5 200 mm，其他材料参数相同。

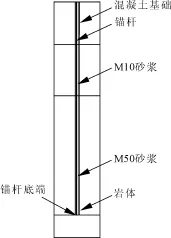
图2 预应力锚杆模型

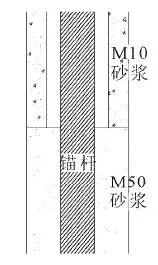
图3 砂浆锚杆粘结详图

图4 全粘结锚杆模型

3 研究目的

岩体锚杆基础中，采用非线性计算方法得到的结果更接近实际破坏状态。锚杆是在岩体自沉降结束后植入岩体内部，然而岩体自重对锚杆的作用可忽略不计［20-23］。

黏聚力和内摩擦角是影响弹塑性材料性质的主要因素，菊存全等［24］通过对岩体特征值的研究发现，由岩体的单向受压原理和摩尔定律可以推导出岩体黏聚力、内摩擦角和岩体极限抗压强度的关系

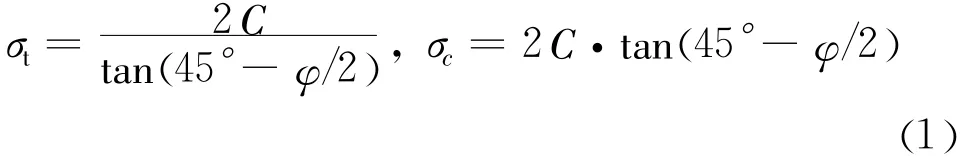
式中：σc、σt为岩体单向抗压强度；C、φ为岩体黏聚力、内摩擦角。根据式（1）可知σt、σc与内摩擦角和黏聚力有关，根据风化程度不同，岩体参数在一定的范围内变化。本文中，岩体采用无质量单元模拟，砂浆、岩体采用D-P模型，锚杆与混凝土采用线弹性模型，讨论改变改变岩体黏聚力、内摩擦角对岩体锚杆基础极限抗拔承载力的影响［25-28］。

4 非线性基础模型抗拔承载力计算

选用预应力锚杆模型（图2）和全粘结锚杆模型（图4），针对3种不同的地质参数，讨论改变地基参数对锚杆极限抗拔承载力的影响和改变基础型式对锚杆抗拔承载力的影响。

在不同工况下，岩体的取值和模型的选择见表1。其中密度设为0是为了不考虑地基重力的影响，在实际情况下，地基已经在重力作用下完成固结，如果密度不为0，在重力计算时地基会因为自身重量下沉，这是与实际不相符的。对于模型中其他材料参数见表2。采用有限元方法对模型整体计算，边界条件是：底部三向约束，周围两向水平约束。观察锚杆顶端位移和模型的屈服区域［29-34］。

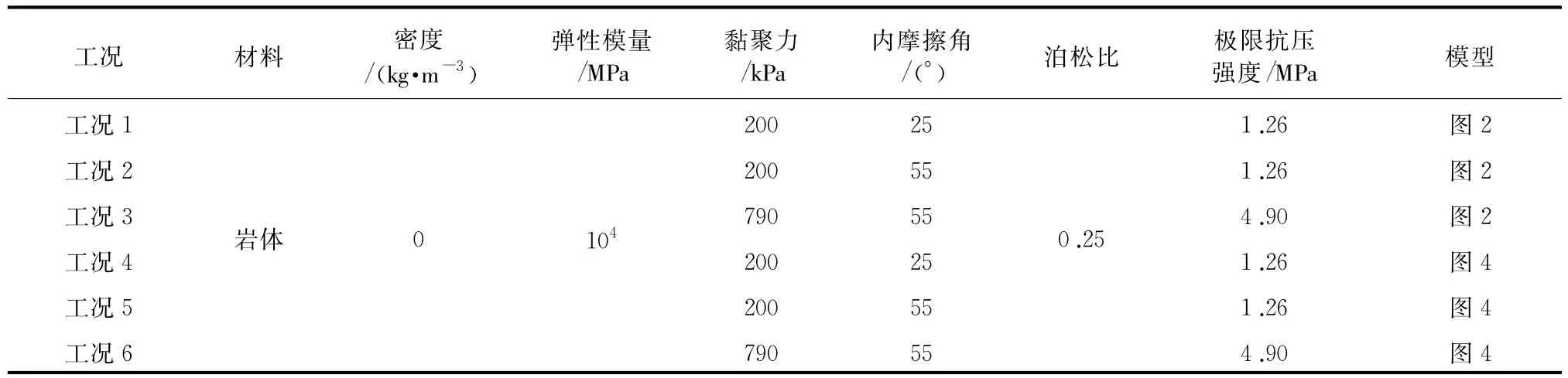
表1 不同工况下地基材料参数取值表

表2 基础材料参数取值表

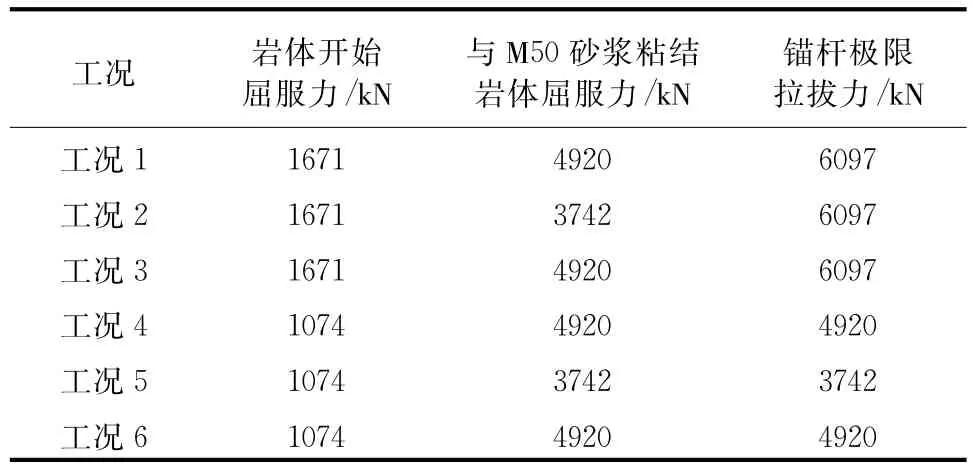
表3 不同工况下基础承载力

工况1：通过对锚杆加载拉拔力计算发现，当锚杆在0～1 671 kN时，模型没有出现屈服现象，整体处于线弹性阶段；当锚杆拉力达到1 671 kN时，M10和M50砂浆接触部位附近的砂浆和岩体开始屈服（图5）；当锚杆拉力达到4 920 kN，与M50粘结的岩体全部屈服（图6），当锚杆拉力达到6 097 kN时，M10砂浆与岩体粘结面屈服，基础模型拉拔破坏（图7）。

图5 1 671 kN 锚杆拉力下塑性应变图

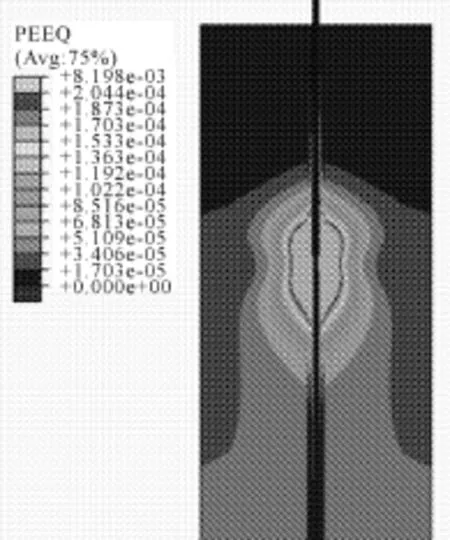
图6 4 920 kN 锚杆拉力下塑性应变图

图7 6 097 kN锚杆拉力下塑性应变图

工况2：当对锚杆的拉拔力在0～1 671 kN之间时，模型没有出现屈服现象，整体处于线弹性阶段，当锚杆拉力达到1 671 kN时，M10和M50砂浆接触部位附近的砂浆和岩体开始屈服（图8）；当锚杆拉力达到3 742 kN时，M10和M50砂浆接触部位附近的砂浆和岩体破坏，M10砂浆与岩体粘结面开始屈服（图9）；当锚杆拉力达到6 097 kN时，M10砂浆与岩体粘结面屈服，基础模型拉拔破坏（图10）。

图8 1 671 kN 锚杆拉力下塑性应变图

图9 3 742 kN 锚杆拉力下塑性应变图

工况3：当对锚杆的拉拔力在0～1 671 kN之间时，模型没有出现屈服现象，整体处于线弹性阶段，当锚杆拉力达到1 671 kN时，M10和M50砂浆接触部位附近的砂浆和岩体开始屈服（图11）当锚杆拉力达到4 920 kN（图12），与M50粘结的岩体全部屈服，当锚杆拉力达到6 097 kN时，M10砂浆与岩体粘结面屈服，基础模型拉拔破坏（图13）。

图11 1 671 kN 锚杆拉力下塑性应变图

图12 4 920 kN 锚杆拉力下塑性应变图

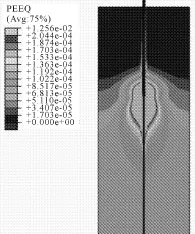
图13 6 097 kN锚杆拉力下塑性应变图

工况4：当对锚杆的拉拔力为1 074 kN时，岩体与M50砂浆接触面略微出现屈服现象（图14），当锚杆拉力达到1 671 kN时，M50砂浆和岩体屈服现象比较明显（图15）；当锚杆拉力达到4 920 kN，与M50粘结的岩体全部屈服，基础模型拉拔破坏（图16）。

图14 1 074 kN 锚杆拉力下塑性应变图

图15 1 671 kN 锚杆拉力下塑性应变图

图16 4 920 kN锚杆拉力下塑性应变图

工况5：当对锚杆的拉拔力为1 074 kN时，岩体与M50砂浆接触面略微出现屈服现象，当锚杆拉力达到1 671 kN时，M50砂浆和岩体屈服现象比较明显（图17）；随着加载值得增加，屈服区域逐渐增大，当加载力达到3 742 kN时，与M50粘结的岩体全部屈服（图18）。

工况6：当对锚杆的拉拔力为1 074 kN时，岩体与M50砂浆接触面略微出现屈服现象，当锚杆拉力达到1 671 kN时，M50砂浆和岩体屈服现象比较明显（图19）。当锚杆拉力达到4 920 kN，与M50粘结的岩体全部屈服，基础模型拉拔破坏（图20）。

图17 1 671 kN 锚杆拉力下塑性应变图

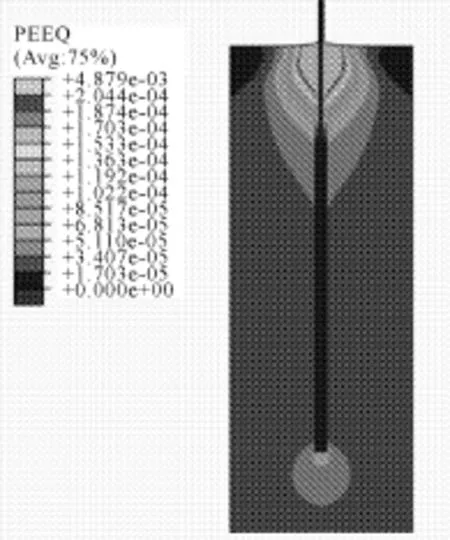
图18 3 742 kN 锚杆拉力下塑性应变图

图19 1 671 kN锚杆拉力下塑性应变图

5 结 论

通过对以上六个工况的有限元分析，得出以下结论：

（1）通过对工况1和工况2的对比分析发现，当其他条件相同时，岩体的摩擦角增大，岩体更容易屈服。

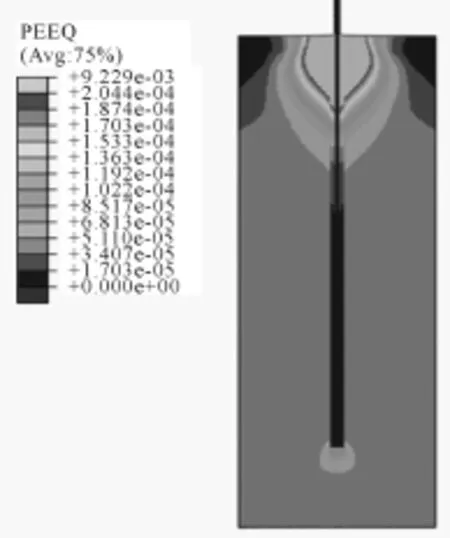
图20 4 920 kN锚杆拉力下塑性应变图

（2）通过对工况2和工况3的对比分析发现，当其他条件相同时，岩体的黏聚力增大，岩体强度更高，更不容易屈服。

（3）通过对工况1与工况4的对比分析发现，采用预应力岩体锚杆基础形式比全粘结岩体锚杆基础形式有更强的极限抗拔能力，更能充分的应用砂浆和地基自身的强度。

（4）通过对表3的数据进行对比可以发现，预应力锚杆模型在岩体开始屈服力和锚杆极限拉拔力上比全粘结锚杆模型大很多，充分证明了预应力锚杆模型具有更高的抗拔承载力。

［1］ 罗承先.世界风力发电现状与前景预测［J］.中外能源，2012，17（3）：24－31.

［2］ 李泓泽，郭 森，王 宝.我国风力发电的环境价值分析［J］.能源技术经济，2011，23（7）：35－39.

［3］ 陈祖煜，杨 健.岩土预应力锚固技术的进展［J］.贵州水力发电，2004，18（5）：5－10.

［4］ 赵明阶，何光春，王多垠.边坡工程处治技术［M］.北京：人民交通出版社，2003：123－125.

［5］ 唐树名.碎裂结构岩体路堑边坡锚固机理分析及其应用研究［D］.重庆：重庆大学，2003：1－9.

［6］ 耿卫红，罗春华.岩土锚固工程技术及其应用［J］.探矿工程，1997（4）：8－10.

［7］ 王 冲.预应力锚固的施工［M］.北京：水利电力出版社，1987.

［8］ 费香泽，程永锋，苏秀成，等.华北地区输电线路岩石锚杆基础试验研究［J］.电力建设，2007，28（1）：26－28.

［9］ 饶枭宇.预应力岩锚内锚固段锚固性能及荷载传递机理研究［D］.重庆：重庆大学，2007.

［10］ 邹志晖，汪志林.锚杆在不同岩体中的工作机理［J］.岩土工程学报，1993，15（6）：71－79.

［11］ 赵宇飞.加锚结构面剪切特性及锚固岩体综合力学模型研究［D］.北京：中国水利水电科学研究院，2013.

［12］ 马海英，谢永健，梁 斌.高耸结构岩石锚杆基础设计及有限元分析马海［J］.河南科技大学学报，2003，24（4）：90－93.

［13］ 许绍帅.有限元数值模拟法研究预应力锚索锚固段应力分布规律［D］.青岛：中国海洋大学，2012.

［14］ 贾新勇，袁 勇，李焯芳.新型玻璃纤维增强塑料砂浆锚杆的黏结性能试验研究［J］.岩石力学与工程学报，2006，25（10）：2109－2114.

［15］ 杨海巍，卢继强，朱少荣.岩锚基础破坏形态与承载力计算的探究［J］.地下空间与工程学报，2009，5（S1）：1306－1311.

［16］ 胡田飞，杜升涛，梁龙龙.微型桩-锚组合抗滑新结构支挡效果的数值分析［J］.防灾减灾工程学报，2015，35（2）：212－218.

［17］ 董建华，朱彦鹏，巍 马.框架预应力锚杆边坡支护结构动力计算方法研究［J］.工程力学，2013，30（5）：250－259.

［18］ 王安明，张淋柄.基坑桩锚支护变形监测与数值模拟研究［J］.水利与建筑工程学报，2015，13（6）：25－30.

［19］ 董建华，朱彦鹏，巍 马.地震作用下框架预应力锚杆边坡锚固结构的动力计算方法［J］.岩石力学与工程学报，2014，33（S1）：3135－3144.

［20］ Graf O，Brenner E.Experiments for investigating the resistance of concrete under often repeated compression loads［C］//Bulletin，Deutscher Aussehuss fur Stahlbeton，Beriin，1934：17－25.

［21］ Raithby K D，Galloway J W.Effects of moisture condition，age，and rate of loading on fatigue of plain concrete［C］// Fatigue of Concrete，SP-4l，American Concrete Institute，Detroit，1974：15－34.

［22］ Petkovic G，Lensehow R，StemlandH，et al.Fatigue of high－strength concrete［C］//American Concrete Institute，Special Publications，SP121－25，1991：505－525.

［23］ Wagaard K.Fatigue of offshore concrete structures－design and experimental nvestigations［C］//OTC Paper 3009.9 Annual Offshore Technology Conference in Huston，1977：341－350.

［24］ 菊存全.岩基承载力特征值的确定研究［J］.科技传播，2014（5）：84－86.

［25］ 余 旭，蔡东阳，陈 东.预应力抗浮锚杆锚固段的参数变化对筏板基础内力影响的研究［J］.安徽建筑工业学院学报，2013，21（1）：9－13.

［26］ 程良奎，张培文，帆 王.岩土锚固工程的若干力学概念问题［J］.岩石力学与工程学报，2015，34（4）：668－682.

［27］ 孙晓云，张 涛，王明明，等.基于改进指-幂混合函数模型的锚杆承载力预测方法研究［J］.岩石力学与工程学报，2015，34（8）：1641－1649.

［28］ 杨校辉，朱彦鹏，黄雪峰.静压桩荷载传递与承载性状试验研究［J］.水利与建筑工程学报，2016，14（1）：139－143.

［29］ 王祥秋，周志国，唐梦雄，等.复杂地层扩体锚抗拔性能研究［J］.公路工程，2013，38（1）：94－98.

［30］ 李振作，张 坤.风机基础用预应力锚杆笼［J］.建设施工，2015（6）：131－135.

［31］ 张 蓓，黄雪峰，宋 楠.深基坑桩锚支护结构锚杆（索）问题分析［J］.四川建筑科学研究，2015，41（1）：168－171.

［32］ 刘泉声，雷广峰，彭星新.深部裂隙岩体锚固机制研究进展与思考［J］.岩石力学与工程学报，2016，35（2）：312－332.

［33］ 周 辉，徐荣超，张传庆，等.预应力锚杆对岩体板裂化的控制机制研究［J］.岩土力学，2015，36（8）：2030－2037.

［34］ 周 勇，朱彦鹏，任永忠.预应力锚杆柔性支护体系中锚杆的变形［J］.中国铁道科学，2015，36（3）：58－65.

Nonlinear Uplift Capacity of Prestressed Anchor Foundation

YANG long1，SHI Yi2，YUAN Chenyang2
（1.China United Engineering Company，Hangzhou，Zhejiang 310052，China；2.Dalian University of Technology，Faculty of Infrastructure Engineering，Dalian，Liaoning 116024，China）

The uplift capacity of the prestressed anchor foundation is an important guarantee for the safety of structure. The prestressed anchor foundation of wind turbine was selected as the research object and the nonlinear finite element analysis was carried out based on the software of ABAQUS to study the uplift capacity.According to the mechanical characteristics of anchors，a single anchor finite element model including rock，mortar，anchor and concrete was established. The uplift capacity of the prestressed anchor foundation was obtained under three scenarios with different values of cohesion and internal friction angle.It is concluded that the prestressed anchor foundation has stronger uplift capacity by comparing other models without considering concrete with the same load scenarios.

prestressed anchor foundation；nonlinear；ABAQUS finite element analysis；uplift capacity

TU472

A

1672—1144（2016）05—0089—06

10.3969/j.issn.1672-1144.2016.05.017

2016－05－30

2016－06－21

杨 龙（1991—），男，河南新乡人，硕士，助理工程师，主要从事项目管理工作。E－mail：1096319943@qq.com