考虑应变软化的T－bar承载力CEL有限元分析

张新全，于 龙，2

（1.大连理工大学水利工程学院，辽宁大连116024；

2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

考虑应变软化的T－bar承载力CEL有限元分析

张新全1，于 龙1，2

（1.大连理工大学水利工程学院，辽宁大连116024；

2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024）

通过欧拉-拉格朗日（Coupled Eulerian-Lagrangian，CEL）大变形有限元对不考虑应变软化的T形触探仪（T－bar）承载力系数进行计算，其计算结果与已有塑性理论解和RITSS（Remeshing and Interpolation with Small Strain，即在小变形有限元的基础上通过网格重剖分和应力插值技术实现大变形有限元分析）的计算结果均吻合较好，验证了CEL计算模型的可靠性。在ABAQUS有限元平台的基础上进行二次开发，编写应变软化子程序计算出考虑应变软化的T－bar承载力系数，其计算结果与RITSS吻合较好，验证了应变软化子程序的可靠性。对T－bar周围土体的软化程度和流动机制分析发现，应变软化使土体抗剪强度减小的同时还改变了土体的流动机制，这两个因素的综合作用导致T－bar的承载力系数减小，从而揭示了应变软化对T－bar承载力系数的影响机理。

耦合的欧拉-拉格朗日大变形有限元；T形触探仪；ABAQUS；应变软化；流动机制

静力触探在现场测试中明确海洋软黏土地基强度特性方面独具优势。经过十几年的发展，触探仪已由传统的锥形发展到触探过程中使土体呈完全流动机制的多种形式：T－bar、盘形和球形触探仪等，如图1所示。相对传统锥形触探仪，全流触探仪存在以下优势：对黏土刚度敏感性低；能通过较少修正情况下准确测出黏土的不排水抗剪强度；承载力系数具有稳定的理论解和数值解。不考虑黏土应变软化的T－bar承载力系数NnosofteningT－bar见式（1）：

式中：qult为T－bar单位投影面积上受土的极限反力；su为黏土的不排水抗剪强度。最初是基于塑性理论解得到的［1］，该方法考虑圆柱探头表面的粗糙程度算出的范围为9.1（完全光滑）～11.9（完全粗糙）。一般取=10.5来分析T－bar测试结果［2］。

众多学者对T－bar触探试验的承载力系数进行了研究。Randolph M F等［3］、Martin C M等［4］根据极限分析方法得到了T－bar承载力系数的塑性理论解。范庆来等［5］通过ABAQUS有限元分析了应变软化对T－bar承载力系数的影响，但由于T－bar位移行程不够，未得到考虑应变软化的T－bar承载力系数。郭绍曾［6］用CEL方法模拟了T－bar在无软化无摩擦无重度黏土中的贯入，得到的T－bar承载力系数比较离散。周琪等［7］采用FLAC3D研究了应变软化对水平埋置条形锚板承载力的影响。张辉等［8］采用PFC2D研究了砂土中埋设T－bar的竖向抗拔特性。Low W E等［9］分析3个陆上工程和7个海上工程勘察资料，发现液性指数和塑性指数对全流贯入仪贯入阻力有一定影响。

图1 触探仪

实际情况下T－bar贯入时，周围土体要经历较大的变形从而发生应变软化，这对于高敏感度土体的T－bar承载力系数造成显著的影响。若想利用T－bar触探仪精准地确定黏土的抗剪强度，必须对考虑应变软化的T－bar承载力系数进行充分的研究。Zhou H等［10］在T－bar和球形触探仪数值计算与理论分析的基础上，提出了考虑应变软化效应的土体抗剪强度计算模型，见式（2）：

式中：FV1代表应变软化效应，其中各参数的物理意义为：su0是土体没有扰动的初始抗剪强度；δrem是完全扰动后的土体抗剪强度与su0的比值（即为敏感度ST的倒数）；ξ是土体单元的累积绝对塑性剪应变；ξ95是土体单元受到95%扰动所需的ξ值，此值反应土的塑性和软化快慢，典型的取值为10～50［11］。Zhou H等［10］采用式（2）所示软化模型利用大变形有限元方法（RITSS）对T－bar贯入过程进行了数值分析，考虑了不同组合的软化参数δrem和ξ95对 T－bar承载力系数的影响，给出了与δrem和ξ95的关系见式（3）：

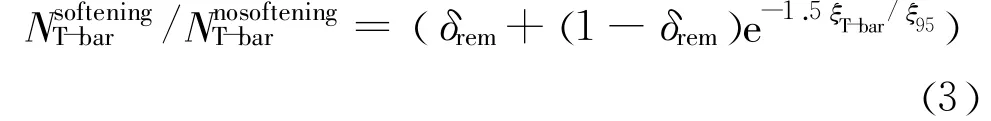
本文在ABAQUS程序CEL算法中通过用户子程序实现了公式（2）的应变软化模型，对T－bar贯入均质黏土过程进行了分析，细致讨论了应变软化参数ξ95对土体软化程度和流动机制的影响，揭示了理论分析和大变形有限元拟合所得ξT－bar数值不同的原因和应变软化对T－bar承载力系数的影响机理。

1 CEL方法简介

在拉格朗日有限元中，连续体的变形被定义为物质点坐标与时间的函数，单元结点位置随着物质运动而发生变化，这种单元形式的优点在于能够准确描述系统中不同介质之间的接触界面，但在大变形过程中将遇到网格严重扭曲而导致计算中断的问题。而欧拉单元则把连续体的运动表达为空间坐标与时间的函数，在分析过程中，欧拉网格不发生变形，而物质可以在欧拉网格内运动，因此欧拉单元不会产生网格扭曲，可以有效解决大变形问题中网格畸形带来的弊端。CEL有限元方法是在综合拉格朗日单元和欧拉单元优点的基础上发展起来的。拉格朗日网格内的物质与欧拉网格内物质之间的界面通过广义接触算法来模拟，虽然不如动态接触方法严格，但是可以保证在困难情况下算法的收敛。CEL有限元采用基于中心差分准则的显式动力学解法来求解非线性微分方程体系，该算法中稳定时间增量步长在计算过程中自动获取，因而其分析过程相对其他大变形有限元比较简单。

2 T－bar贯入CEL有限元模型

由于对称性，黏土地基模型和T－bar模型只取一半，如图2所示。T－bar和黏土地基模型均采用八节点方块单元，黏土地基模型采用欧拉单元模拟，T－bar模型采用拉格朗日单元模拟，在土体表面线上方设置一层厚度为1D（D为T－bar直径）的空欧拉单元以适应T－bar贯入过程中土体表面的隆起。整个模型厚度方向只取一个网格，模拟平面应变问题。地基模型为均质黏土，采用摩尔库伦屈服准则，黏土的硬度su0/γD取0.5，其中γ为土体重度（硬度为控制T－bar临界埋深率的指标［13］，临界埋深率即T－bar刚好达到全流破坏机制时对应的埋深率，此时T－bar承载力达到极限值）。土体弹性模量和泊松比分别取为E=500su0和ν=0.495。T－bar被模拟为刚体，T－bar与土体之间为通用接触，采用粘滞摩擦系数α模拟T－bar与土体之间的摩擦，即接触面的切应力τ=αsu0，在软化计算中α取为ST的倒数，T－bar由黏土表面向下贯入4D。首先计算T－bar在无软化黏土中的承载力系数，之后在ABAQUS平台上进行二次开发，通过FORTRAN语言将式（2）所示应变软化模型写入用户子程序，用应变软化效应函数FV1控制土体的软化程度，保持α=δrem=0.2不变，取不同的ξ95值计算考虑应变软化的T－bar承载力系数。

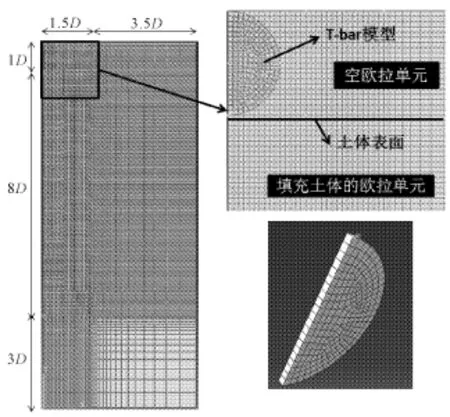
图2 T－bar贯入CEL有限元计算模型

正常情况下T－bar的贯入过程是准静态的，在CEL中是用动态显示算法代替准静态加载，为了在节省计算时间的基础上让动态显示算法逼近静态隐式进行欧拉分析之前需要对拉格朗日体的加载速度和欧拉体的网格尺寸分别做速度收敛性分析和网格收敛性分析［14］。本文做了速度收敛性分析来研究拔出贯入速度v对计算结果的影响：先将最小网格尺寸设定为h=D/20，选取三个贯入速度为v=0.2 D/s、0.1D/s和v=0.05D/s进行计算，得到T－bar的抗力位移曲线见图3。计算结果表明，贯入速度越大，T－bar承载力系数稍微变大，v=0.1D/s和v= 0.05D/s对应的荷载位移曲线相当接近，本文接下来的计算都采取了v=0.1D/s的贯入速度，可以认为是准静态加载。本文网格收敛性分析结果如图4所示。将贯入速度设为v=0.1D/s，选取三个不同的最小网格尺寸h=D/10、D/20和D/40进行计算。计算结果表明，h=D/20的网格尺寸足够精细，接下来的计算最小网格尺寸都取h=D/20。

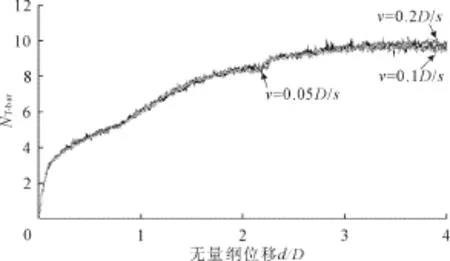
图3 速度收敛性分析

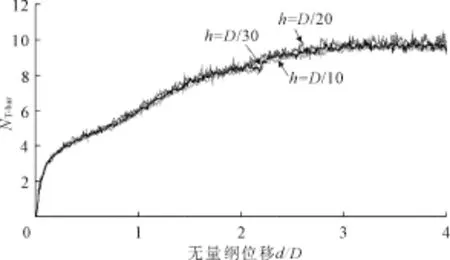
图4 网格收敛性分析

3 T－bar贯入抗力-位移计算结果

首先分析不考虑应变软化情况下T－bar贯入过程，其抗力-位移曲线如图5所示与 RITSS方法［10］和塑性理论解［10］的计算结果比对见表1。α=0时，本文CEL得到的比下限塑性解小3.5%，比上限塑性解小4.0%。α=0.2时，本文CEL得到的比下限塑性解小3.0%，比上限塑性解小3.2%，比RITSS方法小3.5%。 α=1时，本文CEL得到的比上、下限塑性解小3.6%，比RITSS方法小4%。计算结果表明，不管是否考虑摩擦，本文CEL方法计算出的无软化T－bar承载力系数与RITSS方法和上、下限塑性解吻合较好，说明了本文CEL模型的可靠性。

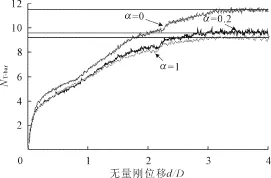
图5 不考虑应变软化的T－bar抗力-位移曲线

表1 NnTo－sboafrtening不同方法的计算结果

其次，分析考虑应变软化情况下的T－bar贯入过程。在计算时，摩擦和应变软化参数的设定与Zhou H等［10］一致，即α=δrem=0.2不变，ξ95分别取10、15、25和50，共4组工况。本文CEL方法得到的考虑应变软化的T－bar抗力-位移曲线见图6，得到的与Zhou H等［10］和公式（3）的结果（ξT－bar取3.7）对比见表2。ξ95=10时，本文CEL得到比RITSS方法计算结果大0.5%，比式（3）的结果大1.1%。ξ95=15时，本文CEL得到比RITSS方法计算结果小3.8%，比式（3）的结果小4.4%。ξ95=25时，本文CEL得到比RITSS方法计算结果小8.6%，比式（3）的结果小7.0%。 ξ95=50时，本文CEL得到比RITSS方小8.8%，比式（3）的结果小6.7%。考虑应变软化的计算结果表明，本文CEL方法通过应变软化子程序计算出的与Zhou H等的RITSS方法计算结果吻合较好，充分验证了本文应变软化子程序的正确性，同样与式（3）ξT－bar取3.7时的结果吻合较好，说明本文CEL计算结果拟合出的ξT－bar也为3.7。

4 土体的软化程度和流动机制分析

首先，分析ξ95对T－bar周围土体软化程度的影响。ξ95=10、ξ95=25和ξ95=50三种工况土体软化程度见图7，由图7可知：图7（a）对于ξ95=10、ξ95= 25和ξ95=50，T－bar上方均存在一定区域的土体已经完全软化（即su/su0=0.2=δrem所代表的区域），ξ95越小，完全软化区越大，这是因为ξ95越小，土体在较小应变情况下就发生了完全软化；图7（b）由T－bar的右侧边缘到土扰动区边缘，su/su0由0.2过渡到1，且ξ95越小，扰动区的宽度越小，抗剪强度的分布越不均匀；图7（c）对于不同ξ95取值情况下，T－bar正下方土的软化程度差异不大，这是因为这部分土体累积剪应变相对较小。

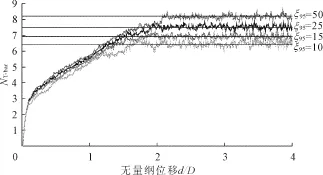
图6 考虑应变软化的T－bar抗力-位移曲线（α=δrem=0.2）

表2 NsTo－fbte anring不同方法的计算结果

其次，分析ξ95对T－bar周围土体流动机制的影响。土体流动机制矢量图见图8，由图8可知：图8（a）α=0.2无软化对应土体流动机制为旋转破坏模式，与Martin C M等［15］、Einav I等［12］在上限极限分析中所假设的位移破坏模式吻合。图8（b）ξ95不同，对应的流动机制形状和大小均发生了变化，ξ95越小，流动机制范围越小。这是因为ξ95越小，土体软化越快而抗剪强度分布越不均匀，土体总是沿着最容易的方向流动。Einav I等［12］中的理论分析是建立在相同流动机制基础上（假定考虑软化流动机制同不考虑软化情况相同），仅变化剪切带上的土体抗剪强度，得出ξT－bar=3.85；而本文和Zhou H等［10］的大变形计算结果都表明ξT－bar=3.7，理论分析和大变形有限元分析所得结果有所区别的原因就在于大变形有限元分析考虑了应变软化对流动机制形状和大小的实时影响。

图7 土体软化程度云图

图8 T－bar周围土体流动机制矢量图

5 结 论

本文通过编写用户子程序在CEL算法中实现了考虑土体的应变软化特性，并对T－bar贯入过程进行了模拟，揭示了应变软化对T－bar承载力系数的影响机理。主要结论为：

（1）通过对CEL中T－bar贯入模型的速度和网格分析，本文建议使用h=D/20的最小网格尺寸和v=0.1D/s贯入速度。

（2）无软化计算结果与已有文献塑性理论解和RITSS分析结果吻合较好。考虑应变软化的计算结果与已有文献RITSS方法计算结果吻合较好，验证了本文计算模型和应变软化子程序的正确性。

（3）考虑应变软化时，T－bar周围土体抗剪强度不均匀，导致T－bar流动机制形状和大小发生改变。流动机制的改变和土体强度的弱化综合作用导致T－bar承载力系数减小。

［1］ Randolph M F，Martin C M，Hu Y.Limiting resistance of a spherical penetrometer in cohesive material［J］.Geotechnique，2000，50（5）：573－582.

［2］ Randolph M F，Hefer P A，Geise J M，et al.Improved Seabed Strenght Profiling Using T-Bar Penetrometer［C］// Offshore Site Investigation and Foundation Behaviour’New Frontiers：Proceedings of an International Conference.Society of Underwater Technology，1998.

［3］ Randolph M F，Houlsby G T.Limiting pressure on acircular pile loaded laterally in cohesive soil［J］.Géotechnique，1984，34（4）：613－623.

［4］ Martin C M，Randolph M F.Upper－bound analysis of lateral pile capacity in cohesive soi1［J］.Géotechnique，2006，56（2）：141－146.

［5］ 范庆来，栾茂田，刘占阁.软土中T型触探仪贯入阻力的数值模拟［J］.岩土力学，2009，30（9）：2850－2854.

［6］ 郭绍曾.静力触探测试技术在海洋工程中的应用［J］.岩土工程学报，37（S1）：207－211.

［7］ 周 琪，于 龙.考虑黏土应变软化的锚板承载力数值分析［J］.水利与建筑工程学报，2014，12（4）：124－128.

［8］ 张 辉，于 龙，王 博，等.砂土中埋设管线竖向抗拔特性研究［J］.水利与建筑工程学报，2015，13（5）：156－160.

［9］ Low H E，RandolphM F，Lunne T，et al.Effect of soil characteristics on relative values of piezocone，T－bar and ball penetration resistances［J］.Géotechnique，2011，61（8）：651－664.

［10］ Zhou H，Randolph M F.Resistance of full－flow penetrometers in rate－dependentand strain－softeningclay［J］. Géotechnique，2009，59（2）：79－86.

［11］ Chung S F，Randolph M F.Penetration resistance in soft clay for different shaped penetrometers［C］//Proc.2nd Int. Conf.on Site Characterisation，Porto.2004，1：671－678.

［12］ Einav I，Randolph M F.Combining upper bound and strain path methods for evaluating penetration resistance［J］.International Journal for Numerical Methods in Engineering，2005，63（14）：1991－2016.

［13］ White D J，Gaudin C，Boylan N，et al.Interpretation of T－ bar penetrometer tests at shallow embedment and in very soft soils［J］.Canadian Geotechnical Journal，2010，47（2）：218－229.

［14］ Chen Z，Tho K K，Leung C F，et al.Influence of overburden pressure and soil rigidity on uplift behavior of square plate anchor in uniform clay［J］.Computers and Geotechnics，2013，52（7）：71－81.

［15］ Martin C M，RandolphM F.Upper bound analysis of lateral pile capacity in cohesive soil［J］.Geotechnique，2006，56（2）：141－145.

CEL Finite Element Analysis of T－bar Bearing Capacity with Strain Softening

ZHANG Xinquan1，YU long1，2
（1.School of Hydraulic Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China；2.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

The T－bar bearing capacity coefficients without considering strain softening was calculated by CEL（Coupled Eulerian-Lagrangian），a large deformation finite element method.The results from CEL method are in good agreement with the results of existing plastic theoretical solutions and RITSS（remeshing and interpolation with small strain，in which the large deformation finite element analysis is realized by remeshing technique and stress interpolation technique on the basis of small deformation finite element），thus the reliability of the CEL calculation model is verified.Based on the ABAQUS finite element platform，we developed a new compile strain softening subroutine to calculate T－bar bearing capacity coefficient considering strain softening.The results by strain softening subroutine are in good agreement with the results of RITSS，so the reliability of the strain softening subroutine is verified.By analyzing the degree of softening and flow mechanism of soil around T－bar，it can be found that strain softening not only reduces the shear strength of soil，but also changes its flow mechanism.The combined effects of these two factors lead to the decrease of the bearing capacity coefficient of T－bar.So，the effect mechanism of strain softening on the bearing capacity coefficient of T－bar was revealed.

CEL large deformation finite element；T－bar；ABAQUS；strain softening；flow mechanism

TU447

A

1672—1144（2016）05—0050—05

10.3969/j.issn.1672-1144.2016.05.010

2016－05－16

2016－06－14

国家自然科学基金项目（51539008，51479027）；中央高校基本科研业务费专项资金项目（DUT15LK36）

张新全（1991—），男，湖北荆州人，硕士研究生，研究方向为大变形有限元分析。E－mail：zhangxinquan7919@163.com

于 龙（1979—），男，辽宁辽阳人，博士，副教授，主要从事海洋基础承载力和大变形有限元分析方面的工作。E－mail：longyu@dlut.edu.cn