源于课本回归本质——对一道高考题的解法探究与拓展延伸
2016-11-19浙江省诸暨市湄池中学蔡旦燕
☉浙江省诸暨市湄池中学 蔡旦燕
源于课本回归本质——对一道高考题的解法探究与拓展延伸
☉浙江省诸暨市湄池中学蔡旦燕
2016年高考已经落下帷幕,作为传统高考的最后一年,社会各界对浙江省高考的关注度前所未有.2016年浙江高考数学试题,笔者总体感受是“题型稳、入口宽、坡度缓、立意精准、稳中有新、关注思维、凸显能力”.在知识点考查、试题结构、材料选取、语言表述、命题立意、思想内涵等方面都呈现了这些特点.
一、题目呈现
设数列{an}满足
(1)证明:|an|≥2n-1(|a1|-2),n∈N*;
二、试题简评
本试题言简意赅,朴实无华,解法灵活,显现能力.题目两个小问,呈现平和自然,表述精炼清晰,文字量少,阅读量小,有亲切感,易于激发学生解决问题的冲动.作为一道压轴题,以数列为载体,主要考查数列的递推关系与单调性、不等式性质等基础知识,同时考查推理论证能力、分析问题和解决问题的能力.试题设计立意鲜明,角度宽,视点多,深入考查了数学理性思维.深化能力立意是数学命题一直以来的追寻目标,本试题真正地体现了“以能力立意为指导,以考查能力和素质”的命题原则.
三、解法探究

(2)任取n∈N*,由(1)知,对于任意m>n,都有的任意性可得|an|≤2.

点评:此解法是由绝对值三角不等式入手,结合数列方法解决.该法起步低,坡度缓,比较容易想到.本题也可将有理式递推关系变为整式递推关系
(2)任取n∈N*,由(1)知,对于任意m>n,|am|≥2m-n·(|an|-2),即
点评:此法利用待定系数或配凑得出类递推公式|an+1|-2≥2(|an|-2),注意此处不能写为累乘,因为符号未知,不等号方向可能会发生变化,而是要用递推关系不断迭代得出结果.第(2)小题的证明则是利用第(1)小题的结论顺势证明,比较自然.

(2)同证法2.
点评:此法看似与证法2类似,其实本质上有很大区别,递推过程需要不断迭代,尤其要注意在递推关系给出后,要将后面等比数列累加求和.

(2)假设|an|>2,由(1)知,对于任意(|an|-2),对任意正整数n,右侧为确定的正数,记为f(n),取m=,则有m>0,而当p→+∞时也就是一定会存在一个p使得2),与题设矛盾,故|an|>2不成立,即|an|≤2.
点评:此法用绝对值三角不等式的顺序与前几种方法有所不同,但结果一样.在第(2)小题采用了反证法,更符合学生思维习惯.
四、背景探究
本题秉承了浙江省数学高考题的一贯特点:叙述简洁、概念清晰、思维深刻、解法多样等.“入手容易深入难”,由“知识立意”深化至“能力立意”,意蕴深邃,平淡之中显新意.在初看此题时是一个数列的上下界估计的问题.此题的背景是人教A版教材必修1第95页第三章《函数模型及其应用》例1——投资收益模型(图1).
例1假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天以前一天多回报10元;
方案三:第一天回报0.1元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
分析:我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据.
函数图像是分析问题的好帮手,为了便于观察,我们用虚线连接离散的点.
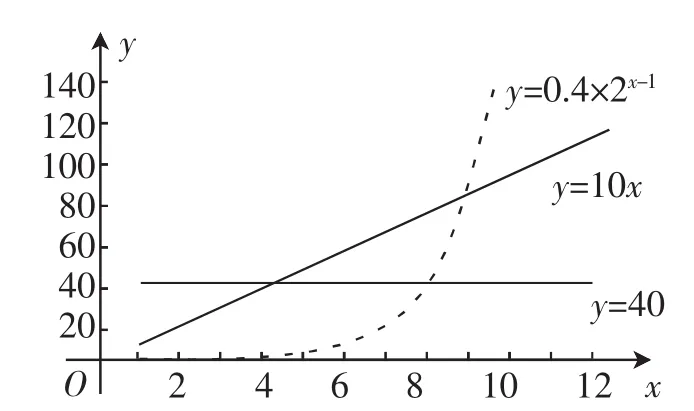
图1
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多,从中你对“指数爆炸”的含义有什么新的理解?
根据试题命制双向细目表,第20题要考查的核心知识是数列、函数、不等式,考查题目的能力立意是推理论证能力、分析问题和解决问题的能力.命题组专家在编制此题时,选择把目光投向教材,巧妙地选取了人教A版教材必修1第95页第三章《函数模型及其应用》例1中的方案三:翻倍回报即指数函数模型,在保持数学思想的基础上进行创新拔高.设前一年的回报为an,后一年的回报为an+1,若an+1是an的两倍,那么2an-an+1=0.但是在现实生活中,常常存在一定的误差,将误差范围控制在2以内,得到,以此作为题干条件.第(1)小题的问题|an|≥2n-1(|a1|-2),其实是最终回报不低于2n-1|a1|-2n,即数列的下界.
第(2)小题中,如果不加条件,最终回报很有可能指数爆炸无限上升,所以加了一个限制条件,就使得最终回报也就是an最大值不超过2,即数列的上界.
这道压轴题兼具函数和数列思想,具有科学性和生活气息,使人回味无穷,是一道不可多得的好题.众所周知,第20题作为整张试卷的压轴题,起到了选拔优秀的、有潜力学生的功能,会有一定难度,但是一旦看破此题的背景与本质,这样的难度也是非常自然的.
五、推广延伸
基于上面的分析,此题可以作以下推广和延伸:
推广1:设数列{an}满足
(1)求证:|an|≥2n-1(|a1|-4),n∈N*;
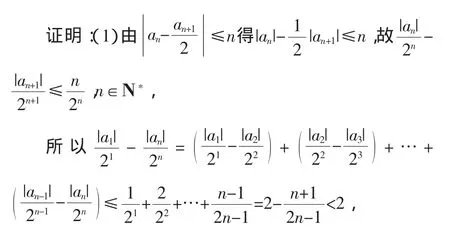
因此|an|≥2n-1(|a1|-4).
(2)任取n∈N*,由(1)知,对于任意m>n,
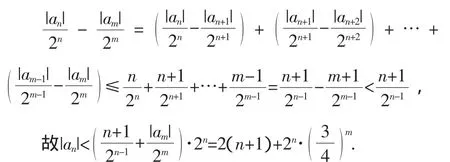
由m的任意性得|an|≤2(n+1).
推广2:设数列{an}满足
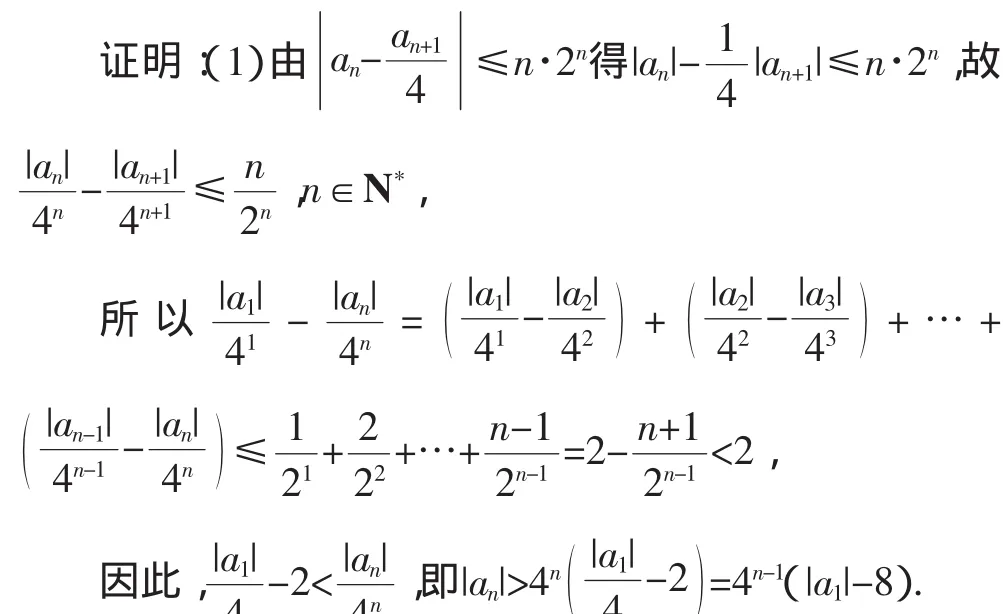
(2)任取n∈N*,由(1)知,对于任意m>n,
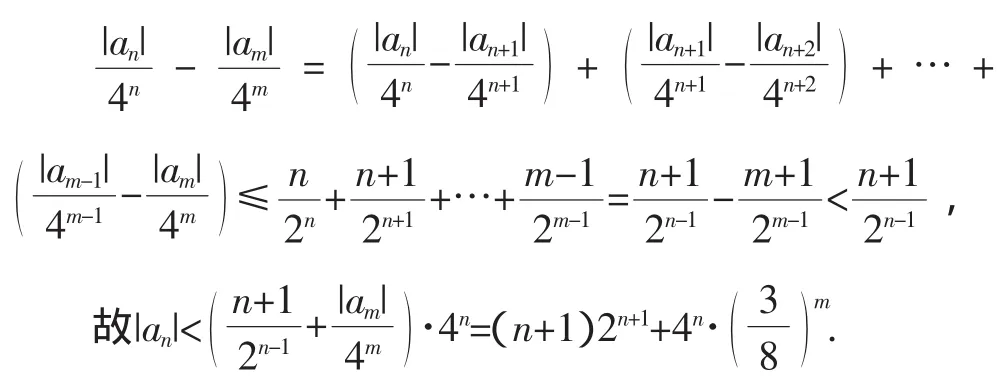
从而对于任意m>n,均有|an|<(n+1)2n+1+4n·
由m的任意性得|an|≤(n+1)2n+1.
六、结束语
2016年浙江高考数学理科第20题解法探究、背景分析及拓展推广,为我们平时的教学提供了有益的启示:一是要立足课本,突出数学思想地位,盲目的题海战术,已适应不了当前的高考.教学要回归教材,但是回归教材不是喊口号,高考题不可能出现与课本题一模一样,甚至形式一样都很少,但是思想一定是一脉相承,此题启发我们在回归课本,研究课本时,不能浮于表面,而要立足教材,活于教材、高于教材.二是要注重渗透,提升数学核心素养.抓好学生的基础知识、基本技能,平时教学中要注重反思、重视思维的渗透,善于揭示数学思想的本质,在培养学生的思维能力,提升我们的学生数学核心素养上做功课.
