哈拉哈塘碳酸盐岩油藏数值试井研究

程汉列 王连山 王建民 刘 勇 朱 轶 张 磊

(1. 西安石油大学地球科学与工程学院， 西安 710065；2. 恒泰艾普石油天然气技术服务股份有限公司， 新疆 库尔勒 841000；3. 中国石油塔里木油田分公司开发事业部， 新疆 库尔勒 841000)



哈拉哈塘碳酸盐岩油藏数值试井研究

程汉列1,2王连山2王建民1刘 勇3朱 轶3张 磊2

(1. 西安石油大学地球科学与工程学院， 西安 710065；2. 恒泰艾普石油天然气技术服务股份有限公司， 新疆 库尔勒 841000；3. 中国石油塔里木油田分公司开发事业部， 新疆 库尔勒 841000)

讨论了缝洞型碳酸盐岩油藏试井解释的复杂性及常规试井解释的局限性。针对哈拉哈塘碳酸盐岩油藏的地质特征，利用数值试井技术，结合油藏地质特征，构建有限元数值试井模型进行拟合分析，得到油藏不同区域储层的渗流特征、储量情况及油藏边界范围。并针对该区块常见的多缝洞体井控面积大和定容井控面积小2种油藏类型，提出了相应的增产措施。应用实例表明，数值试井技术能有效描述油藏的真实情况，为后期开发措施的制定提供理论依据。

缝洞型油藏； 数值试井； 渗流特征； 增产措施

随着试井理论和应用技术的发展，均质油藏解析试井理论已比较成熟和完善，解释结果与实际情况符合程度高。但对于复杂缝洞型碳酸盐岩油藏试井分析，采用解析试井方法解释的结果不理想[1]。由于解析试井的解释模型有限，往往所选解释模型不能真实反映实际油藏的地质特征，因此难以准确描述油藏生产动态。

近年来随着计算机技术及硬件的飞速发展，数值试井利用网格剖分技术，采用数值方法求解复杂试井数学模型，建立离散数值模型，输入产量后能同时输出压力与实测压力；能建立任意角度、形状及不同类型的多种外边界组合；通过不断调整、改善数值模型结构、形状和相关参数来精确描述油气藏外部边界形态[2-3]。

数值试井方法理论上已取得了良好的应用成果[4]，但在复杂缝洞型碳酸盐岩试井评价及利用评价结果指导后期增产措施方面，仍需要进一步研究。利用KAPPA公司的Saphir软件，对塔里木盆地哈拉哈塘油田2口典型缝洞型碳酸盐岩油藏进行数值试井研究。结果表明，针对复杂的油藏地质特征，利用数值试井进行研究分析，能更准确地进行描述，解释的结果更符合油藏真实的地质情况，可为后期制定增产措施提供理论依据。

1 缝洞型碳酸盐岩试井解释复杂性分析

缝洞型碳酸盐岩多样的储集类型、储集体组合关系及强非均质性，不仅对常规试井解释方法提出了挑战，也对特殊试井方法提出了新要求[5]。常规试井解释的核心在于油藏模型的合理选择，油藏模型选择正确与否，决定了对储渗机理、发育规模、渗流边界等油藏特征描述的准确性。常规解释方法中理论模型是固定的，难以满足复杂缝洞型碳酸盐岩油藏试井分析的需要。缝洞型碳酸盐岩试井解释的复杂性主要体现在解释模型、静态参数误差和探测半径分析3个方面。

1.1 解释模型

试井解释是一个求解反问题的过程，解释模型为一个转化函数，用来描述井和油藏动态特征，不是生产系统的真实属性[3]，其解往往并不唯一，对于同一套压力响应数据，可找到多个合适的解释模型。模型校正和有效性检验需通过地质、地球物理、油层物理和流体描述特征来实现。

1.2 静态参数误差

静态参数误差直接影响解释结果，但并不影响试井模型选择。当已知静态参数不准时，通常采用近似值进行初步分析，然后通过参数对解释结果进行校正。如缝洞型碳酸盐岩几乎无法准确确定油层净厚度h。另外，若原油黏度μ由关系式推导得出，那么流体特征关系式可靠性就较低。但试井解释只提供了流动系数Khμ，因此，h或μ的任何误差都会影响渗透率K的估算。探测半径ri及井离边界的距离都与h有关，但与μ无关。总压缩系数Ct是各相饱和度的函数，该参数取值较难估计，在均质无限作用油藏中，该值只对表皮系数S和距离产生影响[13]。经推导，若Ct是实际值的10倍，则计算的探测半径是实际值的3.16倍，计算的表皮系数是实际值的1.15倍，误差较大。

1.3 探测半径

探测半径ri作为储量分析中的重要参数，通常测试过程中观察不到压力相应的径向最小距离，其仅是数学概念的近似值。早期不稳定半径大于试井方法估算的探测半径。受解释所得参数平均化的影响，压力响应并不代表生产井所影响的整个油藏区域，实际上仅反映井筒附近的环形区域。

故分析中考虑采用参数团来分析油藏渗流特征，并与地质、物探资料结合使试井解释结果符合油藏地质特征。

2 实例应用分析

通过对哈拉哈塘油田试井特征分析评价[6-8]，按照不同缝洞组合关系及实际油藏地质特征，选择2类典型井：(1)多缝洞型，以YUEMa井为例；(2)定容型，以YUEMb井为例。利用数值试井解释精细描述油藏特征。

2.1 多缝洞型应用分析

YUEMa井位于层间岩溶断裂改造区。在三维地震叠前深度偏移剖面上，一间房组顶面附近表现为“串珠”及“杂乱”地震响应特征。天然缝洞系统发育情况受断裂交汇控制，该大型缝洞集合体主要由“串珠”群构成，平面上呈近南 — 北向条带状展布，面积1.76 km2，井点位于大型缝洞体储层发育高部位。钻至井深7 279 m时发生溢流(溢流量为 0.5 m3)，关井，观察套压。套压由0 MPa上升到 27 MPa，因此说明用相对密度为1.8的压井液压井成功。随后下钻出现遇阻、出口失返现象，故提前完钻，三开累计漏失钻井液43.8 m3。因井下情况复杂未进行测井。

投产前进行压力恢复测试，双对数曲线反映储层具有内好外差的复合型特征，解析试井选择井储+表皮+径向复合储层+矩形边界模型，拟合分析得到：内区地层流动系数11.758 μm2·mmPa·s、地层系数9.31 μm2·m、渗透率1.591 μm2、复合半径264 m、外区渗透率0.023 μm2，3条边界的距离分别为434、530、324 m(图1)。

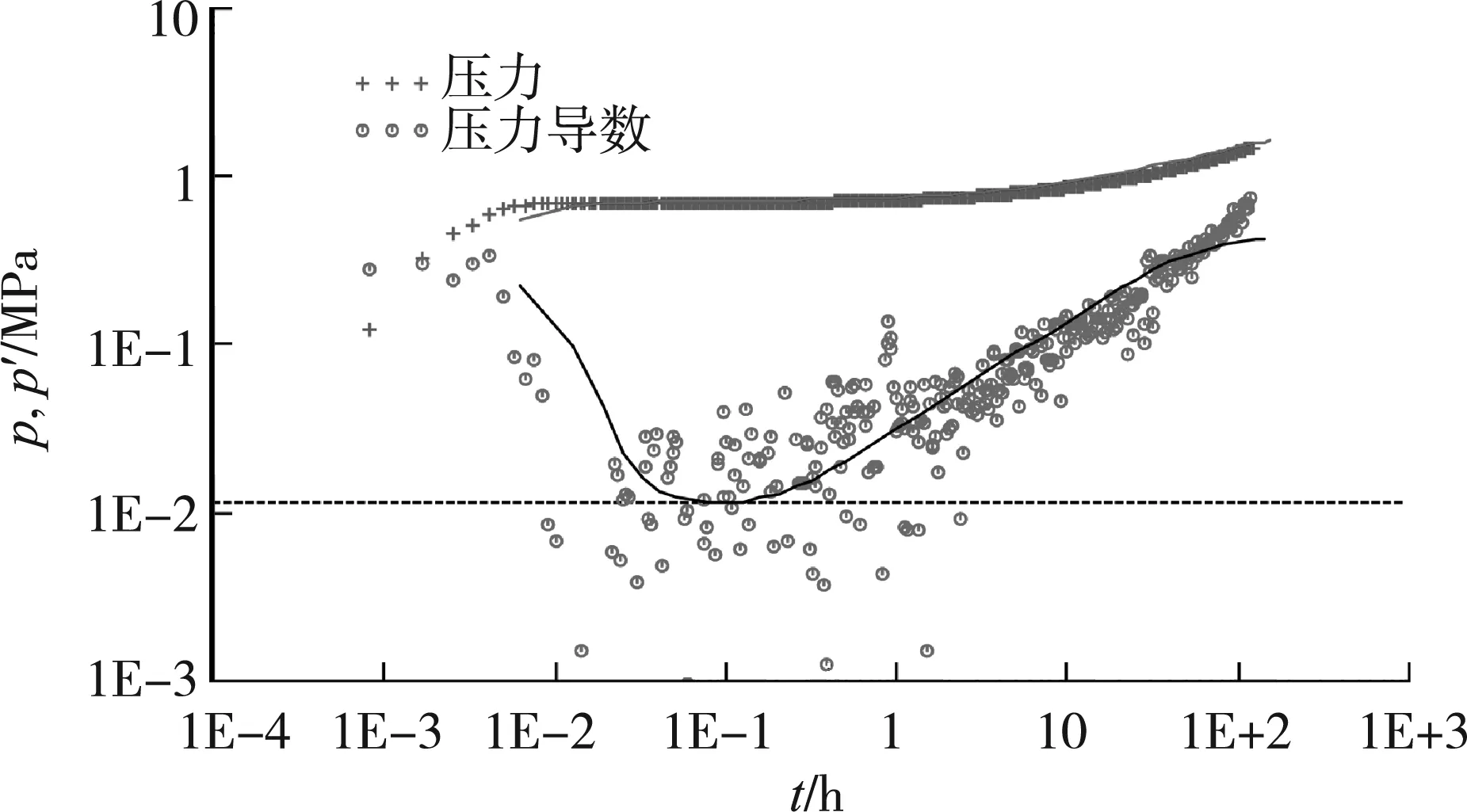
图1 YUEMa井双对数曲线拟合

结合静态地质情况，利用数值试井建立油藏平面属性模型(图2)，拟合双对数、压力历史曲线，并在分析拟合过程中反复调整反映各渗流区域特征的参数(流度比M、分散比D)，修正边界范围，最终得到：该井井控面积1.7 km2；内区地层系数为8.929 μm2·m，渗透率为1.509 μm2；1区渗透率为0.196 μm2，2区渗透率0.191 μm2，3区渗透率0.076 μm2，外区渗透率为0.004 μm2；同时得到各渗流区域储能比ω。根据式(1) — 式(3)分析各区域动态储量。利用Blasingame曲线拟合方法计算总动态储量为13.28×104t，其中，内区5.94×104t、1区 2.31×104t、2区2.25×104t、3区1.49×104t、外区1.29×104t。

(1)

(2)

(3)

式中：M—— 流度比；

K—— 渗透率，10-3μm2；

h—— 储层有效厚度，m；

μ—— 地下原油黏度，mPa·s；

D—— 分散比；

φ—— 孔隙度；

Ct—— 地层综合压缩系数，MPa-1；

ω—— 储能比。

通过数值试井分析YUEMa井，建立油藏模型，结合静态地质特征，得到不同区域储层的渗流特征及储能比。储层沿断裂展布，控制范围较大，采用降压开采可极大限度动用各区域储层潜力，提高最终采收率。

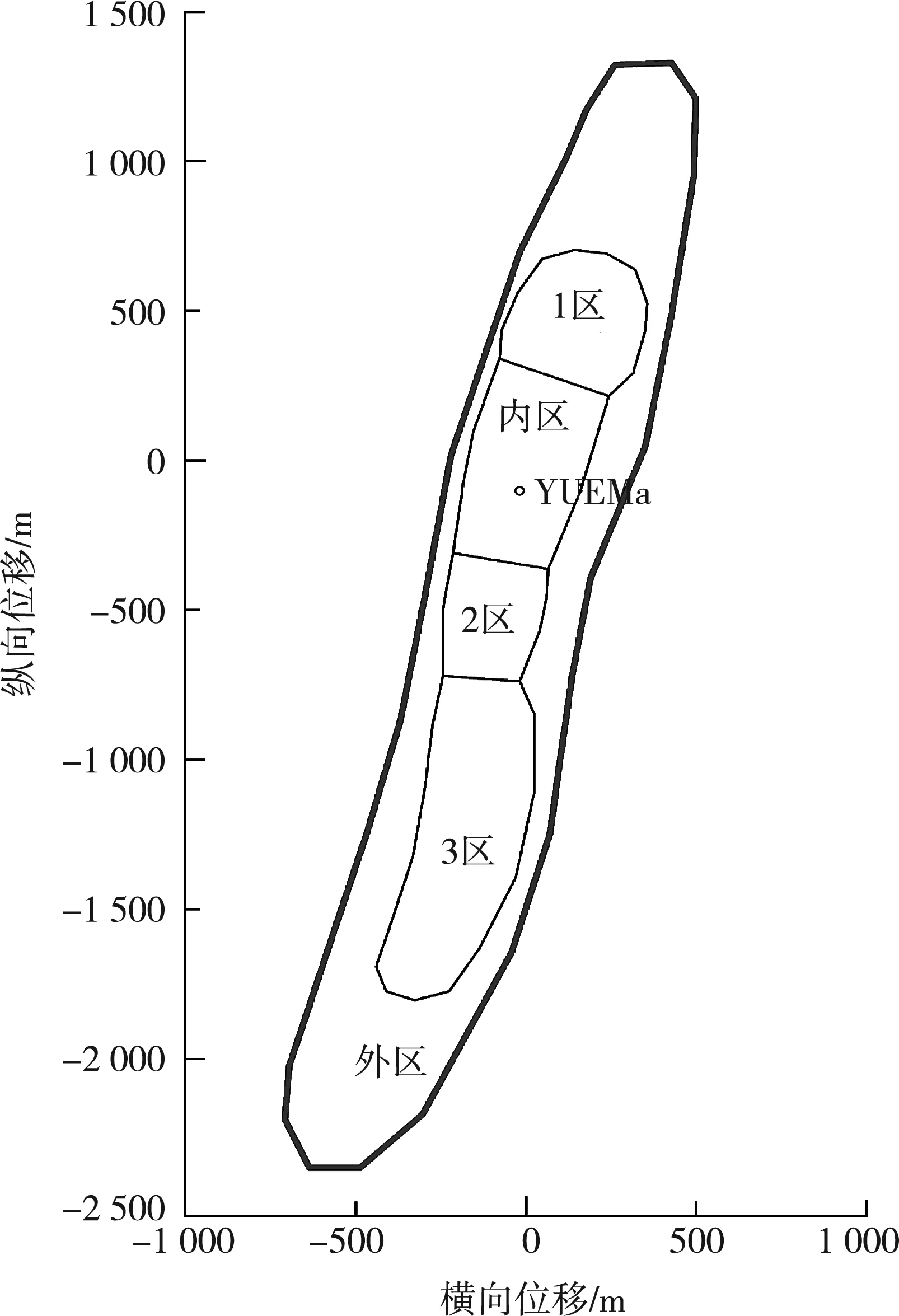
图2 YUEMa井数值试井平面属性模型

2.2 定容型应用分析

YUEMb井大型缝洞体由“串珠群+杂乱”状反射构成，呈长轴近南北向椭圆形态，面积0.68 km2。钻井至井深7 245.18 m时溢流0.3 m3，随即关井采用压回法压井，压井成功后强钻至井深7 248.46 m时又出现放空，井下情况复杂，因此提前完钻，未进行测井。

投产前进行压力恢复测试，双对数曲线反映储层为内好外差复合型特征(图3)。解析试井选择井储+表皮+四区径向复合储层+无限大拟合模型，分析得到：1区地层流动系数128.026(μm2·m)(mPa·s)、地层系数186.15 μm2·m、渗透率4.250 μm2，复合半径126 m；2区渗透率4.75×10-3μm2，复合半径178 m；3区渗透率0.31 ×10-3μm2，复合半径 237 m；4区渗透率0.25×10-3μm2。可以看出2、3、4区渗透率极低，该井近似于定容油藏。利用数值试井结合实际油藏地质特征构建油藏平面属性模型(图4)，拟合双对数、压力历史曲线，分析认为该井井控面积仅0.16 km2。利用Blasingame曲线拟合方法计算总动态储量9.04×104t，进而分别得到各区域渗流能力及动态储量：1区地层系数20.336 μm2·m、渗透率4.640 μm2、储能4.95×104t；2区渗透率8.000×10-3μm2、储能0.85×104t；3区渗透率10.000×10-3μm2、储能1.67×104t，外区渗透率5.000×10-3μm2、储能1.53×104t。

图4 YUEMb井数值试井平面属性模型

通过数值试井分析YUEMb井井控面积仅0.16 km2，定容特征明显，投产过程压力衰减快(平均每产140.9 t原油，井口油压降低1 MPa)。近井地带储层渗流能力好(地层系数为20.336 μm2·m)，储量分布集中于近井地带的缝洞体中，停喷后可注水替油提高采收率。

3 结 语

将数值试井技术与油藏地质特征描述紧密结合开展试井分析，能更细致评价油藏不同区域储层的渗流特征、储能情况并精细刻画油藏边界范围。

[1] 田冷，何顺利，施英.数值试井技术在凝析气藏边界识别中的应用[J].新疆地质，2009，27(1):95-97.

[2] 黄登峰，刘能强.数值试井在描述油气藏复杂边界中的应用[J].油气井测试，2006，15(6):18-19.

[3] 韩永新，庄惠农，孙贺东.数值试井技术在气藏动态描述中的应用[J].油气井测试，2006，15(2):9-11.

[4] 杨景海.数值试井解释应用流程及其正确性验证[J].油气井测试，2013，22(1):37-40.

[5] 刘立明，陈钦雷.单向流数值试井模型[J].油气井测试，2001，10(4):11-14.

[6] 王禹川，王怒涛，唐刚，等.哈拉哈塘地区缝洞型碳酸盐岩油藏单井生产特征[J].特种油气藏，2012，19(3):87-89.

[7] 陈利新，程汉列，高春海，等.哈拉哈塘油田碳酸盐岩储层试井特征分析[J].油气井测试，2015，24(2):16-18.

[8] 陈利新，程汉列，杨文明，等.哈拉哈塘碳酸盐岩储层试井与生产特征分析[J].断块油气田，2015，22(4):501-504.

Numerical Well Test Research in Halahatang Carbonate Reservoir

CHENGHanlie1,2WANGLianshan2WANGJianmin1LIUYong3ZHUYi3ZHANGLei2

(1. School of Earth Sciences and Engineering, Xi′an Shiyou University, Xi′an 710065, China; 2. LandOcean Energy Services Co. Ltd., Korla Xinjiang 841000, China; 3. Development Department of Tarim Oilfield Company, Korla Xinjiang 841000, China)

This paper discusses complexity of well testing interpretation for fracture-vug carbonate reservoir and the limitations of conventional well test based on Halahatang carbonate reservoir characteristics. Numerical well testing technology can be well combined with reservoir geological features to construct finite element numerical well testing model for fitting analysis to determine the reservoir parameters, calculate the OGIP and analysis of reservoir boundary features in different seepage zone. This paper also puts forward measures for the two typical types of reservoir in the study area: large area with multiple holes and constant volume control area. The application examples show that the numerical well testing technique can more effectively describe the real situation of reservoir, and it also provides theoretical basis for the later development measures.

fracture-vug reservoir; numerical well test; seepage characteristics; well stimulation

2016-02-11

国家科技重大专项“塔里木碳酸盐岩油藏重大开发试验”(2011ZX05004-004)

程汉列(1989 — )，男，工程师，西安石油大学在读硕士研究生，研究方向为油气藏工程及油气田动态分析。

TE353

A

1673-1980(2016)05-0035-04