反应位移法抗震设计中地基弹簧系数取值的探讨

丁德云， 杨秀仁

(1.北京城建设计发展集团股份有限公司，北京 100037; 2.北京九州一轨隔振技术有限公司，北京 100070)



反应位移法抗震设计中地基弹簧系数取值的探讨

丁德云1,2， 杨秀仁1

(1.北京城建设计发展集团股份有限公司，北京 100037; 2.北京九州一轨隔振技术有限公司，北京 100070)

随着城市轨道交通工程抗震性能越来越受到关注，反应位移法作为一种简捷的抗震设计方法被大量应用于地下结构抗震设计中。地基弹簧系数的确定方法是反应位移法抗震设计中最为重要的因素之一，本文选取试验法、李英民法、MIDAS法和有限元法，结合北京典型地层，对比分析这四种方法地基弹簧系数取值对地下结构的弯矩、轴力和剪力的影响规律。结果表明：(1)在反应位移法计算中，地基弹簧系数取值对结构内力响应具有重要影响，对结构轴力和剪力的影响较大，而对于弯矩的影响相对较小；(2)地基弹簧系数获取方法优选试验法，在无地勘资料情况下，经验公式和有限元法可作为备选方法；(3)综合考虑四种不同地基弹簧系数确定方法对结构内力影响程度，为保证结构设计的安全性，可对试验法下结构内力进行系数修正，修正系数建议值为1.10。

抗震设计； 地基弹簧； 反应位移法； 地下结构

0 引言

城市轨道交通工程作为城市生命线工程的重要组成部分，自2008年汶川地震后，其抗震性能问题越来越受到关注。特别是在住建部发布建质[2011]13号文件《市政公用设施抗震设防专项论证技术要点(地下工程篇)》后，地下结构抗震性能分析与验算越来越受到研究和设计人员的重视。城市轨道交通相关的抗震设计规范，诸如上海地标DG/TJ08-2064-2009、北京地标DB11/995-2013及国标GB50157-2013和GB50909-2014等陆续实施，对地下结构的抗震设计具有整体和方向性的指导意义[1-4]。但我国地下结构抗震设计起步比较晚，相关理论技术研究相对滞后。

国内用于城市轨道交通工程地下结构抗震性能分析的方法主要有连续介质模型法和“荷载-结构”模型法[5-9]两大类。前者将地下结构和周围土体视为整体共同受力，主要采用动力时程分析法，计算耗时长，一般设计人员不易掌握；后者将地下结构简化为Winkler弹性地基上的梁，通过地基弹簧的弹性抗力模拟周围土层对结构的作用，通常采用地震系数法、反应位移法等，计算耗时短，设计人员较容易掌握。国内外学者对反应位移法作了大量的研究，特别是针对假定条件、适用范围和参数取值等方面[10-13]。目前，反应位移法已广泛应用于地下结构的抗震计算分析中。

由于抗震问题的复杂性，目前还没有一种方法能够完全实现对地下结构动力反应进行全面而真实的解释和模拟。正是由于这种原因，在利用反应位移法进行抗震设计时应对输入的参数进行甄别。地基弹簧刚度作为反应位移法中重要的参数之一，其确定方法较多，本文重点针对该系数的取值进行相关探讨，以期为抗震设计提供参考。

1 地基弹簧系数的确定方法

国内外学者做了大量关于地基弹簧系数确定方法的研究，主要有经验公式法(李英民法和MIDAS法)、有限元法及试验法等。本文列举出几种典型的获取地基弹簧系数的方法。

1.1 试验法

试验方法包括现场试验和室内试验[14]。现场试验一般采用K30方法，即采用直径30 cm的荷载板进行垂直或水平加载试验，可直接测定水平和垂直地基弹簧系数。室内试验一般采用三轴试验或者固结试验的方法测得地基弹簧系数，在初步勘察阶段可根据地基土的分类、密实度进行参考值的选取，在详细勘察阶段应通过试验方法确定。

1.2 李英民法

李英民等[15]根据Vesic和Biot的相关地基弹簧系数及其他相关研究成果，以有限元分析结果为数据基础，采用数据拟合的方法，建立如下适用于地下结构抗震简化计算的法向和切向地基弹簧系数的经验计算公式：

底板法向和切向弹簧：

(1)

(2)

侧墙法向和切向弹簧：

(3)

(4)

式中：ρ为密度;cS为剪切波波速;v为泊松比;B为结构横截面宽度;H为结构横截面高度;h为结构底板至基岩面土层厚度;a1、a2、a3、a4、b1、b2、b3和b4分别为系数。

1.3MIDAS法

MIDAS/GTS手册[16]中采用用于地下结构动力分析的三维黏弹性人工边界。地基弹簧系数为：

竖向弹簧系数：

(5)

水平弹簧系数：

(6)

式中：α为系数，一般取α=1;E为介质弹性模量;Av、Ah分别为介质边界竖向和水平方向的截面积。

1.4 有限元方法

采用有限元法[1]建立地层-结构模型，在结构上施加法向和切向荷载Ph和Ps，获得结构的变形δh和δs，通过公式获得地基弹簧系数：

(7)

(8)

2 反应位移法模型

2.1 工程概况

某地下工程断面为框架结构，断面宽和高分别为10 m×7.6 m，结构顶板位于地下5 m。场地抗震设防烈度为Ⅷ度，设计地震分组为第一组，场地类型为Ⅲ类，设计基本地震加速度为0.2g，场地特征周期为0.45 s。

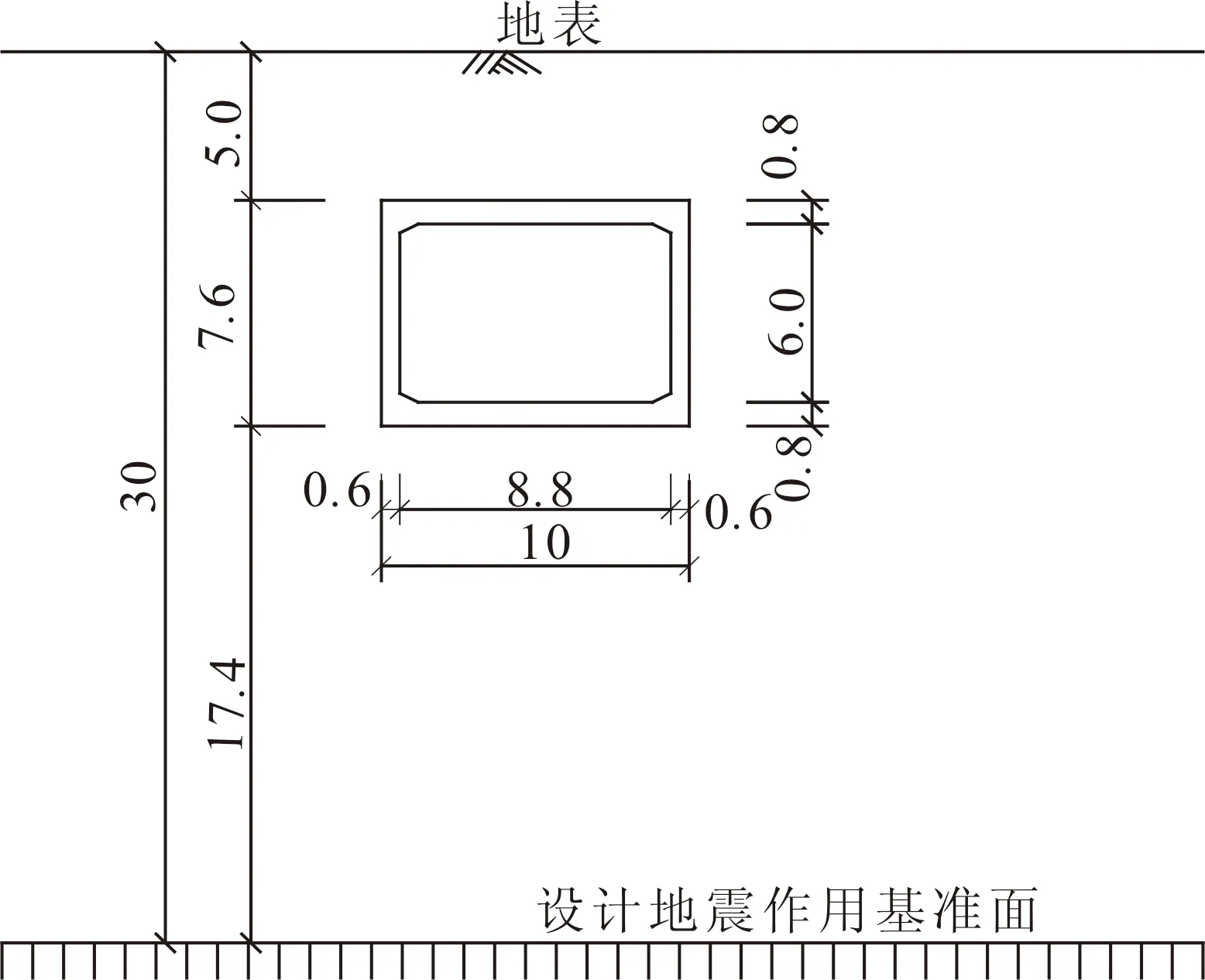
图1 地下结构横断面(单位：m)Fig.1 Cross section of underground structure (Unit: m)

为研究需要，选取北京地区典型地层参数,假定设计地震作用基准面以上土体为单一土层，考虑三种不同的土层参数(表1)。

表 1 土层物理力学参数

2.2 地基弹簧系数的取值

采用文中4种地基弹簧系数的确定方法进行法向和切向地基弹簧系数的取值(表2)。在试验法中，根据地勘数据，三种土层的竖向和水平地基弹簧系数分别为15和16、28和30、30和35 MPa。在李英民法中，选取推荐的系数获得三种土层的竖向和水平地基弹簧系数分别为10和7、18和13、42和30 MPa。在MIDAS法中，根据土层的弹性模量获得三种土层的竖向和水平地基弹簧系数分别为20和22、36和40、84和93 MPa。在有限元法中，对结构顶、底板和侧墙分别施加单位荷载获得对应位置的变形，对变形进行取平均值，按照推荐公式获得地基弹簧刚度。

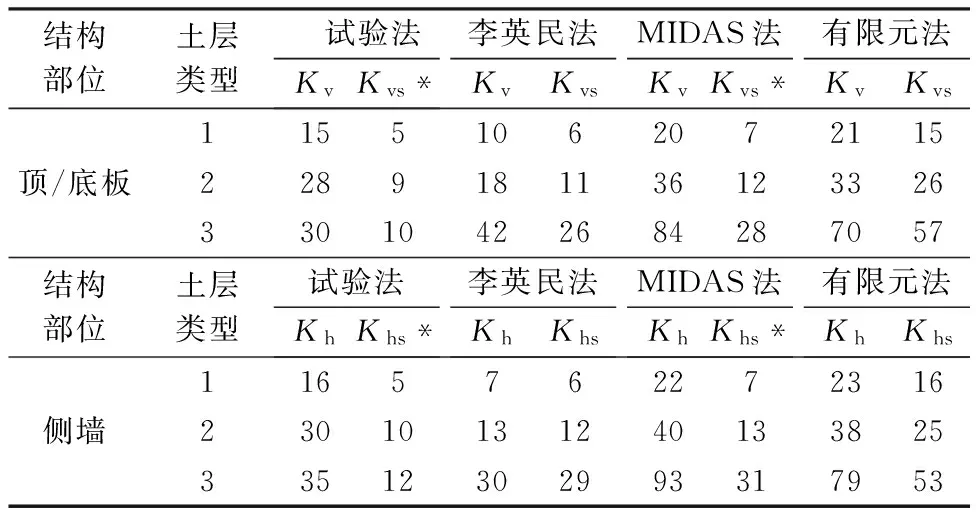
表 2 地基弹簧系数取值(单位：MPa/m)

注：Kv和Kh均是法向地基弹簧系数

Kvs和Khs均是切向地基弹簧系数

*表示切向地基弹簧系数为法向取值的1/3

2.3 地震荷载

在反应位移法中主要考虑土层相对位移引起的地震土压力、土层剪力以及结构惯性力3种地震作用。

将地层位移沿深度方向的变化假设为余弦函数，计算地层相对位移，然后计算出地震土压力。

土层变形计算按下式：

(9)

式中：umax为地表与基准面的相对最大位移;H为设计地震作用基准面的深度。

地层相对水平位移u'(z)根据下式可得：

(10)

式中：u(zB)为结构底板处的水平位移。

表3给出了结构不同埋深处节点水平位移u(z)和节点水平相对位移u'(z)。

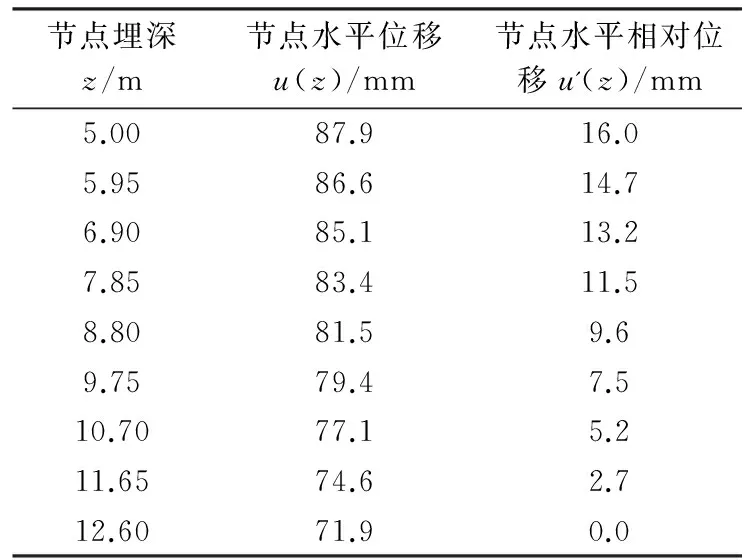
表 3 土层水平位移

地震土压力计算：

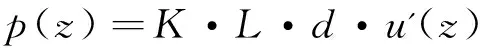
(11)

式中：K为地基弹簧系数；L为结构有限元网格尺寸；d为结构纵向计算长度，一般取d=1 m。

地震土层剪力[17]表示为：

(12)

(13)

(14)

式中：τU为结构顶板单位面积上的剪力;τB为结构底板单位面积上的剪力;τS为结构侧墙单位面积上的剪力;Gd为土层的动剪切模量;Tg为场地特征周期;Sa为设计基本地震加速度。

表4给出了三种类型土层下结构与土体之间在地震时的土层剪力。

结构惯性力可按下式计算：

(15)

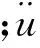
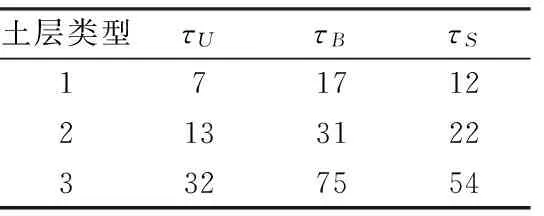
表 4 地震土层剪力(单位：kN/m)

经计算可得：侧墙的惯性力为3 kN/m，而顶底板的惯性力为4 kN/m。

3 结果分析

图2和图3分别给出了土层类型1和3下结构的弯矩云图。从图中可以看出：(1)在地震荷载作用下，结构弯矩呈现不对称性，正弯矩最大值出现在结构左侧墙中上部，而负弯矩最大值出现在结构左侧墙底部和结构底板左端；(2)总的来说，MIDAS法和有限元法下结构弯矩值较接近，试验法次之，而李英民法最小。土层类型2和土层类型1中结构的弯矩分布规律相似，量值差异较大。表5列出了三种土层类型下结构弯矩最大值的统计值。

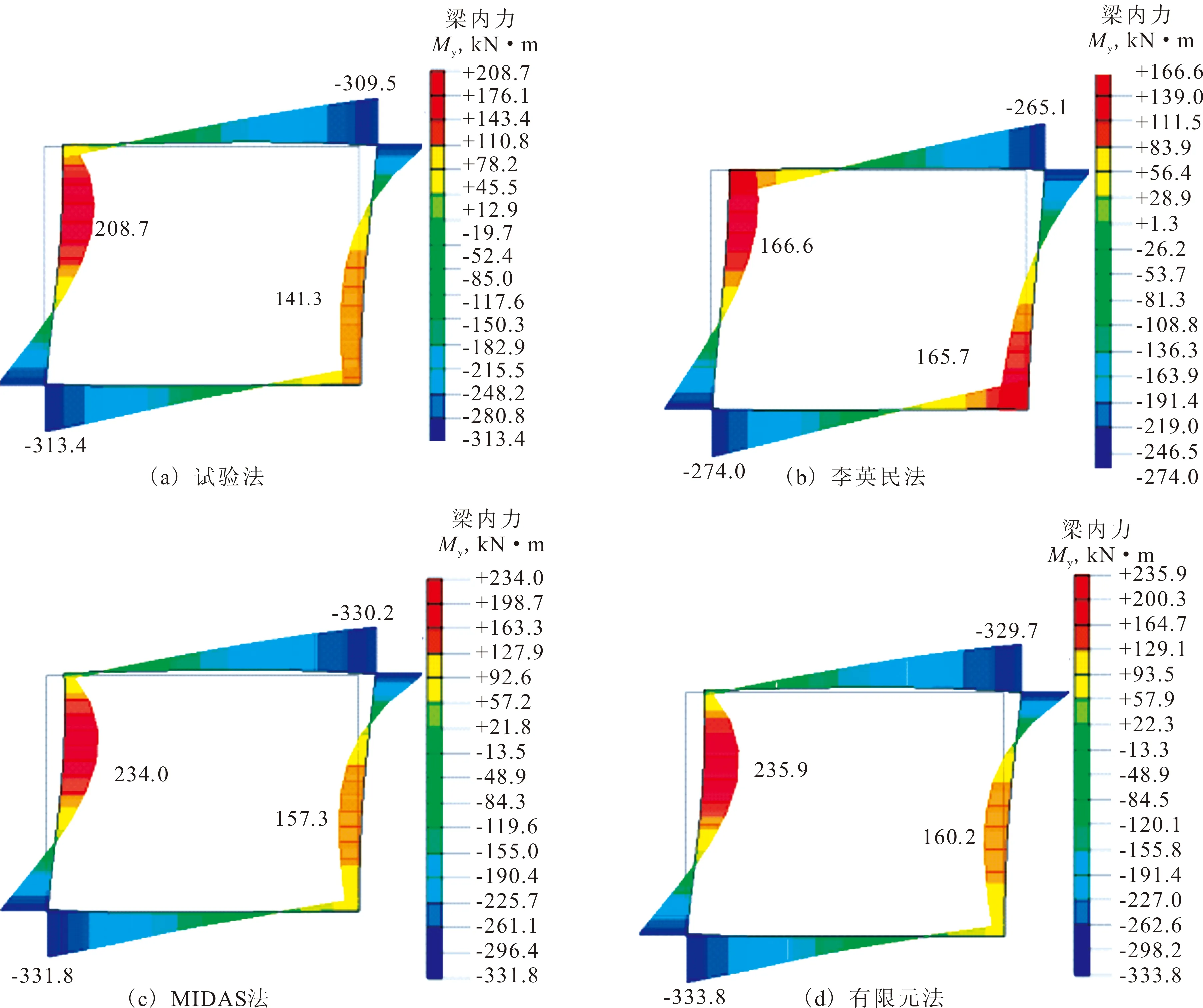
图2 土层类型1下结构的弯矩(单位: kN·m)Fig.2 Bending moment of the structure in soil 1 (Unit: kN·m)

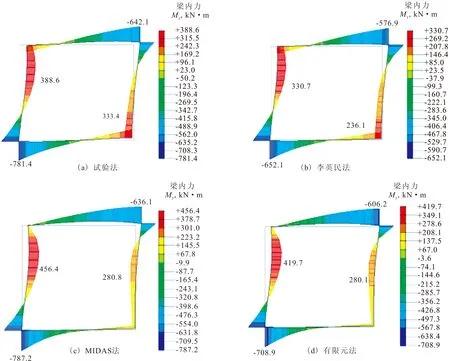
图3 土层类型3下结构的弯矩(单位: kN·m)Fig.3 Bending moment of the structure in soil 3 (Unit: kN·m)

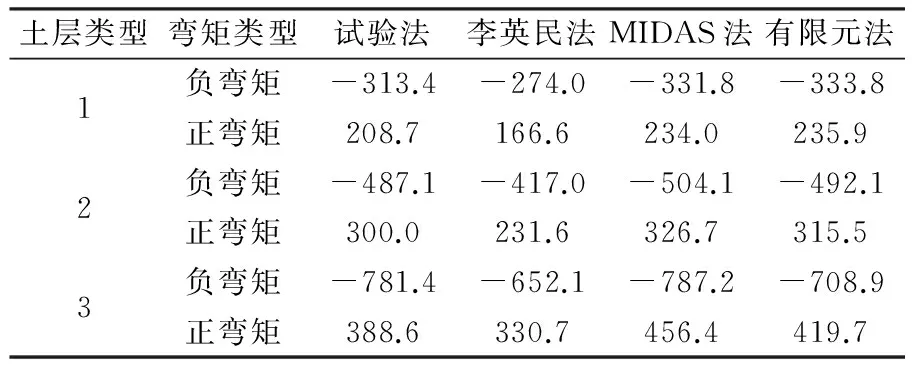
表 5 结构弯矩最大值统计(单位：kN·m)

为了便于比较4种不同地基弹簧系数取值对结构内力的影响，对结构弯矩最大值进行归一化处理，以试验法下弯矩结果作为归一化对象，见表6。从表中可以看出：(1)李英民法下归一化数值均小于1，而MIDAS法和有限元法则绝大多数值大于1，且二者数值较接近；(2)李英民法、MIDAS法和有限元法相对试验法误差均值分别为-17%，8%和4%。

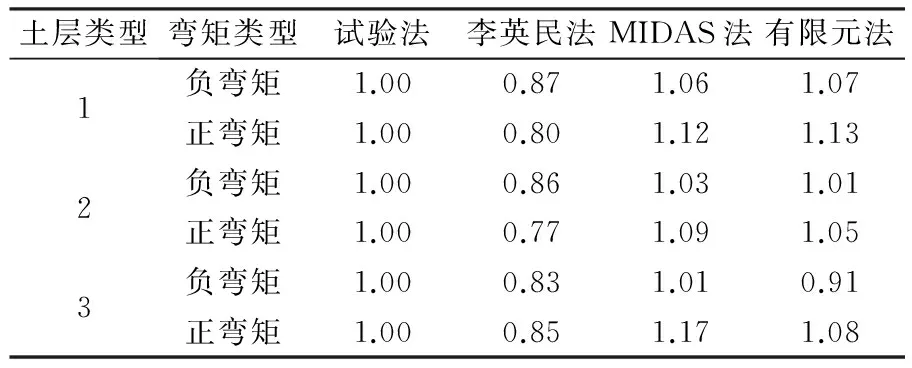
表 6 结构弯矩最大值归一化统计

图4给出了土层类型3下结构的轴力云图。从图中可以看出：(1)在地震荷载作用下，结构轴力呈现非对称性，受压轴力最大值出现在结构顶板右端，而受拉轴力出现在结构侧墙和底板局部；(2)总的来说，MIDAS法和有限元法下结构轴力值较接近，试验法次之，而李英民法最小。土层类型1和2中结构的轴力分布规律与地层类型3相似，量值差异较大。

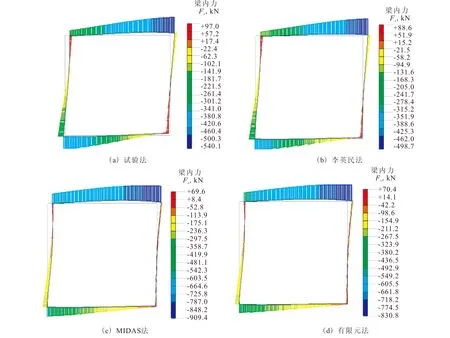
图4 土层类型3下结构的轴力(单位: kN)Fig.4 Axial force of the structure in soil 3 (Unit: kN)

表7列出了三种土层类型下结构轴力最大值归一化的统计值。从表中可以看出：(1)李英民法下归一化数值均小于1，而MIDAS法和有限元法下的数值均大于1，且二者数值较接近；(2)李英民法、MIDAS法和有限元法相对试验法误差均值分别为-29%，37%和32%。

图5给出了土层类型3下结构的剪力云图。从图中可以看出：(1)在地震荷载作用下，结构剪力呈现非对称性，剪力最大值出现在结构右侧墙上端部；(2)总的来说，MIDAS法和有限元法下结构剪力值较接近，试验法次之，而李英民法最小。土层类型1和2中结构的剪力分布规律与地层类型3相似，量值差异较大。

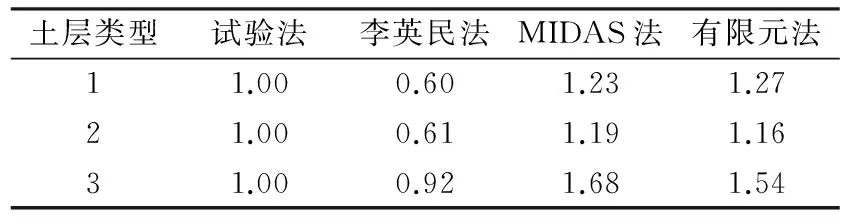
表 7 结构轴力最大值归一化统计

表8列出了三种土层类型下结构剪力最大值归一化的统计值。从表中可以看出：(1)李英民法下归一化数值均小于1，而MIDAS法和有限元法下的数值均大于1，且二者数值较接近；(2)李英民法、MIDAS法和有限元法相对试验法误差均值分别为-26%，29%和25%。

从以上4种不同地基弹簧系数确定方法对结构弯矩、轴力和剪力影响分析中可以看出，经验公式法和有限元法相对试验法而言，会在一定程度上放大或者缩小结构内力。为保证结构设计的安全性，可对试验法下结构内力进行系数修正，综合弯矩、轴力和剪力误差以及设计中通常将地下结构以压弯和纯弯构件考虑，可将修正系数设为1.10。

图5 土层类型3下结构的剪力(单位: kN)Fig.5 Shear force of the structure in soil 3 (Unit: kN)

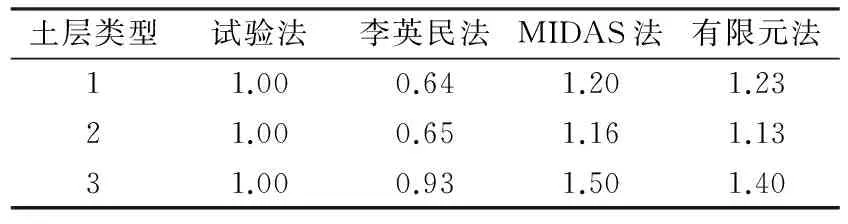
表 8 结构剪力最大值归一化统计

4 结论

通过对反应位移法在城市轨道交通地下结构抗震设计中采用不同的地基弹簧系数取值进行探讨，综合分析结构内力变化规律，得出如下结论：

(1) 在反应位移法计算中，地基弹簧系数取值对结构内力响应有重要影响，对于结构轴力和剪力的影响较大，而对于弯矩的影响相对较小。

(2) 地基弹簧系数获取方法优选试验法，在无地勘资料情况下，经验公式和有限元法可作为备选方法。

(3) 综合考虑4种不同地基弹簧系数确定方法对结构内力影响程度，为保证结构设计的安全性，可对试验法下结构内力进行系数修正，修正系数建议值为1.10。

References)

[1] 同济大学，上海申通轨道交通研究咨询有限公司.DG/TJ08-2064-2009,地下铁道建筑结构抗震设计规范[S].上海：上海市建筑建材业市场管理总站，2009.

Tongji University, Shanghai Shentong Metro Research Consulting Co.,Ltd..DG/TJ08-2064-2009,Code for Seismic Design of Subway Structure[S].Shanghai:Shanghai Building Materials Industry Market Management Bureau,2009.(in Chinese)

[2] 北京城建设计研究总院有限责任公司.DB11/995-2013，城市轨道交通工程设计规范[S].北京：北京市质量技术监督局，北京市规划委员会，2013.

Beijing Urban Engineering Design and Research Institute Co.,Ltd..DB11/995-2013, Code for Design of Urban Rail Transit[S].Beijing:Beijing Quality and Technical Supervision,Beijing Municipal Commission of Urban Planning,2013.(in Chinese)

[3] 中华人民共和国住房和城乡建设部.GB50157-2013，地铁设计规范[S].北京：中国建筑工业出版社，2013.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB50157-2013, Code for Design of Metro[S].Beijing:China Architecture and Building Press,2013.(in Chinese)

[4] 中华人民共和国住房和城乡建设部.GB50909-2014，城市轨道交通结构抗震设计规范[S].北京：中国计划出版社，2014.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China.GB50909-2014, Code for Seismic Design of Urban Rail Transit Structures[S].Beijing: China Planning Press,2014.(in Chinese)

[5] Kiyomiya O.Earthquake-resistant Design Features of Immersed Tunnels in Japan[J].Tunneling and Underground Space Technology，1995，10(4):463-475.

[6] Hashash Y M A，Hook J J，Schmidt B，et al.Seismic Design and Analysis of Underground Structures[J].Tunneling and Underground Space Technology，2001，16(4):247-293.

[7] 边金，陶连金，张印涛，等.地下结构抗震设计方法的比较与分析[J].现代隧道技术，2008，45(6):50-55.

BIAN Jin，TAO Lian-jin，ZHANG Yin-tao，et al.Comparison and Analysis of the Aseismic Design Methods for Underground Structures[J].Modern Tunneling Technology，2008，45(6):50-55.(in Chinese)

[8] 宋林，孟昭博，吴敏哲，等.双层岛式地铁车站结构地震反应分析[J].世界地震工程，2010，26(2):187-192.

SONG Lin，MENG Zhao-bo，WU Min-zhe，et al.Dynamic Response Analysis of a Two-layer Subway Station Structure under Earthquakes[J].World Earthquake Engineering，2010，26(2):187-192.(in Chinese)

[9] DING De-yun,WANG Wei-feng,HUANG Mei-qun，et al.Time-history Analysis of Seismic Performance of Metro Station by Top-down Boring with Cast-in-situ Arch[J].Applied Mechanics and Materials，2013，256-259:2216-2221.

[10] WANG J N.Seismic Design of Tunnels:A Simple State-of-the-art Design Approach[M].New York:Parsons Brinckerhoff Quade and Douglas Inc，1993.

[11] 黄先锋.地下结构的抗震计算——位移响应法[J].铁道建筑，1999(6):3-6.

HUANG Xian-feng.Seismic Calculation of Subway Structures——Response Displacement Method[J].Railway Engineering，1999(6):3-6.(in Chinese)

[12] 刘晶波，王文晖，张小波，等.地下结构横断面地震反应分析的反应位移法研究[J].岩石力学与工程学报，2013，32(1)：161-167.

LIU Jing-bo，WANG Wen-hui，ZHANG Xiao-bo，et al.Research on Response Deformation Method in Seismic Analysis of Underground Structure[J].Chinese Journal of Rock Mechanics and Engineering，2013，32(1):161-167.(in Chinese)

[13] 王国波，王敏，覃程，等.对反应位移法中几个关键问题的探讨[J].地下空间与工程学报，2014，10(6):1367-1371，1386.

WANG Guo-bo，WANG Min，QIN Cheng，et al.Investigation on Several Key Issues of Response Displacement Method[J].Chinese Journal of Underground Space and Engineering，2014，10(6):1367-1371，1386.(in Chinese)

[14] 中华人民共和国住房和城乡建设部.GB50307-2012,城市轨道交通岩土工程勘察规范[S].北京：中国计划出版社，2012.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China.GB50307-2012, Code for Geotechnical Investigation of Urban Rail Transit[S].Beijing:China Planning Press,2012.(in Chinese)

[15] 李英民，王璐，刘阳冰，等.地下结构抗震计算地基弹簧系数取值方法研究[J].地震工程与工程振动，2012，32(1):106-113.

LI Ying-min，WANG Lu，LIU Yang-bing，et al.Analysis of Methods for Determining the Spring Constant of Ground Foundation in Seismic Design of Subway Structures[J].Journal of Earthquake Engineering and Engineering Vibration，2012，32(1):106-113.(in Chinese)

[16] 北京迈达斯技术有限公司.MIDAS/GTS技术手册[M].北京：北京迈达斯技术有限公司，2005.

Beijing MIDAS Information Technology Co.,Ltd.MIDAS/GTS Technical Manual[M].Beijing:Beijing Midas Information Technology Co.,Ltd.,2005. (in Chinese)

[17] 川岛一彦.地下构筑物的耐震设计[M].日本：鹿岛出版社，1994.

KAWAJIMA Kazihiko.Aseismic Design of Underground Structure[M].Japan:Kajima Institute Publishing Co.,Ltd.,1994.(in Japanese)

Discussion on the Spring Constant of Ground Foundation in the Seismic Design of Underground Structures Using the Response Displacement Method

DING De-yun1, 2, YANG Xiu-ren1

(1.BeijingUrbanConstructionDesign&DevelopmentGroupCo.,Limited,Beijing100037,China;2.BeijingJiuzhouyiguiShock&VibrationIsolationTechnologyCo.,Ltd.,Beijing100070,China)

Urban rail engineering faces significant challenges with regard to an earthquake resistant design of underground structures. The response displacement method is a simple method, which is widely used to design such structures. Thus, determining the ground spring constant in the seismic design of underground structures is very important. Four typical determination methods are introduced: the test method, Li’s method, the MIDAS method, and the finite element method. Based on the values of the ground spring constant determined through these four methods and considering the local geological conditions in Beijing, response displacement models are used to obtain the bending moment, axial force, and shear force of the underground structures. The four determination methods are compared on the basis of their respective advantages and disadvantages. The results show that the values of the ground spring constant have a significant influence on the internal force response of underground structures. Moreover, using the response displacement method, we observe that the constant has a greater influence on the axial force and shear force and comparatively lesser influence on the bending moment. The test method is recommended for designers, when geological survey data are not available. The empirical formula and the finite element method can be used as alternative methods. In order to ensure design safety, the internal force of underground structures can be modified by a correction factor of 1.10, considering that the four typical determination methods have an impact on the internal force.

seismic design; ground spring; response displacement method; underground structure

2016-04-26

北京市科学技术委员会科技新星计划(xx2016008)；北京城建设计发展集团股份有限公司科技创新计划(2015-18)

丁德云，男，博士，高级工程师，主要从事地下工程建造技术、结构抗震及运营环境影响研究。E-mail:dyding2301@163.com。

TU91

A

1000-0844(2016)05-0685-08

10.3969/j.issn.1000-0844.2016.05.0685