应用SPH方法实现海面孤立波运动的模拟*
2016-11-18欧训勇
欧训勇
(海南热带海洋学院 电子通信工程学院, 海南 三亚 572022)
应用SPH方法实现海面孤立波运动的模拟*
欧训勇
(海南热带海洋学院 电子通信工程学院, 海南 三亚 572022)
首先介绍孤立波的KdV方程,继而讨论了孤立波SPH方法的数值求解过程,选择SPH光滑核函数作为正则化高斯核函数。分析了数值求解过程的时间积分方法,给出了具体计算公式,最后给出相应程序中的具体参数下孤立波运动模拟效果。
孤立波;自由表面流体;SPH
0 引言
孤立波是1834年由RUSSELL S观察发现到的,而Korteweg和de Vies于1895第一次通过理论模型对孤立波进行了解释,被称为KdV理论。该理论基于弱色散浅水波理论,浅水波色散由非线性效果平衡,使得波在传播过程中在任意距离都保持着一定的振幅和形状。KdV方程的精确解描述了孤立子的形状和传播速度。尽管KdV理论被认为是一阶近似解,很好地描述了真正的孤立波,而高阶近似解也一样可以构成。参考文献[1]中介绍了任意高阶迭代,逐次逼近模型,在第一次迭代步骤中再现了KdV理论,然而,更高阶求解需要数值方法。
光滑粒子流体动力学(以下简称SPH)是一种无网格拉格朗日型数值方法,由LUCY L于1977年提出。该方法最初应用于天体物理学领域,然而受海岸工程问题所驱动,由MONAGHAN J J在1994第一次提出用于模拟流体流动。
在过去的二十多年中,由于在模拟流体自由表面流动有突出的性能,SPH方法成为工程应用领域最流行的粒子数值方法,例如近海波模拟、海啸。本文讨论利用SPH方法实现海面孤立波运动的三维模拟效果。
1 孤立波的方程
孤立波传播的零阶近似解可以用线性波方程描述,而浅水中的波速由以下式子给出:
(1)
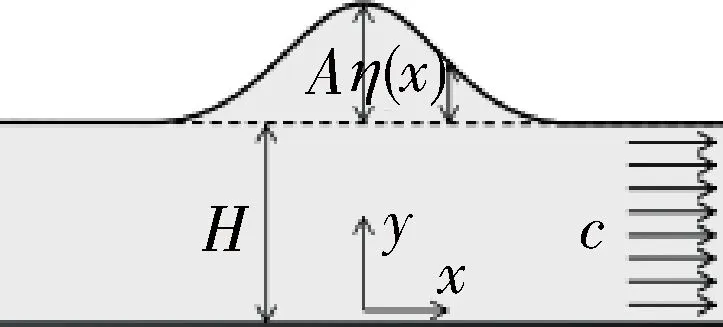
图1 孤立波传播图示
式中,g为重力加速度,H为水域的深度。式(1)给出了孤立波传播的一个粗略近似值,而忽略一些特殊的性能,如波的实际振幅和宽度,孤立波传播过程如图1所示。图1中A为波幅,η(x)是自由表面波形状函数。式(1)仅当A< 线性波的传播方程是没有孤立波解的。KdV方程如下: (2) 式(2)适用于以不同几何结构构造自由表面孤立子的形状。函数η(x,t)表示给定位置x的表面高度,是一个与时间有关的函数。单个自由表面孤立波的KdV方程的精确解由波的形状函数给出,如下: η(x)=Ach-2(k(x-a)) (3) 式中,A是振幅,a是孤立子水平偏移量,k为有效的波数,其取值如下: (4) 一阶孤立波的传播速度计算公式为: (5) 二阶孤立波的传播速度由HAL′ASZ G B做了修正[2],其公式如下: (6) 在流体力学中,广泛应用欧拉方程和连续方程来描述流体运动。描述流体运动的偏微分方程中,局部和对流通量都包含在拉格朗日微分方程中,如下式: (7) 其中,Φ表示一个任意的标量或矢量场。利用上式的微分算子可以得到无粘性流体力学方程如下: (8) 式(8)中的v、ρ、P、v、g分别指流体的速度、密度、压力、运动粘度和重力加速度。在弱可压缩流体中式(9)被定义为流体密度和压力之间的关系: p=p(ρ) (9) 尽管上述各类方程包括偏微分方程、波传播方程等有解析解,但是通常情况下仍不能得证通过恰当的数值方法得到精确解,只能得到某种程度上的近似解。然而,这些近似方法经常取得不利的数值特性,因此它们的一般性、鲁棒性、实用性都受限制。考虑层流的无粘性,现今的动力流体建模都尽量避免对复杂湍流模型建模。 3.1 SPH方程 无网格拉格朗日数值方法称为光滑粒子流体动力学是一种适用于解决式(8)方程系统的工具。SPH近似数值方法是基于流体节点,该节点称为粒子,它们在空间中运动时,每个粒子都携带有相应的物理量,如质量、密度、压力、速度等。这种离散方法是基于受域加权插值的,在一个给定的点,使用临近区域内的粒子,这些粒子受一个称为光滑核函数W(ri-rj,h)的控制,形成一个离散卷积。其函数如下: (10)式中,i指当前粒子,j是邻域内的一个粒子,fi=f(ri)是任意流场中粒子i的位置ri,核函数Wij=W(ri-rj,h)带有紧支性或无限影响半径,h称为光滑长度,Vj是指定粒子j的物理量值,N是核函数Wij影响范围内的粒子数。公式(10)以离散化构造一个任意流场,流场以粒子散布在空间里。文中讨论的计算过程即正则化高斯核函数[3],公式如下: (11) 式(11)为改进的高斯核函数。式中r=|ri-rj|。常量C0和C1由下式计算: (12) 本文讨论中,影响域δ取值为3h。相应地,两个一阶微分算子梯度和旋度如下: (13) 在SPH数值方法中通过插入数值扩散项到连续运动的方程中以保持数值稳定性是一种较流行的实践方法。由于自由表面孤立子受惯性力驱动,表现出粘性行为,动量扩散(物理数值)在目前的工作中可以忽略。相反,在连续方程中密度的数值扩散项是由文献[3]算出来的,在参考文献[4]中得以改善。参考文献[4]中ANTUONO M提出的基于线性稳定分析,密度扩散项成为一个高效的数值阻尼振荡工具。 可压缩性作为另一种特殊的SPH数值属性,可受控于近似弱可压缩流体方程,这种状态假设一个正压流体的压力和密度之间的线性关系。本文使用的SPH数值方法的离散动力学方程如下: (14) 式(14)中,ρ0是参考密度值,f是外力之和(包括重力),cs是声波传播速度。第一公式右边第二项是人工密度扩散项,在建模中常称为δSPH,经验系数ξ=0.1。Ψij项的计算公式如下: (15) (16) 式(16)中⊗表示张量积。正则张量L在流体边界影响着离散拉普拉斯收敛,它以修正由内核截断引起的离散梯度人工数值达到收敛目的。 要降低计算量,弱可压缩流体模型通常运行在声速范围,但是其量要足够大,以保持在预定义范围、独立惯性和声波内有足够大的绝对密度偏差。通常取值较现在经典流体速度幅值的10倍大,其计算公式和式(1)相差10倍,具体如下: (17) 式(17)中M取值为10。 利用SPH方法实现孤立波运动的模拟效果,整个实现过程涉及求解孤立波SPH数值解,确定SPH的边界及初始条件,以及孤立波运动的时间积分过程。 3.2 SPH方法的边界和初始条件 SPH方法的显著效益(至少在流体建模中)是把任意自由曲面当作自然边界处理而不需要任何额外的计算负担。另外,如果流体简单地连接着空气,完全可以从计算域中忽略,因为是恒压和水密度量。注意,在复杂流动情况下,如破浪,空气可能起着重要作用,因此它不应该被忽视。本文中应用两种SPH不同的边界条件:一种是边界墙体和底部,另一种是周期性的边界,允许在无限领域执行更一般的计算[5-6]。 这里的周期边界的基本量是在翼展方向形成的2D宽域展向近似平面,带有三维求解。在SPH的固体边界的模型中有几个基础性质的变种。 3.3 SPH方法的时间步积分 式(14)可以通过任意形式求解,是稳定的数值解析方法。本文研究应用二阶预修正方法,第一步粒子按△t/2,具体计算公式如下: (18) 在中间状态,密度导数、压力、外力、粒子内力(加速度)进行近似估算。使用新的数值以全步时间长度推进粒子运动,其计算公式如下: (19) 为了降低计算性能的要求,保持数值稳定,时间步长可以在每帧中自适应选择。在当前的SPH模型使用CFL条件执行计算。 (20) 上式中,CFL=0.2,Vij=Vi-Vj 图2 运行效果 根据以上各节介绍的方程及数值求解的过程,利用OpenGL三维图形库,在C-free 5环境下,使用C++面向对象的编程方法实现了对在浅水滩运动的孤立波模拟。由于考虑计算量,SPH程序使用粒子总数为4 096个,即为4K。粒子质量为0.000 205 43,密度为600,光滑长度为0.01,粒子半径0.004,粒子影响间距为0.005 9,流体黏度系数为0.2。程序运行效果截图如图2所示。 程序运行环境为:Intel(R) Core(TM) i3-2348M @ 2.30 GHz CPU,4 GB内存,模拟的海浪孤立波运行效果非常流畅。以上方法实现的算法中SPH粒子数量可达8 000个以上。超过8 000个粒子后,可看到模拟动画效果出现卡顿了。要想达到更大的粒子数量,采用GPU方法能取得更佳效果。本研究在应用于构建模拟大水域海浪运动,将继续深入探索GPU方法及网络分块协同渲染描绘更大水域波浪运动。研究成果将应用于构建光滑粒子流体动力学方法下的船舶运动的虚拟仿真系统。 [1] MOLTENI D, COLAGROSSI A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH[J]. Computer Physics Communications, 2009,180(6): 861-872. [2] HAL′ASZ G B. Higher order corrections for shallow-water solitary waves: elementary derivation and experiments[J]. European Journal of Physics, 2009,30(6):1311-1323. [3] ANTUONO M, COLAGROSSI A, MARRONE S, et al. Free-surface flows solved by means of SPH schemes with numerical diffusive terms[J]. Ccomputer Physics Communications,2010,181(3):532-549. [4] ANTUONO M, COLAGROSSI A, MARRONE S. Numerical diffusive terms in weakly-compressible SPH schemes[J]. Computer Physics Communications, 2012,183(12):2570-2580. [5] 刘瑛琦. 基于SPH方法的数值波浪水槽研究[D].南京:河海大学,2006.[6] 高睿,任冰,王国玉,等. 孤立波浅化过程的SPH数值模拟[J]. 水动力学研究与进展(A辑),2010,25(5):620-629. Simulating solitary waves with SPH Ou Xunyong (School of Electronics and Communication Engineering, Hainan Tropical Ocean University, Sanya 572022, China) In this paper, we first introduce the KdV equation of the solitary wave, and then discuss the numerical solution of the SPH method. We choose the regularized Gauss kernel function as the kernel functions of SPH. Then we analyze the numerical solving process time integral method, and give the specific calculations. Finally, the simulation results of the solitary waves motion under the specific parameters of the program are given. solitary waves; free-surface fluid; SPH 海南省自然科学基金项目(20166226) TP311.1 A 10.19358/j.issn.1674- 7720.2016.20.019 欧训勇. 应用SPH方法实现海面孤立波运动的模拟[J].微型机与应用,2016,35(20):69-71,74. 2016-05-25) 欧训勇(1976-),通信作者,男,硕士,副教授,主要研究方向:OpenGL三维图形技术、虚拟现实技术。E-mail:ouxy_1976@126.com。2 流体控制方程
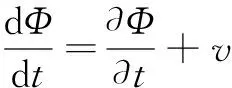
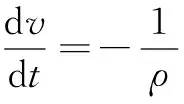
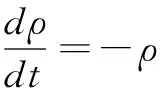
3 孤立波的SPH数值模拟
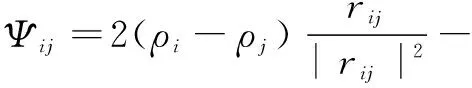

4 程序运行结果
5 结论
