基于改进hp自适应伪谱法的高超声速飞行器上升段轨迹规划
2016-11-18刘瑞帆于云峰闫斌斌
刘瑞帆, 于云峰, 闫斌斌
(西北工业大学 航天学院, 陕西 西安 710072)
基于改进hp自适应伪谱法的高超声速飞行器上升段轨迹规划
刘瑞帆, 于云峰, 闫斌斌
(西北工业大学 航天学院, 陕西 西安 710072)
针对高超声速飞行器的上升段轨迹优化问题,提出了一种改进的hp自适应Radau伪谱法。该算法将轨迹划分为多个子区间,采用双层优化策略迭代调整子区间个数和区间内的配点数。首先,以微分-代数约束在采样点处的相对误差作为解的误差评估准则;在需要提高精度的区间,将相对误差作为迭代判据,若通过相对误差求得的多项式阶数小于允许的最大阶数,增加区间内的配点数(p法);否则,细化时间区间(h法)来提高求解精度。仿真结果表明,相较于h方法和p方法,文中的算法在求解最优问题时配点总数更少,求解效率更高。
上升段;轨迹优化;hp自适应;伪谱法;高超声速飞行器
飞行器轨迹优化是指在特定的约束条件下,寻找飞行器从初始点到目标点满足某种性能指标最优的运动轨迹。在数学本质上,飞行器轨迹优化可以抽象为在包含微分方程、代数方程和不等式等约束下求解泛函极值的开环最优控制问题。一般将轨迹优化方法分为直接法和间接法,间接法基于Pontryagin极大值原理将最优控制问题转换为Hamiltonian边值问题(HBVP),其解的精度高,满足一阶最优必要条件,但HBVP问题的收敛域小,需要估计协态变量的初值,且难以求解存在路径约束的最优控制问题[1-3];直接法无需求解最优必要条件,而是将连续的最优控制问题离散并参数化,用数值方法对性能指标寻优,其解的收敛半径大,近年来得到广泛应用[4-7]。作为直接法中的一个分支,全局伪谱法发展极为迅速,宗群等[7]将Gauss伪谱法与序列二次规划算法相结合,对存在边值及加速度约束的轨迹优化问题进行了求解。相比于传统的间接法,全局伪谱法收敛速度快,然而在求解非光滑问题时,其收敛速度变慢且无法捕捉状态突变点导致求解精度下降,运用效果不理想[8]。Jiang Zhao等[9]通过分段优化以改善轨迹的非光滑特性,然而在解出最优轨迹之前难以确定要分多少段以及在哪分段。赵吉松等[10-11]基于局部配点法提出自适应网格细化算法,在非光滑区域加密网格以提高求解精度,能够有效控制问题规模,但失去了全局快速收敛的优势。Darby等[12-13]首次提出hp自适应伪谱法并将其应用到最优控制问题上,该方法汲取了全局伪谱法和网格细分法的优点,采用双层优化策略,具有更合理的配点分布,从而提高了算法的优化效率。文献[14-15]将hp自适应伪谱法分别应用于滑翔弹道快速优化问题和再入轨迹优化问题。
本文基于Radau伪谱法提出了一种改进的hp自适应伪谱法,并将该算法应用于高超声速飞行器的最省燃料爬升问题。结果表明,与目前已有的伪谱法相比,改进的hp自适应伪谱法能够以较少的时间代价获得较高精度的解。
1 上升段轨迹优化数学模型
高超声速飞行器上升段轨迹优化问题的数学模型包括动力学模型、推力模型和气动力模型,以及飞行器爬升过程中必须满足的路径约束条件。
1.1 动力学模型
仅考虑飞行器在纵向平面内的质心运动,忽略地球曲率和自转的影响,得到高超声速飞行器上升段的动力学方程如下
(1)
式中,[V,θ,x,y,m]T为系统的状态变量,分别表示飞行器的速度、航迹倾角、航程、飞行高度和质量;P为发动机推力,D为阻力,L为升力,α为攻角,Isp为燃料比冲,μ为地球引力参数,Re为地球半径。
1.2 推力模型
本文采用涡轮冲压发动机与超燃冲压发动机相结合的推力模型。当马赫数小于4时,涡轮冲压发动机提供推力;当马赫数大于4时,超燃冲压发动机提供推力。推力系数和特征冲量的计算公式如下[16]:
1) 推力系数Cp为
(2)
推力P为
(3)
2) 特征冲量Isp为
(4)
式中,h为飞行高度,q为动压,Ae为进气口面积,M为飞行马赫数。
1.3 气动力模型
飞行器飞行过程中受到升力L和阻力D的作用,计算公式如下
(5)
式中,Sref为飞行器参考面积,ρ为大气密度,计算公式为ρ=ρ0e-βh,其中ρ0为海平面大气密度,β为密度系数常数,h为飞行器高度。升力系数CL和阻力系数CD由攻角α和马赫数Ma表示
(6)
式中的系数CLi和CDi基于通用航空飞行器数据[17]。
1.4 约束条件
1.4.1 热流率约束
爬升过程中,为了满足严苛的热防护条件,必须对热流率Qd添加如下约束
(7)
式中,KQ为热流率标准化常数。
1.4.2 动压约束
动压的上限由飞行器执行机构的铰链力矩确定,下限值则是由超燃冲压发动机启动条件所限制。动压q的路径约束可表示为
(8)
1.4.3 过载约束
为保证飞行器的结构不被破坏,需对过载进行约束,即
(9)
式中,g0为海平面重力加速度。
1.4.4 控制量和状态量约束
受机动性能等因素的影响,飞行器在上升段飞行过程中,要求满足一定的控制约束和状态约束。因此建立如下约束条件
(10)
1.4.5 终端约束
飞行器巡航段所需要的初始高度、速度和弹道倾角确定了其爬升段的终端约束,即
(11)
1.5 目标函数
飞行器爬升过程中节省的燃料作为巡航段的燃油增加,可以大大增加巡航段的飞行航程。据此,选取上升段燃料最省为优化目标,即
(12)
1.6 多区间轨迹优化问题描述
基于高超声速飞行器的动力学模型,最省燃料轨迹优化问题的本质为寻找最优控制量α使得目标函数J最小,同时满足多种约束条件((7)~(11)式)。为表述方便,将该问题描述为一般形式的Bolza型最优控制问题:定义状态变量x=[h,V,θ,m]T、控制变量u=α,使代价函数最小化
(13)
约束条件为
(14)
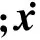
多区间最优控制问题是指将上述Bolza型问题的时间区间[t0,tf]划分为K个子区间,用t0 (15) 将时间区间t∈[tk-1,tk]变换为τ=[-1,1]。 在RPM中,连续Bolza问题的状态变量近似为 (16) (17) (18) (19) (20) 3.1 误差评估准则 在数值求解过程中,若使数值方法的解能够精确地近似原问题的确切解,则需要在任意点处满足微分-代数约束方程。因此,以微分-代数约束方程在配点间的满足程度作为解的近似误差评估准则。 (21) (22) (23) (24) 3.2 多项式阶数的估计 (25) 为保证求得的配点数为整数,对(25)式右边项向上取整,即 (26) 3.3 hp自适应迭代策略 (27) 每个区间内的配点数均设为配点数初始值Nmin。 可以看出,本文所提出的hp迭代策略优先使用p法来提高精度,只有当配点数超过所设定的上限值时才进行区间划分,划分后每个区间内继续采用p法,以此规律不断迭代直到满足解的精度要求。 基于以上的迭代策略,hp自适应算法流程总结如下: ①初始化。令迭代次数M=0,设定区间的初始划分以及区间内配点数上下限Nmin,Nmax; ②将最优控制问题离散化,转化为NLP问题进行求解,并按照3.1节内容计算解的相对最大误差emax; ③若所有区间的emax均小于ε或M>Mmax,停止迭代;否则,继续④; ④在emax>ε的区间内采用3.3节的自适应策略更新网格,直到所有的网格完成更新; ⑤令M=M+1,转向步骤②进行下一次迭代。 本文以某高超声速飞行器为例,飞行器初始质量为3 600 kg,气动参考面积为0.6 m2,给定初始高度y0=17 km,初始速度v0=1 100 m/s,初始弹道倾角θ0=4°,终端高度yf=27 km,终端速度vf=1 870 m/s,终端航迹倾角θf=0°。爬升过程中状态变量、控制变量和路径约束的边界限制如下 表1 约束边界设置 优化计算过程中软件环境为:Windows7 32位操作系统和MATLAB R2013a;硬件环境为:Intel Core i5-2450处理器,4G内存。在精度要求为10-5时,求得的爬升段最小燃料消耗为165.56 kg,整个计算过程用时7.069 8 s,优化结果如图1~图4中a)图的圆点所示。 为验证解的最优性,将最优控制量通过三次样条插值代入到动力学方程中,求得飞行器的实际飞行状态,计算结果图1~图4中a)图的实线所示。离散点处的状态误差如图中星型线所示。图中可以看出两者的相对误差在10-4~10-6之间,解的最优性得到验证。 图1 高度及高度误差曲线 图2 速度及速度误差曲线 图3 航迹倾角及航迹角误差曲线 图4 质量及质量误差曲线 在精度要求为ε的情况下,采用3种不同的伪谱方法对同一航迹优化问题进行求解,优化结果如表2所示。 表2 不同伪谱法的优化比较 表中,p代表全局Radau伪谱法,h代表分段定阶Radau伪谱法,hp代表改进的hp自适应Radau伪谱法。分别表示初始子区间个数和区间内的初始配点数。K0、N0分别表示优化完成时的最大微分-代数约束的误差、计算时间区间个数、整个时间区间的配点总数、迭代次数以及目标函数。需要注意的是在采用全局伪谱法优化时,由于求解问题的不光滑性,精度要求较高时,过多的配点导致优化时间过长,无法得到优化结果。 分析表中数据,我们可以得出如下结论:①精度要求较低时,3种方法均可以优化出结果,且在优化速度和配点总数上无明显差异;②的精度要求下,hp伪谱法逐渐地显现出其优势,不论是优化速度还是配点总数均优于其他2种方法;③随着精度要求的提高,p方法仅通过增加配点数无法得到最优解,而h方法和hp方法成功地克服了不光滑带来的问题,得到最优解。两者相对而言,hp伪谱法在配点总数,子区间划分和优化速度上均优于h方法。 图5 不同伪谱法的配点分布 图5给出了10-3精度下不同伪谱法的配点分布(图中纵坐标无实际物理意义,仅为图示方便,直线上点的横坐标分别表示p伪谱法、h伪谱法和hp伪谱法的配点位置),从图中可以看出:①p方法为全局伪谱法,配点分布具有两端密、中间疏的特点;②h方法通过细化区间来提高精度,每个区间内配点相同,图中可以看出区间的划分;③hp方法不具备统一的配点分布标准,相比于h方法,区间划分较少。 本文中所采用的hp自适应策略为:设定区间配点数上限,当配点数未达到上限时,通过增加区间内配点数(p法)提高精度,当配点数达到上限仍未满足求解精度时,再利用细化时间区间(h法)来提高精度。文献[12]提出另一种自适应策略:通过比较相对曲率rk与曲率阈值rmax的大小关系来决定采取细分时间区间(h法)还是增加区间内的配点数(p法)来提高算法精度。表3为这两种细化策略在不同的精度要求下的优化结果比较,其中hp1表示本文细化策略,hp2为文献[12]中细化策略。 从表3中可以看出,精度要求较低时,hp2方法所需的配点总数小于hp1方法,计算效率也高于hp1;精度要求提高到10-5时,hp2方法逐渐失去了优势;精度为10-6时,hp1方法在计算效率上明显优于hp2方法。分析其可能的原因,文献[12]中hp伪谱法在初始迭代中,NLP问题的解与原问题的解存在较大的误差,此时根据曲率进行分段可能导致分段过多且分段点不准确,且这种情况随着精度要求的提高表现得更为突出,而本文中所采用的hp伪谱法优先采用p法来提高精度,在一定程度上可以消除该问题对求解效率的影响。 表3 不同hp自适应策略的优化对比 本文提出了一种基于hp自适应Radau伪谱法的hp自适应网格算法,并将其应用于高超声速飞行器上升段的轨迹优化问题。仿真结果表明:①与全局伪谱法和固定阶伪谱法相比,hp伪谱法充分结合了p法的快速收敛性和p法的计算稀疏性,具有更合理的配点分布,能够以较少的时间代价获得更高精度的解;②与以曲率为迭代判据的hp伪谱法相比,本文所提出的伪谱法优先采用p方法,在一定程度上能够避免分段过多且不准确的问题,更适合求解高精度的最优控制问题,具有一定的工程应用价值。 [1] Betts J T. Survey of Numerical Methods for Trajectory Optimization[J]. Journal of Guidance Control And Dynamics, 1998, 21: 193-207 [2] 雍恩米,陈磊,唐国金.飞行器轨迹优化数值方法综述[J]. 宇航学报,2008(2):397-406 Yong Enmi, Chen Lei, Tang Guojin. A Survey of Numerical Methods for Trajectory Optimization of Spacecraft[J]. Journal of Astronautics, 2008(2): 397-406 (in Chinese) [3] 黄长强,国海峰,丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J]. 宇航学报, 2014(4):369-379 Huang Changqiang, Guo Haifeng, Ding Dali. A Survey of Trajectory Optimization and Guidance for Hypersonic Gliding Vehicle[J]. Journal of Astronautics, 2014(4): 369-379 (in Chinese) [4] Ma L, Shao Z J, Chen W F, et al. Three-Dimensional Trajectory Optimization for Lunar Ascent Using Gauss Pseudospectral Method[R]. AIAA-2016-1372 [5] 白瑞光. 基于Gauss伪谱法的多UAV协同航迹规划[J]. 宇航学报,2014(9):1022-1029 Bai Ruiguang. Multiple UAV Cooperative Trajectory Planning Based on Gauss Pseudospectral Method[J]. Journal of Astronautics, 2014(9):1022-1029 (in Chinese) [6] 彭祺擘,李海阳,沈红新. 基于高斯-伪谱法的月球定点着陆轨道快速优化设计[J]. 宇航学报, 2010, 31(4): 1012-1016 Peng Qibo, Li Haiyang, Shen Hongxin. Rapid Lunar Exact-Landing Trajectory Optimization via Guass Pseudospectral Method[J]. Journal of Astronautics, 2010, 31(4): 1012-1016 (in Chinese) [7] 宗群,田栢苓,窦立谦. 基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J]. 宇航学报,2010(7): 1775-1781 Zong Qun, Tian Bailing, Dou Liqian. Ascent Phase Trajectory Optimization for Near Space Vehicle Based on Gauss Pseudospectral Method[J]. Journal of Astronautics, 2010(7): 1775-1781 (in Chinese) [8] Huntington G T, Rao A V. Comparison of Global and Local Collocation Methods for Optimal Control[J]. Journal of Guidance, Control, and Dynamics, 2008, 31: 432-436 [9] Zhao J, Zhou R. Reentry Trajectory Optimization for Hypersonic Vehicle Satisfying Complex Constraints[J]. Chinese Journal of Aeronautics, 2013, 26: 1544-1553 [10] 赵吉松,谷良贤,佘文学. 配点法和网格细化技术用于非光滑轨迹优化[J]. 宇航学报, 2013(11): 1442-1450 Zhao Jisong, Gu Liangxian, She Wenxue. Application of Local Collocation Method and Mesh Refinement to Non-Smooth Trajectory Optimization[J]. Journal of Astronautics, 2013(11): 1442-1450 [11] 陈琦. 求解非光滑最优控制问题的自适应网格优化[J]. 系统工程与电子技术, 2015,37(6): 1377-1383 Chen Qi. Adaptive Mesh Refinement for Solving Non-Smooth Optimal Control Problem[J]. Systems Engineering and Electronics, 2015, 37(6): 1377-1383 (in Chinese) [12] Arby C L, Hager W W, Rao A V. An hp-Adaptive Pseudospectral Method for Solving Optimal Control Problems[J]. Optimal Control Applications & Methods, 2011, 32: 476-502 [13] Darby C L, Hager W W, Rao A V. Direct Trajectory Optimization Using a Variable Low-Order Adaptive Pseudospectral Method[J]. Journal of Spacecraft and Rockets, 2011, 48: 433-445 [14] 洪蓓,辛万青. hp自适应伪谱法在滑翔弹道快速优化中的应用[J]. 计算机测量与控制, 2012(05): 1283-1286. Hong Bei, Xin Wanqing. Application of hp-Adaptive Pseudospectral Method in Rapid Gliding Trajectory Optimization[J]. Computer Measurement & Control, 2012(05): 1283-1286 (in Chinese) [15] 王海涛. 基于hp自适应Radau伪谱法的再入飞行器轨迹优化[J]. 科学技术与工程, 2015(02): 165-171 Wang Haitao. Track Optimizing for Reentry Vehicle Based on hp-Adaptive Radau Pseudospectral Method[J]. Science Technology and Engineering, 2015(02): 165-171 (in Chinese) [16] Morimoto H. Trajectory Optimization for a Hypersonic Vehicle with Constraint[D]. Atlanta, Georgia Institute of Technology, 1997 [17] Phillips T H. A Common Aero Vehicle(CAV) Model, Description, and Employment Guide[R]. Technical Report, Schafer Corporation for AFRL and AF-SPC, 2003 [18] Bengson D. A Gauss Pseudospectral Transcription for Optimal Control[D]. Colorado, Massachusetts Institute of Technology, 2005 [19] Hou H, Hager W W, Rao A V. Convergence of a Gauss Pseudospectral Transcription for Optimal Control[C]∥2012 AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, 2012 Ascent Phase Trajectory Optimization for Hypersonic Vehicle Based on hp-Adaptive Pseudospectral Method Liu Ruifan, Yu Yunfeng,Yan Binbin (School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China) An improved hp-adaptive pseudospectral method is developed in the present paper for solving hypersonic vehicle trajectory optimization in ascent phase. The method adopts double-layer optimization strategy to adjust both the mesh spacing and the degree of the polynomial on each interval. First, a relative error estimate is derived based on the residual of the differential-algebraic constraints at sample points. The derived relative error estimate is then used to predict the polynomial degree within a mesh interval. If the polynomial degree estimate remains below a maximum allowable degree, the degree of polynomial is increased to degree estimate. Otherwise, the mesh interval is divided into subinterval. Simulation results show the proposed method is more efficient than either h method or p method. non-smooth; ascent phase; hp-adaptive; pseudospectral method; double-layer optimization 2016-04-02 国家自然科学基金(61104195、61503302)与西北工业大学基础研究基金(GKEY1003)资助 刘瑞帆(1995—),女,西北工业大学硕士研究生,主要从事高超声速飞行器制导研究。 V412.4 A 1000-2758(2016)05-0790-082 Radau伪谱法
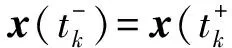
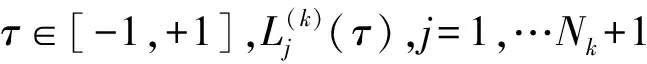
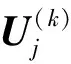
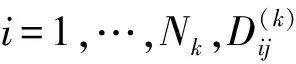
3 改进的hp自适应伪谱法
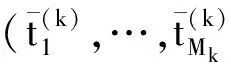
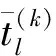
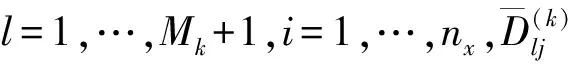
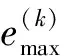
4 仿真分析
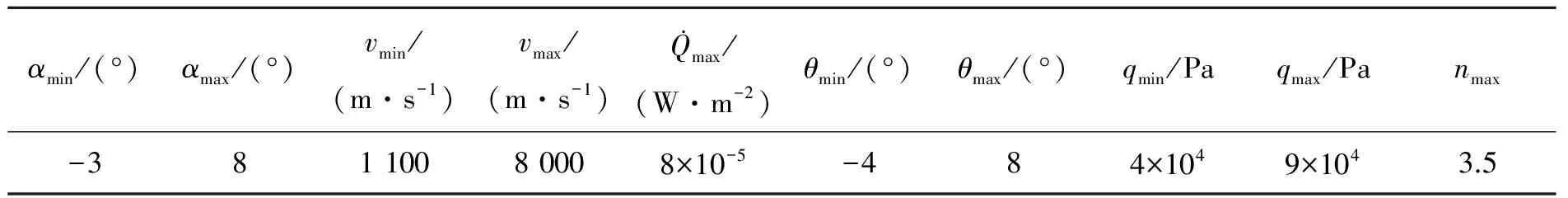
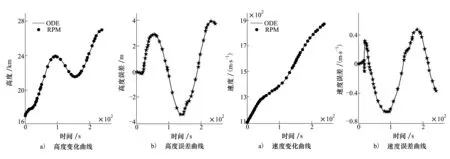
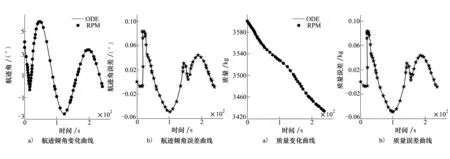

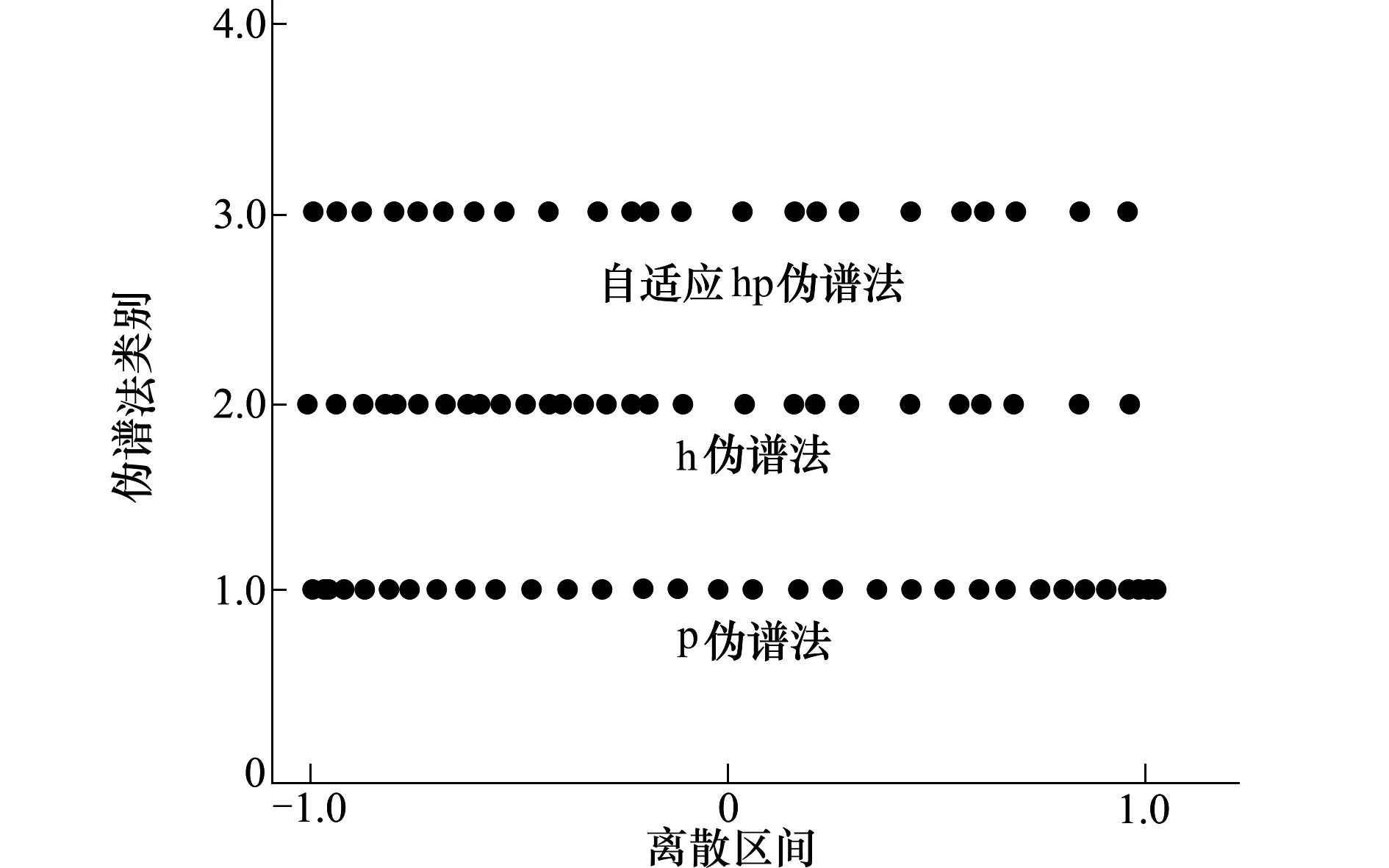
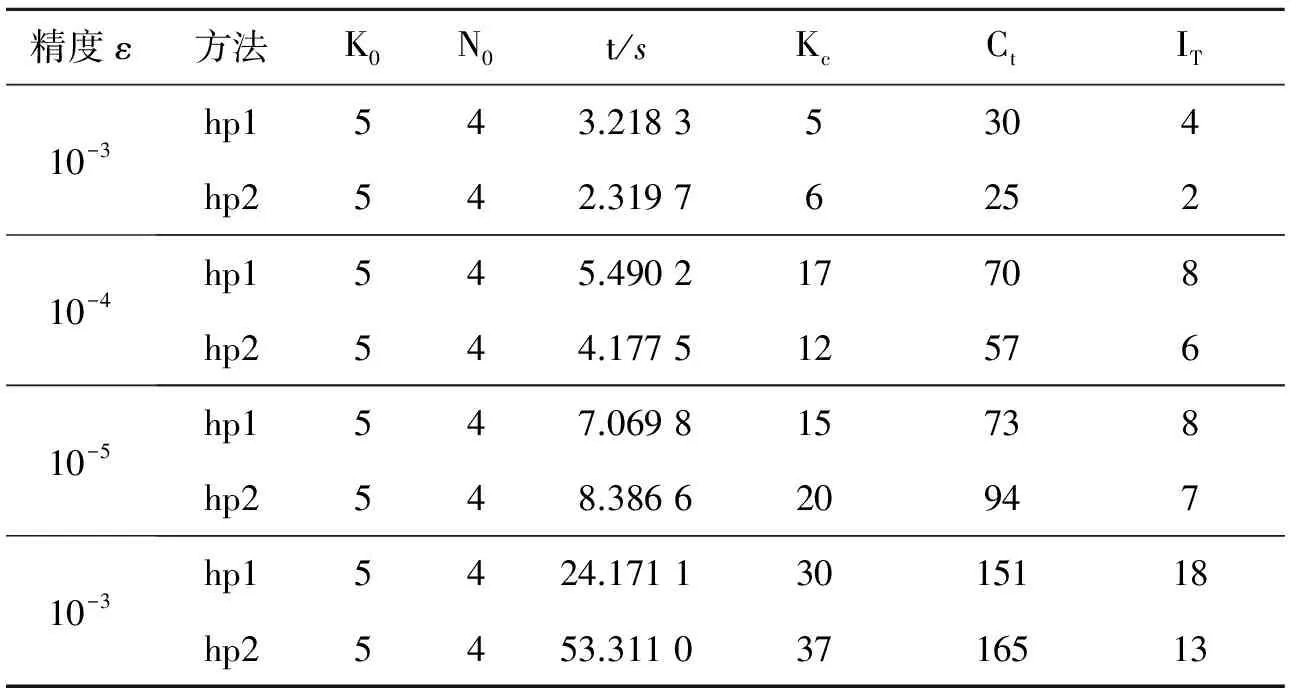
5 结 论
