基于RPLS的造纸废水处理过程软测量建模

杨 浩 莫卫林 熊智新 黄明智 刘鸿斌,*

(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037；2.中山大学水资源与环境系,广东广州，510275)



·废水处理软测量建模·

基于RPLS的造纸废水处理过程软测量建模

杨 浩1莫卫林1熊智新1黄明智2刘鸿斌1,*

(1.南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037；2.中山大学水资源与环境系,广东广州，510275)

偏最小二乘(PLS)软测量预测模型在预测造纸废水处理过程中的出水化学需氧量(CODCr)和固体悬浮物(SS)时,易受过程非线性特性和系统外部干扰等因素的影响而失效。针对以上问题,研究了递归偏最小二乘(RPLS)算法的造纸废水处理过程软测量建模。计算结果表明,采用PLS模型预测出水CODCr时,平均绝对百分比误差(MAPE)、均方根误差(RMSE)和相关系数(R2)分别为5.3832%、4.6878和0.5892；采用RPLS模型预测时，MAPE、RMSE、R2分别为1.3861%、1.8792和0.9221。采用PLS模型预测SS时,MAPE、RMSE和R2分别为2.5962%、0.7412和0.6651；采用RPLS模型时MAPE、RMSE、R2分别为0.6795%、0.2198和0.9627。以上结果表明,RPLS预测模型比PLS预测模型具有更好的预测性能和更高的精度。

递归偏最小二乘；偏最小二乘；软测量建模；造纸废水处理

解决工业过程测量问题一般有两种途径：①应用传感器实现过程参数的直接在线测量。但是许多重要质量变量(如油品黏度、组分等)难以实时测量给化工过程控制和优化带来很大影响[1]。②采用间接测量,利用已经获取的其他参数,通过建立它们之间的数学关系实现对被测变量的估计[2],即软测量技术。

目前造纸废水一般都经过一级物化和二级生化处理[3]。一级物化处理主要用于造纸废水的预处理,能有效地去除固体悬浮物(SS),为后续深度处理废水降低能耗奠定基础；二级生化处理能有效降低废水的CODCr、BOD等[4]。但其处理过程具有复杂性、不确定性、非线性、时变性等特点,难以用精确数学模型描述实际过程,不利于实时控制出水的质量。为了提高废水处理过程的安全状况和出水质量,万金泉等人[5]将自适应模糊神经网络系统用于出水CODCr和SS的预测；胡志华等人[6]提出将ANN算法用于造纸废水处理智能控制系统；李伟奖等人[7- 8]提出分别将模糊神经网络以及遗传算法和BP网络用于造纸废水出水CODCr的预测；许玉格等人[9]提出将Fast-RVM用于废水水质BOD的在线预测。偏最小二乘(Partial Least Squares, PLS)算法具有克服变量间的相关性和噪声干扰等优点,因此,基于PLS算法的软测量技术在工业过程中得到广泛应用。但受实际工况漂移、过程非线性特性和系统外部干扰等因素的影响,PLS预测模型的性能可能会下降,甚至失效[10],需采用在线实时校正技术来维护软测量模型的性能[11]。Helland等人[12]首先提出了递归偏最小二乘(Recursive PartialLeast Squares, RPLS)算法,RPLS模型会在预测过程中不断更新模型的回归系数,以便快速地获取新样品中的有效信息,提高模型的预测能力,扩大模型的使用范围[13]。

本研究采用RPLS算法,建立造纸废水处理过程中进水质量指标(如进水CODCr、SS含量、流量、温度、溶解氧、pH值)和出水质量指标(出水CODCr和SS含量)的预测模型,实现更好地监测制浆造纸废水处理过程的目的。

1 原理和评价指标

1.1 PLS原理

RPLS算法以传统的PLS算法为基础,因此首先介绍PLS算法。PLS是一种能够获得过程数据的方差,同时还能最大化输入矩阵X和输出矩阵Y之间相关性的普遍使用的数据降维和软测量建模工具[14]。

输入矩阵X∈Rn·m,其中包括n组样本和m个测量变量；输出矩阵Y∈Rn·p,包括p个目标变量。输入矩阵X和输出矩阵Y之间的线性关系见式(1)。

Y=XB+E

(1)

式中，E、B分别为残差矩阵和回归系数矩阵。在PLS算法中,输入X、输出Y可表达为式(2)和式(3)。

X=TPT+EX

(2)

Y=UQT+EY

(3)

式(2)中T=[t1,t2…t1]n·l∈Rn·l和式(3)中U=[u1,u2…ul]n·l∈Rn·l分别为X和Y的得分矩阵；P=[p1,p2…pl]m·l∈Rm·l和Q=[q1,q2…ql]p·l∈Rp·l是相应的负荷矩阵；EX∈Rn·m、EY∈Rn·p分别是X、Y的残差阵。l是模型中使用的潜变量个数。

输入和输出矩阵X、Y按式(4)和式(5)迭代分解。

(4)

(5)

式中，t1、u1分别是得分矩阵T、U的第一列,p1、q1为负荷矩阵P、Q的第一列,EX,1、EY,1为输入和输出数据第一次迭代的残差。潜在得分向量t1、u1的线性关系表达见式(6)。

u1=b1t1+r1

(6)

式中，b1是最小化残差r1确定的系数。上述第一组潜在得分向量计算得到后,第二组得分向量可通过式(7)和式(8)分解残差EX,1、EY,1计算。

(7)

(8)

得分向量t1正交于EX,1、EY,1[15]。可通过重复以上步骤l次来求得所有的T、P、U、Q矩阵,B=diag{b1…bl},称为回归系数阵。因此,PLS算法可总结为式(9)。

(9)

式中，W为权重矩阵。当PLS的模型矩阵都求得之后,根据式(1),可由新的输入预测新的输出。PLS模型中的潜变量个数l可用交叉验证法求得[16]。

1.2 RPLS原理

传统的PLS模型运用从历史数据的离线训练过程中求得的模型矩阵T、W、P、Q、B进行预测,因此在处理具有高时变性的动态过程数据时,PLS模型很有可能会失效。针对以上问题,Helland等人首先提出了RPLS回归算法。RPLS模型中,PLS模型会根据新数据的增量积分来定期的更新[16]。

对于RPLS模型,在基于训练数据的基础上求得T、W、P、Q、B矩阵之后,PLS模型会将新的样本数据xt、yt并入一个带有遗忘因子λ(0<λ≤1)的模型来更新，见式(10)和式(11)。

(10)

(11)

式中，λ值越小,新数据的影响就越大,而以前的PLS模型的影响就越小,这样PLS模型就能对新数据具有更快速的适应性。运用具有r(r是Xt的秩)个潜变量的PLS模型和式(10)、式(11)中的增广矩阵,就可以根据新的样本数据xt+1来预测目标变量yt+1。Qin[17]已经证明,在没有遗忘因子的情况下,基于式(10)、式(11)的PLS模型的预测结果和基于式(12)、式(13)的PLS模型是一致的。

(12)

(13)

因为式(12)、式(13)样本的数量通常情况下大于式(10)、式(11)中输入矩阵的秩,所以有新数据加入原有数据库时,RPLS算法比重新校正常规的PLS算法更加有效[16]。

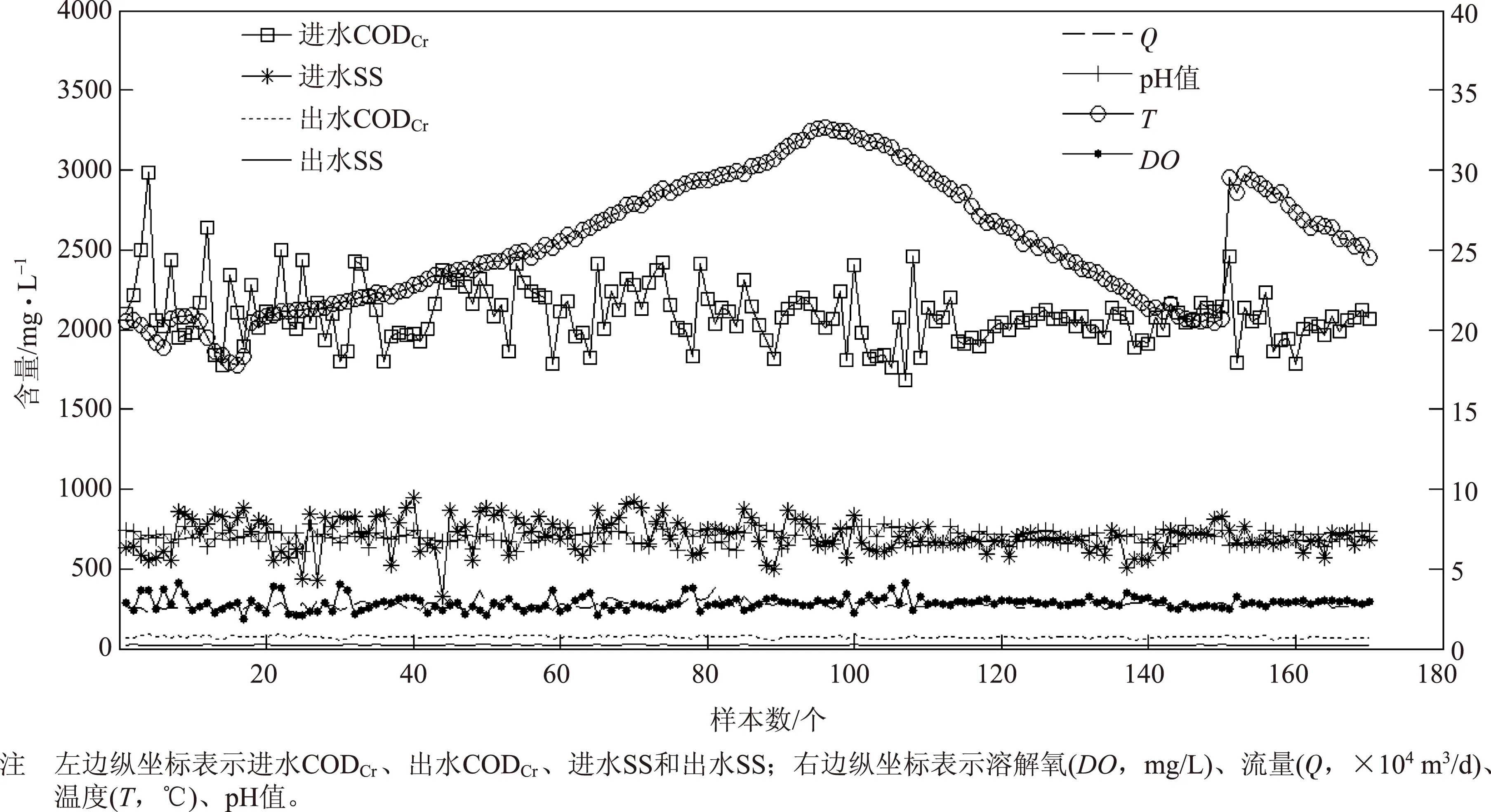
图1 废水处理过程变量

1.3 预测模型的性能评价指标

为了对不同预测模型的预测性能进行准确地分析和评价,引入均方根误差(root mean square error, RMSE)、相关系数(squared correlation coefficient,R2)、平均绝对百分比误差(mean absolute percentage error,MAPE)3个性能指标对RPLS、PLS两种模型的预测性能进行评价。其中R2越大,RMSE和MAPE越小,代表模型性能越好,越精确[13]。

RMSE定义见式(14)。

(14)

式中，ai是测量值,pi是对应的预测值,n是样本的数量。

MAPE定义见式(15)。

(15)

R2定义见式(16)。

(16)

式中，cov(a,p)是a和p之间的协方差。

2 仿真实验与讨论

2.1 仿真软件介绍

本实验建模过程中用到的软件包括了MATLAB2010b和NIRSA数据处理系统。

NIRSA数据处理系统由江苏大学近红外研究室和南京林业大学轻工科学与工程学院自动化研究室共同研制。该系统主要用于近红外光谱数据定性和定量分析,同时也可满足中红外光谱、数据分析、某些多元统计分析和模式识别工作的要求。

2.2 数据的收集与预处理

实验数据来自广东东莞的造纸废水处理厂在2006年3月15日到2006年12月21日期间好氧段废水的监测结果,共计170组。其中120组作为训练数据,50组作为测试数据。图1所示为废水处理过程中每个样本对应的各个变量的具体数值。在国内,工业废水是否符合国家排放标准,出水CODCr含量和出水SS含量是两项重要指标。因此在废水处理过程中,出水CODCr含量和SS含量的监测和控制对于废水处理过程具有重要的意义。

不同变量常常具有不同的单位和不同的变异程度,所以需要消除量纲影响和变量自身变异大小以及数值大小的影响。因此本实验在分析数据之前,先对自变量矩阵X和因变量矩阵Y分别进行式(17)标准化。

(17)

2.3 交叉验证

在建立RPLS和PLS预测模型过程中,潜变量的个数即主成分数是一个很重要的因素。用交叉验证的方法检验每个主成分下样本的预报误差平方和(Predicted Error Sum of Squares,PRESS),选择PRESS值最小或不再变小的主成分数。

在NIRSA数据处理系统中进行交叉验证确定主成分个数。图2表明当主成分的个数为4时,出水CODCr预测模型的PRESS值最小,且当主成分个数增加时,PRESS值不再变小,因此出水CODCr预测模型的主成分个数取4。图3表明当主成分个数为3时,出水SS预测模型的PRESS值最小,所以出水SS预测模型的主成分个数取3。

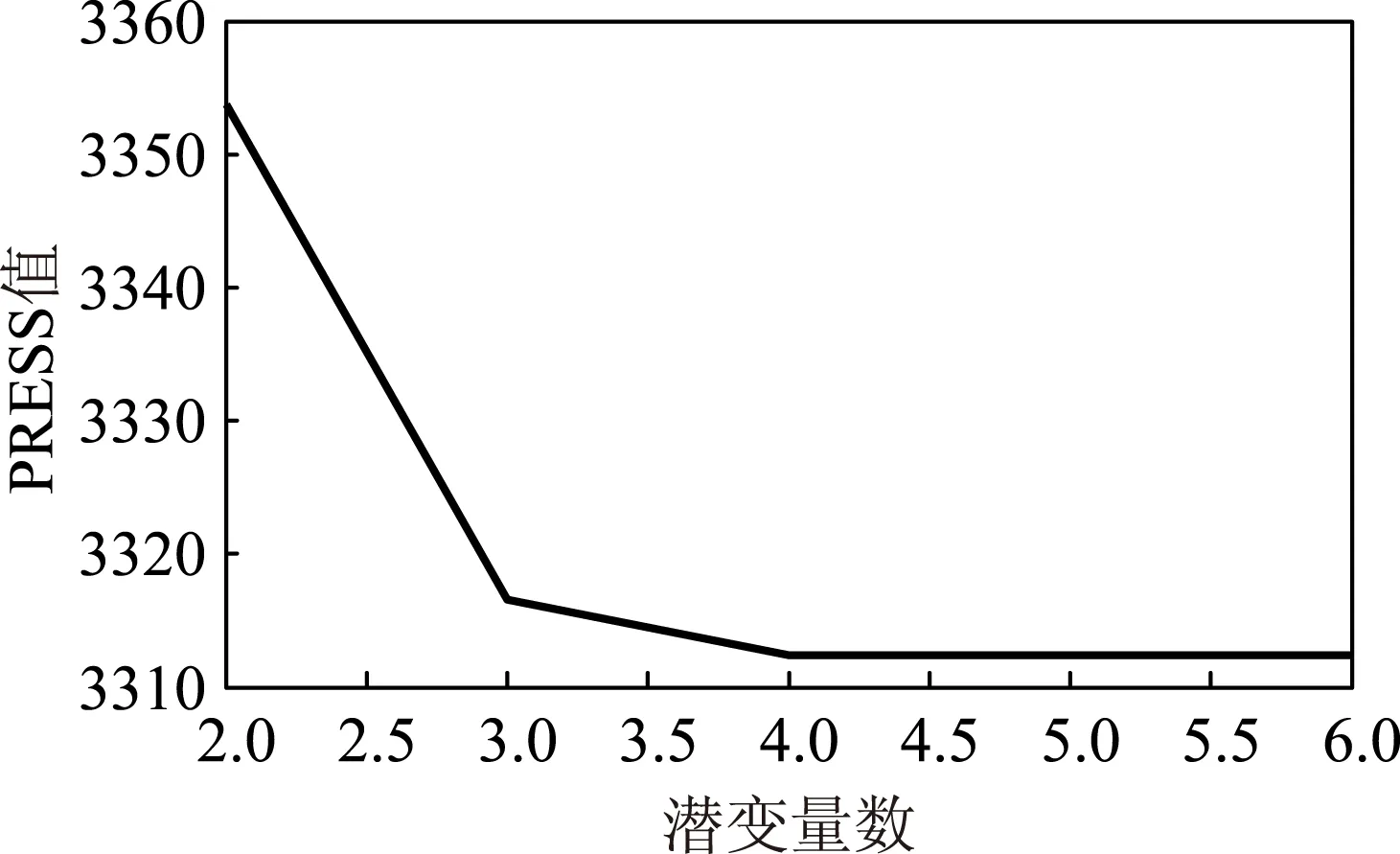
图2 出水CODCr预测模型交叉验证

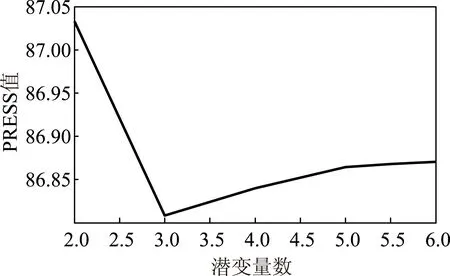
图3 出水SS预测模型交叉验证

2.4 不同方法预测结果比较分析

表1列出了RPLS和PLS模型预测结果的各项性能指标,图4和图5分别为采用两种模型对出水CODCr和SS的预测结果与测量结果的对比。

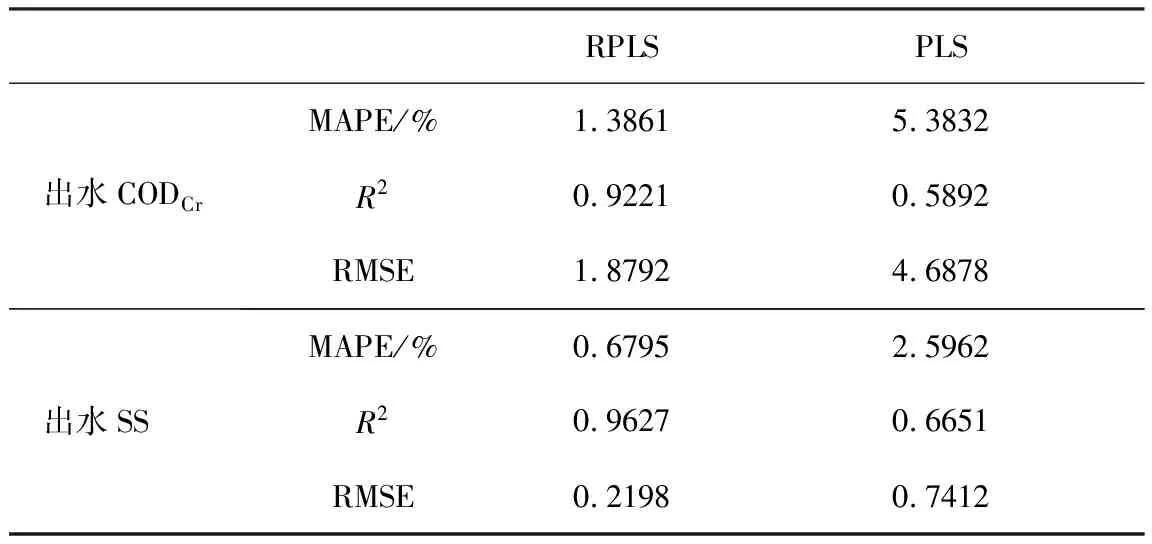
表1 RPLS和PLS预测模型性能指标

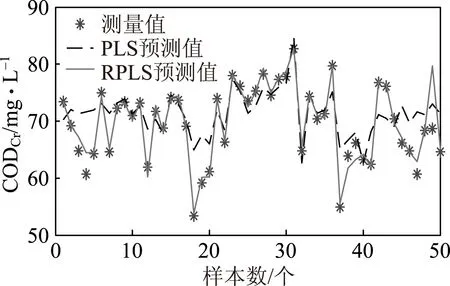
图4 RPLS和PLS模型预测出水CODCr对比

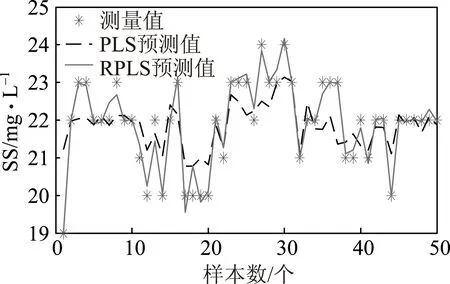
图5 RPLS和PLS模型预测出水SS对比

由表1可以看出,采用RPLS模型预测出水COD和出水SS时,MAPE分别为1.3861%和0.6795%,RMSE分别为1.8792和0.2198,R2分别为0.9221和0.9627。当采用PLS模型预测出水CODCr和出水SS时,MAPE分别为5.3832%和2.5962%,RMSE分别为4.6878和0.7412,R2分别为0.5892和0.6651。由以上结果可知,RPLS模型的RMSE和MAPE均小于PLS模型,R2均大于PLS模型。图4和图5分别为RPLS和PLS模型预测的出水CODCr和出水SS对比。由图4和图5可知,RPLS模型的预测值与测量值相较于PLS模型更加接近,PLS模型在预测3、4、5、7、12、13、14、36、47号样品的出水CODCr以及2、3、7、11、13、29、44号样品的出水SS时,偏差较大,吻合程度较差。由表1中的性能指标和图4、图5中的对比结果可知,RPLS模型具有更好的预测性能和更高的预测精度。

3 结 论

采用递归偏最小二乘(RPLS)和偏最小二乘(PLS)算法对造纸废水处理过程中的出水CODCr和出水SS值进行预测。

(1)与PLS模型的预测结果相比，基于RPLS算法的预测模型对出水CODCr和SS值的预测结果更加接近测量值,表明RPLS算法是一种具有良好预测性能的软测量建模方法。

(2)采用RPLS方法对纸厂废水处理过程所建立的预测模型会不断更新模型参数,有效提高了模型的预测能力,扩大了模型的适用范围。

[1] CAO Pengfei, LUO Xionglin. Modeling of soft sensor for chemical process[J]. CIESC Journal, 2013, 64(3): 788.

曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3): 788.

[2] LIU Bo, WAN Jinquan, HUANG Mingzhi, et al. A PCA-LSSVM model for on-line prediction of the effluent VFA in a anaerobic wastewater treatment system[J]. Acta Scientiae Circumstantiae, 2015, 35(6): 1768.

刘 博, 万金泉, 黄明智, 等. 基于PCA-LSSVM的厌氧废水处理系统出水VFA在线预测模型[J]. 环境科学学报, 2015, 35(6): 1768.

[3] WAN Jin-quan, ZHU Ying-liang, MA Yong-wen, et al.Pilot Study on Advanced Treatment of Papermaking Wastewater by SR-AOPs[J]. China Pulp & Paper, 2015, 34(1): 1.

万金泉, 朱应良, 马邕文, 等. SR-AOPs深度处理制浆造纸废水的研究[J]. 中国造纸, 2015, 34(1): 1.

[4] WANG Chun, PING Qing-wei, ZHANG Jian, et al. Research and Application of New Technologies for Pulp and Paper Wastewater Treatment[J]. China Pulp & Paper, 2015, 34(2): 61.

王 春, 平清伟, 张 健, 等. 纸浆造纸废水处理新技术[J]. 中国造纸, 2015, 34(2): 61.

[5] Wan Jinquan, Huang Mingzhi, Ma Yongwen, et al. Prediction of effluent quality of a paper mill wastewater treatment using an adaptive network-based fuzzy inference system[J]. Applied Soft Computing, 2011, 11(3): 3238.

[6] HU Zhi-hua, WAN Jin-quan, MA Yong-wen, et al. An Intelligent Control System Based on ANN[J]. Environmental Science and Technology, 2007, 30(3): 58.

胡志华, 万金泉, 马邕文, 等. 基于ANN的造纸废水处理智能控制系统研究[J]. 环境科学与技术, 2007, 30(3): 58.

[7] LI Weijiang, MA Yongwen. Study on the Prediction of Papermaking Wastewater Treatment Process with Fuzzy Neural Network[J]. Paper Science & Technology, 2010, 29(1): 80.

李伟奖, 马邕文. 基于模糊神经网络的造纸废水处理预测研究[J]. 造纸科学与技术, 2010, 29(1): 80.

[8] LI Wei-jiang, MA Yong-wen. Predicting the Papermaking Wastewater Treatment Process Based on Genetic Algorithm and Neural Network.[J]. Transactions of China Pulp and paper, 2010, 25(1): 67.

李伟奖, 马邕文. 基于遗传算法和BP网络的造纸废水处理预测研究[J]. 中国造纸学报, 2010, 25(1): 67.

[9] XU Yuge, LIU Li, CAO Tao. On-line soft measuring model based on Fast-RVM[J]. CIESC Journal, 2015, 66(11): 4540.

许玉格, 刘 莉, 曹 涛. 基于Fast-RVM的在线软测量预测模型[J]. 化工学报, 2015, 66(11): 4540.

[10] XU Ouguan, CHEN Xianghua, FU Yongfeng, et al. Recursive PLS modeling based on model performance assessment and its application[J]. CIESC Journal, 2014, 65(12): 4875.

徐欧官, 陈祥华, 傅永峰, 等. 基于模型性能评估的递推PLS建模及应用[J]. 化工学报, 2014, 65(12): 4875.

[11] Kadlec P, Grbi R, Gabrys B, et al. Review of adaptation mechanisms for data-driven soft sensors[J]. Computers & Chemical Engineering, 2011, 35: 1.

[12] Helland K, Berntsen H E, Borgen O S, et al. Recursive algorithm for partial least squares regression[J]. Chemometirics & Intelligent Laboratory Systems,1992,14: 129.

[13] JIA Sheng-yao, YANG Xiang-long, LI Guang, et al. Quantitatively Determination of Available Phosphorus and Available Potassium in Soil by Near Infrared Spectroscopy Combining with Recursive Partial Least Squares[J]. Spectroscopy and Spectral Analysis, 2015, 35(9): 2516.

贾生尧, 杨祥龙, 李 光, 等. 近红外光谱技术结合递归偏最小二乘算法对土壤速效磷与速效钾含量测定研究[J]. 光谱学与光谱分析, 2015, 35(9): 2516.

[14] Liu Hongbin, Kang OnYu, Kim MinJeong, et al. Sustainable monitoring of indoor air pollutants in an underground subway environment using self-validating soft sensors[J]. Indoor and Built Environment, 2012, 22(1): 94.

[15] Tiago Matias,Francisco Souza, Rui Araujo, et al. On-line sequential extreme learning machine based on recursive partial least squares[J]. Journal of Process Control, 2015, 27: 15.

[16] Wangdong Ni, Soon Keat Tan, Wun Jern Ng, et al.Localized, adaptive recursive partial least squares regression for dynamic system modeling[J]. Industrial & Engineering Chemistry Research, 2012, 51(23): 8025.

[17] Qin S J. Recursive PLS algorithms for adaptive data modeling[J]. Computers & Chemical Engineering, 1998, 22(4/5): 503.

(责任编辑：董凤霞)

Soft Sensor Modeling of Papermaking Effluent Treatment Processes Using RPLS

YANG Hao1MO Wei-lin1XIONG Zhi-xin1HUANG Ming-zhi2LIU Hong-bin1,*

(1. Jiangsu Provincial Key Lab of Pulp and Paper Science and Technology, Nanjing Forestry University,Nanjing,JiangsuProvince, 210037; 2.DepartmentofWaterResourcesandEnvironment,SunYat-SenUniversity,Guangzhou,GuangdongProvince, 510275)(*E-mail: hongbinliu@njfu.edu.cn)

Soft sensor modeling methods based on partial least squares (PLS) and recursive PLS (RPLS)were used to predict effluent chemical oxygen demand(CODCr) and effluent suspended solids(SS) in a papermaking wastewater treatment process. PLS is unsuitable for the systems with non-linear characteristics and external disturbances. The results showed that the mean absolute percentage error(MAPE),root mean square error(RMSE), and squared correlation coefficient(R2) for CODCrusing PLS were 5.3832%, 4.6878, and 0.5892, respectively, and they were 1.3861%, 1.8792, and 0.9221, respectively using RPLS. In terms of SS, the MAPE, RMSE, andR2were 2.5962%,0.7412, and 0.6651, respectively when using PLS, and the three indices using RPLS were 0.6795%, 0.2198, and 0.9627, respectively. These results indicated that the RPLS model had better prediction performance and higher accuracy compared to the PLS model.

recursive partial least squares; partial least squares; soft sensor modeling; papermaking effluent treatment

杨 浩先生,在读硕士研究生；研究方向：制浆造纸过程控制与信息智能处理。

2016- 05- 05(修改稿)

南京林业大学高层次人才科研启动基金(No.16310-5996)；江苏省制浆造纸科学与技术重点实验室开放基金项目(201010)；江苏高校优势学科建设工程资助项目(PAPD)。

TP27

A

10.11980/j.issn.0254- 508X.2016.10.007

*通信作者：刘鸿斌先生,E-mail:hongbinliu@njfu.edu.cn。