地效飞机着水冲击载荷理论计算与试验
2016-11-18褚林塘吴彬王明振孙丰
褚林塘, 吴彬, 王明振, 孙丰
1.中航通用飞机有限责任公司, 珠海 519030 2.高速水动力航空科技重点实验室, 荆门 448035 3.中航工业特种飞行器研究所, 荆门 448035
地效飞机着水冲击载荷理论计算与试验
褚林塘1,2,*, 吴彬2,3, 王明振2,3, 孙丰2,3
1.中航通用飞机有限责任公司, 珠海 519030 2.高速水动力航空科技重点实验室, 荆门 448035 3.中航工业特种飞行器研究所, 荆门 448035
针对地效(WIG)飞机遭受冲击最为严重的状态——对称断阶着水情况,对影响冲击的各个因素进行了比较分析,在作了一些基本假设后,采用船舶运动中常用的切片理论思想,结合Von Karman水动力学分析的动量概念及Wagner的附连水质量公式,提出了一种理论计算方法。同时,还将理论计算结果与试验结果进行了比对分析。计算值与试验值的比较结果说明,理论计算在较大程度上是可信的,可作为结构设计外载荷确定的参考。
地效飞机; 水动冲击载荷; 对称断阶; 切片理论; 附连水质量
当前,中国地效飞机的研究总体上正处于从原理试验样机阶段向实用化产品发展、从小吨位向大装载量发展的时期,而随着地效飞机的实用化、大型化,水动力问题的研究日趋迫切,特别是其中的冲击问题,一是如何准确预报冲击载荷,二是如何有效降低冲击载荷对飞机船体的破坏作用。前者可以通过理论预报和试验验证等方法来解决,后者则要通过采取结构优化设计或辅助装置来解决。
以往的地效飞机载荷研究中[1-8],除俄罗斯外,基本都限于小型试验机,冲击问题并不突出,水动力设计基本沿用水上飞机的一套方法,其船体线型与水上飞机基本类似。在结构设计上,也基本参考水上飞机规范中的水载荷确定方法。
地效飞机的着水载荷,与水上飞机有类似之处,在本质上都可以归结到Von Karman[9]和Wagner[10]对于楔形体入水的冲击和滑行现象所做的研究。Von Karman将动量的概念用于撞水力学分析,认为在任一时刻入水楔形体和附连水质量总的动量守恒。Wagner进一步考虑了水面升高对附连水质量的影响。在此基础上,各国科技工作者进行了大量的研究,提出了许多有价值的计算方法,其中Monaghan 和 Crewe[11]提出的理论获得了普遍认可,英国、美国及中国规范中的水上飞机主断阶撞击载荷这一条均建立在此理论及大量试验数据和分析基础之上。此理论假设水上飞机着水后不旋转(即固定纵倾)、机翼气动升力等于着水重力、船身舭部不浸水,但后两项假设与实际情况是有所出入的。
地效飞机具有多种航态,包括水上起飞滑跑、空中飞行、水上降落和水面航行等。一般认为,在水上降落时,地效飞机承受着最为严重的水动冲击载荷。对于船体而言,对称断阶着水载荷占主导地位,情况最为严重。所以本文重点针对地效飞机断阶对称着水这一情况,从理论上探求着水冲击载荷的预报方法,然后用模型试验结果校核这种方法的可信度。
1 着水运动方程及载荷的确定
1.1 基本假设
影响地效飞机断阶着水冲击载荷的因素很多,主要有:地效飞机的质量及其分布;船底形状;与水面接触时的飞机纵倾角、水平速度及垂直速度等运动参数;水面的风及波浪的大小和方向等。
根据地效飞机的实际着水情况,分析不同因素的影响程度大小,在不失必要的准确性的情况下,为简便分析,本文作以下几点假设:
1) 机体视为刚体。
2) 在撞击过程中,惯性力居支配地位,浮力、黏性力可以忽略不计。
3) 从着水瞬时到最大过载的时间很短,平行于龙骨方向的速度变化不大,可视为常数。
4) 根据Miller的研究[12],飞机着水后旋转(即自由纵倾)对着水载荷的影响不是太大,为简便分析,假定飞机着水后不旋转,即固定纵倾。
5) Sim和Schnitzer的研究[13]表明,机翼升力不等于着水重力时,冲击载荷变化较大。水上飞机规范中假设机翼升力等于2/3着水重力进行简化处理,地效飞机由于动力增升产生气垫的作用,近水面时升力会更大,着水运动要缓和得多。本文对气垫的作用规律不作讨论,从工程角度,可以把它归结到对机翼升力的影响,简单地,可以认为机翼升力L与着水重力W之比为一常数p,即p=L/W,p的取值范围应在2/3~1之间,具体取值可根据实际情况和试验数据确定。
6) 由于船体舭部浸水后的附连水质量与舭部不浸水时的情况有所不同,本文考虑舭部浸水时的情况。
1.2 坐标系
如图1所示,建立坐标系如下:
1) 定坐标系Oxy,x轴重合于未受扰动的自由水面,x轴方向与地效翼的水平运动方向相同,y轴方向铅垂向下。
2) 动坐标系O1sζ固结于龙骨下缘,s轴平行于龙骨,艏部方向为正,ζ轴垂直于龙骨,向上为正。
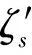
1.3 基本运动方程
地效飞机的受力如图2所示,其着水的运动为
(1)
(2)
(3)

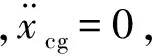
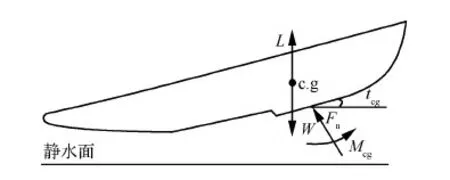
图2 着水受力示意图Fig.2 Sketch map of water load
Fncosτcg,要求解的方程即为
(4)
则此问题的关键在于如何求解撞击力Fn。
1.4 撞击力Fn的确定
根据切片理论(Strip Theory),即沿着龙骨将浸湿船体切成许多微段ds,把每一微段ds看成二元楔形体在水中运动,整个船体的水动力为楔形体微段的水动力之和,于是有

(5)
式中:φ(λ′)为三元流动修正项;dFn为作用于船体ds微段上的水动力。
根据动量定理
(6)
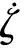
则可得
(7)
在进一步分析Fn之前,先讨论三元修正项φ(λ′)和二元附连水质量mw。
1) 三元修正项φ(λ′)
根据Willelm[14]的平板试验研究,三元流动的修正经验公式为
(8)
式中:λ′为考虑水面上升影响的龙骨浸湿长宽比。
根据Wagner[10]的研究和大量的试验数据,得到有效浸湿长宽比λ′和平均浸湿长宽比λ的关系为
(9)
式中:系数c=0.4;
(10)
其中:f(β)=π/2β-1,β为船体底部斜升角;b为舭部宽度。
2) 二元楔形体的附连水质量mw
船体舭部不浸水和舭部浸水的附连水质量是不同的。在以前的分析研究中,都是假定舭部不浸水,这与实际情况不符。下面分别就舭部浸水和不浸水的情况加以讨论。
① 舭部浸水前的mw
在文献[15-16]中,考虑水面上升影响的二元楔形体的附连水质量为

(11)
在舭部

则舭部浸湿瞬时的附连水质量为

(12)
采用舭部浸湿瞬时的附连水质量mw加上浸湿后的附连水增量Δmw来表示舭部浸湿后的附连水质量,附连水质量增量Δmw可由Bobyleff理论求得。

(13)
式中:B为船体底部斜升角β的函数,其随β的变化值已画成图表,可参见文献[17],近似表达式为
B=0.88cosβ
(14)
又根据动量定理,有

(15)


(16)
通过积分式(16)即可求得舭部浸湿后的附连水质量增量Δmw,则舭部浸湿后的附连水质量为
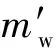
(17)

(18)

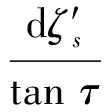
(19)
将式(18)和式(19)代入式(7),得
(20)
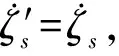
(21)
同时,由图1可知:
(22a)
(22b)

(22c)
(23)
令
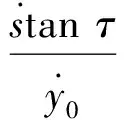
(24)
将式(23)和式(24)代入式(4),得
(p-1)W
(25)
1.5 波浪上着水降落时运动参数的处理
实际上,地效飞机的航行区域是在海上,它将不可避免地遭受到波浪的冲击,与静水中相比,其所受冲击载荷要大的多。由于波浪的随机性,船体的运动参数如纵倾角、航迹角、下沉速度也将是随机变化的,着水时船体与波浪的冲击载荷是随机值。在目前的条件下,不可能精确描述船体与波浪发生冲击的初始条件与边界条件,以及每个瞬时船体相对于波浪的位置。为准确预报地效飞机在波浪上着降时的冲击载荷,就需要进行大量的数学统计,这就使问题显得比较复杂。从工程应用角度,关心的则是最大过载,即对结构强度而言最为危险的情况,这样只需处理波浪波倾角最大时船体着水降落的情况。
假定此时仍是船体主断阶着水,考虑船体与波浪之间的相对运动,参考运动着的波浪确定初始参数,即可以把静水中的处理方法移用到波浪中去。作为一种近似,把波浪的运动简化为某个相当于倾斜水面的平面移动,移动速度取为波速。该倾斜平面相当于静水面有一倾角,按照上述考虑,取为波面的最大波倾角。设地效飞机的初始纵倾角为τ,初始航迹角为γ0,水平速度为VX,垂向速度为VY,则相对于倾角为θ的波平面,各有效初始参数为
τe=τ-θ
(26)
VXe=VX±VW
(27)
γe=θ+arctan(VY/VXe)
(28)
VYe=VYcosθ+(VX±VW)sinθ
(29)
式中:τe为有效纵倾角;VXe为有效水平速度;γe为有效航迹角;VYe为有效垂向速度。
有关的波浪要素为
θ=arctan(πH/λ)
(30)

(31)
式中:Vw为波速;H为波高;λ为波长。
于是,问题转化为地效飞机以有效纵倾角τe、有效航迹角γe、有效水平速度VXe和有效垂向速度VYe对斜面的静水冲击问题。
2 计算与分析
2.1 典型理论计算结果
利用第1节所述理论计算方法,本文对25 kg地效飞机模型的着水冲击进行了计算,其有关参数如下:总质量25 kg,总长2.8 m,总宽0.28 m,吃水0.11 m,前体长1.295 m,后体长0.505 m,断阶高度为0.068 m,断阶前斜升角为15°,断阶后斜升角为20°,后缘角为6°。
在设计降落速度VX≈10 m/s的情况下,当初始纵倾角τ=4.0°、初始航迹角γ0=4.0°时,计算了其典型的着水运动及载荷,常数p保守取值为2/3,结果如图3~图5所示,图中a、Y/b和VY/VY0分别表示着水冲击加速度、浸湿深度及下沉速度的无因次量。
图3~图5给出了应用本文计算方法和文献[11]中计算方法所得的计算结果,可以看出升力的减小和舭线浸水会导致相同时刻加速度减小、浸水深度增加、下落速度变大,文献[11]中的升力假设和舭线不浸水假设使得过载峰值被高估了约10%,浸水深度更早达到最大。
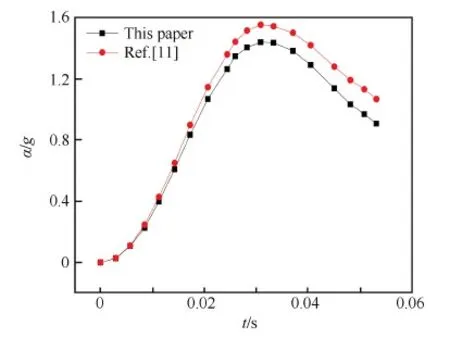
图3 着水冲击加速度变化曲线Fig.3 Changing curves of impact acceleration of landing on water

图4 船体浸湿深度变化曲线Fig.4 Changing curves of depth of water-entry of ship body
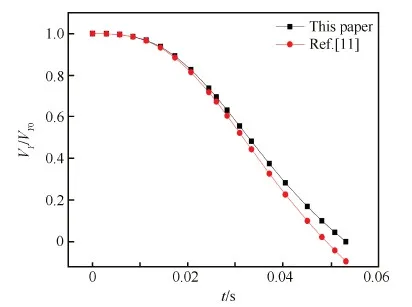
图5 飞机下沉速度变化曲线Fig.5 Changing curves of vertical velocity of aircraft
由图3~图5可以看出,冲击时间较短,本文计算方法所得的冲击加速度在0.03 s左右很快达到最大值(约为1.5g),然后迅速下降,下沉速度也在0.05 s左右急剧减小为零,而浸湿深度也很快趋于稳定。当然,这是理论计算结果的理想状态,反映了着水冲击的基本过程,实际着水冲击则要复杂的多,有时甚至可能出现船体在水面多次弹跳冲击的现象。
2.2 理论计算与试验结果的比较
基于国内外关于地效飞机冲击载荷方面的试验资料非常有限,为校核理论计算冲击载荷的可信度,本文采用某型水上飞机的单船身模型水池着水冲击试验的结果,与理论计算结果进行了对比分析(见表1和表2)。该项单船身模型水池着水冲击试验,是在拖曳水池进行的,试验主要测试飞机在不同高度下以不同水平速度、不同着水纵倾角入水时船身受到的冲击载荷,进而分析研究飞机水平速度、垂向速度、纵倾角等运动参数对冲击性能的影响。
从表1和表2可以看出,理论计算值与模型水池试验值的结果比较吻合,静水中的计算值与试验值误差相对较小,而波浪中的数据误差要大一些。分析波浪中数据误差偏大的原因,主要是因为试验中船体与波浪的遭遇位置具有很大的随机性。本文计算值普遍较文献[11]计算值小,误差更小一些,文献[11]计算值对于结构强度校核来说偏于保守。

表1 静水计算值与试验值的比较Table 1 Comparison of calculated and test values in calm water

表2 波浪水面计算值与试验值比较(波长6.1 m,波高0.21 m)Table 2 Comparison of calculated and test values in wave (wave length 6.1 m, wave height 0.21 m)
3 结 论
本文针对地效飞机起飞和降落时的运动和载荷,基于其中冲击最为严重的状态——对称断阶着水情况,提出了一套着水载荷理论计算方法,并给出了典型计算结果。同时,还利用模型水池试验结果,与理论计算值进行了比较。
1) 在目前地效飞机模型试验数据积累较少、试验方法还有待进一步完善的情况下,该理论计算方法是研究地效飞机冲击问题的一个有效途径。
2) 本文提出的地效飞机着水载荷理论计算方法具有较好的可信度,可作为地效飞机结构设计过程中确定外载荷时的重要参考。
就本文提出的理论计算方法而言,尚存在着冲击运动方程偏于简化、附加质量处理经验性偏强等问题,在今后的工作中有待进一步改进。
[1] 孙俊, 石岩峰, 凤蕴, 等. 20米地效翼船试验体系研究[J]. 船舶工程, 2008, 30(3): 76-79.
SUN J, SHI Y F, FENG Y, et al. Research of the test system of the 20 m wing-in-ground craft[J]. Ship Engineering, 2008, 30(3):76-79 (in Chinese).
[2] BUTER E A. Wing-in-ground-effect vehicles[J]. Naval Engineers Journal, 1985(2): 254-258.
[3] ROZHDESTVENSKY K V. Ekranoplan—Flying ships of the next century[C]//Second International Conference on Ekranoplans, 1995: 47-70.
[4] KIRRILLOVIKH V N. Russian Ekranoplans[C]//Second International Conference on Ekranoplans, 1995: 71-117.
[5] MALYSHEV M I. Experience of using Ekranoplans in Russia navy[C]//Second International Conference on Ekranoplans, 1995: 233-244.
[6] 安东茂典. 米国DTNSRDCのPAR-WIG设计の基本思想[J]. 日本航空宇宙学会杂志, 1991, 39(448): 14-22.
ANTON S. The fundamental theory of the design of America PAR-WIG DTNSRDC[J]. Journal of the Aerospace Society of Japan, 1991, 39(448): 14-22 (in Japanese).
[7] 安东茂典, 加藤三千代. PAR-WIGの离水性能予测法[J]. 日本航空宇宙学会杂志, 1991, 39(455): 38-46.
ANTON S, KATO M. The prediction method of PAR-WIG on take-off performance[J]. Journal of the Aerospace Society of Japan, 1991, 39(455): 38-46 (in Japanese).
[8] 刘静. 地效飞机着水载荷数值分析[D]. 南京: 南京理工大学, 2010.
LIU J. The research on water load of wing-in-ground effect craft[D]. Nanjing: Nanjing University of Science and Technology, 2010 (in Chinese).
[9] VON KARMAN T. The impact of seaplane float s during landing: NACA TN 321[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1929.
[10] WAGNER V H. Phenomena associated with impact s and sliding on liquid surfaces[J]. Z Angew Math Mech, 1932, 12(4): 193-215.
[11] MONAGHAN R J, CREWE P R. Formulae for estimating the forces in seaplane—Water impacts without rotation or Chine immersion: NACA RN2804[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1949.
[12] MILLER R W. Theoretical analysis of hydrodynamic impact of a prismatic float having freedom in trim: NACA TN2698[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1952.
[13] SIM J L, SCHNITZER E. A theoretical investigation of the effect of partial wing lift on hydrodynamic landing characteristics of V-bottom seaplane in step impacts: NACA TN2815[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1952.
[14] WILLELM P. Theory of the landing impact of seaplanes: NACA TM624[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1931.
[15] STEINER M F. Analysis of planing data for use in predicting hydrodynamic impact loads: NACA TN1694[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1948.
[16] SCHNITZER E. Theory and procedure for determing loads and motions in Chine—Immersed hydrodynamic impacts of prismatic bodies: NACA TN2813[R]. Washington, D.C.: National Advisory Committee for Aeronautics, 1952.
[17] 褚林塘, 叶树林. 水上飞机文集[M]. 北京: 航空工业出版社, 2011.
CHU L T, YE S L. Collected works of seaplane[M]. Beijing: Aviation Industry Press, 2011 (in Chinese).
Theoreticalcalculationandexperimentonimpactloadsoflandingofwing-in-groundaircraftonwatersurface
CHULintang1,2,*,WUBin2,3,WANGMingzhen2,3,SUNFeng2,3
1.ChinaAviationIndustryGeneralAircraftCo.,Ltd,Zhuhai519030,China2.KeyLaboratoryofHigh-speedHydrodynamicAviationScienceandTechnology,Jingmen448035,China3.AVICSpecialVehicleResearchInstitute,Jingmen448035,China
Thesymmetricstepofhulllandingofthewing-in-ground(WIG)aircraftonwatersurface,whichisthemostserioussituation,isconsidered.Allthefactorsinfluencingtheimpactareanalyzed.AtheoreticcalculationmethodisproposedbasedontheassumptionofstriptheoryofshipmotioncombiningwithVonKarman’smomentumequationforhydrodynamicsandWagner’sformulaforcalculationofaddedmass.Experimentalresultsoftheimpactingloadsarecomparedwiththoseoftheoreticalcalculation.Itisshownthattheexperimentresultsareingoodagreementwiththecalculationresults,indicatingthatthetheoreticalevaluationcanprovidetoagreatextentusefulinformationforthedesignoftheWIGaircraft.
wing-in-ground(WIG)aircraft;hydrodynamicimpactload;symmetricstep;striptheory;addedwatermass
2016-01-11;Revised2016-08-08;Accepted2016-08-29;Publishedonline2016-09-061003
URL:www.cnki.net/kcms/detail/11.1929.V.20160906.1003.002.html
CivilAircraftSpecialResearchProgram(MJ-2015-F-028)
2016-01-11;退修日期2016-08-08;录用日期2016-08-29; < class="emphasis_bold">网络出版时间
时间:2016-09-061003
www.cnki.net/kcms/detail/11.1929.V.20160906.1003.002.html
民用飞机专项科研项目 (MJ-2015-F-028)
*
.Tel.:0756-3976018E-mailclt8208@126.com
褚林塘, 吴彬, 王明振, 等. 地效飞机着水冲击载荷理论计算与试验J. 航空学报,2016,37(12):3698-3705.CHULT,WUB,WANGMZ,etal.Theoreticalcalculationandexperimentonimpactloadsoflandingofwing-in-groundaircraftonwatersurfaceJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3698-3705.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0245
V212.13
A
1000-6893(2016)12-3698-08
褚林塘男, 研究员。主要研究方向: 水上飞机水动力设计与试验、 计算流体力学。Tel.: 0756-3976018E-mail: clt8208@126.com
*Correspondingauthor.Tel.:0756-3976018E-mailclt8208@126.com
