基于运动学方法的小卫星串行编队模型误差研究

赵征宇，蔡远文，刘高强，姚静波，王 刚

(1.装备学院 研究生管理大队，北京 101416；2.装备学院 航天装备系，北京 101416)



基于运动学方法的小卫星串行编队模型误差研究

赵征宇1，蔡远文2，刘高强1，姚静波2，王 刚1

(1.装备学院 研究生管理大队，北京 101416；2.装备学院 航天装备系，北京 101416)

针对小卫星串行编队构型设计，采用运动学方法建立串行编队相对运动数学模型。考虑偏心率等于零与不等于零时的两种情形，分别对所构建的运动学模型进行分析；采用MATLAB对相对运动学模型中包含的参考卫星半长轴与初始平近点角差进行仿真，将运动学模型计算结果与精确模型计算结果进行对比分析，得出初始平近点角差对编队模型误差的影响相对更大，为后续小卫星编队综合构形设计奠定基础。

小卫星；串行编队；运动学方法；距离误差；误差比值

0 引言

现代小卫星技术不断创新发展，不但有效弥补了传统大卫星的不足，还在卫星应用方面推陈出新，使得星座与编队的发展前景不断开阔[1]。卫星编队技术在国外发展的相对较早，已经进入探索应用阶段，例如“重力和气候实验卫星”(GRACE-1/2)，目的在于获取高精度和高空间分辨率的静态以及时变重力场，于2002年3月17日发射升空。国内大都还处在理论研究阶段，也进行了相关技术的探索试验。

基础编队构形是编队构形中形式简单，容易理解与实现的构形，充分了解掌握基础构形，有利于进行复杂的编队构形设计。其中，串行编队基础构形是编队基础构形中最简单的基础构形。下面应用运动学方法对其进行建模分析，与精确模型进行比较，确定轨道根数对模型误差的影响[2]。

1 运动学方法建模

运动学方法是基于空间几何关系利用参考卫星与伴随卫星的轨道根数差或相对轨道根数在参考卫星坐标系中描述相对运动的方法[3]。采用轨道根数作为描述参数分析相对运动，能够在一定程度上克服相对运动的线性化动力学方程对问题背景的约束，可以在更广泛的条件下分析相对运动。此外，采用轨道根数描述相对运动便于编队构形的设计与控制。

本节基于相对运动运动学方法的优势，应用运动学方法进行小卫星编队的相对运动建模。针对卫星各参数，以下标表示参考卫星，以下标表示伴随卫星。将两卫星的轨道根数差分别记为Δa、Δe、Δi、ΔΩ、Δω、ΔM。所有的角度度量以逆时针方向为正[4]。

分别将地心赤道惯性坐标系、参考卫星轨道坐标系与伴随卫星轨道坐标系记为坐标系E、C、B。由此，从地心赤道惯性坐标系到参考卫星轨道坐标系和伴随卫星轨道坐标系的转移矩阵[5]分别为：

(1)

(2)

式中，Mj(θ)表示绕瞬时坐标轴j(j=1,2,3)旋转角度的初等转移矩阵：

(3)

(4)

在参考卫星轨道坐标系中建立相对运动方程，如公式(5)：

(5)

其中：Rc和Rb分别为参考卫星和伴随卫星的地心距，采用轨道根数的形式表示如公式(6)：

(6)

公式(5)是相对运动的运动学方程，它利用两颗卫星的轨道根数，在参考星轨道坐标系中描述了伴随卫星的相对运动。如果已知两颗卫星的轨道根数，则可由该式精确求解伴随卫星相对于参考卫星的相对运动轨迹。该方法是基于坐标变换的集合方法，原理通俗易懂，但不足之处在于展开式比较复杂，不利于开展相对运动的特性分析，需要进一步进行简化。

若为小量，则有：

(7)

因为Δi、ΔΩ、Δu均为小量，于是有如下线性化表示：

(8)

其中：

(9)

(10)

将公式(8)～(10)代入公式(2)，并略去高阶项，可得公式(11)：

(11)

其中：

(12)

将公式(11)带入公式(5)，可得公式(13)：

(13)

2 串行编队构形建模

串行编队是编队构形中最基础的编队构形，其特点是两颗小卫星在同一轨道上，相距需求的距离，一前一后串行飞行。其轨道根数如下要求：除平近点角不同之外，其余5个轨道根数完全相同。

下面针对串行编队相对运动运动学模型误差，分为两种情况分别进行仿真分析。

2.1 偏心率为零时的串行编队构形

依据运动学方法建模可知：

(14)

由于参考星与伴随星的轨道偏心率都为零，可得公式(15)与公式(16)：

(15)

(16)

则相对运动运动学方法所建立的串行编队构形模型如公式(17)：

(17)

当参考轨道为圆轨道时，参考星与伴随星之间的几何关系如图1所示。

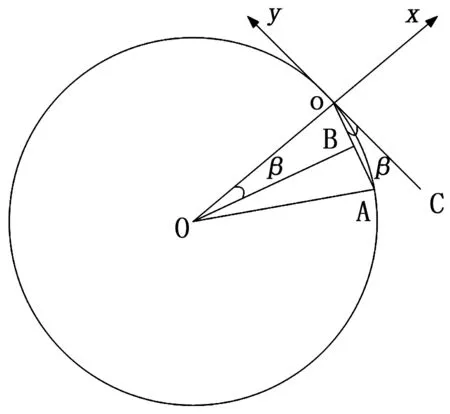
图1 参考星与伴随星几何关系图

图中

oA

与

OB

垂直；∠

oOB

与∠

AoC

相等，都等于

β

；

oA

为参考星与伴随星之间的距离

r

。所以，

ΔM

=∠

oOA

，由图1可知：

(18)

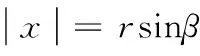
(19)

(20)

当参考轨道的半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角都确定的情况下，通过改变初始平近点角来改变两星之间的相对距离，并分析运动学方法所建立模型的误差。

当半长轴固定为7 000 km时，改变两星初始平近点角差，应用运动学模型计算得到相对距离与各轴方向的分量，通过与精确几何模型计算所得的结果进行对比分析其误差。其中精确几何模型计算所得数据以下标1表示，运动学模型计算所得数据以下标2表示。表1是运动学模型相对距离的误差变化情况表。

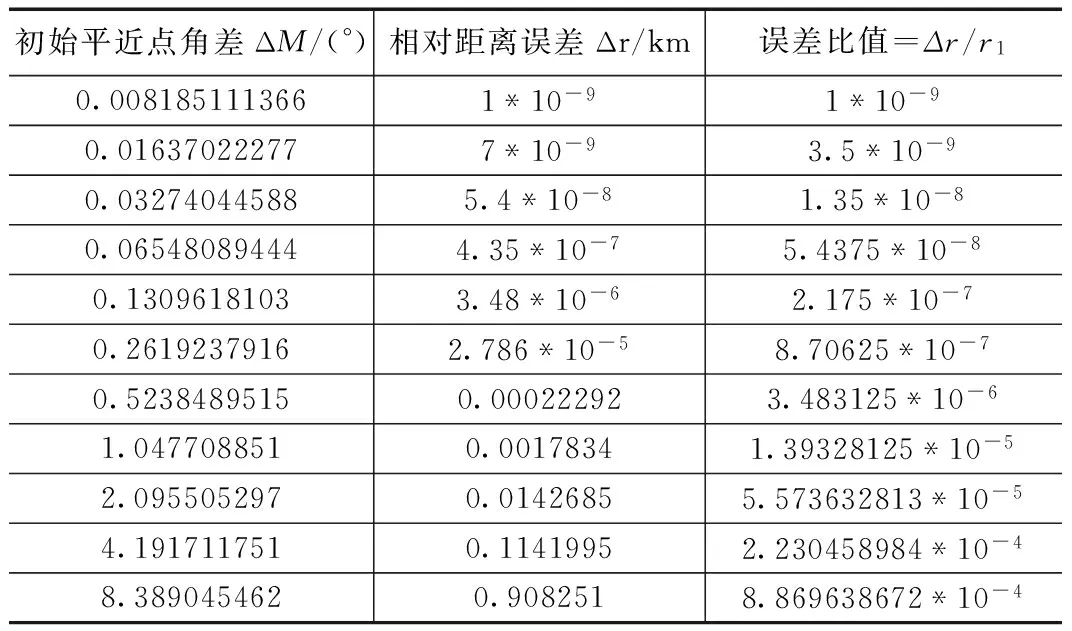
表1 运动学模型相对距离的误差变化表

由表1可知，随着初始平近点角差的增加，运动学模型计算所得的相对距离与精确相对距离之间的误差逐渐增加，距离误差相对于精确相对距离的比值也逐渐变大；同时可以得出，模型误差相对于半长轴可忽略不计，相对于相对距离量级保持在10-4以上，可以进行简化处理。表2是运动学模型x轴向距离误差随初始平近点角差变化情况表。

表2 运动学模型x轴向距离的误差变化表

由表2可知，随着初始平近点角差的增加，运动学模型计算所得的x轴向距离与精确x轴向距离之间的误差也在增加，距离误差相对于精确相对距离的比值也在变大。初始平近点角差小于1.047708851°时，模型x轴向距离误差相对于精确相对距离比值保持在10-3以上；初始平近点角差在2.095505297°与8.389045462°之间时，模型x轴向距离误差相对于精确距离的比值保持在10-2量级上。表3是运动学模型y轴向距离误差随初始平近点角差变化情况表。

表3 运动学模型y轴向距离的误差变化表

由表3可知，随着初始平近点角差的增加，运动学模型计算所得的y轴向距离与精确y轴向距离之间的误差也在增加，距离误差相对于精确相对距离的比值也在变大；同时可以得出模型误差相对于半长轴为小量可以忽略不计，相对于相对距离来说也是小量，量级保持在10-3，可以进行简化处理。

综合对比分析可知：

1)在同一条件下，运动学模型计算所得的相对距离误差在数值与比值都是最小的，y轴向次之，x轴向最大，由此可以看出在运动学模型公式推导过程中x轴向简化的相对较多，导致模型在x轴向模型误差相较于相对距离与y轴向都大。

2)基于串行编队构形特点，三轴向距离在相对距离中所占的比重不同，其中y轴向距离数值最大，所占比重最大，对于相对距离的影响最大，所以相对距离的误差与y轴向的误差最接近。

3)在初始平近点角差逐渐增大的前提下，保持半长轴不变，运动学模型计算所得的相对距离、x轴向距离与y轴向距离的误差都在增加，运动学模型在相对距离与y轴向距离误差更小，在x轴向距离误差相对于前两者较大；相对于半长轴来说，模型误差都可以忽略，但相对于相对距离来说，x轴向需要进行适当考虑，以减少模型误差。

上面对初始平近点角差进行了分析，下面对半长轴进行计算分析。保持初始平近点角差不变，改变半长轴，观测模型相对距离、x轴向与y轴向的距离误差变化情况。保持初始平近点角差，则模型的相对距离、x轴向距离与y轴向距离误差随半长轴变化情况如表4～表6所示。

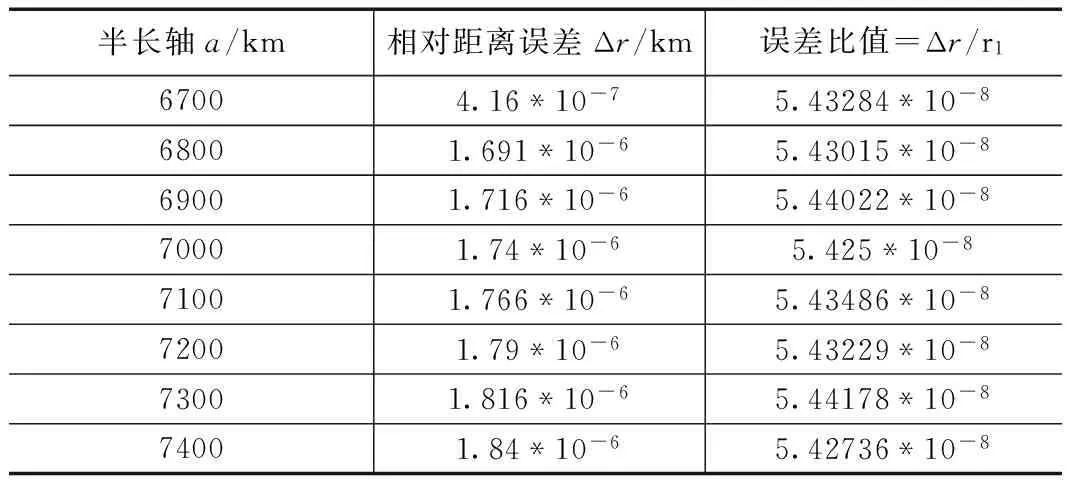
表4 运动学模型相对距离的误差变化表

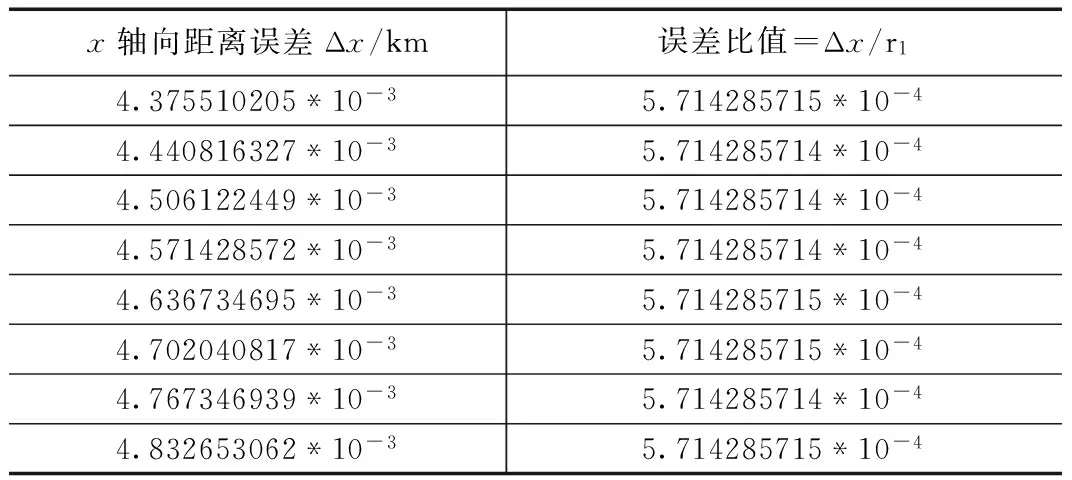
表5 运动学模型x轴向距离的误差变化表

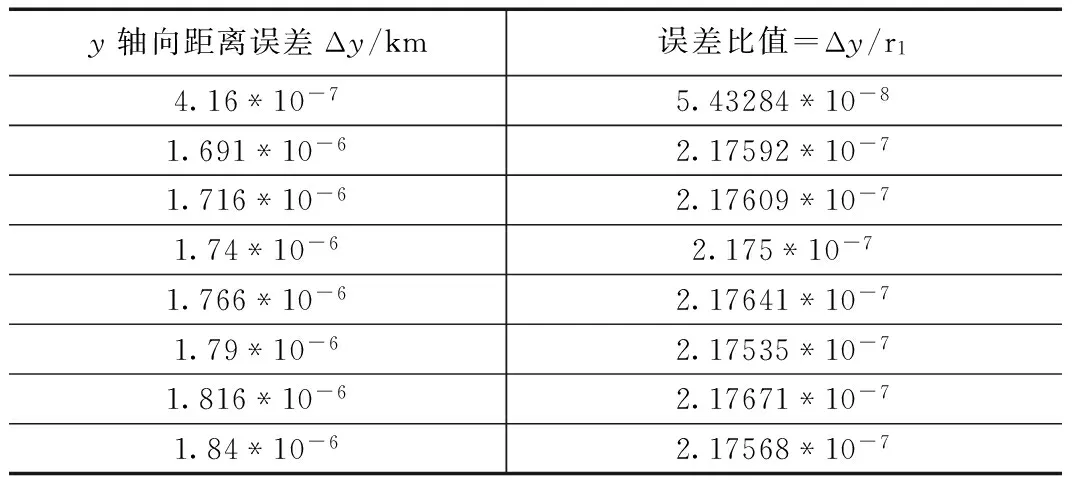
表6 运动学模型y轴向距离的误差变化表

由表中数据可知，当初始平近点角差保持不变，半长轴逐步增加时，运动学模型计算所得相对距离、x轴向距离与y轴向距离误差逐渐增加，但其相对于精确相对距离之间的比值基本保持稳定，在相同量级上存在微小差别。

综上分析可知，半长轴的变化对运动学模型计算所得的相对距离与各轴向距离的误差影响基本保持不变；相对于初始平近点角差变化对模型距离误差的影响小。所以，在进行串行编队构形设计时，需要充分考虑初始平近点角差，以减少模型误差对于编队构形的设计中带来的误差。

2.2 偏心率不为零时的串行编队构形

当参考星轨道偏心率为一阶小量并略去二阶及以上小量时，有：

E≈M+esinM

(21)

f≈M+2esinM

(22)

则相对运动运动学方法所建立的串行编队基础构形模型如下：

(23)

其中：

(24)

(25)

取半长轴为7 000 km，偏心率为0.001，使初始平近点角差从0.008185111366°变化到8.389045462°，应用MATLAB进行仿真，来分析x轴向、y轴向、z轴向与相对距离的误差变化情况。

首先，对x轴向距离误差进行仿真。x轴向距离误差数值变化情况如图2所示，图中a、b、c、d分别表示选择ΔM=0.008185111366°、0.06548089444°、0.5238489515°、8.389045462°时，x轴向距离误差的变化情况。

图2 x轴向距离误差随时间t变化

由图2可知，x轴向距离误差随着初始平近点角差的增加逐渐增加，量级从10-5增加到10-1。而其距离误差相对于精确模型中的相对距离的比值如图3所示。

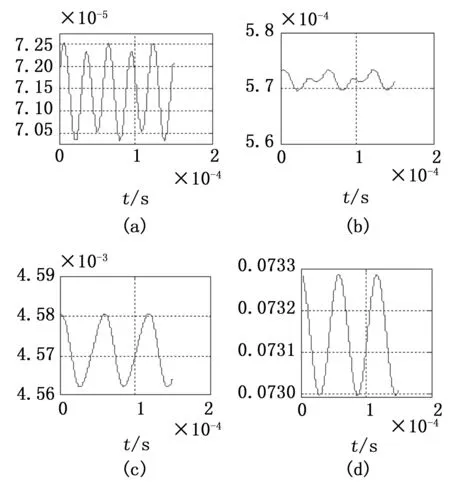
图3 x轴向距离误差与精确相对距离比值随时间t变化

由图3可知，

x

轴向距离误差与精确相对距离的比值随着初始平近点角差的增加而增加，比值的量级没有数值的量级变化那么大，比值量级从10

-5

变化到10

-2

。

其次，对y轴向进行仿真，y轴向距离误差变化情况如图4所示。

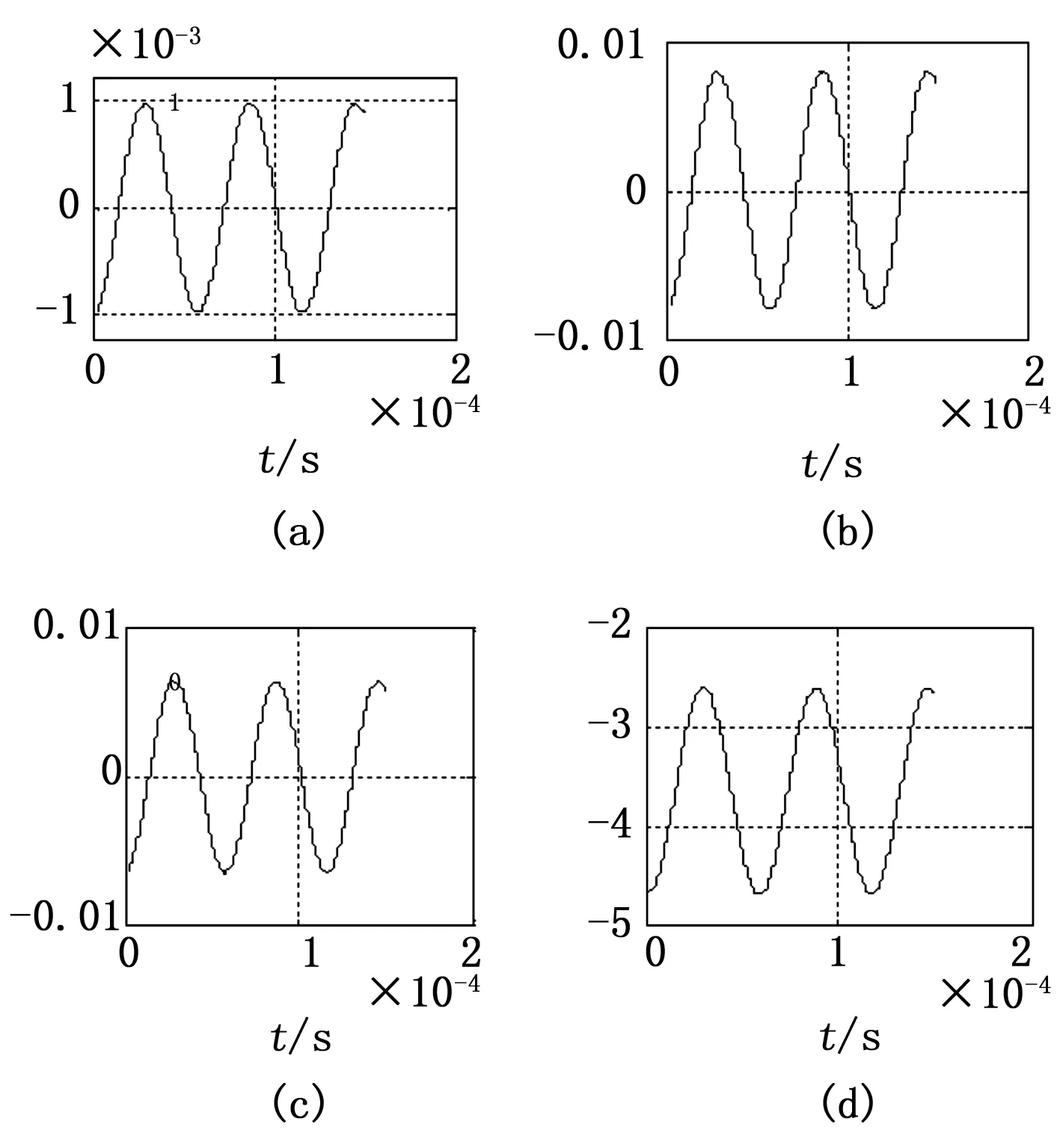
图4 y轴向距离误差随时间t变化

由图4可知，y轴向距离误差随着初始平近点角差的增加逐渐增加，量级从10-3增加到100。相较于x轴向距离误差来说，变化幅度没有x轴向大。而其距离误差相对于精确模型中的相对距离的比值如图5所示。

图5 y轴向距离误差与精确相对距离比值随时间t变化

由图5可知，

y

轴向距离误差与精确相对距离的比值没有随着初始平近点角差的增加而增加，比值的量级基本保持不变，在10的负3次量级上。说明

y

轴向的距离误差相较于相对距离来说是一个小量。对比

x

轴向可知，

y

轴向误差比值相对于

x

轴向误差比值变化小。

由仿真可知，运动学模型与精确模型的z轴向距离计算都为零，不存在误差。

综合对比3个轴向可知：

1)x轴向距离误差在数值与比值上的变化幅度最大；

2)y轴向距离误差在数值上有明显变化，但其比值保持在同一量级上；

3)而z轴向没有距离，不存在距离误差。

因此，初始平近点角的差异对x轴向的影响最大。

最后，对相对距离进行仿真，相对距离误差数值变化情况如图6所示。

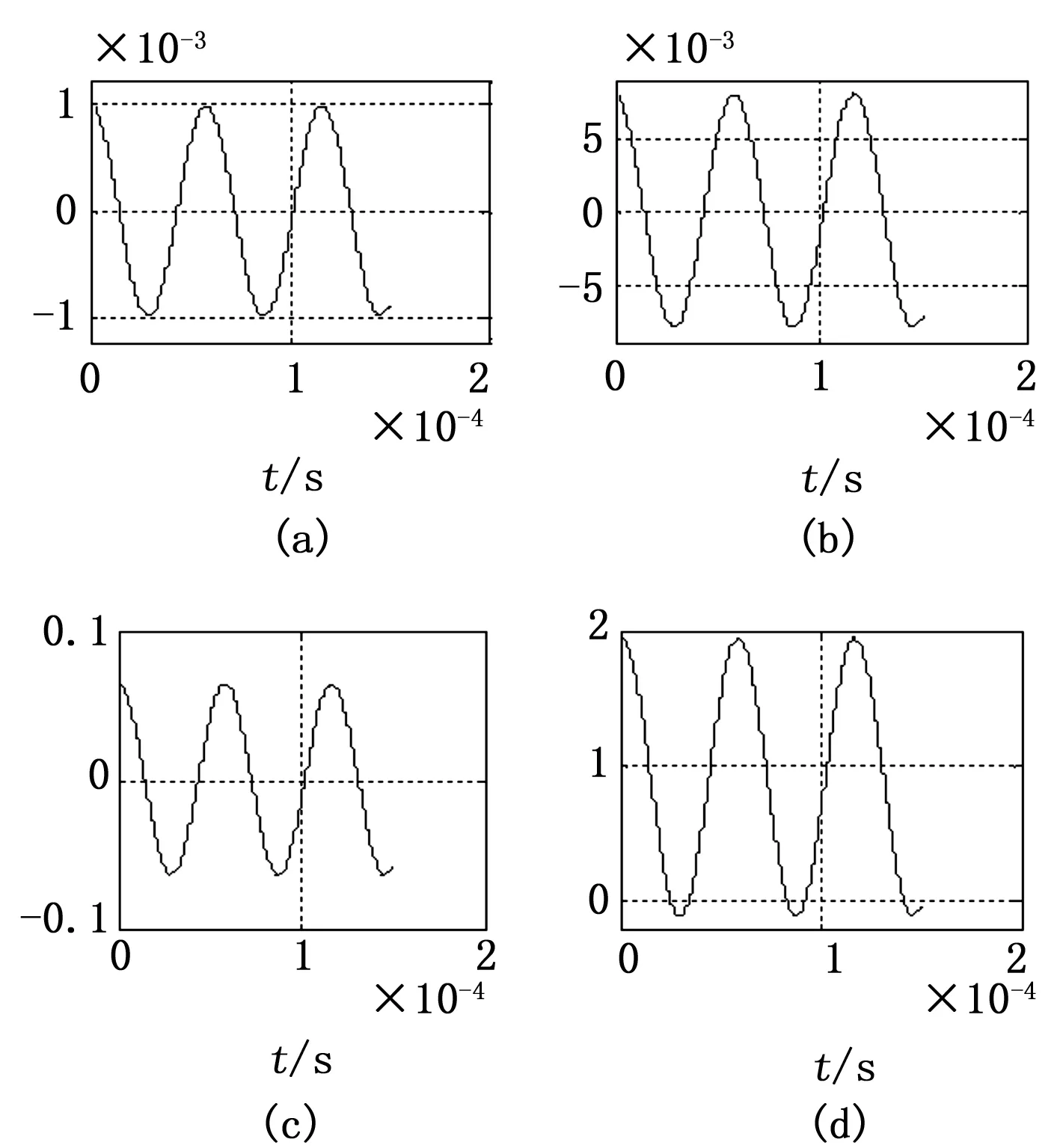
图6 相对距离误差随时间t变化

由图6可知，相对距离误差随着初始平近点角的增加逐渐增加，量级从10的负3次增加到10的0次。而其距离误差相对于精确模型中的相对距离的比值如图7所示。

图7 相对距离误差与精确相对距离比值随时间t变化

由图7可知，在(a)～(c)之间，相对距离误差与精确相对距离的比值没有随着初始平近点角差的增加而增加，比值的量级基本保持不变，在10的负3次量级上。而在(d)中，比值有所增加，但量级基本保持不变。说明相对距离误差相较于相对距离来说是一个小量。

综合对比3个轴向与相对距离误差的仿真分析图可以发现，相对距离与y轴向的距离误差变化比较接近。分析运动学模型式也可以得出相同的结论，y轴向距离数值远大于x轴向距离数值，在计算相对距离时y轴向距离所占的比重远大于x轴向距离。由此可知，相对距离误差随初始平近点角变化的趋势与y轴向变化基本一致。同时x轴向受初始平近点角差的影响较大，误差变化幅度较大，在进行构形设计时，需要充分考虑x轴向误差对构形功能的影响，适当选取初始平近点角差，以减少误差。

3 结论

在现代小卫星蓬勃发展的背景下，编队应用模式的研究不断深入。运用运动学方法对串行基础编队构形进行建模仿真，通过与精确模型的对比分析，得出：

1)在低轨串行编队中，初始平近点角差不同造成的模型误差比半长轴不同造成的模型误差来的大。在编队设计时，相较于半长轴，需要更加注意初始平近点角的选择，以减少模型误差；

2)初始平近点角差在模型3个轴向中的影响不同，对于x轴向的影响最大，y轴向次之，z轴向由于编队特性，没有造成影响。在进行设计时，更需要注意对x轴向误差的控制，使之符合要求；

3)由模型式与仿真分析图可知，y轴向距离在3个轴向中所占的最大，相对距离的变化情况与y轴向的变化情况更加接近。

[1] 闻 新,马文弟, 周 露. 小卫星编队飞行的应用模式分析及展望[J]. 中国航天, 2005(8):40-43.

[2] 肖玉婷, 朱立东. 一种卫星编队构形设计方法[J]. 计算机仿真, 2013, 31(2):126-130.

[3] 冯永新, 武金花. 基于STK的小卫星编队飞行仿真[J]. 火力与指挥控制, 2011, 36(3):67-70.

[4] 曹喜滨, 张锦绣, 王 峰, 等. 航天器编队动力学与控制[M]. 北京: 国防工业出版社, 2013.

[5] 孟云鹤. 航天器编队飞行导论[M]. 北京: 国防工业出版社, 2014.

Research on Model Error of Small Satellite Serial Formation Based on Kinematic Method

Zhao Zhengyu1，Cai Yuanwen2，Liu Gaoqiang1，Yao Jingbo2，Wang Gang1

(1.Department of Graduate Management, Equipment Academy，Beijing 101416，China;2.Department of Space Equipment, Equipment Academy，Beijing 101416，China)

In aiming to design the configuration of small satellite serial formation, the relative motion model is built based on kinematic method. Considering the two cases that eccentricity is equal to zero and not, two kinematic models were analysed respectively. The semimajor axis and initial mean anomaly difference of

atellite in relative motion model are simulated based on Matlab software, and the calculation results of kinematic model and accurate model are compared.The result show that the initial mean anomaly difference has larger influence on the model error of the formation, which is useful for the subsequent comprehensive configuration design of small satellite formation.

small satellite; serial formation; kinematic method; range error; error ratio

2016-01-06；

2016-01-27。

赵征宇(1990-)，男，浙江金华人，硕士研究生，主要从事卫星编队技术方向的研究。

蔡远文(1967-)，男，四川彭州人，教授，博士生导师，主要从事飞行器测试发射控制技术、计算机仿真技术方向的研究。

1671-4598(2016)06-0244-04

10.16526/j.cnki.11-4762/tp.2016.06.067

V412.41

A