无人机三维实时航迹规划

席剑锐,杨金孝,张博亮,陈志星

(西北工业大学 电子信息学院,西安 710129)



无人机三维实时航迹规划

席剑锐,杨金孝,张博亮,陈志星

(西北工业大学 电子信息学院,西安 710129)

无人机航迹规划是无人机任务规划中最重要也是最复杂的环节，针对基本粒子群航迹规划算法后期容易陷入局部最优解、算法容易“早熟”、规划出的航迹精度不高等问题，提出了一种以并行方式进行的双种群粒子群航迹规划算法;双种群粒子群算法由两个向相反方向搜索的种群构成，这两个种群协同优化，扩展了搜索范围，克服了基本粒子群算法后期容易陷入局部最优解的问题，提高了航迹的精度;如果无人机在飞行过程中检测到突发威胁，则寻找邻近航迹点作为实时重规划点，规划其到目标点的航迹;通过仿真验证了算法的有效性，并满足了实时性的要求。

无人机;三维航迹规划;双种群粒子群算法;实时性

0 引言

无人机是“无人驾驶空中飞行器”(UAV)的简称。随着航空航天技术的日新月异以及高新技术的快速发展，无人机作为一种新兴的航空军事力量在现代战场中的作用越来越明显，必将左右未来战场的格局[1]。无人机航迹规划(route planning for unmanned aerial vehicles)是无人机任务规划(mission planning)的一项重要组成部分，对于无人机圆满完成作战任务有着非常重要的意义。一条好的航迹不但可以符合无人机自身的约束以及各种地理环境的约束，而且能够有效地躲避战场上的各种威胁[2]。无人机航迹规划问题究其本质是最优化问题，具体的来说，最优化问题就是在约束条件的限定范围之内寻找一组数据，该组数据能够使函数(或系统)的一些指标特性达到最小或者最大值。航迹规划算法对于无人机航迹规划至关重要，目前用在无人机航迹规划上的算法有许多，根据不同的标准可以将航迹规划算法进行划分。根据航迹规划决策的计算方式来分，可以分成智能优化算法和传统的经典算法。由于传统经典算法存在着：计算的工作量较大、容易陷入局部最优解以及不具有智能搜索功能等缺点。因此，目前的主流方式是采取智能优化算法对航迹规划问题进行求解。在智能优化算法中，遗传算法、A-Star算法、蚁群算法和粒子群算法是经常用到的算法。基本粒子群算法鲁棒性强、计算量小、不需要梯度的信息、易于实现，但算法容易陷入局部最优解，算法容易“早熟”。因此，本文提出了一种双种群粒子群航迹规划算法。

1 航迹规划建模

1.1 威胁信息转化

在无人机航迹规划中，需要对威胁信息进行回避。威胁信息主要包括两种类型：探测威胁(包括可见光、红外射线、音响、雷达等)和火力威胁(机载、车载导弹系统以及不同口径的火炮等)。如果利用传统的方法将威胁信息转化为数学上的约束条件，那么在每一次迭代的过程中代价函数的计算量将大大增加，使航迹规划过程变得非常复杂。因此，本文采取了威胁信息融合技术，将飞行区域内已知地形和威胁信息融合成一种综合的地形，将威胁的规避转化为地形的规避，降低了航迹规划过程中的计算量，使得实时性要求得以满足。

对威胁信息融合需要首先将威胁等效为地形高程数据，如式(1)所示：

(1)

式中,T(x，y) 为威胁等效高度在点(x，y)的值；z0为威胁中心处的地形高度；r 为航迹点与威胁中心的水平距离；Rmax为威胁的最大作用半径。

然后将各种威胁等效的高程数据离散化，并采用如式(1)的方法，从而得到融合后的综合地形高程数据h。

(2)

式中，hth为地形高程数据；htd1，htd2，…，htdm为 m个威胁的等效高程数据。

对威胁的融合采用取极大值而非高程值直接相加的方法，这样能够更好地利用地形隐蔽信息的作用。如果在某区域内，地形点的高度值大于该区域威胁等效后的高度值，那么说明该区域内的地形对威胁具有很好的隐蔽作用。因此可以不考虑威胁产生的影响，而只考虑该区域内的地形信息。

1)高炮威胁。设高炮的水平坐标为(x0，y0)，在各个方向上的作用半径相同均为R0，则高炮等效地形程为：

(3)

式(3)是旋转抛物面的方程，因此等效地形跟山峰模型相似。

2)雷达威胁。假设在雷达最大作用距离Rfmax处无人机被发现的概率为某一定值，那么可用如下等效高程来描述：

(4)

式(4)中，a为小于1的常数；b为大于1的常数；HR为一很大常数。

治疗后两组的Vmax、PAPs值低于治疗前，同组治疗前后比较差异有统计学意义（P＜0.05）；观察组治疗后也低于对照组，差异有统计学意义（P＜0.05），见表3。

1.2 最小安全曲面

如果在综合等效曲面h(x, y)上叠加一个最佳安全离地高度hc，那么将得到一个新的曲面，显然无人机在该曲面上飞行是安全的，将该曲面称为安全曲面。最佳安全离地高度hc需要根据区域地理特征及已知威胁杀伤特性来确定。国外文献认为，最佳离地高度：海面上空15～30 m，陆地平原地区上空为60～80 m，丘陵山区上空为120 m左右。在得到了安全曲面后，最佳航迹的存在空间便缩小到安全曲面上了，从而可把三维航迹规划的优化过程限制在一个二维曲面上，大大地降低了计算量，满足了航迹规划中实时性的要求。

1.3 代价函数的确立

假设S:S={s1,s2,s3,…, sm}表示规划空间的所有节点组成的集合,E:E={e1, e2, e3,…, en}是两两相邻可通节点组成的可飞航迹集合。若第i段航迹ei(ei∈E)是由两个相邻节点si和si+1和(si,si+1∈S)构成，该段航迹的代价可由代价函数F求得，航迹规划的目的就是要使所以航迹代价的总和最小[3]。前文已经将无人机在作战任务中可能遇到的威胁纳入考虑，在实际飞行过程中，无人机自身的机动性能和生存概率也是影响航迹规划的重要因素。在实际飞行过程中，无人机自身的机动性能和生存概率也是影响航迹规划的重要因素。这其中包括航迹总长度、最大转弯角、最大爬升/下滑角、最小航迹长度、最低飞行高度和靠近目标程度。若将规划空间离散化，航迹可以用节点的形式表示[4]，则总代价函数F：

(5)

其中：fi为各子代价函数，ki为每个子函数的加权系数，每个权重系数的大小可以根据无人机自身的机动性能以及无人机具体的飞行环境和任务而改变，但应满足：

(6)

2 基本粒子群算法

2.1 标准粒子群算法

标准粒子群算法中，每个粒子(Particle)代表一个可能的解，所有的粒子组成群体(Swarm)。粒子在解空间中根据自身的历史信息和群体信息共同决定其“飞翔(fly)”的速度和方向，以此来寻找最优解。假设在D维搜索空间中进行问题求解，群体由m个粒子组成，Swarm={x1(t), x2(t),…,xm(t)}。t时刻第i个粒子在搜索空间中的位置向量为xi(t)=[xi1(t),xi2(t),…,xid(t)]，i=1,2，…，m，xik(t)表示这个粒子在第k维坐标中的位置，同时也是问题的一个可能解。与该个体位置向量相对应的是其速度向量vi(t)={vi1(t), vi2(t),…,vid(t)}，vik(t)为该粒子在第k维坐标下的速度，描述了此粒子在第k维上的运动情况。标准粒子群算法的邻域函数在每一次迭代中根据粒子自身位置向量、速度向量、个体历史信息、群体信息和扰动产生新的位置状态。标准粒子群算法中第i个粒子在t+1时刻的邻域函数计算公式如下[5]：

(6)

(7)

标准粒子群算法中，个体极值pibest=(pi1, pi2,…, pid)，代表了单个粒子从开始搜索到当前对应的代价函数最小的解；全局极值gibest=(gi1, gi2,…,gid)，代表了整个粒子群从开始搜索到当前对应的代价函数最小的解。粒子群中的每个粒子根据个体极值pibest和全局极值gbest的位置和速度，按照公式6、7来更新自己的位置和速度，使粒子向着最优解移动，从而产生下一代群体，t代表PSO的优化迭代次数，i=1,2,…,n。非负常数c1、c2为学习因子，也称为加速因子，它使粒子可以向群体中的最优个体学习并具有自我总结能力，从而使粒子向个体极值和全局极值两个最优点移动。在粒子群算法中，学习因子对收敛所起的作用并不大，但是对学习因子进行适当的调整可以减少局部最优值的困扰，也可以加快收敛速度。rand1、rand2是介于0～1之间的两个随机数，可以保持群体的多样性。惯性权重ω表示上一迭代时刻搜索速度在下一迭代时刻的惯性保留值，适当设置惯性权重ω的值，可以控制算法探测(exploration)和开发(exploitation)能力。

2.2 惯性权值的调整

本文采取一种多样性反馈的自适应惯性权重调整策略[6]。为了引入这种惯性权重调整策略，首先介绍一种基于熵概念的多样性评价机制。初始化参数，在n维搜索空间内，设粒子集合X={x1, x2, …, xm}，m为粒子数目，xi为n维向量。假设粒子群在搜索空间内最长对角线长度为d(xi, xj)=L，粒子xi和xj连线的方向矢量为v。按照式(8)计算每个粒子(除去xi和xj)在方向为v上的投影，便得到m个一维样本ym。

yi=vTxi

(8)

将xi和xj的连线按长度划分成m个等距离的子区域，统计区域内样本yi的数目hi(i=1，2,3,…,m)，且。计算分布熵：

(9)

上述评价机制量化了粒子在搜索空间内的离散程度，分布熵越大，多样性越好，反之，多样性较差。按照以上评价策略将惯性权重ω按以下方式进行自适应调节：

(10)

由上式可知，ω会随着E(t)做单调变化，因此ω将会随着搜索过程中的多样性来自适应的进行调整。当E(t)较大时，ω随多样性成单调递增趋势，有利于增强算法的全局搜索能力；当E(t)较小时，ω随多样性成单调递减趋势，有利于算法的局部探索能力。

2.3 双种群粒子群算法

双种群粒子群算法受到并行优化思想的启发，设置两个搜索方向相反的主、辅种群协同优化，并通过比较两个种群间代价函数来评价两个种群中粒子位置的优劣，以此来扩大搜索范围，能够快速而准确的响应极值点的变化情况。下面给出双种群粒子群算法的实现思想：随机初始化一组种群后将其平均分成两个相互独立的种群。其中一个种群称为主子群，按照式(6)、(7)的速度、位置更新公式进行迭代搜索；另一个种群称为辅子群，速度更新方法与主子群一致，但按照主子群相反的方向进行迭代搜索，即位置更新按照公式(11)进行[7]：

(11)

每次迭代更新完成之后比较两个种群个体最优位置pibest所对应的代价函数值的大小，代价函数值较大的个体粒子被淘汰。在进行下一次迭代时，主辅种群从当前最优位置出发，向两个相反的方向进行迭代搜索全局最优解gbest。这样在不增加粒子规模的前提下，两个种群相互补充、协同进化，极大程度了扩大了搜索范围，并在搜索空间内极大地发掘出有用信息，有效地降低了算法后期标准粒子群算法易于陷入局部最优解的可能性。同时，双种群粒子群算法并没有增加算法的复杂度，延续了基本粒子群算法高效的搜索效率，满足了对实时性的要求。因此，双种群粒子群算法能够更加快速而准确地响应动态变化的极值，不会产生因算法后期陷入局部最优解而产生的停滞进化的现象。本文将反馈自适应惯性权重与双种群粒子群算法结合，每个粒子代表一个潜在的航迹，则航迹规划流程图如图1所示。

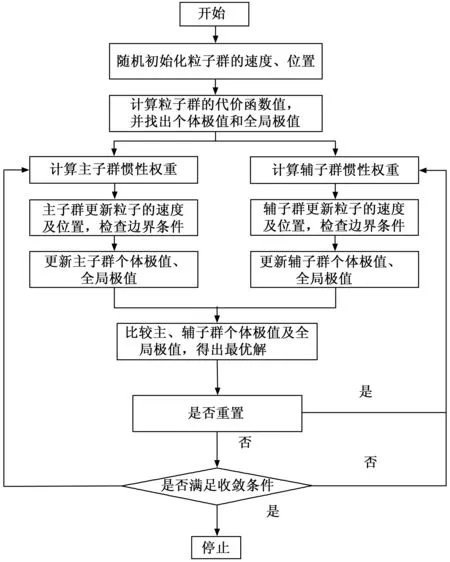
图1 双种群粒子群算法流程图

3 无人机实时航迹规划

在实际应用中，由于反威胁装置的存在，很多威胁是无法预知的，只有当无人机飞行到它的附近时才能通过机载设备感知发现，这种威胁一般称为(pop-up)威胁[8]，如果依然按照整体规划的航迹飞行，会大大地降低无人机安全飞行的概率。因此，当无人机探测到规划空间有突发威胁时，需要对其航迹进行重规划，以保证无人机能够安全地到达目的地并完成飞行任务。

一般处理突发威胁有两种方法：第一种将威胁信息等效成数字地形加载到数字地图中去，进行全局航迹的重规划，这样虽然可以得到较优的航迹，但却以牺牲时间为代价，并且重新规划出的航迹很难与无人机正在飞行的航迹有交汇点，也就是说无人机无法从当前位置飞到规划的航迹上去，那么规划出的航迹也就失去了意义；第二种是进行局部重规划，即在原来整体参考航迹的基础之上进行局部重规划，将威胁等效成数字高程信息后，以无人机当前坐标位置为起点，规划其到终点的航迹路线。这种方法规划时间短，满足了在线航迹规划实时性的要求。因此，本文采用第二种方法对突发威胁进行规避。

4 仿真

本文采用MalabR2008a分别对无人机的整体航迹规划、在线航迹规划进行仿真分析。双种群粒子群算法中选取初始粒子数为20，c1=c2=1.4，最大迭代次数为100次。设置规划空间大小为100*100，第一个山峰模型基准高度为0，中心坐标为(30,30)，山峰高度h1=1000，x轴和y轴的坡度向量依次为xsi=13，ysi=13;第二座山峰基准高度为0，中心坐标为(70,70)，山峰高度h2=800，x轴和y轴的坡度向量依次为xsi=16，ysi=16，无人机最小飞行长度为3，最大转弯角为90°，最大爬升/下滑角为60°，单位步长内无人机所能抬升的最大高度为100。设置两个高炮威胁以及两个雷达威胁，雷达和高炮威胁如表1所示。

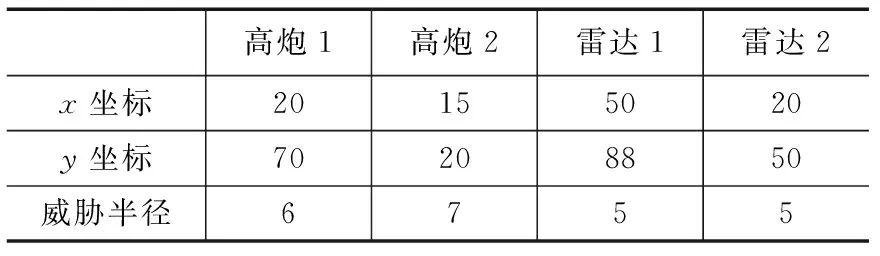
表1 威胁坐标

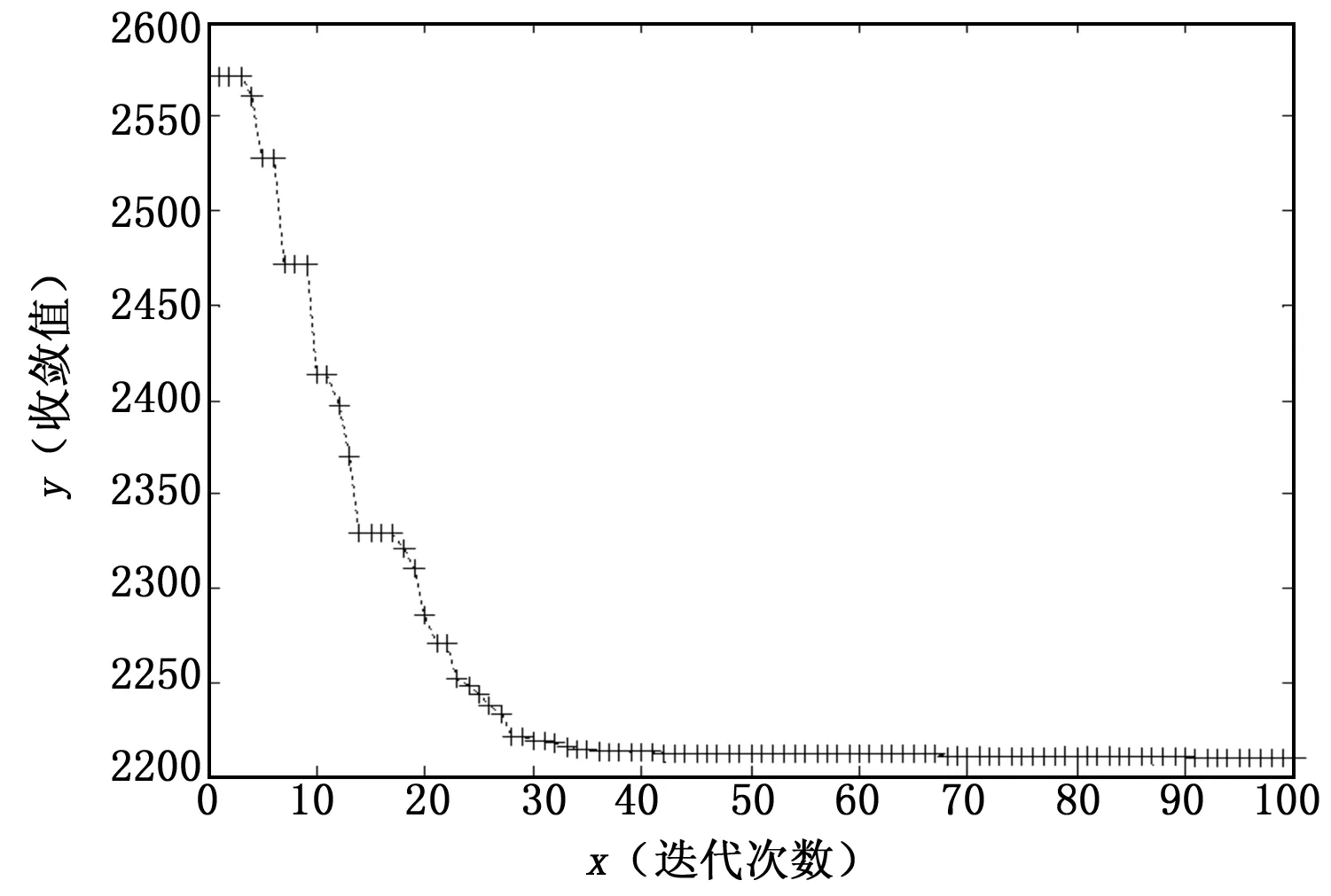
图2 基本粒子群算法循环迭代图

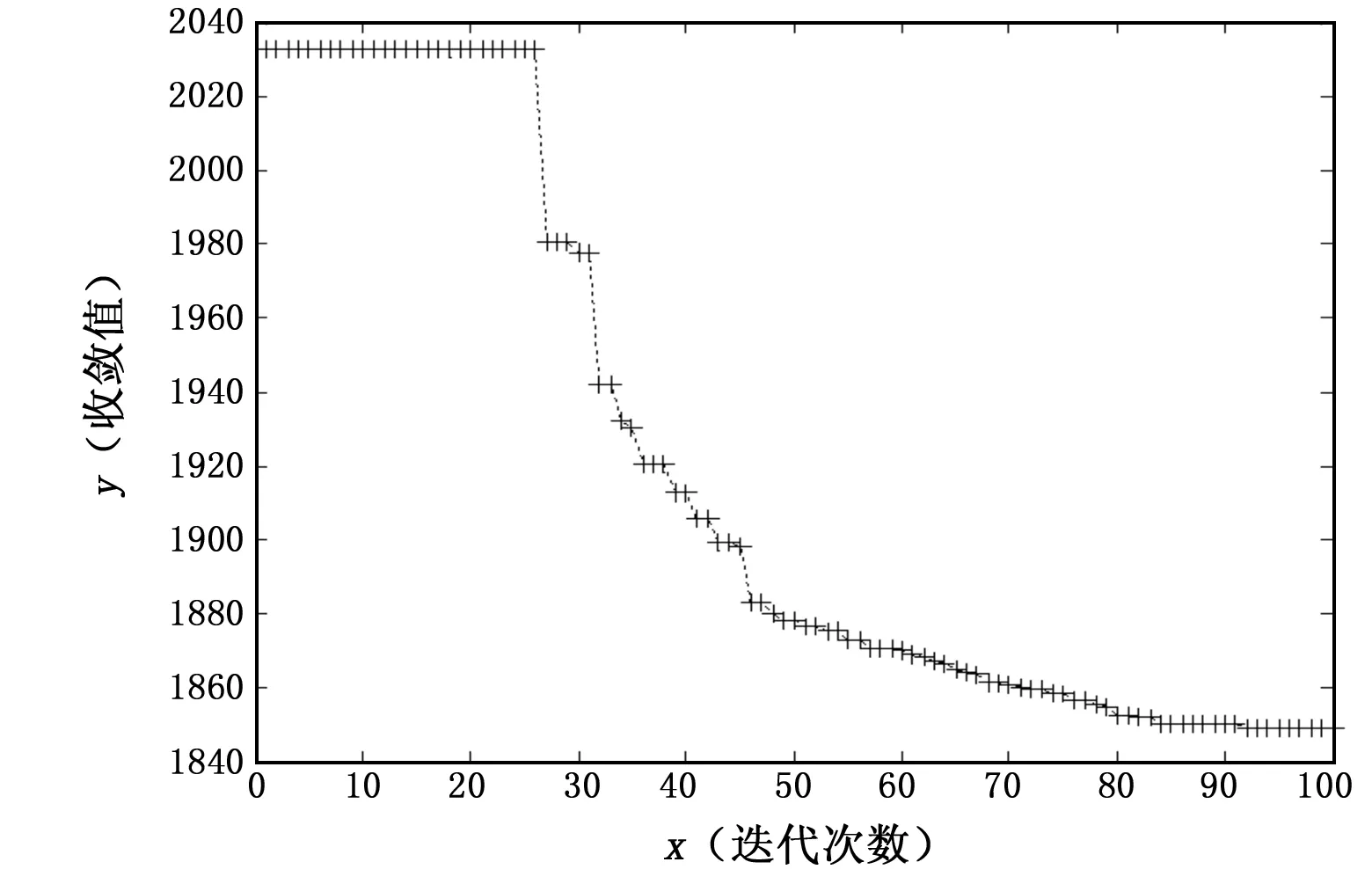
图3 双种群粒子群算法循环迭代图

图2、图3为整体航迹规划的循环迭代图，由循环迭代图可以看出基本粒子群算法大约在28代开始收敛，收敛值约为2 230。而在双种群粒子群算法中，算法大约在80代开始收敛，收敛值约为1 860。这说明双种群粒子群算法在算法后期，可以借助两个种群的协同作用跳出局部最优解，解决基本粒子群算法中的“早熟”问题，从收敛值可以看出，双种群粒子群算法规划的航迹要更加优于基本粒子群算法所规划的航迹，证明了双种群粒子群算法在三维航迹规划中的可行性。

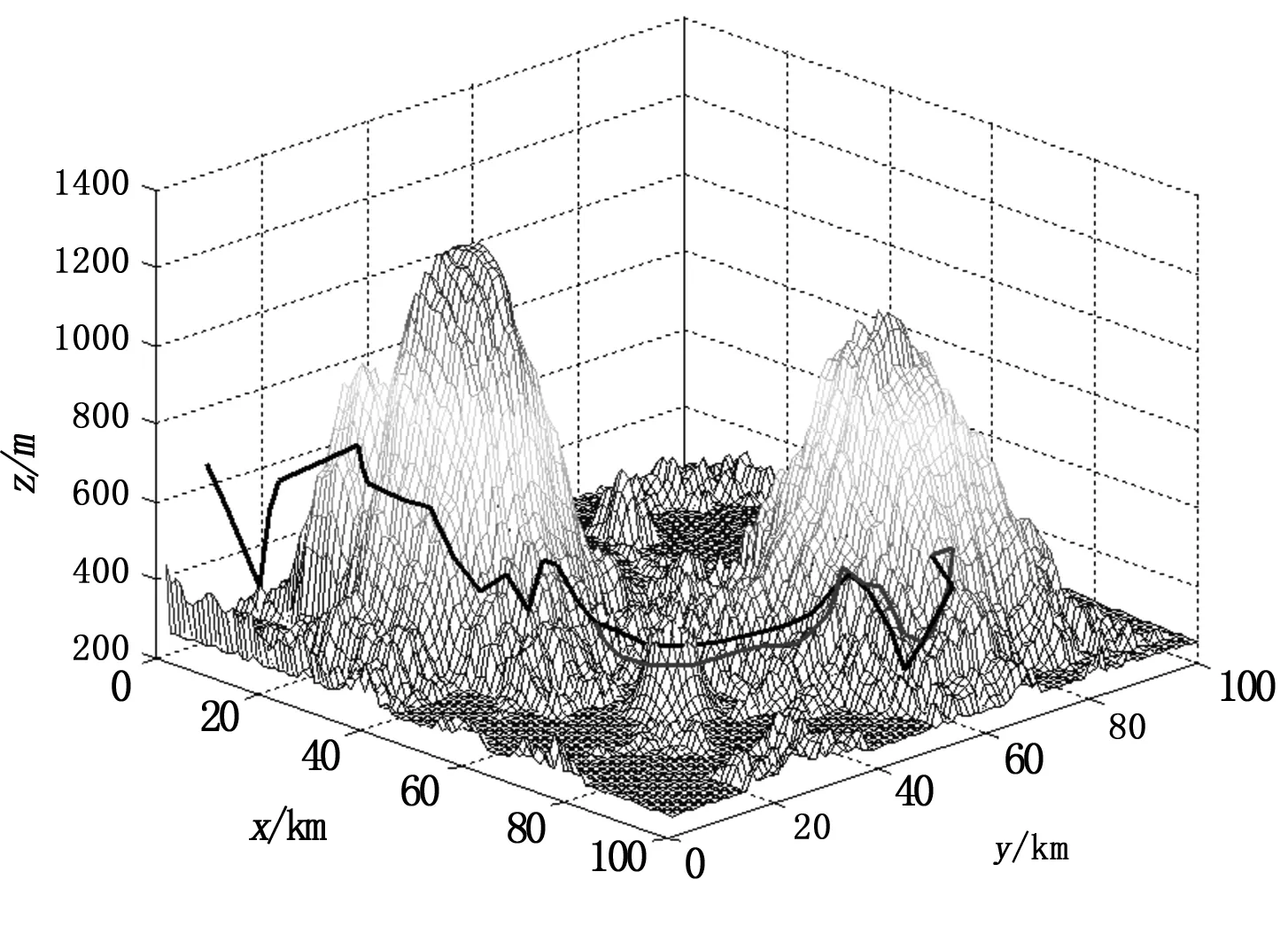
图4 三维实时航迹规划

无人机起始点坐标为(5，5)，终点坐标为(100，50)，假设在其飞行航迹点(58，23)的A处发现坐标中心位于(70，30)的雷达威胁，威胁半径为5，此时无人机对此威胁进行响应，进行航迹重规划。如图5等高线图所示，无人机在原航迹坐标为(60，25)的B处进行了航迹重规划，(a)线代表原先规划的航迹，(b)线为重规划后的航迹。从图中可以得出，如果按照原先规划好的航迹，那么无人机将会暴露在雷达威胁下，而重规划后的航迹躲避掉了雷达威胁，满足了实时性的要求。

5 结论

针对基本粒子群航迹规划算法后期易于陷入局部最优解，

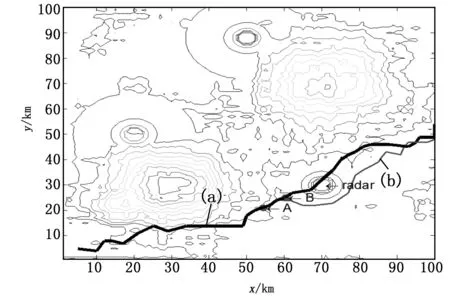
图5 三维实时航迹规划等高线图

规划出的航迹精度不高等问题，本文提出了双种群粒子群航迹规划算法予以改进，同时惯性权重的选择采取多样性反馈的自适应惯性权重调整策略。通过仿真可以看出：改进后的粒子群算法能够跳出局部最优解，提高了航迹规划的精度。同时，针对在真实环境中所出现的突发威胁，采用在整体参考航迹的基础之上进行局部修改，将威胁等效成数字高程信息后，以无人机当前坐标位置为起点，规划其到终点的航迹路线，仿真结果也验证了其有效性。

[1] 丁阿维.我国军用无人机发展趋势及现状分析[J]. 硅谷, 2015(3): 152-153.

[2] Özalp N, Sahingoz O K. Optimal UAV path planning in a 3D threat environment by using parallel evolutionary algorithms[A]. 2013 International Conference on Unmanned Aircraft Systems (ICUAS)[C]. Grand Hyatt Atlanta, Atlanta, GA, 2013: 308-317.

[3] 王绪芝.不确定环境下无人机航迹动态规划及仿真研究[D]. 南京：南京航空航天大学，2013.

[4]姚永杰，席庆彪，刘慧霞. 基于改进遗传蚁群算法的无人机航路规划[J]. 计算机仿真, 2011,28(6):44-47.

[5] Shi Y, Eherhart R C. Parameter selection in particle swarm optimization[A]. Proc.Seventh Annual Conference on Evolutionary Programming[C]. 1998:591-600.

[6]汤可宗，吴 隽，赵 嘉. 基于多样性反馈的自适应粒子群优化算法[J]. 计算机应用, 2013,33(12):3372-3374.

[7] Sun S Y， Li J W. A two-swarm cooperative particle swarms optimization [J]. ScienceDirect,2014(15):1-18.

[8] Beard R W， Mdain T W， Goodrich M，et al．Coordinated target assignment and intercept for unmanned air vehicles[J]．IEEE Trans．on Robotics and Automation(to appear),2002,18(6).

UAV Three Dimensional Real-time Route Planning

Xi Jianrui, Yang Jinxiao, Zhang Boliang, Chen Zhixing

(School of Electronics and Information, Northwestern Polytechnical University, Xi′an 710129,China)

UAV path planning is the most important and most complex part of UAV mission planning.Because particle swarm algorithm is easy to fell into local optimal solution and “premature”, and the precision of planning flight route is low, a parallel implementation of two-swarm particle swarm algorithm for route planning is presented, this algorithm is comprised of two particle swarm algorithms which have reverse direction of search, and this algorithm can extend the range of search through cooperation of two particle swarm algorithms, overcome the problem of falling into local optimal solution and improve the precision of flight route. With unexpected threat detected in flight, UAV will search near point of flight route and then replan route from this point to target point.Simulation results show the effectiveness of the algorithm.

UAV; three-dimensional path planning; two-swarm particle swarm optimization; real-time

2015-12-03；

2016-01-07。

席剑锐(1990-)，男，陕西西安人，硕士，主要从事微电子与固体电子学方向的研究。

1671-4598(2016)06-0181-04

10.16526/j.cnki.11-4762/tp.2016.06.050

V279

A