基于VTOL飞行器的滑模控制器设计

王元超，孙 辉

(中国科学院 长春光学精密机械与物理研究所,长春 130033)



基于VTOL飞行器的滑模控制器设计

王元超，孙 辉

(中国科学院 长春光学精密机械与物理研究所,长春 130033)

垂直起降(Vertical takeoff and landing，VTOL)飞行器是具有3个自由度、2个控制输入的非线性欠驱动控制系统，为了解决严重耦合的VTOL欠驱动系统的输出跟踪问题，首先将VTOL动力学模型解耦成一个最小相位系统和一个非最小相位系统，然后分别针对这两个解耦子系统设计滑模控制器，并通过Lyapunov理论证明系统的稳定性，最后仿真结果表明所设计的滑模控制器实现了对轨迹的无稳态误差跟踪，具有较好的鲁棒性，能够为此类欠驱动系统的输出跟踪问题提供设计参考。

垂直起降飞行器；欠驱动；输出跟踪；非最小相位系统；滑模控制；李雅普诺夫稳定

0 引言

垂直起降(Vertical takeoff and landing，VTOL)飞行器对起降地点要求低，能够突破跑道的限制，适用于狭小的空间和复杂的地形环境中使用，可实现飞行器的自由降落，从而具有重要的军用价值和广泛的应用前景[1-2]。

垂直起降飞行器可以弥补固定翼无人机起降应用问题，从而受到越来越多研究者的重视。垂直起降飞行器实际上是一种典型的控制数量少于系统自由度的欠驱动控制系统,此类系统控制输入与系统状态之间存在严重的耦合关系,当系统内部的零动态不稳定时,限制了非线性控制技术的直接应用。文献[3]明确指出对于满足强惯性耦合条件的欠驱动非线性系统可以通过部分反馈线性化的方法来简化系统分析和控制器设计过程。除了部分反馈线性化之外，很难找到一种对一般欠驱动非线性系统普遍适用的控制方法。但是，反馈线性化对模型误差和外界干扰的鲁棒性不强，因而在实际中很难得到真正应用。目前对于欠驱动非线性系统控制的研究往往是针对某一类特定的系统，其中最常见的系统有垂直起降飞行器、柔性机械臂和船舶等。文献[4-5] 利用后推法Backstepping的设计思想，实现了全局轨迹的跟踪控制，但是需要控制模型直接或间接变化为严格反馈形式, 且存在“微分爆炸”现象。文献[6]采用动态面控制策略消除Backstepping设计法存在的“微分爆炸”现象，简化了设计过程，但其稳态跟踪误差不能收敛到零。文献[7]提出一种级联观测器的鲁棒容错控制方案来使得故障系统的输出渐近跟踪给定的期望轨迹。文献[8]引入输入补偿的线性辅助系统，解决了VTOL轨迹跟踪输入饱和的问题。

滑模控制器具有鲁棒性好和全局指数收敛稳定等优点，在飞行器[8-10]和多关节机器人[11]的轨迹控制已经得到了应用。苏善伟等人在文献[12]中详细综述了非线性非最小相位系统的控制研究问题。本文在以上文献的基础上，将VTOL飞行器欠驱动模型解耦成一个最小相位系统和一个非最小相位系统，分别对这两个子系统设计滑模控制器，并通过Lyapunov理论证明了系统的稳定性，能够实现无稳态误差的指数收敛。

1 VTOL飞行器动力学模型

只考虑VTOL飞行器的起降过程，在OXY平面上对飞行器进行受力分析，如图1所示。

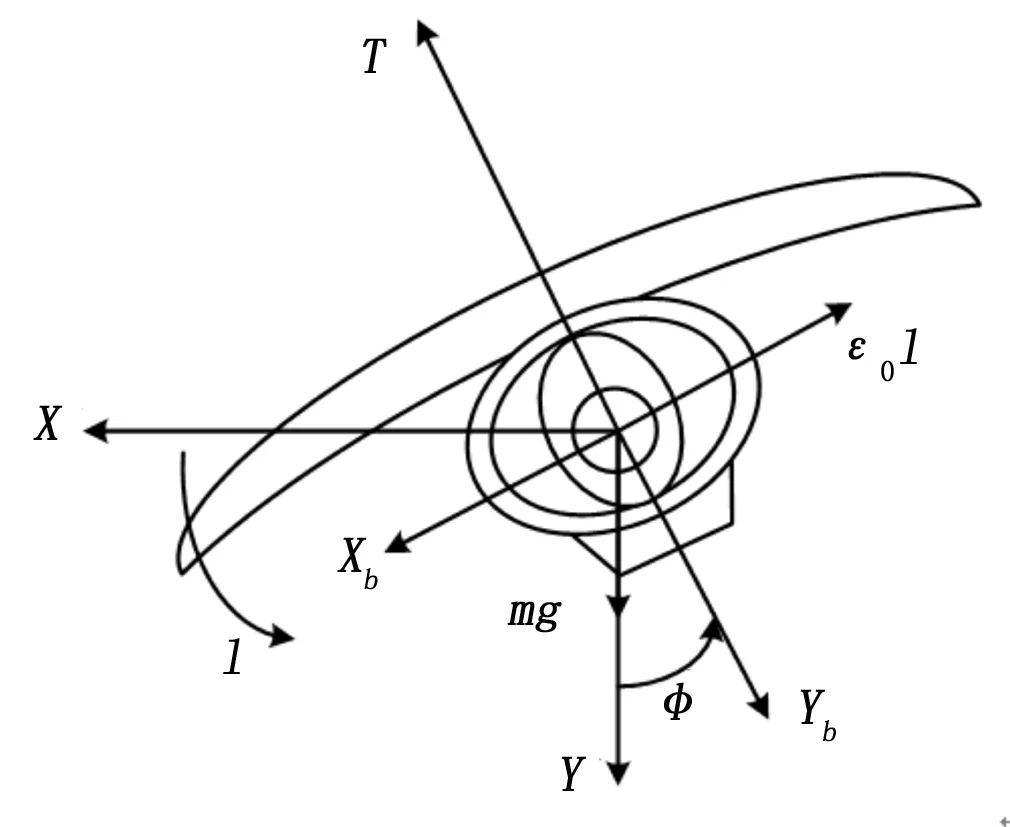
图1 VTOL飞行器受力分析图

根据受力分析图，可以建立VTOL飞行器的动力学模型为：

(1)

其中：m为飞行器的质量，T为飞行器的推力，l为飞行器的滚转力矩，g为重力加速度，Ixx为惯量，ε0表示由滚转力矩产生横侧向位移寄生力一个比例因子。

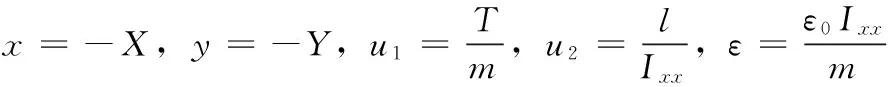
(2)

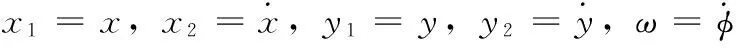
(3)

由式(3)可以看出，VTOL飞行器动力学模型有3个状态输出，分别为飞行器的横纵位置x1(t)、y1(t)和滚转角速度φ(t)，向量形式为y(t)=[x1(t)y1(t)φ(t)]T；以及有与推力T和滚转力矩l相关的两个控制输入u1(t)、u2(t)，向量形式即u(t)=[u1(t)u2(t)]T。

2 模型解耦变换

由式(3)可以看出，VTOL飞行器动力学模型是一个典型的欠驱动控制系统，而且控制输入与系统状态，以及两个输入之间存在严重的耦合关系，这些问题限制了滑模控制的直接应用。 这里为了解决VTOL欠驱动系统的输出跟踪控制问题，将对VTOL飞行器动力学进行解耦。定义飞行器横纵坐标的期望值分别为x1d和y1d，控制目标为飞行器的位置能够跟踪期望指令，并且保证滚转角φ镇定。则系统跟踪误差模型为：

(4)

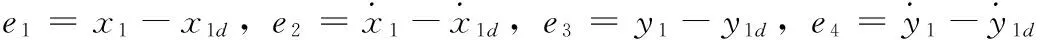
将式(4)中第二个和第4个微分方程写成矩阵形式，可得：

(5)

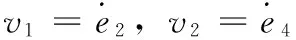
(6)

求出：

(7)

结合式(4)、(6)和(7)可得：

(8)

为了消除中间控制变量v1和v2，引入新的状态变量λ。令：

(9)

考虑式(9)，当e2→0且e4→0时，则λ→εω。因此可以用λ代替ω。

由式(9)可得：

(10)

由式(8～10)可得：

(11)

(12)

VTOL飞行器轨迹跟踪的目标为实现位置的跟踪期望指令x1d和y1d，且滚转角φ镇定。即实现e1→0，e2→0，e3→0，e4→0，φ→0，ω→0。

由式(11～12)可将VTOL飞行器跟踪控制系统写成：

(13)

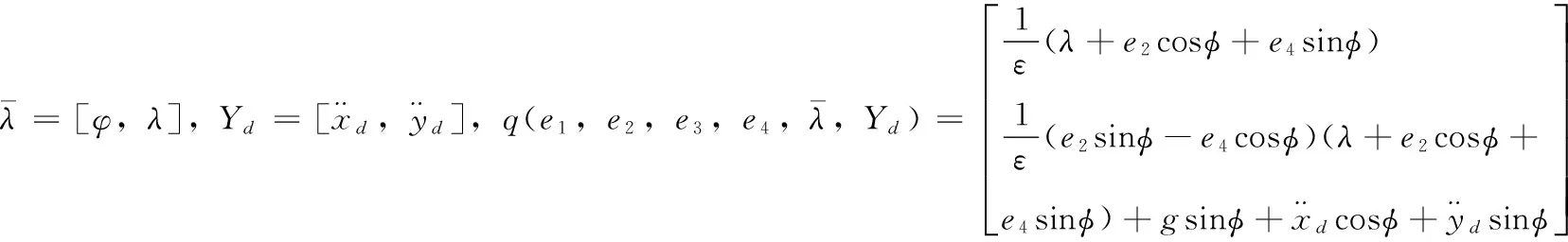
考察系统的零动态：

(14)

(15)

可见，对于式(13)在零动态q(·)与[e1e2]相关，而与[e3e4]不相关。

由以上分析，可以将VTOL飞行器跟踪控制系统解耦成一个垂直方向的动态方程最小相位系统：

(16)

以及一个横侧向与滚转耦合的非最小相位系统：

(17)

3 滑模控制器设计

3.1 最小相位系统的滑模控制器设计

针对式(16)的最小相位系统，选取滑模面函数为：

(18)

设计滑模控制器为：

v2=-ce4-ksign(σ1)

(19)

其中：k>0。

(20)

表明最小相位系统是一致渐近稳定的。

3.2 非最小相位系统的滑模控制器设计

针对式(17)的非最小相位系统，定义δ1=e2，δ2=[e1φλ]，则式(17)可化为：

(21)

其中：

利用泰勒公式将式(21)中第二式写成：

(22)

其中,

(23)

(24)

(25)

取滑模面函数为：

(26)

其中：α=[α1α2α3]，并且使A21α+A22满足Hurwitz判定条件。

由滑模面函数满足σ2=δ1-αδ2=0，可得δ1=αδ2，因此由式(21)和(25)，得：

(27)

由于(A21α+A22)满足Hurwitz判定条件，式(21)表示的系统是一致渐近稳定的。因此，有δ2→0且δ1=αδ2→0，则由定义式δ1=e2，δ2=[e1φ λ]，有e1→0，e2→0，φ→0，ω→0。

设计滑模控制器为：

(28)

其中：ξ>0。

下面证明系统的稳定性，取Lyapunov函数为：

(29)

则：

(30)

表明非最小相位系统是一致渐近稳定的。

(31)

sI-(A21α+A22)的行列式为：

(32)

由劳斯判据得：

(33)

因此，只要α=[α1α2α3]满足式(33)，即可保证非最小相位系统的一致渐近稳定性。

4 仿真分析

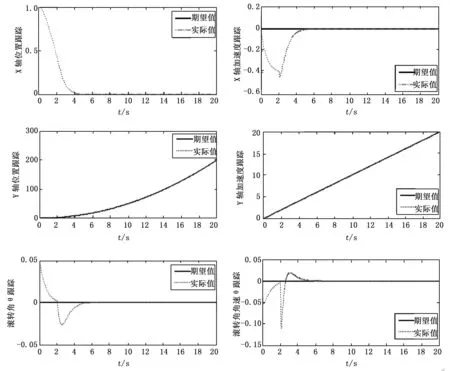
图2 仿真结果图

从图2可以看出，系统在所设计的控制器下能够很好的实现对位置的无稳态误差跟踪，同时能保证滚转角姿态的镇定，且当初始状态存在一定误差的情况下能够快速响应跟踪。

5 结论

本文建立了VTOL飞行器动力学模型，并通过系统模型零动态的分析，将其解耦成一个最小相位系统和一个非最小相位系统，利用理想内模将输出跟踪问题转化为状态跟踪误差，分别对解耦的两个系统分别设计了滑模控制器，利用Lyapunov理论证明了系统的稳定，并且具有一致渐近稳定，同时给出了控制参数的求取过程。最后通过仿真验证了设计的滑模控制器能够实现位置的无稳态误差跟踪控制，具有较强的鲁棒性。

[1] 刘 凯，叶赋晨.垂直起降飞行器的发展动态和趋势分析[J].航空工程进展，2015，6(2)：127-138.

[2] 王冠林，武 哲.垂直起降无人机总体方案分析及控制策略综合研究[J].飞机设计，2006(3)：25-30.

[3] Spong M W. Partial Feedback linearization of underactuated mechanical systems[A]. Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems[C]. Munich, Germany, 1994：314-321.

[4] 刘盛平，陆 震，吴立成.垂直起降飞机的全局轨迹跟踪控制[J].控制与决策，2007，22(8)：899-902.

[5] 贾鹤鸣，王 璐.欠驱动垂直起降UAV的全局K指数轨迹跟踪[J].中南大学学报(自然科学版)，2013，44(8)：3231-3239.

[6] 袁瑞侠，刘金琨.欠驱动VTOL飞行器的位置反馈动态面控制[J].系统工程与电子技术，2014，36(11)：2266-2271.

[7] 蒋元庆，杨 浩，姜 斌.基于级联观测器的垂直起降飞机鲁棒容错控制[J].信息与控制，2015，44(1)：76-82.

[8] 刘金琨，龚海生.有输入饱和的欠驱动VTOL飞行器滑模控制[J].机电与控制学报，2013，17(3)：92-97.

[9] 常 琳，金 光，范国伟.基于terminal滑模控制的小卫星机动方法[J].光学 精密工程，2015，23(2)：485-496.

[10] 李 迪，陈向坚，续志军.增益自适应滑模控制器在微型飞行器飞行姿态控制中的应用[J].光学 精密工程，2013，21(5)：1183-1191.

[11] 邵克勇，马千惠，邹 运，等.基于径向基函数神经网络的多关节机器人滑模控制器[J].计算机测量与控制，2014，22(5)：1385-1387.

[12] 苏善伟，朱 波，向锦武，等.非线性非最小相位系统的控制研究综述[J].自动化学报，2015，41(1)：9-21.

Sliding Mode Controller Design for VTOL Aircraft

Wang Yuanchao，Sun Hui

(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences,Changchun 130033, China)

The Vertical takeoff and landing aircraft is a nonlinear underactuated control system with three degrees of freedom and two control inputs. In order to solve the problem of output tracking of the serious coupling VTOL system, firstly, the VTOL dynamic model is decoupled into a minimum phase system and a nonminimum phase system. And then, the sliding mode controllers are designed respectively for the two decoupling system, meanwhile, the system's stability is proved by Lyapunov function. Finally, the simulation results show that the proposed sliding mode controller can achieve the tracking of the trajectory without steady-state error and has strong robustness. The method proposed in this paper can also provide design reference for the output tracking problem of this kind of underactuated system.

VTOL aircraft; underactuated; output tracking; nonminimum phase system; sliding mode control; Lyapunov stability

2015-12-01；

2015-12-25。

中国科学院三期知识创新工程资助项目(YYYJ-1122) 。

王元超(1986-)，男，湖北武汉人，硕士，助理研究员，主要从事飞行器飞行控制方向的研究。

1671-4598(2016)06-0102-04

10.16526/j.cnki.11-4762/tp.2016.06.028

TP273,TP249

A