一组1553B总线网络可靠性评估模型研究

何 鑫，周 晴，薛长斌

(中国科学院国家空间科学中心，北京 100190)



一组1553B总线网络可靠性评估模型研究

何 鑫，周 晴，薛长斌

(中国科学院国家空间科学中心，北京 100190)

在工程中，数据网络结构往往决定了数据传输的网络可靠性；比如，若干节点的1553B总线可以设计为1个BC和多个RT的单层总线结构，也可以设计为双层BC-RT的总线结构；因此，如何比较这两种设计的网络可靠性高低成为关键问题；为了解决这一问题，文中以上述总线结构设计问题为切入点，结合容斥原理和总线网络结构的特点，提出一组网络可靠性评估模型，并通过这组模型对单层和双层1553B总线结构的网络可靠性进行评估、比较和分析，为工程中网络可靠性评估模型的选择和使用提供指导，为总线网络结构设计合理性的定量分析提供数据支撑，同时为网络可靠性设计要求的满足提供理论依据；最后，文中对总线设计网络可靠性问题研究的发展趋势进行讨论。

网络可靠性；总线结构；评估模型

0 引言

随着计算机科学的不断发展，计算机网络覆盖的领域不断拓展，现已成为人们生产和生活的重要组成部分。然而，在使用中网络失效的问题却时有发生。因此，网络可靠性问题逐渐成为了人们关注的焦点。

网络可靠性是指网络在规定时间和规定条件下完成规定功能的能力[1]。在工程中，数据网络拓扑结构往往决定了数据传输的网络可靠性。比如，若干节点的1553B总线可以设计为1个BC和多个RT的单层拓扑结构，也可以设计为双层BC-RT的拓扑结构。因此，如何比较这两种设计的网络可靠性高低成为关键问题。

为了比较网络可靠性的高低，合理安排网络的拓扑结构，保证网络可靠性满足设计要求，需要通过网络可靠性评估的手段进行评判。然而，由于评估模型多种多样，计算复杂度也千差万别，造成解决实际工程问题时评估模型的选择和使用成为了一个难题。

为了解决这一难题，文中以上述总线拓扑结构设计问题为切入点，结合容斥原理和总线网络拓扑结构的特点，提出一组网络可靠性评估模型，并通过这组模型对单层和双层1553B总线结构的网络可靠性进行评估、比较和分析，为工程中网络可靠性评估模型的选择和使用提供指导，为网络拓扑结构设计合理性的定量分析提供数据支撑，同时为网络可靠性设计要求的满足提供理论依据。最后，文中对总线设计网络可靠性问题研究的发展趋势进行讨论。

1 模型

在历史上，网络可靠性研究领域曾出现过一些经典算法，如：状态枚举法[2]、容斥原理方法[3]、不交积和法[4]和因子分解法[5]等。近年来，在国内外的网络可靠性研究中，新的评估方法层出不穷[6-7]，出现了基于不交积和的算法[8]、基于状态枚举的算法[9]、递归截断算法[10]、仿真法[11]、智能算法[12]等方法。但这些方法在使用时会遇到假设条件不易满足、计算量复杂等困难。

因此，为了有效的比较单层和双层1553B总线结构的网络可靠性，文中在评估模型的选择上采用了一组从简单到复杂的模型，逐步深入的评估、比较和分析，既考虑计算量的简化，又考虑尽量客观完善的描述问题。下面详细描述这一组网络可靠性评估模型。

1.1 模型1

考虑到总线中的各节点的故障将直接影响整个网络的可靠性，同时为了尽量简少计算量，因此，模型1采用如下假定条件：

1)网络中各节点只有正常、故障两种状态，且正常的概率均为p(p∈[0,1])。

2)网络中各节点正常、故障的概率是相互独立的。

3)网络中各总线只有正常一种状态。

根据模型1的假定条件，对由5个节点组成的网络进行建模，得到模型1的双层和单层网络拓扑结构如图1所示。

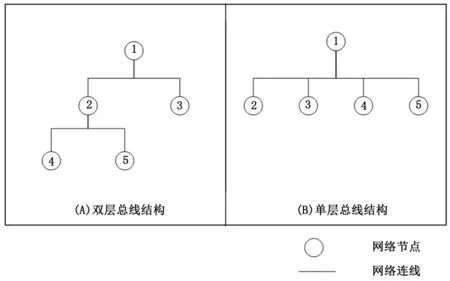
图1 模型1的5节点双层和单层网络模型

设Ai为第i个最小路集，i=1,2,…,n，AI表示指标集为I的交集，k为集合I的元素个数，运用容斥原理计算网络正常的概率公式为：

(1)

依据容斥原理公式(1)，模型1的双层和单层网络拓扑结构正常的概率分别为：

P(A1)=p5-3p4+2p3+p2

P(B1)=-p5+4p4-6p3+4p2

1.2 模型2

模型1假定了网络中各总线只有正常一种状态，但在实际应用中很可能遇到总线故障的情况，因此，为了更完善的反映真实的网络拓扑结构特点，模型2考虑增加总线故障的假定条件。

模型2采用如下假定条件：

1)网络中各节点、各总线只有正常、故障两种状态，且正常的概率均为p(p∈[0,1])。

2)网络中各节点、各总线正常、故障的概率是相互独立的。

根据模型2的假定条件，对5个节点组成的网络进行建模，得到模型2的双层和单层网络拓扑结构如图4所示。图中“(A)双层总线结构”的节点1、3、4、6、7和“(B)单层总线结构”的节点1、3、4、5、6为网络中的节点，“(A)双层总线结构”的节点2、5和“(B)单层总线结构”的节点2为网络中的总线。

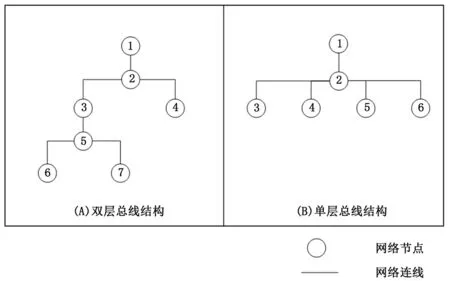
图2 模型2的5节点双层和单层网络模型

依据容斥原理公式(1)，模型2的双层和单层网络拓扑结构正常的概率分别为：

P(A2)=p7-3p6+2p5+p3

P(B2)=-p6+4p5-6p4+4p3

1.3 模型3

模型2假定了各节点和各总线均存在故障状态，但在实际情况中，网络中的某些关键节点还有可能存在主备份的情况，因此，为了进一步客观全面的表达网络拓扑结构特点，模型3考虑增加双备份的假定条件。

模型3采用如下假定条件：

1)网络中各节点、各总线只有正常、故障两种状态。

2)网络中各节点、各总线正常、故障的概率是相互独立的。

3)网络中各个作为BC的节点、各总线采用双备份，这些双备份点正常的概率均为1-(1-p)2(p∈[0,1])，其他节点正常的概率均为p(p∈[0,1])。

根据模型3的假定条件，对5个节点组成的网络进行建模，得到模型3的双层和单层网络拓扑结构如下图所示。图中“(A)双层总线结构”的节点1、3、4、6、7和“(B)单层总线结构”的节点1、3、4、5、6为网络中的节点，“(A)双层总线结构”的节点2、5和“(B)单层总线结构”的节点2为网络中的总线。同时，图中“(A)双层总线结构”的节点1、2、3、5和“(B)单层总线结构”的节点1、2为双备份点，其余为单备份点。

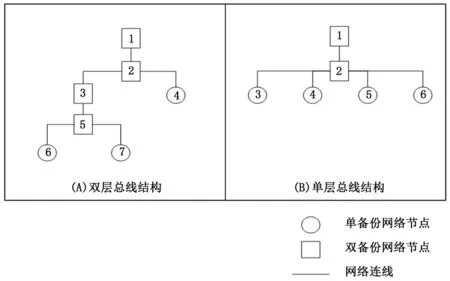
图3 模型3的5节点双层和单层网络模型

依据容斥原理公式(1)，模型3的双层和单层网络拓扑结构正常的概率分别为：

经过因式分解，可得：

综上所述，本章建立了一组网络可靠性评估模型，得到了3个模型下双层和单层总线正常的概率。下一章将依据这3个模型，对双层和单层两种总线拓扑结构的网络可靠性进行进一步的比较和分析。

2 对比和分析

上一章根据建立的3个模型，分别求出双层和单层1553B总线网络拓扑结构正常的概率表达式。本章采取作差判断是否大于0的方法，分别在这3个模型下对双层和单层1553B总线网络拓扑结构的网络可靠性进行比较和分析。

2.1 在模型1条件下对网络可靠性的对比和分析

在模型1条件下，通过作差的方法比较P(A1)与P(B1)的大小：

经过分析可知：因为p∈[0,1]，所以2p-3<0，且(p-1)2p2≥0，因此ΔP1≤0。

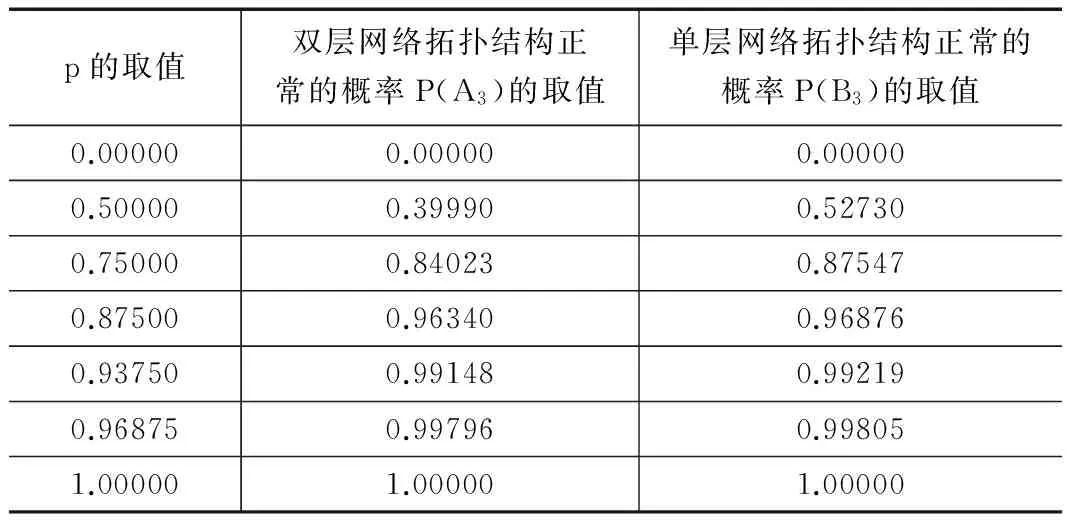
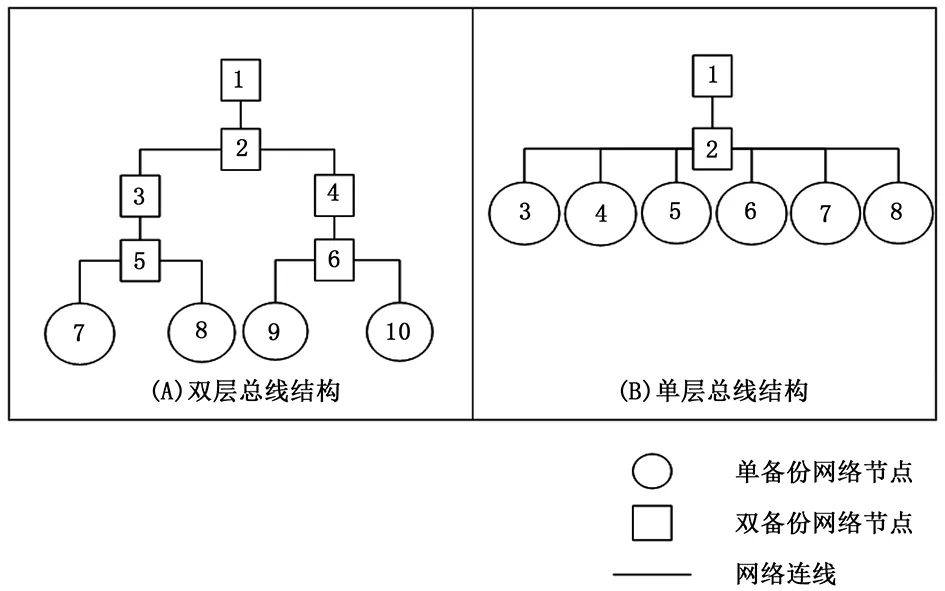
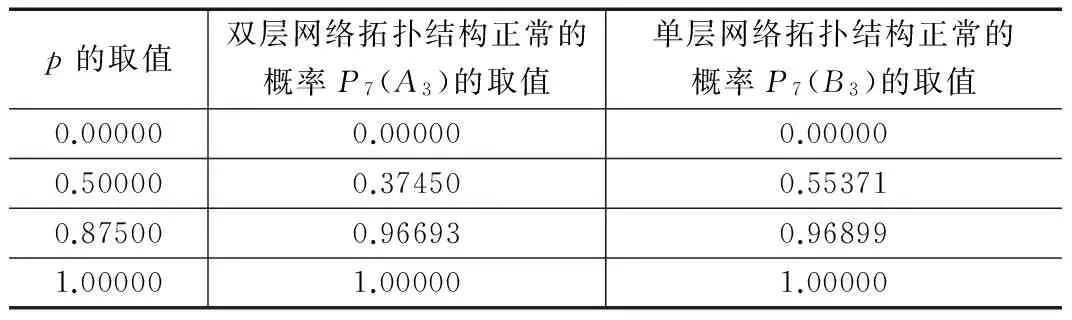
由此可见，在模型1的条件下，双层网络拓扑结构的网络可靠性小于等于单层网络拓扑结构。其中，在p=0或p=1时，双层网络拓扑结构的网络可靠性等于单层网络拓扑结构；在0

2.2 在模型2条件下对网络可靠性的对比和分析

在模型2的条件下，通过作差的方法比较P(A2)与P(B2)的大小：

经过分析可知：因为p∈[0,1]，所以p3-3<0，且(p-1)2p2≥0，因此ΔP2≤0。

由此可见，在模型2的条件下，双层网络拓扑结构的网络可靠性小于等于单层网络拓扑结构。其中，在p=0或p=1时，双层网络拓扑结构的网络可靠性等于单层网络拓扑结构；在0

2.3 在模型3条件下对网络可靠性的对比和分析

在模型3的条件下，通过作差的方法比较P(A3)与P(B3)的大小：

经过分析可知：因为p∈[0,1]，所以(p-1)3≤0，且-3p≤0，p-2≤-1，得到(p-1)3-3p+1≤1，且3(p-2)≤-3，进而(p-1)2[(p-1)3-3p+1]≤1，可得{(p-1)2[(p-1)3-3p+1]+ 3(p-2)}≤-2，因此ΔP3≤0。

由此可见，在模型3的条件下，双层网络拓扑结构的网络可靠性小于等于单层网络拓扑结构。其中，在p=0或p=1时，双层网络拓扑结构的网络可靠性等于单层网络拓扑结构；在0

3 讨论

通过上述两章的建模、评估、比较和分析过程，文中得出了双层和单层1553B网络正常的概率大小。下面对各模型的计算结果进行讨论。

3.1 对各模型计算结果的小结

通过上一章的对比和分析，可以发现：无论选择上述3个模型中的任意一个模型，双层网络拓扑结构的网络可靠性均小于等于单层网络拓扑结构。其中，在p=0或p=1时，双层网络拓扑结构的网络可靠性等于单层网络拓扑结构；在0

3.2 单双层正常概率之差的变化趋势分析

通过对上述各模型计算结果的分析，可以比较出双层和单层网络正常的概率大小。于此同时，在相同的模型下，双层和单层网络正常的概率之差是否存在一定的规律？下面以模型3为例，对此进行分析。

在p的取值为0.00000、0.50000、0.75000、0.87500、0.93750、0.96875、1.00000时，根据模型3的假定条件可得含5个节点条件下双层和单层拓扑结构正常的概率P(A3)和P(B3)的取值结果，如表1所示。

表1 含5个节点时双层和单层网络正常的概率随p变化趋势表

由此可见，随着p的增加，P(A3)和P(B3)的差距将逐渐缩小。当p为0.96875时，P(A3) 和P(B3)几乎相等；当p为0.00000、1.00000时，P(A3) 和P(B3)完全相等。

3.3 节点增加的情况分析

通过对上述各模型计算结果的分析，可以在5个节点的情况下，比较出双层和单层网络正常的概率大小。为了更有说服力，下面以模型3为例，在7个节点的情况下，比较双层和单层网络正常的概率结果。

根据模型3的假定条件，对7个节点组成的网络进行建模，得到模型3的双层和单层网络拓扑结构如图4所示。图中“(A)双层总线结构”的节点1、3、4、7、8、9、10和“(B)单层总线结构”的节点1、3、4、5、6、7、8为网络中的节点，“(A)双层总线结构”的节点2、5、6和“(B)单层总线结构”的节点2为网络中的总线。同时，图中“(A)双层总线结构”的节点1、2、3、4、5、6和“(B)单层总线结构”的节点1、2为双备份点，其余为单备份点。

图4 模型3的7节点双层和单层网络模型

依据容斥原理公式(1)，运用模型3对图4的网络可靠性进行评估，得出双层和单层网络拓扑结构正常的概率分别为：

P7(B3)=6(-p2+2p)2p-15(-p2+2p)2p2+

20(-p2+2p)2p3-15(-p2+2p)2p4+6(-p2+2p)2p5-

(-p2+2p)2p6

在p的取值为0.00000、0.50000、0.87500、1.00000时，根据模型3的假定条件可得含7个节点条件下双层和单层拓扑结构正常的概率P7(A3)和P7(B3)的取值结果，如表2所示。

表2 含7个节点时双层和单层网络正常的概率随p变化趋势表

由此可见，无论p(p∈[0,1])取值如何，含7个节点时双层网络正常的概率小于等于单层网络正常的概率。

3.4 对模型3的调整和分析

在模型3中，将单备份点正常的概率设为p，双备份点正常的概率设为1-(1-p)2，因此双备份点与单备份点正常的概率相互不独立。为了进一步分析模型3中双层和单层网络拓扑结构的网络可靠性大小，对模型3进行调整，提出模型4。

模型4采用如下假定条件：

1)网络中各节点、各总线只有正常、故障两种状态。

2)网络中各节点、各总线正常、故障的概率是相互独立的。

3)网络中各个作为BC的节点、各总线采用双备份，这些双备份点正常的概率均为p1(p1∈[0,1])，其他节点正常的概率均为p2(p2∈[0,1])，且p1与p2相互独立。

依据容斥原理公式(1)，运用模型4对图3的网络可靠性进行评估，得出双层和单层网络拓扑结构正常的概率分别为：

P(A4)=p14(p23-3p22+2p2)+ p12p2

P(B4)=p12(-p24+4p23-6p22+4p2)

在模型4的条件下，通过作差的方法比较P(A4)与P(B4)的大小：

因为p1∈[0,1]，p2∈[0,1]，所以p2-1≤0，p2≤0，因此p14p2(p2-1)(p2-2)≤0。为了判断p2(p2-2)2+2(p2-2)+1是否小于等于0，选取一组值进行分析：

当p2=0.00000时，p2(p2-2)2+2(p2-2)+1=-3.00000≤0。

当p2=0.12500时，p2(p2-2)2+2(p2-2)+1=-2.31055≤0。

当p2=0.50000时，p2(p2-2)2+2(p2-2)+1=-0.87500≤0。

当p2=0.87500时，p2(p2-2)2+2(p2-2)+1=-0.14258≤0。

当p2=0.93750时，p2(p2-2)2+2(p2-2)+1=-0.06665≤0。

当p2=1.00000时，p2(p2-2)2+2(p2-2)+1=0.00000≤0。

因此，断言[p2(p2-2)2+2(p2-2)+1]≤0，但是仍需要在数学上严格证明。由此可知，在断言成立的前提下，p12p2[p2(p2-2)2+2(p2-2)+1]≤0，即ΔP4≤0。

4 结论

为了比较单层和双层1553B总线结构的网络可靠性，文中结合容斥原理和总线网络拓扑结构的特点，提出一组网络可靠性模型，并通过这组模型对单层和双层总线结构的网络可靠性进行评估、比较和分析。通过分析和讨论可知，在文中的各种模型假定条件下，双层1553B总线网络拓扑结构的网络可靠性均小于等于单层1553B总线网络拓扑结构。

文中的建模、评估、比较和分析结果，可以为工程中网络可靠性评估模型的选择和使用提供指导，为网络拓扑结构设计合理性的定量分析提供数据支撑，同时为网络可靠性设计要求的满足提供理论依据。

然而，在工程中，双层1553B总线网络结构的使用范围广泛，也具有较高的网络可靠性。而且，工程中情况复杂，并不一定满足文中的全部假定条件。因此，不能仅仅通过文中的论述就简单的认为单层1553B总线网络结构优于双层1553B总线网络结构。这种总线设计的网络可靠性问题仍将在未来得到进一步的研究和应用。

[1] 黄 宁,伍志韬. 网络可靠性评估模型与算法综述[J]. 系统工程与电子技术， 2013 35(12):2651-2660.

[2] Moore E. F., Shannon C. E. Reliable Circuits Using Less Reliable Relays[J]. Journal of the Franklin Institute. 1956，262(3): 191-208.

[3] Lin P M, Leon B J, Huang T C. A New Algorithm for Symbolic System Reliability Analysis[J]. IEEE Transactions on Reliability. 1976，R-25(1):2-15.

[4] Fratta L, Montanari U. A Boolean Algebra Method for Computing the Terminal Reliability in a Communication Network[J]. IEEE Transactions on Circuit Theory. 1973，20(3):203-211.

[5] Moskowitz F. The Analysis of Redundancy Networks[J]. Transactions of American Institute of Electrical Engineers. Part 1: Communication and Electronics. 1958，77(5):627-632.

[6] 江逸楠,李瑞莹,黄 宁,等. 网络可靠性评估方法综述[J]. 计算机科学, 2012,39(5):9-13.

[7] 杨孝平,尹春华. 复杂网络可靠性评价指标[J]. 北京信息科技大学学报,2010,25(3):92-96.

[8] Mishra R, Chaturvedi S K. A Cutsets-based Unified Framework to Evaluate Network Reliability Measures [J]. IEEE Transaction on Reliability. 2009，58(4):658-666.

[9] Sahinoglu M, Ramamoorthy C V, Smith A E. A Reliability Block Diagramming Tool to Describe Networks[A]. Annual Reliability and Maintainability Symposium[C]. 2014:141-145.

[10] Sharafat A R, Ma’rouzi O R. All-terminal Network Reliability Using Recursive Truncation Algorithm[J]. IEEE Transactions on Reliability. 2009,58(2):338-347.

[11] Yeh W C. A Squeeze Response Surface Methodology for Finding Symbolic Network Reliability Functions[J]. IEEE Transactions on Reliability. 2009,58(2):374-382.

[12] 罗景峰、刘艳秋. 智能算法在全终端网络可靠性优化设计中的应用[J]. 计算机测量与控制,2007(6):782-785.

Research on a Group of 1553B Bus Network Reliability Evaluation Models

He Xin, Zhou Qing, Xue Changbin

(National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China)

In engineering, network reliability of data communication is often determined by data network structure. For instance, 1553B bus with some nodes could be designed into a one-layer bus structure with a BC node and some RT nodes. It also could be designed into a two-layer BC-RT bus structure. Therefore, it is a crucial question that how could these two kinds of design be compared for network reliability. In order to solve this problem, this paper makes this problem of bus structure design as a breakthrough point, combines principle of inclusion-exclusion and bus structure characteristics, and provides a group of network reliability evaluation models which could be used to evaluate, compare and analyze network reliability of one-layer and two-layer 1553B bus structure. This paper could guide to choose and use network reliability evaluation models in engineering, give quantitative data support to reasonable data network structure design, and provide theoretical proof to satisfaction of network reliability design requirements. At last, the developing trends of bus design network reliability research will be discussed.

network reliability; bus structure; evaluation model

2016-03-18；

2016-05-05。

何 鑫(1983-) 男，北京人，硕士，工程师,主要从事软件工程技术、软件安全性与可靠性技术方向的研究。

1671-4598(2016)09-0292-04

10.16526/j.cnki.11-4762/tp.2016.09.082

TP311

A